螺栓球柱节点单向受弯性能有限元分析

2020-02-27郭小农曾强黄泽韡彭礼陈宇

湖南大学学报（自然科学版） 2020年1期

郭小农，曾强，黄泽韡，彭礼，陈宇

（1. 同济大学土木工程学院，上海200092；2. 上海泰大建筑科技有限公司，上海200092）

我国现行规范《空间网格结构技术规程》（JGJ7—2010）[1]规定：对于网架结构和双层网壳结构，可采用空间铰接杆系结构进行分析，节点假定为铰接；对于单层网壳结构，可采用空间刚接梁系结构进行分析，节点假定为刚接.但现有研究表明，大多数空间网格结构的节点实际上是半刚性节点，且节点刚度对结构的力学性能有很大影响.王星、完海鹰等[2-4]通过数值分析计算，回归得出了焊接球节点弯曲刚度的计算式，并在网架分析过程中考虑了节点刚度的影响，结果表明网架内力受节点刚度影响较小而挠度受节点刚度影响较大.Lopez 等[5-6]、张竟乐等[7]、康菊等[8]通过试验研究和有限元模拟，分析了不同节点刚度对单层网壳稳定性的影响，研究发现节点刚度对结构的整体稳定性有较大影响.因此，对空间网格结构的节点刚度及其对结构性能影响的研究具有重要意义.

螺栓球柱节点是彭礼等[9]提出的一种适用于无檩网架结构的新型节点.典型的螺栓球柱节点由空心圆柱筒体和实心螺栓半球两部分等强焊接而成，必要时可在筒体开口处增设环形加劲肋，以提高节点的刚度及承载力.对于采用该节点的无檩网架，上弦杆可采用矩形管截面，并通过弧形端板、高强螺栓、弧形垫片等部件与节点体紧密连接；腹杆可采用圆管截面，并与实心半球连接.由于上弦杆为矩形管，抗弯刚度较大，因此结构无需再设置支托和檩条，而将屋面板直接支承于上弦杆表面，具有节约材料、方便施工的优点，并可获得良好的建筑效果.

与传统网架节点相比，对螺栓球柱节点受力性能的研究相对较少.目前仅郭小农等[10-11]对螺栓球柱节点的受压、受拉及受弯性能进行了试验研究，初步得到了节点在不同受力状态下的破坏模式、应力分布规律及承载力特征；随后通过数值模拟详细分析了单向受压节点的力学特性，提出了螺栓球柱节点单向受压承载力的计算式.然而，螺栓球柱节点是半刚性节点，在轴向受力时会存在荷载偏心现象，使节点承受较大的次弯矩.上述研究主要针对螺栓球柱节点的轴向受力性能进行，缺乏对节点受弯性能的深入研究.

本文在文献[10]中节点受弯试验的基础上，建立了单向受弯螺栓球柱节点的数值分析模型，并将数值分析结果与试验结果进行对比，验证了数值模型的可靠性.随后对受弯节点模型进行了合理简化，并对影响螺栓球柱节点受弯性能的因素进行了详细的参数分析，得到了节点抗弯刚度的主要影响因素.

1 试验简介

1.1 试件设置及材料性能

郭小农等[10]共进行了2 个足尺单向受弯节点的静力试验.试件详图如图1 所示，具体几何尺寸见表1.每个球柱节点均与4 根矩形钢管连接，杆件截面规格均为120×60×5（单位为mm），相邻杆件夹角为90°.为方便加载，各杆件端部均焊接矩形端板，并在实心半球上焊接圆管及正方形端板.杆件及节点的材料牌号均为Q235B，焊缝采用E43 焊条等强焊接，所有螺栓均采用10.9 级的M20 螺栓.

图1 试件详图Fig.1 Configurations of the specimen

杆件及节点的材料性能由拉伸试验测定，试验前从圆柱体的芯部取样制作了6 个材料拉伸试样，最终得到试件节点区材料的力学性能平均值为：弹性模量E=2.095×105MPa，屈服强度fy=215.67 MPa，抗拉强度fu=449.73 MPa，断后伸长率δ5=31.13%，最大荷载下总延伸率Agt=19.40%.

表1 螺栓球柱节点试件几何尺寸Tab.1 Dimensions of BBC joint specimens

1.2 加载方式及测点布置

螺栓球柱节点用于无檩网架上弦，主要承受压力.研究发现螺栓球柱节点是一种半刚性节点，承载变形后轴力可能发生偏心，产生不可忽略的次弯矩.因此对节点施加单向弯矩，以研究节点的受弯性能.加载方式见图2（a），在实心半球上焊接圆管及加载板以便于施加荷载，弯矩通过作用在加载板上的荷载产生.测点布置见图2（b），节点的竖向挠度值可由位移计D1～D4的读数按式（1）计算得出.

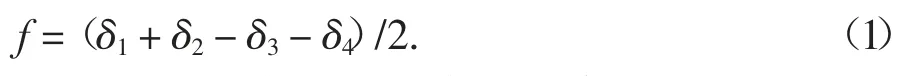
式中：f 为单向受弯节点的中心挠度，mm；δ1～δ4为位移计D1～D4的读数，mm.

图2 加载方式及测点布置Fig.2 Loading scheme and measurement arrangement

1.3 试验结果及分析

试验完成后拆卸试件进行观察，试件的破坏模式和极限荷载见表2.试件的主要破坏模式为螺栓拔出破坏.对于无肋试件JD1，圆柱筒壁在管口处沿受力方向明显扩张，在垂直受力方向收缩，而在靠近半球处变形较小；受弯杆靠近管口侧的螺栓发生拔出，弧形端板与筒壁明显脱开，靠近半球侧的筒壁则有受杆件挤压留下的凹痕.对于带肋试件JD2，破坏时圆柱筒壁未见明显变形，节点刚度和承载力显著提高，除发生螺栓拔出外，受力杆与弧形端板间的焊缝发生撕裂.

表2 试验结果汇总Tab.2 Test results

2 数值模型的建立

2.1 模型几何尺寸及构造

采用有限元软件ABAQUS 建立了节点的数值分析模型.模型的几何尺寸和构造细节均与试件相同.基于试件几何构造、荷载情况及边界条件的对称性，采用1/4 模型模拟受弯试件，并设置对称边界条件.为模拟试验中试件的实际边界条件，在数值模型中建立了加载垫板，数值分析模型如图3（a）所示.

图3 螺栓球柱节点有限元模型Fig.3 FE models of bolted ball-cylinder joint

2.2 接触关系设置

数值分析模型的接触对设置见表3.为模拟螺栓拔出破坏，螺栓杆与弧形端板螺栓孔的接触对设置为表面与表面接触，并在过盈量设置中选择“计算单线螺栓”，线半角设置为30°，螺距设置为1.5 mm.受力杆矩形端板与加载垫板的接触面法向设置为硬接触，切向设置为罚摩擦，摩擦因数取0.2，如图4（a）所示.需要说明的是，为避免施加螺栓预紧力时矩形端板与加载垫板的接触面上产生不应存在的摩擦力，该接触对在施加完螺栓预紧力后激活，这与试件的实际装配过程相符.圆管与实心半球及加载端板的接触面均设置为绑定，以模拟等强焊接，如图4（b）（c）所示.

表3 数值分析模型接触对设置Tab.3 Setting of contact pairs of FE models

图4 数值分析模型接触对设置Fig.4 Setting of contact pairs of FE models

2.3 网格划分

由于数值模型中接触对数量较多，且接触面多为圆弧面，因此计算结果对网格划分比较敏感.对于三维实体，使用结构化网格划分技术或扫掠网格划分技术得到的六面体网格精度较高.通过对比分析，采用非协调单元C3D8I 建立数值模型，可克服剪切自锁问题，并获得精确的计算结果.数值分析模型的网格划分如图3（b）所示.

2.4 荷载施加与分析步建立

数值分析模型采用位移加载，加载面设置在加载端板上，如图4（a）所示.共设置6 个分析步，具体操作如下.

Step1：设置临时约束固定节点、弧形垫片与杆件，同时施加10 N 的螺栓预紧力；

Step2：保持螺栓预紧力不变，释放临时约束；

Step3：将螺栓预紧力调整为10 000 N；

Step4：将螺栓预紧力由“施加螺栓荷载”改为“固定在当前长度”；

Step5：激活加载垫板与受弯杆矩形端板间的接触；

Step6：施加位移荷载.

3 数值分析与试验结果的对比

3.1 破坏模式对比

数值分析模型的破坏模式如图5 和图6 所示，可以发现数值分析结果与试验结果吻合良好.无肋模型JD1 较好地模拟出了管口处筒壁的受拉扩张及弧形端板与筒壁的脱开现象；由于受到弧形端板边缘的挤压，靠近实心半球侧的筒壁出现了明显的应力集中现象，如图5 所示.带肋模型JD2 的刚度较大，筒壁变形相对较小，如图6 所示.此外，受力杆与弧形端板连接处有应力集中现象，与试验中焊缝开裂相吻合.

图5 JD1 试验及数值分析所得的破坏模式Fig.5 Failure modes of tested specimen JD1 and its FE model

图6 JD2 试验及数值分析所得的破坏模式Fig.6 Failure modes of tested specimen JD2 and its FE model

3.2 螺栓内力对比

节点受弯时，管口侧杆件拉力通过弧形端板传至螺栓，再由螺栓经垫片传至节点筒壁，因此螺栓是主要受力部件之一.虽然试验中未测得螺栓内力的具体数值，但螺栓内力的变化可在数值模型中进行验证.

以JD1 为例，受力侧2 颗螺栓的螺栓内力-分析步时间曲线如图7 所示.在第1、2 步平稳建立各接触关系，螺栓内力几乎维持为零；在第3 步施加螺栓预拉力，螺栓内力随时间线性增加至预设值；在第4、5 步固定螺栓长度，并激活加载垫板与矩形端板之间的接触，螺栓内力维持不变；在第6 步施加位移荷载，螺栓内力逐渐增加.由于弧形端板以靠近半球侧边缘为支点旋转，管口侧螺栓距离旋转中心的距离更远，故其内力与变形大于实心半球侧螺栓，如图7和图8 所示.

图7 螺栓内力-分析步时间曲线Fig.7 Internal force of the bolts-step time curves

图8 螺栓最终变形情况Fig.8 Final deformation of the bolts

3.3 荷载-中点挠度曲线对比

图9 对比了螺栓球柱节点试验和数值分析的荷载-中点挠度曲线.通过对比发现，数值分析得到的荷载-中点挠度曲线与试验曲线吻合良好.试件JD2的两条曲线几乎重合，如图9（b）所示；试件JD1 的数值曲线虽然在加载后期偏低，但误差仍在可接受范围内，且数值曲线和试验曲线在弹性阶段和刚进入塑性阶段几乎重合，如图9（a）所示.

图9 荷载-位移曲线对比Fig.9 Comparisons on load-displacement curves

4 数值模型简化及受力分析

4.1 受弯节点数值模型简化

根据螺栓球柱节点轴向受力性能可知[11]，杆件受轴力时，荷载存在偏心现象，节点中将产生较大的次弯矩，刚度矩阵存在耦合项.为消除轴力对节点刚度的影响，确定螺栓球柱节点受弯性能的影响参数，在进行详细的参数分析前，对数值模型进行了简化.

简化后的数值模型如图10（a）所示，将原模型中的杆件、实心半球处的圆管及相应的端板删去，仅保留球柱节点、高强螺栓、弧形垫片及弧形端板，并保持各接触关系不变.同时建立参考点，将弧形端板外侧面上各结点的自由度与参考点耦合，如图10（b）所示.在参考点上设置转角位移荷载进行加载，如图10（c）所示.

图10 螺栓球柱节点简化数值模型Fig.10 Simplified FE model of the BBC joint

4.2 正、负弯矩作用下节点受力分析

螺栓球柱节点单向受压和单向受拉时产生的次弯矩方向相反，可定义节点单向受压时产生的次弯矩为正，单向受拉时产生的次弯矩为负，如图11 所示.选取典型节点模型LZ120-90-10（具体尺寸见表4），分别施加正、负弯矩，得到了节点最终变形情况及受力侧螺栓内力-分析步时间曲线，如图12 和图13 所示.

图11 节点受力简图Fig.11 Force diagram of the joint

由图12（a）可知，在正弯矩作用下，弧形端板绕两颗螺栓连线的中点旋转，管口侧螺栓受压，螺栓内力随荷载增加而下降；半球侧螺栓受拉，螺栓内力随荷载增加而上升，如图13（a）所示.由图12（b）可知，在负弯矩作用下，弧形端板绕靠近半球侧边缘旋转，两颗螺栓均受拉，螺栓内力随荷载增加而上升，且管口侧螺栓内力大于半球侧螺栓内力，如图13（b）所示.

图12 节点最终变形Fig.12 Final deformation of the joint

图13 LZ120-90-10 中螺栓内力-分析步时间曲线Fig.13 Internal force of the bolts-step time curves for LZ120-90-10

节点在正、负弯矩作用下的弯曲-转角曲线如图14 所示.正、负弯矩作用下节点的初始抗弯刚度几乎相同；随着荷载增加，节点抗弯刚度均明显下降，且正弯矩作用下节点的抗弯刚度下降幅度更大.节点受正弯矩作用时，管口处筒壁受压变形，节点的抗弯刚度由圆柱筒壁的刚度控制，材料进入塑性后节点的刚度将很快下降至接近于零；节点受负弯矩作用时，实心半球对筒壁变形有约束作用，节点的抗弯刚度由高强螺栓控制，在材料进入塑性后仍具有一定的刚度.由于在正、负弯矩作用下节点受力性能存在较大差别，因此在参数分析中考虑了正、负弯矩两种情况.

4.3 节点抗弯承载力取值准则

由图14 可知，螺栓球柱节点在正、负弯矩作用下的破坏模式均为延性破坏，且由于材料的强化作用，弯矩-转角曲线无明显下降段.根据欧洲规范[12]中对节点刚度分类的相关规定，螺栓球柱节点属于半刚性节点，因此规定当节点刚度退化至规范规定的半刚性节点刚度范围的下限值时，所对应的弯矩值为节点的抗弯承载力，如图14 所示.其中，Sini，p和Mu，p分别为节点在正弯矩作用下的初始刚度和抗弯承载能力；Sini，n和Mu，n分别为节点在负弯矩作用下的初始刚度和抗弯承载力；Spinned为欧洲规范规定的半刚性节点刚度范围的下限值，Spinned=0.5EIb/Lb，EIb/Lb为节点连接杆件的线刚度，杆件长度Lb取15 倍截面高度.

图14 正、负弯矩作用下节点弯矩-转角曲线对比Fig.14 Comparison on the moment-rotation curves of joints under positive and negative bending moments

5 节点受弯性能影响参数分析

为确定各项参数对螺栓球柱节点受弯性能的影响，建立了46 个受弯节点数值模型，并对每个模型分别施加正、负弯矩.所有螺栓球柱节点数值模型的具体尺寸及正、负弯矩作用下节点的初始抗弯刚度见表4.螺栓球柱节点试件编号为LZ D-h-t，其中LZ表示螺栓球柱节点，D、h、t 分别为螺栓球柱节点的外径、筒壁高度及壁厚，单位为mm.同时，表4 给出了建议的最小矩形管尺寸及配套螺栓尺寸.

表4 数值模型几何尺寸及承载性能Tab.4 Dimensions and bearing capacity of FE models for parametric studies

续表4：

5.1 圆柱筒壁直径的影响

1～4 号模型的弯矩-转角曲线如图15 所示.由图15 和表4 可知，随着圆柱筒壁直径增加，节点的抗弯刚度下降.筒壁直径从100 mm 增长至160 mm时，正、负弯矩作用下节点的初始抗弯刚度分别下降了44.0%和40.8%；抗弯承载力分别下降了21.8%和13.2%.但当筒壁直径D 大于120 mm 时，筒壁直径对节点抗弯刚度及承载力的影响减小.

5.2 圆柱筒壁高度的影响

5～11 号模型的弯矩-转角曲线如图16 所示.由4.2 节中的分析可知，正弯矩作用下，节点的抗弯刚度主要由筒壁的刚度控制；负弯矩作用下，节点的抗弯刚度主要由高强螺栓控制，因此筒壁高度对节点抗弯性能的影响可忽略不计.

5.3 圆柱筒壁壁厚的影响

12～15 号模型的弯矩-转角曲线如图17 所示.当其他参数不变时，节点的抗弯刚度及承载力随着圆柱筒壁壁厚的增加而显著上升.但需要注意，当壁厚过大时，筒壁的刚度过大，节点破坏时筒壁变形很小，可能发生螺栓拉断破坏，节点延性明显下降；当壁厚过小时，在负弯矩作用下可能发生筒壁冲切破坏，节点延性同样较低.因此，在实际工程中应对壁厚进行合理设计，保证节点具有良好的延性，避免节点发生脆性破坏.

图15 圆柱筒壁直径的影响Fig.15 Influence of the outside diameter of hollow cylinder

图16 圆柱筒壁高度的影响Fig.16 Influence of the hollow cylinder height

图17 圆柱筒壁壁厚的影响Fig.17 Influence of the hollow cylinder thickness

5.4 杆件宽度的影响

16～21 号模型的弯矩-转角曲线如图18 所示.由表4 可知，杆件宽度从30 mm 增长至80 mm 时，正、负弯矩作用下节点的初始抗弯刚度分别上升了31.8%和16.9%；抗弯承载力分别上升了23.8%和5.5%.正弯矩作用下杆件宽度对节点受弯性能的影响更为明显.这是由于正弯矩作用下，弧形端板对筒壁变形有约束作用，随杆件宽度增大，筒壁可变形段长度减小，节点刚度明显上升；而负弯矩作用下，弧形端板与筒壁脱开，杆件宽度的影响较小.

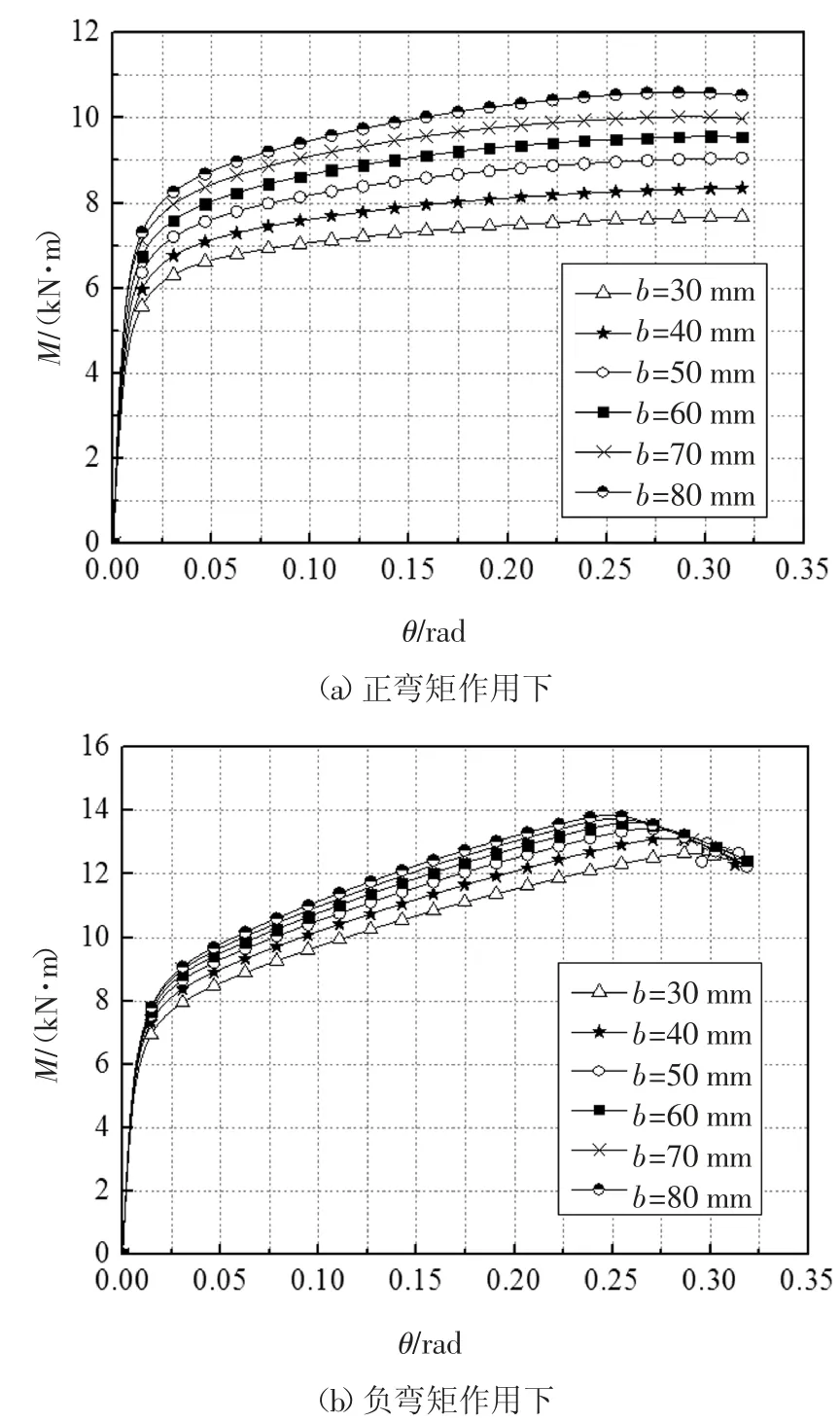
图18 杆件宽度的影响Fig.18 Influence of the rectangular tube width

5.5 弧形垫片宽度的影响

22～25 号模型的弯矩-转角曲线如图19 所示.当其他参数不变时，正、负弯矩作用下节点的抗弯刚度及承载力几乎不受弧形垫片宽度的影响，各曲线几乎重合.因此，在设计时弧形垫片宽度仅需满足构造要求即可.

5.6 弧形垫片厚度的影响

23、26～28 号模型的弯矩-转角曲线如图20 所示.弧形垫片厚度对节点的抗弯刚度及承载力有一定影响，垫片厚度从4 mm 增长至10 mm 时，正、负弯矩作用下节点的初始抗弯刚度分别上升了9.1%和16.5%；抗弯承载力分别上升了9.5%和17.7%.由于垫片与筒壁通过高强螺栓连接，在正、负弯矩作用下两者共同发生弯曲变形（如图12 所示），故增大垫片厚度可提高筒壁的抗弯刚度.

图19 弧形垫片宽度的影响Fig.19 Influence of the convex washer width

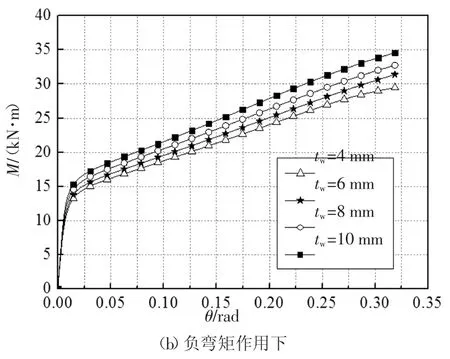
图20 弧形垫片厚度的影响Fig.20 Influence of the convex washer thickness

5.7 螺栓尺寸的影响

由螺栓球柱节点的传力途径可知，螺栓是重要的传力构件.通过29～33 号模型研究了螺栓尺寸对节点受弯性能的影响.由图21 中各节点的弯矩-转角曲线可知，节点的受弯性能随螺栓尺寸的增加而上升，但其影响并不显著. 需注意，29 号模型的弯矩-转角曲线出现负刚度，为避免节点刚度不足，不宜选用尺寸过小的螺栓.

图21 螺栓尺寸的影响Fig.21 Influence of the bolt size

5.8 螺栓间距的影响

34～38 号模型的弯矩-转角曲线如图22 所示.当其他参数不变时，随着螺栓间距的增大，力臂长度增大，节点的抗弯刚度及承载力上升，且正弯矩作用下螺栓间距的影响更为显著.但实际工程中，增加螺栓间距会造成筒壁高度增大，且通常会规定标准螺栓间距，因此可忽略螺栓间距的影响.

图22 螺栓间距的影响Fig.22 Influence of the bolt interval

5.9 加劲肋宽度的影响

加劲肋宽度对节点抗弯刚度的影响通过39～43号模型进行研究.由图23 可知，加劲肋宽度从6 mm增大至24 mm 时，正、负弯矩作用下节点的初始抗弯刚度分别上升了211.7%和197.2%；抗弯承载力分别上升了51.2%和38.3%，且正弯矩作用下加劲肋宽度的影响更为明显.同时，加劲肋宽度大于6 mm 时才能大幅提高节点的抗弯刚度.

5.10 加劲肋厚度的影响

加劲肋厚度对节点抗弯刚度的影响通过39、42、44～46 号模型进行研究.加劲肋厚度从6 mm 增大至12 mm 时，正、负弯矩作用下节点的初始抗弯刚度分别上升了19.0%和18.6%；抗弯承载力分别上升了14.8%和10.9%.对比图23 和图24 可知，增大加劲肋宽度对节点受弯性能的提高作用比增大加劲肋厚度的作用更明显.