PDC钻头旋转流场与非旋转流场的模拟对比研究

2020-02-27

石油矿场机械 2020年1期

(西安石油大学机械工程学院，西安 710065)①

在石油钻井过程中，如果不能及时将岩屑排出井底，会造成岩屑的二次切削，降低钻头寿命，严重时会形成钻头泥包和井底泥包，降低钻井效率。钻头流场的携岩能力与清岩能力与岩屑的质量、大小等因素有关。然而钻头的单相流场不包含岩屑的相关信息，因此，只对钻头的单相流场进行研究是不充分的，不能真实反映井底流场清岩效果。

Well等[1]通过高压钻井试验，研究了JSA、FV、HIS对钻头泥包的影响，并得出相关结论。陈修平等[2]通过对PDC钻头流场岩屑的运移规律的研究，推导了岩屑运输率公式，并建立了最小泥包化下PDC钻头参数优选标准。由于试验需要创建试验装置，前期需要投入大量资金。理论公式对形状多样的PDC钻头不具普遍适用性。因此，利用CFD技术对PDC钻头流场进行研究是一种经济实用的方法。Ail Moslemi等[3-4]通过Fluent-DPM模型对PDC钻头流场进行了研究，通过定义变量Ct研究流场排岩效果，并通过试验对模拟结论进行了验证。将改进后的钻头应用于钻井现场，其ROP有了明显提升。现今模拟岩屑的运移主要有fluent-DPM模型[5-7]和Fluent-EDEM联合仿真[8]两种方法。本次采用fluent-DPM模型对PDC钻头旋转流场与非旋转流场内岩屑运移进行数值模拟。

1 模型建立

为了更为真实地模拟实际钻井中井底流场，本次数值模拟仿真采用较为真实的PDC钻头模型，如图1。井底流域如图2，且其底部为冠状。为了便于计算，建立流域三维模型时不考虑钻头牙齿吃入地层。

2 数学模型及边界条件

2.1 N-S方程

(1)

图2 井底流域三维模型

(2)

(3)

式中：v为运动黏度系数；ρ为流体密度；fx、fy、fz分别为体积力在x轴、y轴、z轴的分量；x、y、z分别为流体质点在t时刻的空间坐标；u、v、w分别为流体质点在t时刻时沿x轴、y轴、z轴的速度分量；p为井底压力。

2.2 DPM模型[9-10]

DPM模型可用来模拟颗粒与气体或液体之间相互作用的问题。曳力计算公式为:

(4)

(5)

(6)

(7)

式中：m为颗粒质量；up为颗粒速度；ρp为颗粒密度；dp为颗粒直径；CD为曳力系数；ρ为液相密度；u为液相速度；Fx为x方向上的其它力；Fd为颗粒受到的曳力；Re为颗粒雷诺数或相对雷诺数；α1、α2、α3、η为DPM模型中的常数。

2.3 边界条件及求解算法

设置钻杆内为入口，压力为16 MPa。环空为出口，压力为10 MPa。围压为10 MPa[11]，钻头转速为12 rad/s。湍流模型为标准的k-w模型，应用DPM模型模拟岩屑在流场中的运移，求解算法为SIMPLE算法，采用滑移网格技术对其瞬态流场进行数值计算。

3 数值模拟仿真

3.1 旋转流场与非旋转流场对比

旋转流场与非旋转流场存在许多的差异，例如流体质点的轨迹云图。PDC钻头井底流线如图3。笔者将本次模拟所得流线图与Smith公司对PDC钻头流场数值模拟所得流线图[12]进行了对比，发现具有较高的相似性。

对比旋转与非旋转流场的流线图(如图4a和4b)，可知流线的差异主要在钻头肩部。当钻头旋转时，从流道流出的流体在惯性力的作用下使得流线发生明显弯曲，并且刀翼肩部产生较大的涡旋，但数量较少。当钻头非旋转时，刀翼肩部产生的涡旋较小，但数量较多。

图3 PDC钻头井底流线

图4 PDC钻头流场流线

在页岩气钻井过程中，由于地层较软，切削产生的岩屑容易黏附于钻头表面，形成钻头泥包。由文献[13]可知，钻头表面的切向力可抑制钻头泥包的生成。

由图5可知，流道内钻头壁面切向力较大，钻头底部中心及刀翼附近切向力较小。钻头表面切向力越大，流体冲击越强烈，岩屑越不容易黏附于钻头表面，从而抑制钻头泥包的产生。通过对比图5a、5b可知，旋转与非旋转流场的PDC钻头底部切向力大小及位置基本相似，这是由于喷嘴出口处流体的线速度远大于钻头旋转对流体产生的线速度。

图5 PDC钻头底部面力

3.2 岩屑的运移与侵蚀模拟

为了保证模拟结果的严谨性，向流场加入固相颗粒时需考虑固相颗粒的初始位置和数量。假设牙齿齿入地层的厚度为2 mm，如图6阴影区域为牙齿端面齿入地层部分，钻头转过角度为θ，钻头单齿切削岩屑的体积可近似表示为式(10)。

图6 钻头齿面

(8)

(9)

Vi=AiLi

(10)

(11)

式中：Ai为阴影部分的面积；Ri为单个牙齿的齿面半径；Vi为单个牙齿切削岩屑体积；Li为钻头转过θ时牙齿滑移的弧长；(x,y,z)为牙齿齿面圆心坐标；V为总切削量；λi为单齿切削岩屑体积占总切削体积的百分比。

假设向流场中加入1 002个固相颗粒模拟岩屑的运移，且在距牙齿底部约2 mm处向流场中插入固相颗粒，其个数可近似表示为表1。其中颗粒最小直径2 mm，最大直径4 mm，平均直径为3 mm。表1中的牙齿编号如图7。

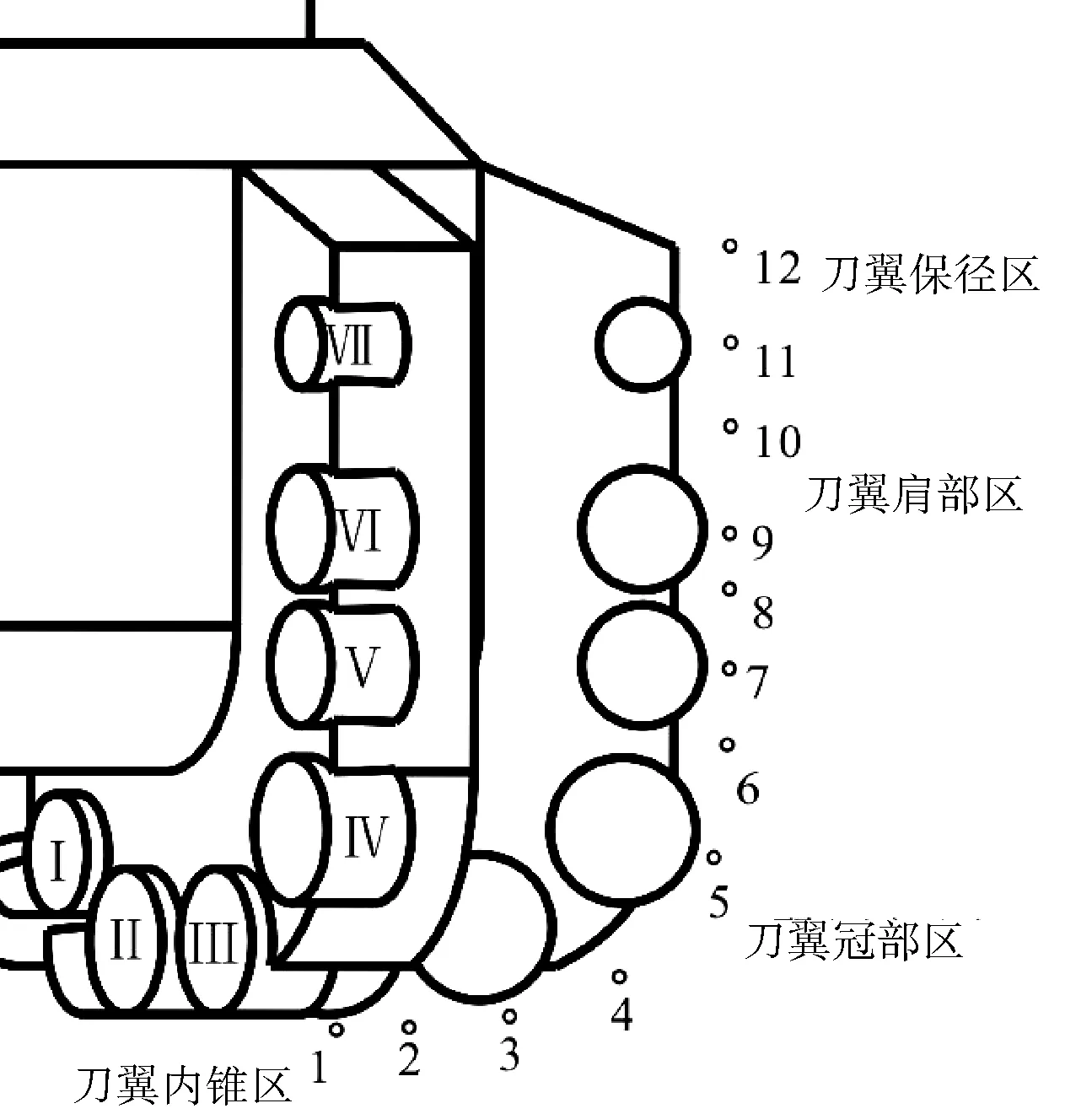
图7 PDC钻头刀翼及牙齿编号

由图8可知，当岩屑从齿面附近进入流场时，靠近喷嘴部位的岩屑可快速地离开井底到达环空，远离喷嘴部位的岩屑在钻井液的作用下返回井底。旋转与非旋转流场内岩屑在钻头的刀翼冠部区与刀翼肩部区都有岩屑的回落，并随流体返回钻头底部。对于旋转流场，部分岩屑运移至环空时其运动轨迹发生明显弯曲，笔者分析这是由于钻头旋转造成的。

表1 牙齿切削占比及岩屑数量

通过对比旋转与非旋转流场岩屑的运移轨迹可知，旋转与非旋转流场岩屑在钻头部位运移轨迹基本相似，但在环空部位岩屑的运移轨迹存在明显差异。对比刀翼肩部流线图与岩屑的运动轨迹，当流线弯曲时岩屑的运动轨迹也会同时弯曲。笔者认为这是由于岩屑的质量较小，其运动特性受流体影响较大造成的。

由图9可知，固相颗粒在旋转流场与非旋转流场都会对钻头刀翼造成侵蚀。旋转流场岩屑侵蚀刀翼背部较多，非旋转流场岩屑侵蚀齿面较多。当侵蚀发生于齿根及刀翼根部时，会造成齿根及刀翼根部的点蚀。

图8 岩屑运移轨迹

图9 岩屑侵蚀钻头云图

为了研究流场内的速度分布对岩屑运移的影响，在流场内选取12个点(如图7)，得到速度分布，如图10所示。旋转与非旋转流场在此区域内会出现2次速度峰值，2次速度峰值分别出现于刀翼冠部区与刀翼肩部区，且非旋转流场速度变化趋势与旋转流场速度变化趋势基本相似。旋转流场刀翼内锥区、刀翼冠部区、刀翼保径区的速度比非旋转流场刀翼内锥区、刀翼冠部区、刀翼保径区的速度大。非旋转流场刀翼肩部区的速度比旋转流场刀翼肩部区的速度大。