广义频分复用的多普勒频移适应能力分析

郭凯丰，吕莹莹，王 颖，郭黎利

(1.中国船舶工业系统工程研究院，北京 100094；2.哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150000)

0 引言

战术数据链在现代战争中发挥着越来越重要的作用，随着各种高新技术的发展和应用，未来空战目标呈现出高速度、大机动和强隐身的特点[1]。正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)技术因其抗衰落能力强、频谱利用率高等优点在战术数据链通信中有着广泛应用。然而在移动速度极高的空空数据链下，严重的频率偏移会影响OFDM系统子载波的正交性，接收端往往需要复杂的频偏估计和同步算法，因此OFDM技术不适用于高速率的空空数据链中[2]。本文研究了在空空数据链下一种改进型的非正交多载波广义频分复用(Generalized Frequency Division Multiplex，GFDM)技术。

GFDM技术是德国德累斯顿工业大学Gerhard Fettweis教授于2009年提出的多载波技术[3]。该技术由于较高的频率利用效率，较低的噪声与杂波干扰水平，对同步、频偏指标要求低的优点，已成为下一代移动通信系统的一种备选载波调制方案，并且可以与预编码或偏移正交幅度调制等多种技术相结合，具有很强的灵活性[4]。GFDM技术的同步、信道估计算法和多输入多输出(Multiple-Input Multiple-Output，MIMO)技术的结合被广泛研究，表明了GFDM技术对未来无线网络的适用性[5-6]。本文首次将GFDM系统应用在空空数据链中，分析推导了GFDM系统的多普勒适应能力，并进行仿真分析。仿真结果表明，GFDM系统有一定的抵抗多普勒频偏的能力。

1 GFDM系统模型

1.1 发射端

GFDM系统发射端在单个时隙内的示意框图如图1所示[7]。

图1 GFDM系统发射端Fig.1 GFDM system transmitter

传输数据经过映射和串并转换为K×M的数据块，其中K表示系统的载波数，M表示每路载波包含的符号数。为了防止成型滤波后相邻子载波上的信号发生混叠，先对每一个子载波上的数据块进行过采样：

(1)

式中，k，m分别为子载波数和字符号数；g[n]为发端原型滤波器。

对数据块进行脉冲成型和频谱搬移，GFDM调制信号可以表示为：

(2)

所以GFDM调制信号为：

(3)

采用矩阵的表达形式说明系统发端的调制过程

gk，m[n]=g[(n-mK)modN]Κα(n，k)，

(4)

A=(g0，0，g1，0，…，gK-1，0，g0，1，…，gK-1，M-1)，

(5)

d=(d0，0，d1，0，…，dK-1，0，d0，1，…，dK-1，M-1)T，

(6)

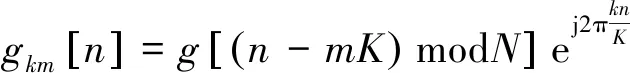
所以GFDM信号的矩阵表达形式为：

x=Ad。

(7)

1.2 接收端

GFDM系统接收端的原理框图如图2所示。

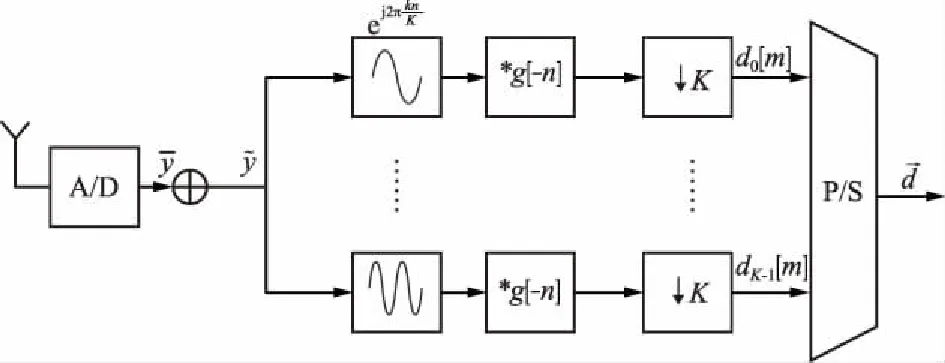
图2 GFDM系统接收端Fig.2 GFDM system receiver

信号经过信道之后可以得到离散时域信号：

y′[n]=x′[n]*h[n]+w[n]，

(8)

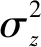
Y′[k]=X′[k]H[k]+W[k]。

(9)

假设GFDM系统的循环前缀长度大于信道最大时延，在接收端已知信道信息和理想同步[8]，去除CP之后并用矩阵的形式表示，式(9)可以表示为：

y=H·x+η。

(10)

对于接收信号y，文献[9]提出的ZF信道均衡能够应用于GFDM：

(11)

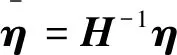
(12)

式中，Ademod是KM×KM维的解调矩阵。3种GFDM线性解调方案是匹配滤波(Matched Filter，MF)解调、迫零(Zero-forcing，ZF)解调和最小均方误差(Minimum Mean Square Error，MMSE)解调。与Ademod对应的3种解调矩阵形式为：

MF解调：

Ademod=AH。

(13)

ZF解调：

Ademod=A-1。

(14)

MMSE解调：

(15)

3种接收方案各有优缺点，MF接收方案能够最大化信息噪声比(Signal-to-Noise Ratio，SNR)，但是滤波器之间不正交导致系统自干扰；ZF接收方案在消除系统的自干扰的同时对噪声进行了加强，并且还存在无法求解调制矩阵逆的问题；MMSE接收方案在自干扰和噪声之间进行了权衡。

2 GFDM系统多普勒适应能力分析

发射端与接收端存在多普勒频移导致子载波之间不正交，使接收端解调出来的信号会有畸变[11]。本文将从建立数学模型的方法深入研究多普勒频移对GFDM系统的影响。由于收发两端存在多普勒频偏，则接收端收到的信号可以表示为：

(16)

式中，γ*[n]为时域接收窗；N为符号数；N(n)为服从均值为0，方差为σ2的高斯白噪声；ε为归一化频偏，定义为频偏除以子载波频率间隔，即ε=Δf/B。

把式(3)发送信号x[n]代入式(16)化简得

(17)

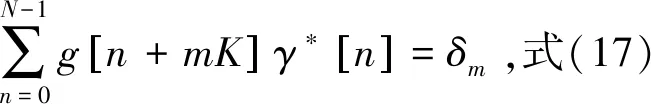
(18)

由式(18)可得，受多普勒影响使得接收到的信号产生误码的原因有3个：由于多普勒频偏导致的信号本身幅度的衰减和相位的旋转；由于载波间干扰导致的信号的误码；信道中的高斯白噪声对信号产生的干扰[12-13]。

3 仿真结果分析

(1)加性高斯白噪声(Additive white Gaussian noise，AWGN)信道下系统性能分析

GFDM调制在AWGN下的误码率性能如图3所示。匹配滤波算法由于忽视了干扰信号的存在，误码率在10-3时其性能比ZF算法差0.5 dB。ZF算法的性能和GFDN系统的理论性能近似，说明ZF算法能够消除GFDM系统的自干扰。由于ZF算法需要求矩阵伪逆，实用性较小。

图3 GFDM系统AWGN下误码率Fig.3 BER of GFDM system under AWGN

(2)多普勒信道下系统性能分析

GFDM系统在多普勒信道下的误码率仿真结果如图4所示，参数设置参考Link16数据链[14]。

图4 GFDM系统多普勒信道下误码率Fig.4 BER of GFDM system under Doppler channel

由于空空数据链中飞机和导弹武器等相对移动速度较高，在接收端产生严重的多普勒频移，记为fd=vfcosθ/c。θ是移动方向和入射波的夹角，fd是多普勒频移，v是发射端和接收端的相对移动速度，f是载波频率，c是光速[15]。不同速度下产生的多普勒频移如表1所示。系统中的多普勒频移不仅使信号在QAM解调时的信号相位发生旋转，不能正确解调数据，还会干扰其他子载波的正确判决，造成子载波之间的干扰。随着多普勒频移的增大，GFDM系统性能下降越严重。误码率在10-3时，多普勒频移fd为1 216，2 433，3 648 Hz时，所需要的信噪比分别为8，9，11 dB。在相同传输效率下，GFDM系统需要的子载波数小于OFDM系统，时域符号宽度长于OFDM，所以具有很好的抗多普勒性能。并且GFDM系统放弃了子载波之间的正交性，减低了由于多普勒频偏导致的子载波之间的干扰。

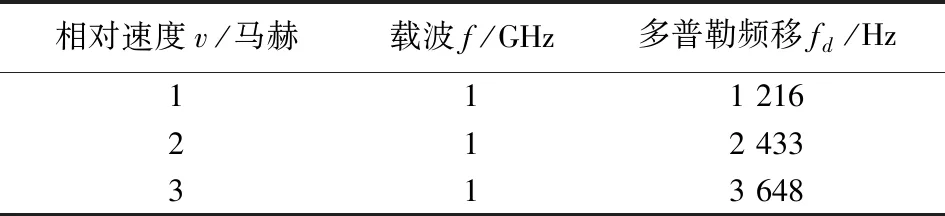
表1 速度和多普勒频移对应关系Tab.1 Correspondence between velocity and Doppler shift

4 结束语

空空数据链由于目标高速移动导致的多普勒频移近些年被广泛研究，本文从多载波调制方式出发，首次在空空数据链中引入GFDM技术实现数据的调制。推导分析了在多普勒频移下GFDM技术的性能，并进行了比特出错概率(Bit Error Ratio，BER)性能仿真。GFDM技术由于放弃子载波之间的正交性，对多普勒频偏有一定的抵抗能力。结果表明GFDM技术可以应用在空空数据链中，为空空数据链提供了一种可适用的调制方式。