双基地噪声雷达中直达波干扰抑制技术研究
2020-02-27鲁振兴洪永彬
鲁振兴,尹 伟,洪永彬
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
0 引言
由于具有优良的低截获概率特性以及无距离模糊特性,从20世纪90年代后期开始,噪声雷达技术逐渐引起了人们的研究兴趣[1-3],并得到了快速发展。
噪声雷达多采用连续波体制,双基地噪声雷达的发射站和接收站间隔一定距离以减小直达波及杂波强度。由于直达波和多径杂波与目标回波在时域上无法分开。在噪声信号的相关处理中,旁瓣(噪声基底)效应非常明显[4],这会造成弱目标被直达波、杂波和强目标旁瓣淹没的现象,从而严重影响系统的作用距离。在实际中,直达波和杂波的抑制非常关键,必须采取多种措施(包括物理措施、空域以及时域处理等)降低直达波和杂波对微弱目标检测的影响。由于物理隔离和空域滤波的抑制能力有限,自适应时域对消成为直达波和杂波干扰抑制的一种必备措施。
常用的自适应时域对消算法包括LMS算法、递归最小二乘(RLS)算法以及相应的改进形式。由于RLS算法的计算复杂度很高,实际应用较少。
LMS算法中,步长参数越大,收敛速度越快,稳态误差也越大[5-6]。其收敛速度与稳态误差始终是矛盾的。然而,在直达波和杂波的对消应用中即使对于较大的步长参数,算法收敛后得到的对消比与维纳滤波方法相差也不大。因此,减小步长对对消比的改善有限[7]。Malanowski[8]曾比较了不同自适应算法在直达波和杂波对消中的效果,表明变步长LMS算法没有明显的优势。
噪声雷达中,参考信号相邻采样点之间存在明显相关性,其自相关矩阵的特征值散度[7]很大,从而造成LMS算法的收敛速度变慢。基于联合过程估计的干扰抑制算法在LMS滤波之前,对输入信号进行去相关处理,从而可以提高算法的收敛速度[9]。
本文通过理论分析,对双基地噪声雷达中基于LMS的直达波干扰抑制算法收敛特性进行研究,给出了对消剩余的收敛曲线。提出基于联合过程估计的干扰抑制算法,通过对输入信号去相关处理提高了算法的收敛速度。
1 基于LMS的自适应干扰抑制方法
1.1 信号模型
假设强多径杂波存在于前M个距离单元之内,那么回波通道的接收信号可以表示为:
(1)
式中,Sd(t)=adSr(t)为直达波信号;ad为直达波信号的复幅度;Sr(t)为接收参考信号;Sci(t)=aciSr(t-τci)为第i个距离单元的杂波信号;aci为该杂波信号的复幅度;τci为其相对参考信号的延迟;Stnc(t)则包含了目标回波、接收机噪声以及远距弱杂波,并且假设目标位于强杂波区之外,即目标延迟τt>τcP。
直达波和杂波均可表示为延迟后的参考信号,于是,可以将直达波和杂波用统一的符号进行表示:
(2)
式中,
1.2 算法原理

J=E[|e(n)|2]=
(3)
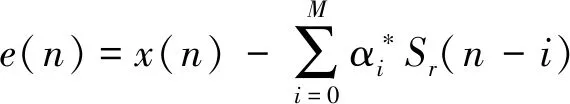
LMS算法利用瞬时梯度对权向量进行调整。假设在n时刻滤波器的权向量为α(n),那么对梯度J(n)的瞬时估计为:
(4)
LMS算法对加权向量的调整方法为:
α(n)+μSr(n)e*(n),
(5)
式中,μ为迭代步长。在算法初始时刻滤波器系数α(0)可以设置为某些先验值也可以设置为0。
根据Butterweck的波理论[10],LMS算法稳定所需要满足的条件为:
(6)
式中,Smax为参考信号功率谱的最大值。
对于中等长度以上的LMS滤波器,式(6)可以保证算法稳定,而对于短滤波器该式也有一定的参考意义[9]。在直达波和杂波的对消中,滤波器长度一般较大(例如,通常需要对消的杂波范围可达数km,对于30 MHz的采样率,滤波器长度一般需要几百阶),可根据式(6)选取步长参数的取值上界。
1.3 算法收敛特性分析
在小步长条件下,LMS滤波器第n时刻的均方误差可以写为[7]:
(7)
式中,
为最优滤波器的均方误差,
Sr(n)=[Sr(n),Sr(n-1),...,Sr(n-M)]T,
p=E[Sr(n)x*(n)],
上角标H和T分别代表共轭转置和转置。
可以得到:
(8)
当n→∞时,均方误差逐渐衰减到如下常数:
(9)
2 基于联合过程估计的干扰抑制方法
由上述分析可知,输入参考信号的相关性对LMS算法收敛速度影响很大,在雷达信号处理中,为了减小采样引起的目标能量损失,一般采样率会大于信号带宽,此时LMS滤波器的输入信号在相邻采样点之间可能存在很大的相关性。采用联合过程估计方法,基于格型预测对输入参考信号进行去相关处理,然后通过基于LMS类的多重回归滤波算法对直达波和杂波估计,提高算法收敛速度。
2.1 格型预测
格型预测是一种常用的去相关方法,它可以将参考信号转化为彼此之间相互正交的后向预测误差,并且信息量没有损失。去相关之后可以利用多重回归滤波器将后向预测误差进行线性组合,从而实现对直达波和杂波信号的拟合相消。
格型预测器结构如图1所示,其中,fi(n)和bi(n)(i=0,1,...,M-1),分别代表参考信号Sr(n)的前、后向预测误差,κi为反射系数。零阶预测误差f0(n)=b0(n)=Sr(n),并且前、后向预测误差之间的递推关系如下:
(10)
bi(n)=κifi-1(n)+bi-1(n-1),
(11)

格型预测器输出的后向预测误差bi(n)之间相互正交,即:
(12)
式中,Pi为i阶预测误差功率。

图1 格型预测器结构Fig.1 Structure of lattice filter
对于非平稳输入信号,利用梯度自适应格型(GAL)算法对反射系数进行更新,通过最小化前、后向预测误差功率之和,得到反射系数的递归形式[11]:
(13)

|bi-1(n-1)|2],
(14)
式中,β为接近于1但是小于1的正数。
2.2 多重回归滤波算法
对参考信号进行去相关之后,通过多重回归滤波器对直达波和杂波信号进行估计。多重回归滤波器的系数更新可以采用LMS类型的算法。因为此时各抽头输入之间变得不相关,所以LMS类型算法的收敛速度会得到明显提高。
NLMS算法采用||b(n)||2作为归一化参量对回归系数hi(n)进行如下调整:
式中,b(n)=[b0(n),b1(n),...,bM(n)];μ为步长参数;·代表向量的模。
如果在hi(n)的调整中利用λi+1将步长进行归一化,那么不同的收敛模式将具有相同的收敛速度。考虑到λi+1=Pi,对于固定系数的格型预测器,采用SNLMS算法对回归系数进行调整:
3 仿真验证
3.1 LMS干扰抑制算法的收敛分析
假设参考信号为单位方差的白噪声,需要对消的杂波范围为0~2 km(双基地距离),直达波和杂波的总强度为58 dB,Stnc(n)的大小为0 dB。信号的采样率为30 MHz,LMS滤波器的长度为200阶。
图2给出了此时对消剩余的收敛曲线,其中仿真曲线为10次蒙特卡洛仿真平均得到的结果。可以看出,仿真曲线与理论结果一致,并且步长参数越大,算法收敛越快,但是对于不同的步长,收敛后对消剩余的区别并不明显,这是因为收敛后的超量均方误差相对Jmin小很多。一般情况下,如果超量均方误差可以达到与Jmin相同的水平或者比Jmin更小,可以认为得到了较为满意的对消结果。

图2 非相关输入情况下的对消剩余收敛曲线Fig.2 Convergence curve of cancellation residue for uncorrelated input
如果参考信号为低通滤波后的噪声调频信号,其带宽为10 MHz,图3给出了此时对消剩余e(n)的收敛曲线。可以看出,在相同步长条件下算法的收敛速度变慢。这是由于此时参考信号的相邻采样点之间具有相关性,相关矩阵Rr的特征值扩展明显变大(其最大特征值约为3.13,最小特征值约为7.5×10-10)。较小特征值对应的自然模式收敛较慢,从而导致算法的整体收敛速度变慢。
在图3(a)中,5 ms之后算法基本达到收敛。这样的收敛速度对于静态杂波来说已经足够,但是如果杂波的多普勒频率较大,5 ms的收敛时间可能是不满足要求的。例如,在强风状态下,植被的速度谱展宽可达0.5 m/s[12],对于10 GHz的工作频率,相应的杂波多普勒频率为33 Hz,此时上述收敛速度就显得过慢。

图3 相关输入情况下的对消剩余收敛曲线Fig.3 Convergence curve of cancellation residue for correlated input
3.2 联合过程估计算法的收敛分析
3.2.1 固定反射系数条件下的收敛分析
假设最远杂波的(双基地)距离为2 km,直达波和杂波的总强度为46 dB。在样本数为1 000的情况下,计算得到相应的反射系数。
在联合过程估计中,格型预测器采用该反射系数对输入参考信号进行去相关,得到的对消输出结果如图4所示,其中FL-SNLMS和FL-NLMS分别代表基于固定系数格型预测器的SNLMS算法以及NLMS算法。需要注意的是,由于自适应过程中输出信号起伏较大,为了便于观察,对对消结果进行了100点(3.3 μs)的平滑处理。
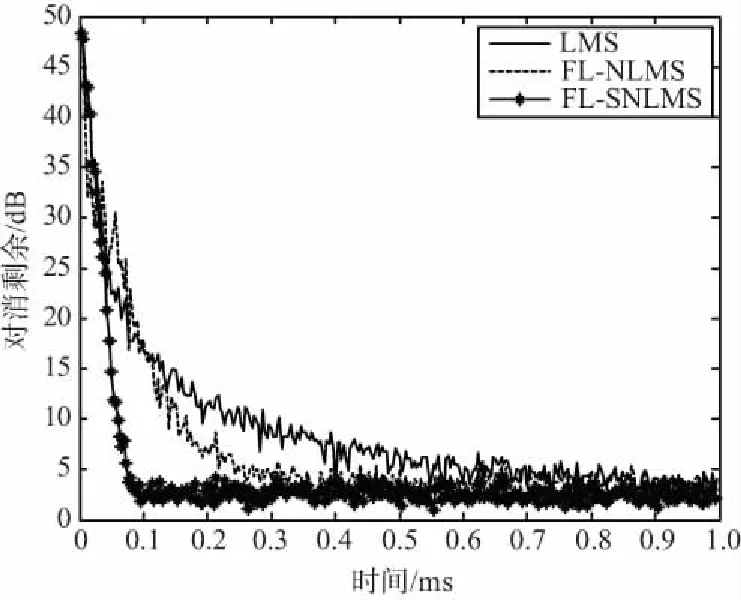
图4 固定反射系数条件下联合过程估计算法的收敛曲线Fig.4 Convergence curve of joint process estimator for fixed reflection coefficient

虽然LMS算法在初始阶段收敛较快,但是随着迭代次数增加,其收敛速度逐渐下降,与其他算法相比,在0.3 ms之后其对消剩余最大。FL-NLMS算法在初始阶段收敛速度较慢,但是在0.4 ms之后基本达到收敛,最终的对消剩余在3 dB左右。FL-SNLMS算法具有最快的收敛速度,仅需0.1 ms就可以达到收敛,收敛后的输出误差与FL-NLMS算法基本相同。另外,可以看出,FL-SNLMS算法的收敛速度近似是恒定的,与理论分析一致。
3.2.2 GAL算法下的收敛分析
当反射系数采用GAL算法进行自适应更新时,图5(a)给出了相应的NLMS和SNLMS算法收敛曲线。在GAL算法中,参数β=0.99,z=0.001;NLMS和SNLMS算法的参数设置与上述仿真相同。
在图5(a)中,GAL-NLMS算法和GAL-SNLMS算法的初始收敛速度较快,但是与LMS算法相比,它们的对消剩余都很大。这是由于GAL算法每对反射系数进行一次更新,NLMS算法和SNLMS算法就需要重新对回归系数进行调整。所以在联合过程估计中,GAL算法必须在一段时间之后停止对反射系数进行更新。
如果反射系数在0.17 ms之后停止更新,GAL-NLMS和GAL-SNLMS算法的输出误差会快速收敛到较低的水平,如图5(b)所示。此时这2种算法会比LMS算法更快达到收敛状态。

图5 GAL算法下的收敛曲线Fig.5 Convergence curve of gal algorithm
4 结束语
在双基地噪声雷达中直达波和近距杂波抑制过程中,由于参考信号自相关矩阵的特征值扩散较大,传统LMS类对消算法收敛速度很慢,难以满足低速杂波抑制的需求;本文采用格型预测器对参考信号进行去相关处理,提高算法的收敛速度。但是,对于平稳的参考信号最好采用固定的反射系数,采用基于GAL的抑制算法会引起对消剩余的增大。
