MATLAB在线性代数教学中的应用

（陆军步兵学院基础部 江西·南昌 330100）

线性代数作为高校教育中的一门基础学科，是学生进入学校后较早接触的学科之一。除了让学生掌握线性代数基本知识，其普遍的应用性也对学生的计算能力提出了更高的目标。例如，线性变换知识在机器翻译和图像搜索技术中的应用，矩阵理论在密码学中的应用。然而，由于线性代数课程的计算复杂性较高，因此学生很难将其应用到实际生活中。而MATLAB语言拥有较好的数值计算性能，因此使用MATLAB语言辅助线性代数教学，能有效的帮助学生将所学的理论知识应用到实践中去。

1 MATLAB在线性代数教学中的应用

根据同济大学编写的线性代数教学内容，MATLAB在线性代数中的应用具体可以体现在以下几个方面。

1.1 矩阵与行列式的计算

在线性代数所有的知识点中，矩阵与行列式是整个学习内容中两个最基本的知识点，也是后续内容的基本点。在MATLAB内，输入一个含指定元素的矩阵方法是：矩阵中所有元素都包含在方括号内，同一行元素间通过逗号或空格相隔，不同行元素间通过分号或者直接按换行键进行相隔。例如输入一个2×3的矩阵命令：，输出的矩阵为：

学生可以通过定义法、降阶法、公式法、三角化法、性质法等对行列式进行计算。然而在实际问题里，行列式的阶数往往较大，这时要对行列式求解就比较困难。为此，可通过引进MATLAB语言内的行列式求解函数对其进行运算。

（2）矩阵行最简形：对矩阵使用初等行变换化行最简形经常用在求解线性方程组中。在MATLAB的内部函数里，提供了一个将矩阵变成行最简形的函数，其调用格式为：

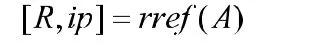
（3）矩阵秩的计算：矩阵的秩经常用于求解线性方程组上。MATLAB提供了一个用于求矩阵秩的内部函数：。比如判断由例2中矩阵的列向量构成的向量组的线性相关性。其MATLAB命令为：

（4）矩阵逆的计算：逆矩阵在实际问题中有许多应用，比如可用于密码学中。在线性代数中，求解逆矩阵的技巧主要是伴随矩阵法和初等变换法。在MATLAB语言的内部函数里，求逆的函数有：用于对一个的满秩方阵求逆，的长方形矩阵求广义逆。

1.2 线性方程组的求解

对线性方程组求解是整个线性代数课程内容中的一个重要内容，也是学生比较感兴趣和困难的内容。在线性代数中，有多种技巧对一个线性方程组求解，例如消元法、初等变换法、克莱默法则、逆矩阵法等。然而手工计算非常的繁琐，不利于学生在实际工作中进行应用。这时，就可以通过使用MATLAB编程对线性方程组进行计算。

1.3 正交矩阵

1.4 特征值与特征向量

特征值与特征向量在工程问题中有着广泛的应用，比如振动问题、稳定性问题，都能转化成计算特征值与特征向量形式。然而，对于四阶或四阶以上的方阵，通过理论方式求解特征值与特征向量非常繁琐。因此，在学生掌握基本概念的基础上，通过引入MATLAB内计算特征值与特征向量的函数对其进行求解，这样能够较好地增加学生的学习乐趣，提升处理实际问题的能力。函数的调用格式为：

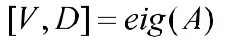
例4：求例1中的矩阵A的特征值与特征向量。

2 MATLAB在线性代数教学中的几点注意

通过在线性代数的课堂教学过程中使用MATLAB编程，能够极大的增强学生的应用能力。然而，老师在教学中应该注意下面几点：

第一，注重线性代数基础知识的教学。由于线性代数是一门基础课程，理论知识的掌握程度关系到学生其它内容的学习；其次，具备较好的理论基础也有利于学生通过MATLAB解决现实问题。从而，在教学过程中，老师要着重对线性代数基础知识的讲解。

第二，具备MATLAB编程基础知识。掌握MATLAB基础知识，可以有效的提高老师的教与学生的学的效果。因此，在讲授完线性代数基础知识后，可以在介绍一部分MATLAB相关内容，来帮助学生提高对线性代数内容的应用能力。

第三，认清MATLAB是辅助教学工具。在线性代数的教学里使用MATLAB编程，教师应该注意避免走入极端。即在教学中偏中用MATLAB对线性代数问题进行计算，对其计算过程和原理不进行讲解。这虽然增强了学生的实践能力，但是却降低了线性代数的理论基础，不利于学生对线性代数知识的学习。因此，老师在教学过程中，应该时刻认清MATLAB在线性代数的教学过程内的地位。

线性代数作为一门理论和实践联系较为紧密的课程，具有较好的理论性和实用性。因此，通过在线性代数教学中应用MATLAB编程，不仅可以极大的简化问题的计算过程，增强学生处理现实问题的能力，而且可以提高学生在课堂上学习的积极性。所以，将MATLAB引入到线性代数的教学中，可以有效的帮助学生落实学以致用的目标。但是，老师在教与学生在学的过程中，要强调以线性代数理论知识为主，MATLAB语言只是一个辅助工具，做的两者的协调统一。