基于机器学习算法模型的巫山县洪水灾害研究*

牟凤云，杨猛，林孝松，龙秋月，李梦梅，何勇

(重庆交通大学建筑与城市规划学院，重庆400074)

山区地形地貌复杂、气候多变等诸多因素导致洪水灾害频频发生，如何有效预防洪水灾害是亟待解决的问题。大数据已应用于各大学科领域，而机器学习具有多学科、多领域、多算法等优势，能有效地挖掘大数据潜在的信息，其中，随机森林模型(RF)、K-means聚类模型、自回归滑动模型(ARMA)等已广泛应用于大数据平台[1]。加上山区地貌类型复杂、流域单元数据量大等特性，利用机器学习能够有效预测出山区洪水演变规律，实现山区洪水灾害防治与预警。

已有研究中，在模型运用方面，胡胜等[2]、吴裕珍等[3]采用SWAT模型利用CFSR气象数据对小流域进行水文模拟，以及对降雨-径流水质进行研究，并做出适用性评价；刘志方等[4]、顾西辉等[5]，利用突变检验方法构建小气候对流域产流与汇流研究以及降雨-径流关系，通过水文综合模拟系统(HIMS)考虑流域产流、汇流、蒸发、下渗等水循环过程；理论研究方面，现有研究表明，降雨是导致滑坡主要因素，降雨[6-10]导致植被覆盖较少、坡度较陡等区域滑坡泥石流发生。文献[11-12]结合多方面因素研究洪水灾害，进行洪水灾害风险评估。以上学者研究，多在于数理统计与规律总结，将研究结果进行空间表达方面有待研究，且在机器学习方面有待结合。本文针对山区降雨-径流演变所涉及的水文参数大数据，引入机器算法进行数据挖掘与统计分析，并结合多学科进行地理空间信息可视化分析。

以巫山县为研究对象，首先，选取机器学习RF、K-means与ARMA算法模型，对研究区降雨-径流演变过程所形成的12 369个子河段，共计500条河流。进行水文参数关系拟合，并利用GIS技术，进行水文参数空间信息表达；再者，结合研究区地理环境、土壤类型、土地利用类型等指标，多方面探讨机器学习算法在山区降雨-径流模拟过程实用性。最后，综合机器学习优势和研究区地理环境特性，运用算法进行研究区洪水灾害分析，最终研究结果可为区域洪水灾害防治、公路洪灾预警提供科学依据。

1 研究区域与方法

1.1 研究区概况

巫山县位于重庆市东北部，与湖北接壤，地处三峡库区腹心，地理坐标介于30°46′-31°28′N，109°33′-110°11′E之间。截至2017年底，户籍人口63万，共24个乡镇；巫山县属亚热带季风气候，降雨充沛，四季分明，年平均温度在18.4 ℃左右，年均降雨量高达1 041 mm；山区溪河众多，常年因降雨致使洪水灾害频发。地形地貌类型复杂，属典型的喀斯特地貌，地形起伏大，最高海拔达2 698 m，最低海拔仅63 m。2015年4月，巫山县11个乡镇遭受不同程度洪水灾害，农作物受灾面积达100 hm2，直接经济损失100余万元；2017年7月，巫山县发生暴雨洪水灾害，降雨量达175 mm以上，官阳镇、红椿乡等乡镇发生不同程度洪水灾害。

1.2 研究方法

机器学习为人工智能核心算法，涉及多学科领域，具有自动组织和模拟功能，广泛应用于数据统计、资产评估预测等多方面[12-13]。常见的机器学习算法为监督学习、非监督学习、深度学习3类。监督学习算法中，神经网络、决策树算法最为经典，常见的模型有随机森林模型、线性回归模型等，K-means聚类算法模型在非监督学习算法最为常用，深度学习中马尔可夫链研究较多。

水文参数信息提取提取过程中，产生大量河段数据，需要进行有效、精准的分类，而随机森林模型刚好具备数据精准分类特性，不仅能够将大量数据河段数据进行分类，还能进行水文参数重要性预测；研究区提取的12 369条河段，出现大量数据冗余，而在机器学习算法模型中，K-mean模型具有去除冗余数据特性。选取K-mean算法对研究区河段数据进行聚类，去除冗余值；在研究降雨-径流演变过程中，由于不同时刻降雨量不同，水文参数变化率存在着差异，而ARMA模型能够有效地在时间序列上预测数据变动情况，故选取ARMA模型进行降雨-径流时间序列预测。

1)随机森林模型Random Forest(RF)[12-13]。RF模型为各类决策树算法总和，而决策树可为大数据统计分类提供有效、精准的分类算法。鉴于此，结合RF模型，对研究区降雨-径流水文参数统计数据，进行数据挖掘，获取每一河段预测值，通过预测值进行河段分类，最终拟合出最为精确降雨-径流关系式，并以此预测山区洪水致灾范围。

2)K-means模型[14-16]。K-means模型以特定距离对统计数据进行硬性聚类，在大数据分析中广泛运用。该算法基本思路为：将降雨-径流获取的水文参数中作为K个样本，在n个河段中进行分类。K-means模型的运用，能够减少数据冗余值，得到有效的研究参数。

3)ARMA模型[15-16]。时间序列ARMA模型为滑动自回归模型，该模型将回归分析与滑动平均模型相结合，能够有效地预测数据变动情况。结合该模型特性，将不同河段编号作为时间序列，以RF模型、K-means模型和水文参数量化指标为回归预测值，在不同降雨强度下对降雨-径流进行时间序列预测分析。

1.3 山区河流水文参数及经验公式建立

受气候、下垫面、人类活动等因素影响，部分区域不会直接形成径流，需经下渗、填洼、蒸发等汇流过程形成，径流地理环境特性，使其流速、水位变化存在差异。在理想条件下，综合国内外雨洪计算方法[13-16]，基于天然河道汇流平均速度与出水口断面平均流速公式，联立曼宁公式在天然河道构建的平均流速计算公式[15-18]，考虑岩石、植被、泥沙等因素对山区河流的阻碍作用以及流域汇流累计量的折减效应(汇流参数)；山区河网密集错综复杂，基于DEM提取的河网虽有等级信息却缺乏高程变化，然而河流比降却能反映河流的高程变化，即利用河流比降来表示河流纵断面高程变化。河流比降的表示与坡度相同，其关系式为河流轴线河底或水面的高程与该河流长度的比值，考虑到山区地形地貌因素，将河流划分为若干个子河段求取平均比降；结合研究区地形地貌、流域地理环境和土地利用等因素，确定河段阻碍系数并通过研究区12 369条河流进行关系拟合，择取机器学习算法模型，研究降雨-径流演变规律，并拟合水文参数之间关系。

1.4 数据来源及处理

综合考虑山区地理环境特性，确定研究区地形地貌、河流比降、山区河流阻碍系数(糙率)、汇流参数、土壤特性、植被覆盖等为流域环境指标，降雨强度(流速、水位、流量)、径流系数、汇流参数等为水文参数指标。基于GIS技术，以研究区分辨率为30 m DEM数据，进行水文参数信息提取，并以流域汇流累积流量为河流等级划分依据，择取栅格单元2 000流量将河流划分为6个等级，进而计算出汇流累计量、小流域等水文信息；选取2015年夏季研究区OIL遥感影像，对其进行植被覆盖和土地利用类型信息提取。研究涉及水文参数经验公式，其理论与推导来源于国内外经验公式，气象水文数据来源于巫山县观测站点。

2 结果分析

2.1 模型预测结果精度验证

需要对通过机器学习算法模型预测出的结果进行精度验证。巫山县共52个观测站点，由于预测河段样本数量较大，且每个站点能够统计到100以上条河段实际数据。在研究区中进行均匀选取，并能够覆盖整个河段观测站点，最终选出10个站点进行结果验证。以实测数据为标准进行预测结果对比验证(图1)。验证结果显示：预测数据与实测数据整体上基本吻合，部分数据存在偏差现象；流速与水位预测结果准确性比预测流速高，相较于流速与流量预测结果，水位预测准确性最高。

2.2 研究区水文参数预测与分析

降雨-径流演变包含地形地貌、降雨强度、土壤特征、植被覆盖以及水库湖泊调节等诸多因素，择取机器学习算法RF模型、K-means模型与ARMA模型，进行研究区降雨-径流水文参数拟合，探究降雨-径流演变规律，测定参数结果如表1所示。以研究区12 369条河段为研究对象，通过RF模型进预测统计，结合RF模型与K-means算法模型，进行径流水文参数分类统计，拟合河段数量与河流等级关系。统计结果中，不同等级径流流速、水位变化有所差异，降雨阈值为25、75、125、200 mm流速、水位拟合结果最好。

不同降雨强度阈值下，水文参数随河流等级、径流曲线数(CN)、河流阻碍系数不同而随之发生变化，从图2(a)河流等级相对流速变化可以看出，随着河流等级增加，流速变化率整体上呈现下降趋势，且降雨强度越大，等级较低河流变化幅度越大；1～3级河流变化幅度最大，降雨量在25～75 mm区间，其变化幅度最小，降雨75～200 mm，等级变化相对集中；预测结果中，变化最为剧烈的为2～4级河流。河流等级变化对河流流速变化预测较为客观，需对研究区整体河流进行分类与预测，图2(b)为巫山县整体河流流速变化趋势，在研究区6个等级河流中，流速变化主要为1～3等级河流，且降雨阈值为200 mm时，流速变化幅度最大；1～4等级河流中，部分区域流速突变显著，由此可见，山区河流流速、水位变化率最为明显。

图1 巫山县模型预测结果对比验证图Fig.1 Comparing and authenticating charts of prediction results of Wushan County

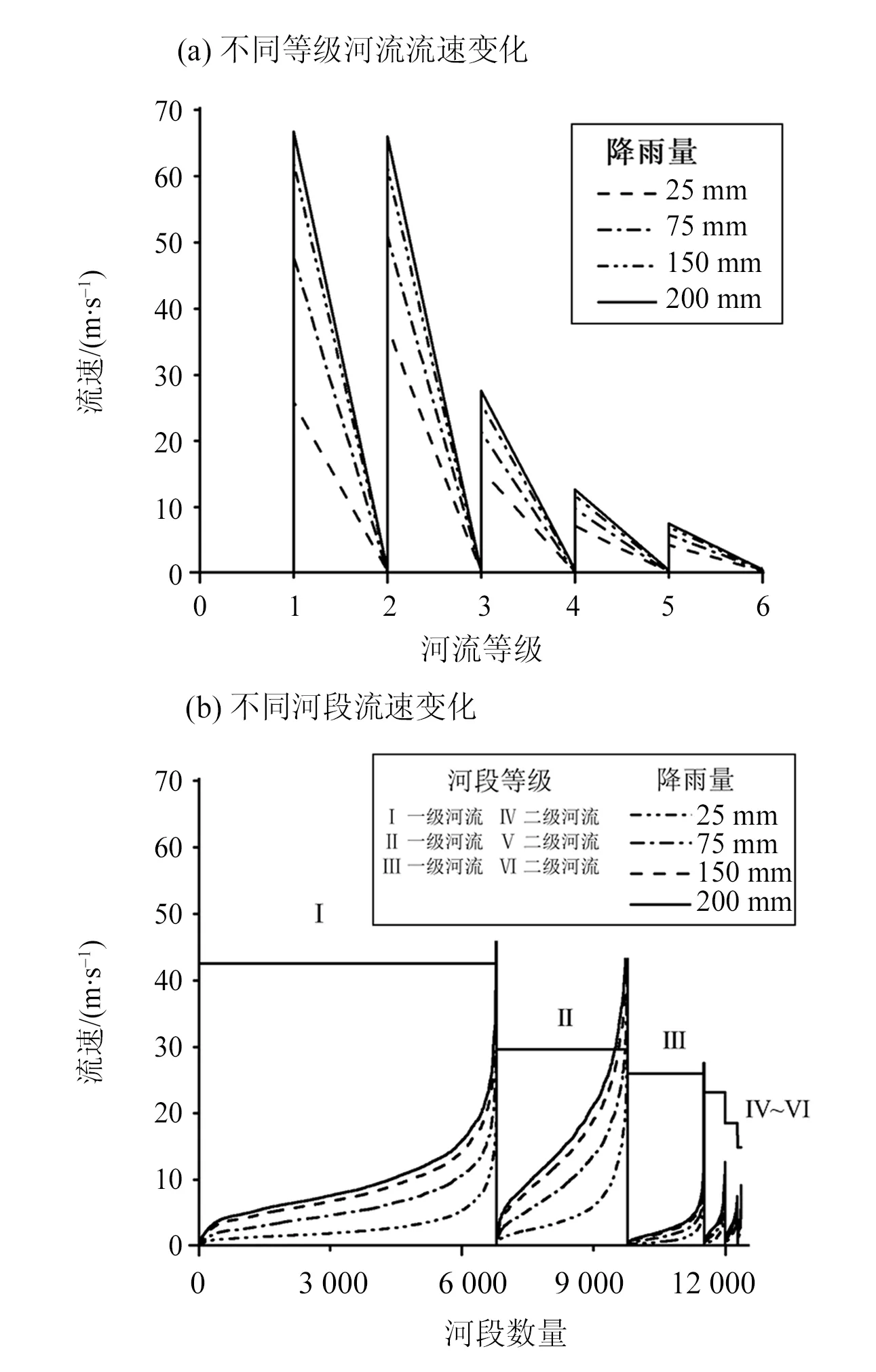
图2 巫山县不同降雨量下河流与河段流速趋势变化预测Fig.2 Prediction of flow velocity trend of river and reach under different rainfall in Wushan County

预测结果中，土壤类型指标重要性最高，其中黄棕壤平均预测值达8 835，效应值2 083，影响最为强，而水稻土与黄壤平均预测值为7 521，效应值为1 368，影响力次之。而土壤类型在河流、潮土、石灰岩、紫色土、裸岩平均预测值为6 581，效应值为-170，影响力较低；土地利用类型中城乡、工矿、居民用地、未利用地、耕地平均预测为6 751，效应值为558，林地、水域、草地平均预测值5 865，效应值为-327，可见林地、草地保水能力较强，对其水流阻碍能力也强，其预测值低于其他类型用地；当河流比降> 0.002时，平均预测值达8 134，效应值为612。而当河道比降≤0.001时，平均预测值为5 539，效应值为-1 438。可见，河流比降预测重要性虽强，但效应值却很低；而分类预测结果中，25、125和200 mm流速预测结果最为精确，统计结果详见表2。

表1 巫山县山区河流参数统计表Table 1 Statistical tables of mountain rivers of Wushan County

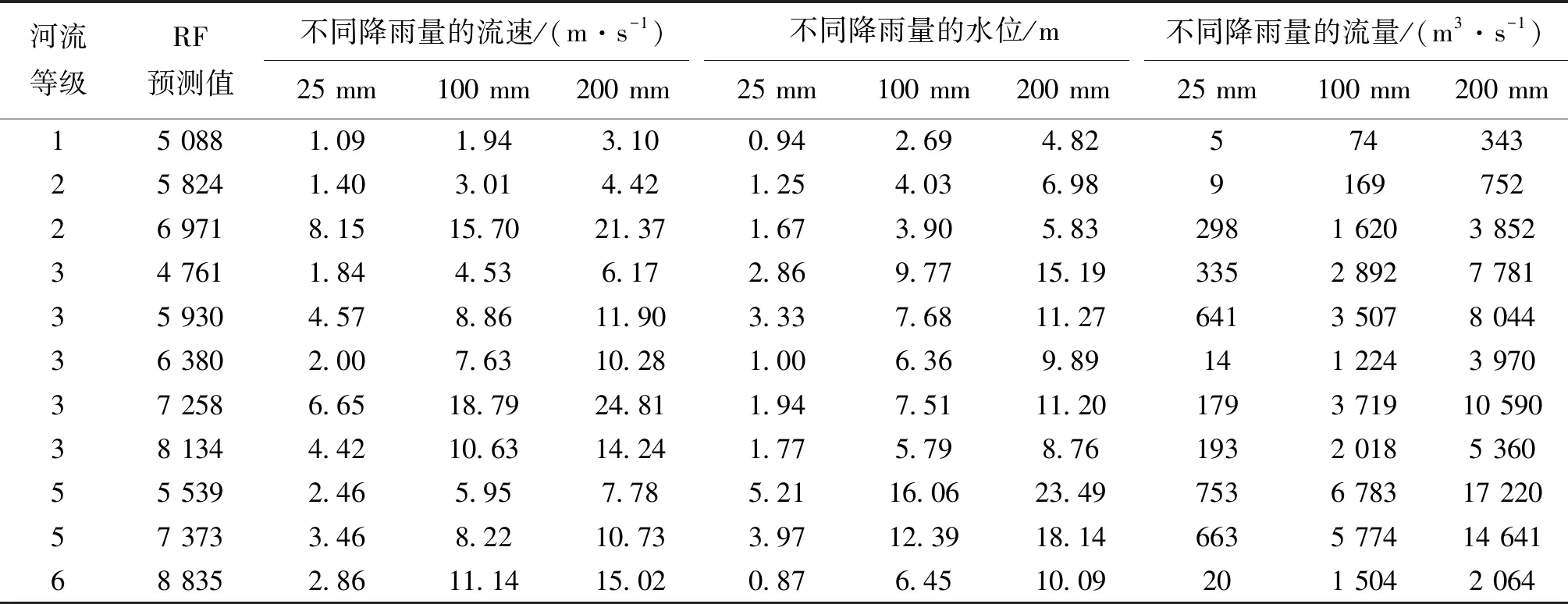
表2 巫山县不同降雨量的流速、水位、流量巫山县RF模型预测结果Table 2 Prediction results of RF model of velocity, water level and discharge in Wushan County under different rainfall

降雨强度达100 mm及以上时，研究区流速发生明显变化。而降雨强度在100～175 mm时，流速变化率度最快，且在降雨175 mm之后，变化幅度有所减缓；在降雨强度较少情况下，部分流域未能形成径流，出现区域流速为零现象，降雨量小于25 mm时，流域流速变化率几乎接近于零值，降雨强度在25～50 mm之间，研究区流速变化率逐渐变快，在50～75 mm之间，流速变化率略为增快；从12 369子河流流速变化曲线可以看出，降雨量在0～50 mm之间，径流流速变化集中在0～10 m/s，且变化幅度较小；降雨在50～100 mm，流速变化集中在10～20 m/s之间，变化幅度逐渐增强；降雨在100～200 mm之间，流速变化集中在20～40 m/s之间，变化幅度明显增强；研究区流速整体上集中在0～40 m/s之间，其变化幅度逐渐增强。

径流水位与流速变化趋势整体相同，降雨强度阈值为125 mm时，水位发生明显变化，降雨强度在150～175 mm区间，相较于同等雨量流速相比，水位变化更为强烈，而降雨在75～125 mm区间时，流速变化幅度大于水位；研究区水位变化集中在0～30 m之间，变化幅度相较于流速变化较小，但水位突变区域比流速突变区域多(集中区域模拟以外曲线即为突变区域)；降雨强度在0～75 mm流速与水位变化基本相同，75～125 mm水位变化幅度大于流速，而降雨强度在125 mm之后，流速变化幅度则大于水位。

2.3 基于ARMA模型的洪水灾害参数指标预测

RF模型具有分类精度高、指标预测准确等特性。以研究区12 369条河段为研究对象，通过RF模型进行雨洪流量、流速、水位线性回归关系拟合，进行不同降雨强度情景下流速、水位、流量关系拟合；再者，在不同降雨强度下，进行河流等级回归拟合，最终显著检验R2>0.94；最后，通过K-means聚类与RF统计分析结果，建立流速、水位、断面流量之间转换关系。RF模型指标重要预测结果中，河流比降、河流等级重要性较高，将其参数以时间散点为时间序列，通过ARMA模型参数预测结果进行对比分析。

从图3可以得出，在不同降雨强度情况下，水位变化率最小，而流速变化率最为明显。由此可见，水位变化更易引发洪水灾害，而流速变化，主要表现为构筑物的冲击效应。

图3 巫山县山区河流量化关系拟合图Fig.3 Fitting diagram of quantitative relationship of mountainous rivers of Wushan County

由于洪水灾害制灾因素在时间序列上存在变动情况，不同时间降雨量不同，导致水文参数变动情况不同。通过ARMA模型模拟水文参数在时间序列上的变化。根据水文参数在空间上排序为时间预测目标值，再以不同降雨强度下水文参数量化指标为回归预测值，并对回归残差值进行处理，最终模拟出水文参数指标在时间序列上的回归预测模型(图4)。

图4 巫山县ARMA模型水文参数拟合图Fig.4 Fitting of hydrological parameters based on ARMA model of Wushan County

巫山县以山地、丘陵为主，然而河流比降受地形因素影响，河流等级却受汇流累计量影响，因此回归性较差；河流比降回归值介于0.1～0.2之间，回归性较好；河流等级回归性较差区间为在0～0.8，其中0～2 000、8 000～12 000河段回归拟合较好；通过ARMA模型分析，山区径流比降、流量回归拟合较好，流速、水位、河流等级变化幅度大；0～2 000、8 000～12 000段河流回归性较好，且不同河段流速、水位、流量变化与河流等级相关，等级较低河流，其水位、流速变化率最为快，而流量变化率却无显著变化。

ARMA模型拟合结果显示(图4)，流速整体回归值在0～0.4之间，在0～12 369条河段中，径流流速变化幅度相较于水位变化较小，0～6 000条河段变化幅度较小，6 000～12 000条河流变化幅度较大；水位回归值在0～0.8之间，整体变化幅度较大，在0～2 000、10 000～12 000河段变化幅度相对较小，2 000-8 000水位变化幅度较大；流量回归变化相对于流速、水位变化幅度最小，0～6 000河流流量变化幅度较小，6 400～8 000变化幅度最大，8 000～12 000变化强度有所减弱；通过ARMA模型对研究区河流流速、水位、流量回归模拟可知，流速、水位变化幅度较大，而流量变化幅度较小，可见山区洪水灾害主要为流速与水位作用所致。

2.4 研究区洪水灾害预测结果空间特征分析

巫山县暴雨频发，引发的洪水灾害频繁。根据山区河流洪水突发迅猛、地形地貌复杂等特性，择取统计时间24h的实测雨量25、75、125、200 mm，以巫山县12 369河段为研究对象，结合ArcGIS空间可视化技术，通过RF、K-means与ARMA模型模拟结果进行空间可视化(图5)。综合得出，在不同降雨强度下，巫山县流速水位主要集中在等级较高河流，而在山地区域，流速的空间变化更为剧烈，巫山县中南部与西北部为洪水灾害频发区域。

流速空间变化率图5(a，b,c)可知，降雨强度临近25 mm时，研究区内径流流速主要集中在中部及长江上游一带变化，且变化幅度较小，而在西北部区域，部分径流流速出现突变现象；当降雨强度增强至125 mm时，研究区整体流速主要集中在0～22 m/s之内，部分区域达46 m/s，且整体流速为25 mm流速一倍，南部地区流速有增强趋势；降雨强度达200 mm时，即为大暴雨情景，流速变化明显增强，部分区域流速达58 m/s，西北部、中南部流速明显增强，且流速在20～58 m/s之间变化，洪水灾害发生可能性极大。

相较于流速变化率，水位变化率主要集中在长江及其西北地区，图5(d，e，f)可知，研究区径流整体水位深度变化介于0～30 m之间；降雨强度越小，水位变化幅度越小；等级较低河流在降雨强度为25 mm时，水位几乎无变化，主要变化区域集中在长江流域及水库区域；当降雨强度增强至125 mm时，径流水位发生明显变化，变化区域主要集中在东北部与中南部，东北部径流水位呈现上升趋势，研究区径流最高水位达20 m；降雨强度达200 mm时，南部与东北部水位明显上升，整体水深升至降雨25 mm时水位一倍。根据站点统计数据与预测结果对比认证，以及研究区洪水灾害数据发生情况，综合得出：当水位到达到1.2 m时，即降雨强度为125 mm时，研究区部分区域出现轻度洪水灾害：研究区水位升至10 m时，降雨强度介于125～175 mm之间，出现中度洪水灾害；当水位超过10 m时，降雨强度在175 mm以上时，研究区出现严重洪水灾害。

图5 巫山县流速、水位空间量化图Fig.5 Spatial map of velocity and water level of Wushan County

3 结 论

通过RF、K-mean与ARMA等机器学习算法与模型，对研究区12 369条河段进行统计与分析，得出了其模型能够精确的拟合出研究区水文参数流速、水文、流量之间转换关系，并且有效预测出区域流速、水位变化率。结合GIS空间可视化技术，对降雨-径流水文参数空间可视化分析，综合考虑研究区地理环境要素及孕灾环境，最终通过RF模型对研究区洪水致灾范围进行精细预测。本文根据机器学习算法特性研究洪水灾害，由于洪水灾害制灾因素较多，本文选取指标不够全面，只在数据分析与算法模型方面研究，后续研究将综合更多制灾因素进行全面研究，选取更多适合洪水灾害研究的机器学习算法模型。研究主要结论如下：

1)研究区指标土壤类型重要性最高，其影响最为强烈，其次为土地利用类型、比降；降雨阈值为25、125、200 mm时，流速分类预测结果最为精确；通过RF模型与K-means算法模型对研究区流速与水位预测，降雨强度在100～175 mm时，流速变化幅度最为剧烈，降雨强度阈值达125 mm时，水位变化率最快，而降雨强度在150～175 mm之间时，水位变变化率最为明显；在ARMA模型对研究区水文参数指标回归分析中，河流比降、流量回归性拟合最好，流速、水位、河流等级变化幅度最大，且不同河段流速、水位、流量变化率与河流等级相关，等级较低径流，其水位、流速变化最为明显，而较低等级径流，流量却无显著变化。

2)机器学习能够有效拟合降雨-径流参数关系，研究区流速、水位变化主要集中于等级较高河流，而在山区，流速空间变化更为剧烈；研究区西北部、中南部流速、水位变化明显，而当降雨强度增强至125 mm时，即在暴雨、大暴雨及以上情景，径流水位变化率最为剧烈；东北部与中南部水位变化率最为明显，预测水位最高水位达20 m。