单跨双线铁路曲线桥梁车桥耦合振动特性分析
2020-02-26周海洋王宇航刘冬娅赵才友
周海洋,王宇航,刘冬娅,高 鑫,赵才友
(1.高速铁路线路工程教育部重点实验室,成都 610031; 2.西南交通大学土木工程学院,成都 610031)
轨道交通具有运量大、速度快、安全舒适等优势,在经济社会发展中发挥重要作用。但是列车通过高架桥梁时,桥梁结构会产生低频振动,由此引发相应的结构噪声。振动能量通过轨道结构传递到桥面及其他桥梁构件,并激发其振动,振动着的各桥梁构件形成一个个“声板”(由此形成噪声的“二次辐射”)[1]。高架轨道交通噪声除了轮轨噪声外,桥梁结构振动辐射的噪声已成为环境噪声的重要来源[2]。桥梁结构噪声属于低频噪声(<250 Hz),对人的身心健康会带来极大的危害[3]。特别是双线铁路曲线桥梁附近,这种现象更为复杂和严重。不同于直线桥梁,曲线桥自身结构稳定性较差,所产生的低频结构振动也较为复杂。桥梁的低频振动是产生噪声污染的主要原因,因此对曲线桥梁低频振动的研究显得尤其重要。
国内外对桥梁结构振动特性进行研究的文章比较多。例如,李宝银等[4]分析桥梁结构噪声产生的原因,提出了桥梁结构的减振降噪措施。Ngai[5]对高架桥结构共振和声共振问题进行了专门研究,并且提出了列车以140 km/h速度运行时,桥梁噪声和振动的频率范围以及共振频率。Wu[6]将轮轨相互作用力作为激励输入到桥梁结构中,并对不同形式桥梁结构振动噪声进行预测。李小珍等[7]、张迅等[8]发现了箱形桥梁结构噪声的峰值频程,在1/3倍频程中心频率50 Hz频带内存在多个振动模态,以及激振频率在50 Hz附近等。单德山等[9]提出了曲线弯梁桥的振动分析方法。易强等[10]对高架铁路环境噪声空间分布特性及控制措施效果进行了相关研究,并得出结论:无减振地段桥梁结构噪声主要集中在500 Hz以内且分别在50 Hz和250 Hz处出现最大幅值,而减振地段桥梁结构噪声主要集中在200 Hz以内且只在50 Hz处出现最大幅值。王子健等[11]对铁路混凝土箱梁的振动与噪声频谱特性进行了分析研究,认为基于底板振动加速度近似推测结构噪声的方法具有可行性,计算结果具有较高的精度,误差在5%以内,箱梁在频率60~70 Hz出现共振,并且该频率范围的声辐射效率接近最大值,二者共同导致了峰值噪声的产生。郭小敏等[12]对小半径曲线槽型梁车桥振动进行了研究,认为曲梁布置方案列车动力响应值比直梁小,桥梁曲线外侧各动力响应幅值均大于曲线内侧。王林凯等[13]采用分状态多频强迫振动方法进行主梁断面气动导数识别精度与弯扭耦合强迫振动气动导数识别精度相当,但识别效率得到明显的提升。秦佳良等[14]认为不同跨径的槽型梁结构振动与噪声的峰值频率都在63 Hz附近,最后分析得出27 m的轨道交通槽型梁的声学性能最好。另外,桥梁的振动特性还和支座及扣件等结构零件的竖向刚度有着密切的关系[15]。目前,对铁路曲线桥振动特性方面虽然有一定程度的研究,但是并不全面,对于单跨双线铁路曲线桥的研究还没有涉及。高架桥是轨道交通的主要结构形式之一,其穿越或者位于居民区,相关研究表明,列车通过高架线路的噪声通常高于地面线路的噪声,对噪声污染必须有计划、有步骤地综合治理,同时,在轨道交通的规划和设计阶段就必须合理地解决噪声问题[16]。列车通过曲线桥时,产生的振动相对于直线桥梁而言,更加复杂。易思蓉、宋郁民、时瑾等对列车通过曲线桥梁的振动特性、动力参数及振动规律做了深入研究[17-20]。随着高速铁路在世界各国的广泛修建和铁路的提速,专家学者们发现桥梁本身形式对列车过桥引起桥梁振动有着一定的影响。因此,铁路曲线桥梁车桥耦合振动及其影响分析研究具有十分重要的理论意义和工程实用价值。
1 工程概况
1.1 仿真模型的建立
在现有理论基础上,对铁路曲线梁桥车桥耦合振动进行了研究。在研究过程中,建立了曲线梁桥和直线桥梁模型,以及列车通过时的振动模型及运动方程。运用有限元软件建立了长度为32 m(单跨),桥梁宽为12 m,顶板和底板之间的间距为2.8 m的直线桥,合理地进行网格划分,与其相应的曲线桥的曲率半径为600 m。两类桥材料,结构尺寸及边界条件均相同,均是双线铁路桥梁。列车通过曲线桥梁时,分内线和外线两种仿真情况;列车通过直线桥时,仿真路线为左侧路线。在UM软件中导入建立好的柔性体桥梁模型,通过bushing力元将桥梁支座与base0基础连接。列车采用的是50个自由度的多刚体车辆模型(1节车厢),轨道采用的是无质量钢轨模型。将列车速度设置为100 km/h,仿真计算路线长度为260 m,建立曲线桥车桥耦合振动模型,并进行仿真计算,分析单跨曲线箱梁桥振动频率特性。在后处理中,提取曲线桥和直线桥顶板、底板及两侧板表面上的跨中点的加速度变量、曲线桥和直线桥顶板的位移变量、第2个轮对的横向轮轨力变量,绘制出各板件跨中位置位移-时间图像、加速度-时间图像及横向轮轨力-时间图像。通过时域对比分析曲线桥和直线桥振动特性差异,得出列车通过不同桥型时桥梁的响应程度。运用傅里叶转换将时域数据转换为频域数据,桥梁结构噪声主要是低频噪声,即小于250 Hz,所以提取0~250 Hz范围内相应的桥梁跨中位置加速度进行分析对比。通过列车通过桥梁的时域和频域分析,可以为曲线桥梁的减振降噪设计提供参考,为该类桥的车-桥耦合振动分析和工程设计提供理论参考。
1.2 有限元网格划分
在有限元软件中建立曲线桥和直线桥模型时,为了提高计算精度,减小了网格划分尺寸。划分网格是建立有限元模型的一个重要环节,它要求考虑的东西较多,需要的工作量较大,所划分的网格形式对计算精度和计算规模将产生直接影响。网格数目的多少将影响计算结果的精度和计算规模的大小。建模过程中,参考了桥梁模型划分方法,为了使计算结果精确,以及方便选取位置施加荷载,将网格尺寸设置为0.2 m×0.2 m,图1为在仿真软件中建立的模型。

图1 仿真模型
2 数据分析
2.1 时域分析
根据仿真结果,绘制出两类桥梁顶板位移-时间图像、加速度-时间图像,两类桥梁侧板和底板加速度-时间图像及列车第2个轮对左右轮横向轮轨力-时间图像等。图2是两类桥梁顶板位移-时间图像,通过对比,可以看出列车以速度100 km/h通过直线桥时对应的跨中位置最大位移为0.73 mm,通过曲线桥内线时对应的跨中位置最大位移为0.77 mm,通过曲线外线时对应的跨中位置最大位移为1.10 mm。由图2可知:相同条件下,列车通过曲线桥梁时,顶板跨中位置产生的位移较大;列车在曲线桥梁上行驶时,通过外线桥梁时跨中位置产生的位移比通过内线时更大。
图3是两类桥梁顶板加速度-时间曲线,直线桥跨中位置最大振动加速度为0.81 m/s2,曲线桥(内线)跨中位置最大振动加速度为1.31 m/s2,曲线桥(外线)跨中位置最大振动加速度为3.23 m/s2。由此可知,列车通过时,曲线桥产生的振动更大,特别是列车经过曲线桥外线时,顶板跨中位置产生的振动更大。

图2 直线桥和曲线桥(内线和外线)顶板位移-时间曲线(跨中)
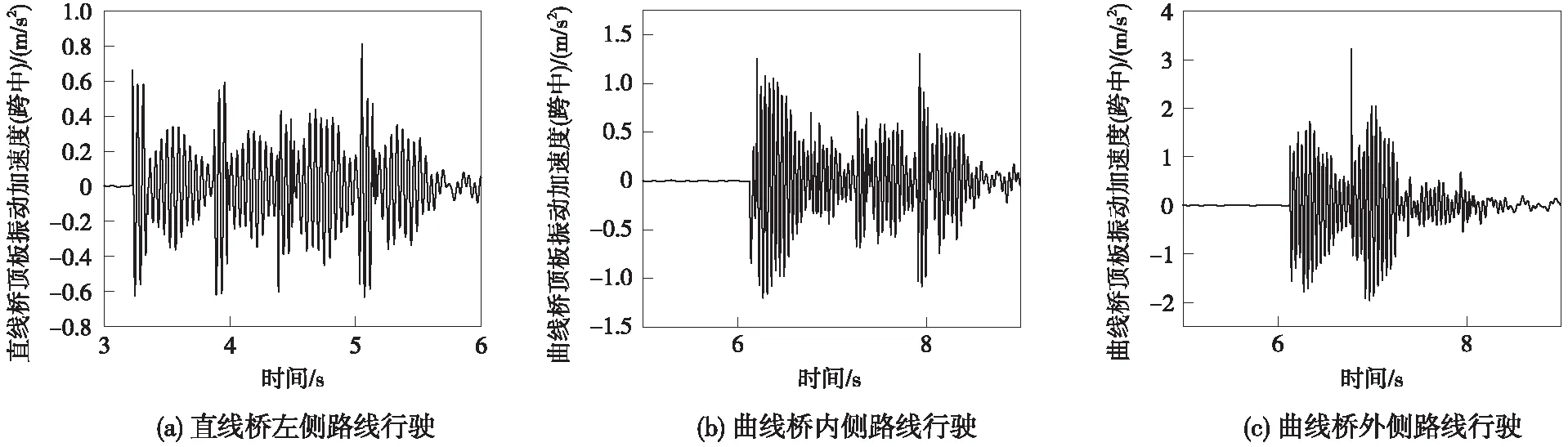
图3 直线桥和曲线桥(内线和外线)顶板振动加速度-时间曲线(跨中)
通过直线桥时,列车行驶路线为左侧路线。由图4、图5可知,直线桥左侧板跨中位置最大振动加速度为0.42 m/s2,右侧板跨中位置最大振动加速度为0.30 m/s2。由于列车在桥梁左侧路线上行驶,所以左侧板跨中位置最大振动加速度比右侧板跨中位置最大振动加速度大。列车通过曲线桥内线时,左侧板跨中位置最大振动加速度为1.91 m/s2,右侧板跨中位置最大振动加速度为1.23 m/s2。与直线桥侧板振动对比,可知曲线桥的振动更大。列车通过曲线桥外侧时,左、右侧板对应跨中位置振动加速度分别1.18,1.19 m/s2。由此可知,列车走外线时,相比内线,曲线桥侧板振动更小。
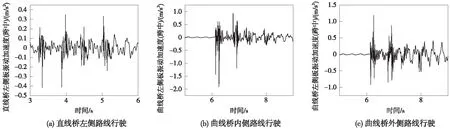
图4 直线桥和曲线桥(内线和外线)左侧板振动加速度-时间曲线(跨中)
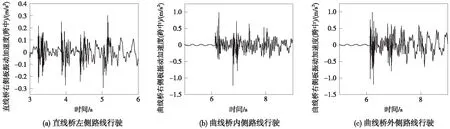
图5 直线桥和曲线桥(内线和外线)右侧板振动加速度-时间曲线(跨中)
图6是直线桥和曲线桥(内线和外线)底板振动加速度-时间曲线。直线底板跨中位置振动加速度为0.27 m/s2,曲线桥(内线行驶)底板跨中振动加速度为1.18 m/s2,曲线桥(外线行驶)底板跨中位置振动加速度为1.08 m/s2。可知曲线桥底板振动相比直线桥更大,列车走外线时,相比内线,曲线桥底板振动更小。

图6 直线桥和曲线桥(内线和外线)底板振动加速度-时间曲线(跨中)
2.2 频域分析
通过傅里叶转换后,得到曲线桥和直线桥顶板、底板及左右侧板跨中位置振动加速度与频率(0~250 Hz)的关系。由图7可知,列车通过两种桥梁时,顶板的垂向振动加速度都是在频率21~240 Hz范围内达到最大,3种工况的振动加速度峰值都出现在225 Hz附近。两种桥梁顶板垂向振动加速度所对应的主频都是两个,直线桥顶板峰值振动加速度的主频分别是219 Hz和225 Hz,对应的振动加速度分别是0.086 m/s2和0.097 m/s2;曲线桥(内线行驶)顶板峰值振动加速度的主频分别是219 Hz和235 Hz,对应的振动加速度分别是0.059 m/s2和0.061 m/s2;曲线桥(外线行驶)顶板峰值振动加速度的主频分别是223 Hz和235 Hz,对应的振动加速度分别是0.090 m/s2和0.140 m/s2。由此可以得出结论,无论直线单跨桥梁,还是曲线单跨桥梁,顶板振动加速度都有两个主频,分布在210~240 Hz范围内。在低频范围内,曲线桥(内线行驶)顶板峰值振动加速度比直线桥顶板峰值振动加速度小,曲线桥(外线行驶)顶板峰值振动加速度比直线桥顶板峰值振动加速度大。通过图像走势及峰值分析,曲线桥产生的低频振动更大。
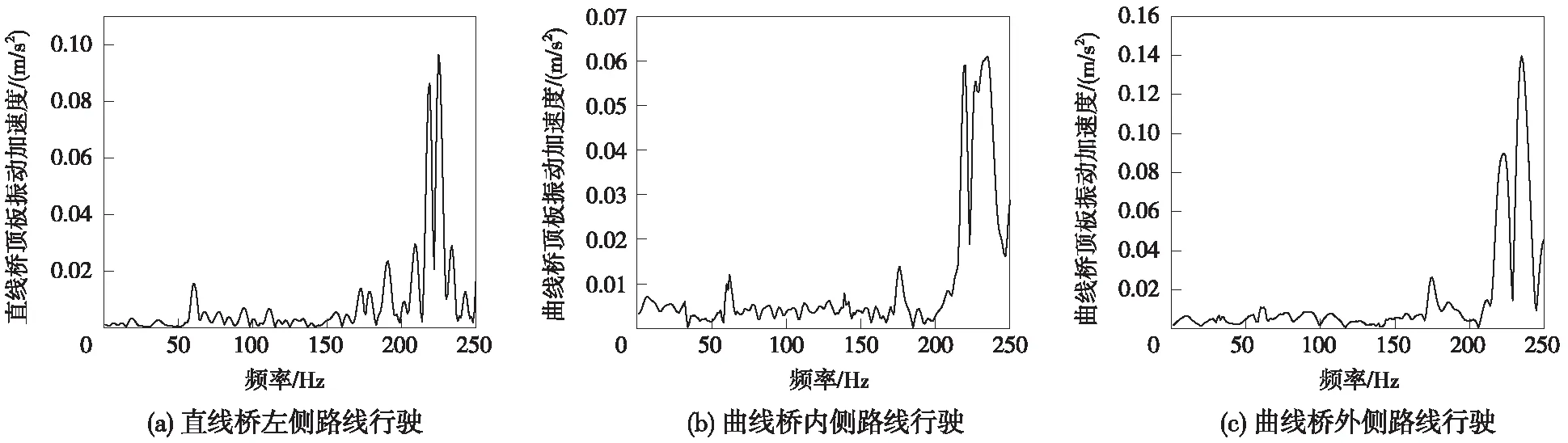
图7 直线桥和曲线桥(内线和外线)顶板振动加速度-频率曲线(跨中)
由图8可知,列车通过直线桥时,左侧板振动加速度在32,60,131,190 Hz达到峰值,分别是0.017,0.015,0.015,0.017 m/s2,直线桥左侧板振动加速度对应4个主频。列车通过曲线桥内侧线路时,左侧板振动加速度在34,62,129,188 Hz达到峰值,分别是0.012,0.010,0.015,0.014 m/s2,曲线桥(内线行驶)左侧板振动加速度对应4个主频。列车通过曲线桥外侧线路时,左侧板振动加速度在31,62,235 Hz达到峰值,分别是0.025,0.012,0.014 m/s2,曲线桥(外线行驶)左侧板振动加速度对应3个主频。因此,直线桥和曲线桥(内线行驶)左侧板振动加速度主频分布在30,60,130,190 Hz附近,而曲线桥(外线行驶)左侧板振动加速度主频分布在30,60,235 Hz附近,对应的加速度对桥梁结构低频噪声的产生起着主要作用。通过图像走势及峰值分析,可知列车通过曲线桥时,相比直线桥,左侧板产生的低频振动更大。

图8 直线桥和曲线桥(内线和外线)左侧板振动加速度-频率曲线(跨中)

图9 直线桥和曲线桥(内线和外线)右侧板振动加速度-频率曲线(跨中)
由图9可知,列车通过直线桥时,右左侧板振动加速度在31,61,130,191 Hz达到峰值,分别是0.015,0.013,0.015,0.010 m/s2,对应4个主频。列车通过曲线桥内侧线路时,右侧板振动加速度在33,59,128,173,187 Hz达到峰值,分别是0.019,0.011,0.017,0.015,0.011 m/s2,曲线桥(内线行驶)左侧板振动加速度对应5个主频。列车通过曲线桥外侧线路时,右侧板振动加速度在32,174,235 Hz达到峰值,分别是0.035,0.028,0.015 m/s2,曲线桥(外线行驶)右侧板振动加速度对应3个主频。因此,直线桥和曲线桥(内线行驶)右侧板振动加速度主频主要分布在30,60,130,190 Hz附近,曲线桥(内线行驶)右侧板对应主频还分布在175 Hz附近。而曲线桥(外线行驶)右侧板振动加速度主频分布在30,175,235 Hz附近,对应的加速度对桥梁结构低频噪声的产生起着主要作用。通过图像走势及峰值分析,可知列车通过曲线桥时,相比直线桥,右侧板产生的低频振动更大。
图10为两类桥梁在三种工况下底板跨中位置振动加速度-频率曲线,列车通过直线桥时,底板振动加速度在61,208,218 Hz达到峰值,分别是0.015,0.017,0.017 m/s2,直线桥底板振动加速度对应3个主频。列车通过曲线桥内侧线路时,底板振动加速度在63,175,219 Hz达到峰值,分别是0.009,0.010,0.011 m/s2,曲线桥(内线行驶)底板振动加速度对应3个主频。列车通过曲线桥外侧线路时,底板振动加速度在59,173,219 Hz达到峰值,分别是0.011,0.017,0.014 m/s2,曲线桥(外线行驶)底板振动加速度对应3个主频。因此,曲线桥(内线行驶)和曲线桥(外线行驶)底板振动加速度的主频都是在60,175,220 Hz附近,而直线桥底板振动加速度的主频是在60,210,220 Hz附近。通过图像走势及峰值分析,可知列车通过曲线桥时,相比直线桥,底板板产生的低频振动更大。

图10 直线桥和曲线桥(内线和外线)底板振动加速度-频率曲线(跨中)
2.3 模态分析
由前面的时域和频域分析可知,单跨双线曲线桥振动大于单跨双线直线桥。探究曲线桥低频振动比直线桥较大的原因,发现在235 Hz附近,曲线桥(内线和外线)顶板振动发生了较大的振动,而直线桥顶板振动较小。列车在外线行驶时,左右侧板在175,235 Hz附近对应的振动加速度较大,而在曲线桥内线和直线桥上行驶时,左右侧板振动受该频率影响不大。曲线桥(内线和外线)底板振动加速影响最大的主频是175 Hz,而直线桥底板振动加速度受影响较小。在有限元软件中,运用分块兰索斯法提取曲线桥模态。根据实际需要,提取了175 Hz和235 Hz及附近频率对应的振型。图11从左往右分别为172.95,174.71,176.03 Hz对应的振型,图12从左往右分别为234.5,235 Hz对应的振型。
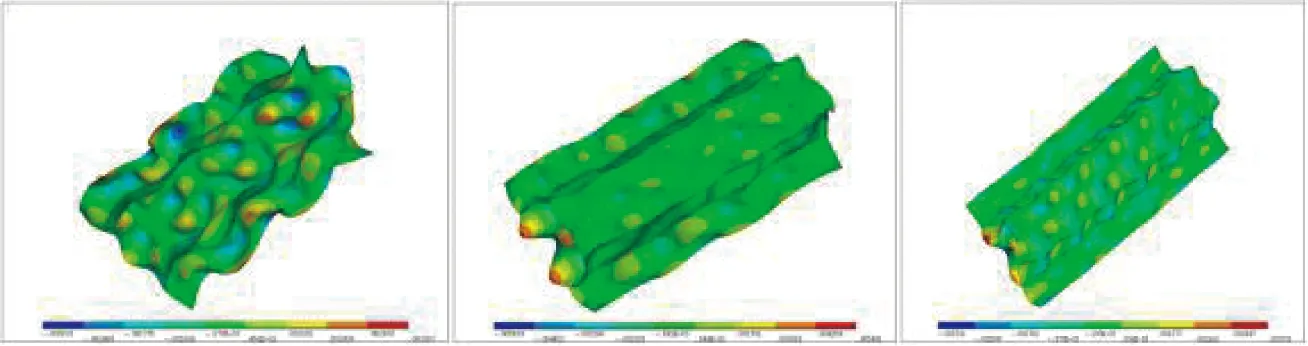
图11 曲线桥振型(175 Hz附近)
由图11、图12可知,曲线桥侧板振动相比直线桥较大的原因是由于桥梁侧板在175 Hz附近发生了横向振动,在235 Hz附近发生了较大的垂向振动。曲线桥底板在175Hz附近还发生了较大的垂向振动,导致底板相比直线桥产生了较大的振动。由图12可以很清晰地看出,235 Hz附近的垂向振动同样对曲线桥顶板产生了很大的影响。
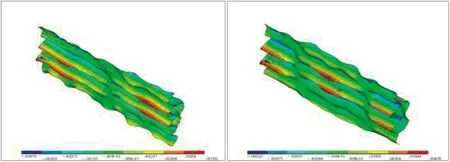
图12 曲线桥振型(235 Hz附近)
3 结论
当列车以100 km/h行驶通过两种单跨双线桥梁(共3种工况)时,根据所得到的数据进行时域、频域及模态分析。主要结论如下。
(1)相同条件下,顶板跨中结构位移方面,曲线桥(外线行驶)>曲线桥(内线行驶)>直线桥。顶板振动加速度方面,曲线桥(外线行驶)>曲线桥(内线行驶)>直线桥。但是在两侧板、底板振动加速度方面,曲线桥(内线行驶)>曲线桥(外线行驶)>直线桥。
(2)由于向心力的影响,桥梁会受到较大的横向力,这对桥梁的结构稳定性会产生一定的影响。通过时域、频域及模态分析可知,相同条件下,曲线桥振动大于直线桥的主要原因:在175 Hz附近左右侧板和底板分别产生了较大横向振动和垂向振动,在235 Hz附近侧板和顶板产生了较大垂向振动。
(3)相同条件下,曲线桥相比直线桥振动更大、更复杂,产生的低频结构噪声也更大。在解决双线曲线桥结构噪声问题时,一方面可以使用减振材料,另一方面可以加强曲线桥梁自身的结构稳定性。
