基于细观尺度粗糙轮轨接触蠕滑特性数值分析
2020-02-26周成博马道林
周成博,马道林
(1.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031; 2.西南交通大学土木工程学院,成都 610031)
1 研究背景
轮轨黏着规律是轮轨关系研究的核心基础。18世纪末Carter[1]首先解决了二维弹性体滚动接触问题。他利用库伦摩擦定律和Hertz接触理论成功地计算出接触斑内切向应力的大小,划分出了黏着区和滑动区,为轮轨黏着的研究奠定了理论基础。Vermulen和Johnson[2]则将Carter理论扩展到三维无自旋椭圆接触。在此基础上Kalker[3]建立了至今为主应用最为广泛的由线性理论、简化理论和精确理论组成的蠕滑理论。
以上涉及的都是不考虑轮轨表面粗糙度则在且向上均采用库伦摩擦模型即摩擦系数恒定不变的算法。为了更为真实地模拟轮轨接触,一些学者考虑使用函数型摩擦系数代替库伦摩擦,如Polach[4]在其模型中引入速度型摩擦函数以考虑轮轨接触剪切刚度;张卫华等[5]将速度型摩擦系数引入FASTSIM算法中,常崇义[6]利用ABAQUS软件建立稳态轮轨滚动接触有限元模型,其中摩擦系数随着轮轨微滑速度变化。
以上方法考虑到了摩擦系数随速度的变大,但仍将车轮与钢轨表面视作光滑表面,导致计算结果与现场试验不同。因此一些学者开始考虑将轮轨表面视作粗糙表面来进行接触计算。孙琼[7]基于GreenWood的粗糙表面弹性接触模型,改良后得到粗糙表面的弹-塑性接触模型,进行粗糙轮轨表面的接触计算;吴兵等[8]则通过数值模拟的方法计算了水油等第三介质存在下的轮轨粗糙表面接触计算。以上计算仍基于Greenwood[9]对于粗糙度的计算方法,从统计学的角度出发,缺乏物理本构模型的支持。
本文尝试从物理学的角度出发,旨在研究干燥条件下中尺度的轨道接触,以较小规模且随机的方式理解轮轨摩擦行为。Braun[10]引入中尺度摩擦模型来解释摩擦的起始,即摩擦从黏着到滑动的过渡。Braun的模型[10]解释了很多关于黏滑过渡的实验结果,这些结果是在高于10 000 frames/s的采样率下用高速摄像机获得的[11-13]。而轮轨接触斑内滑动区与黏着区的存在,则使得与上述论文中类似的方法来模拟轮轨接触提供了理论基础,不仅能考虑滑动而且能考虑滚动。Aghababaei[14]对从接触到两个粗糙表面之间的粗糙度分离的整个过程的数值研究与分子动力学模拟证实了模拟摩擦接触有效性,并揭示了其中涉及的许多细节。与基于库仑摩擦和理想光滑接触几何形状的传统轮轨接触模型相比,本模型描述了微米尺寸的粗糙表面的摩擦相互作用。更具体地说,该模型通过模拟轨道和车轮之间每个微凸体接触对的生命周期来模拟摩擦接触:从建立接触到拉伸,完全接触,到最后断开并在短暂的休息时间后重新建立。它不仅可以描述轮轨接触的纵向蠕变效应,还可以揭示滑动速度对轮轨接触摩擦性能的影响。
该研究所提出的模型,在滚动和滑动共同作用下,深刻地表征了轮轨接触行为并揭示了摩擦演变的机制,这对于理解轮轨的动态接触过程十分重要。
2 轮轨黏着力模型
采用的二维轮轨黏着力动态计算模型是基于Matlab程序设计的数值计算模型。考虑到粗糙度对轮轨接触的影响,模型中利用微凸体之间的接触来模拟轮轨间的蠕滑力。由于仅考虑纵向蠕滑,根据对称性模型简化为单轮单轨之间的接触。
2.1 粗糙度的模拟
微观尺度上,轮轨表面并非绝对光滑,而是有很多被称为微凸体的不规则粗糙峰存在。两个粗糙物体的接触实质上是微凸体之间的接触,会导致真实接触面积远小于名义接触面积。在力学中,往往将两个粗糙表面之间的接触简化为光滑表面和粗糙表面的接触,故本文将轮轨接触模拟为光滑车轮和粗糙钢轨的接触。结合Daves[15]等人实测的轮轨表面粗糙度的数据,假设轮轨表面的微凸体高度值的分布服从Gaussian分布,可以随机生成一系列的微凸体数据,如图1所示。

图1 轮轨表面接触示意
在数值模拟的过程中,在椭圆形的接触内随机产生各个大小不等互不相交的圆来模拟微凸体之间的接触。在本模型中,利用Matlab程序产生系列的微凸体,图2即为数值模拟示意。图中每个小圆代表一对相互接触的微凸体接触对,两两之间互不影响。因此在粗糙度的模拟中,微凸体的高度hi与半径ri的关系为正比,即hi∝ri。两个物体接触时的轮廓接触面积占名义接触面积的5%~15%,根据这个比值可以大致确定接触斑内需要生成的微凸体接触对的数量。图2是通过Matlab程序在椭圆接触内随机产生微凸体接触圆的数值模拟结果。图中的椭圆为接触斑的轮廓,椭圆内的小圆则代表着微凸体接触对。
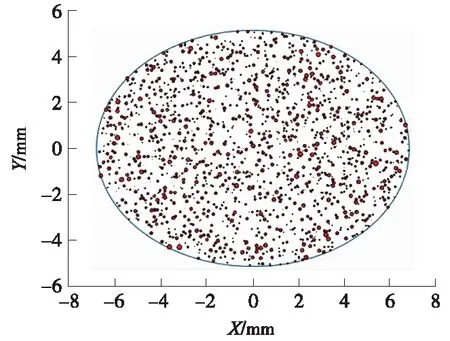
图2 接触斑微凸体接触的数值模拟
2.2 接触模拟
2.2.1 垂向接触
将轮轨表面视作光滑的椭球面,利用Hertz接触理论计算出接触斑的几何形状和接触内的垂向应力分布,如图3所示,具体公式如下

(1)

(2)
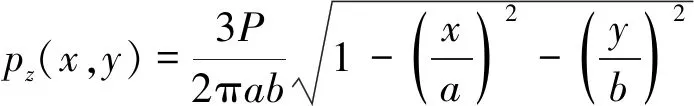
(3)
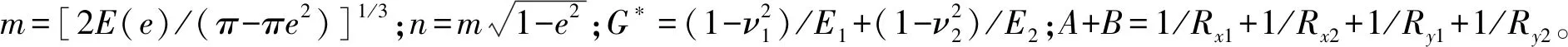
式中,a、b分别为椭圆接触斑的长短轴长度;P为单轮的轴重;pz(x,y)为接触斑内法向接触应力的分布;Rx1,Rx2,Ry1,Ry2分别为车轮和钢轨接触点处横纵向曲率半径;E(e),e为椭圆积分参数。
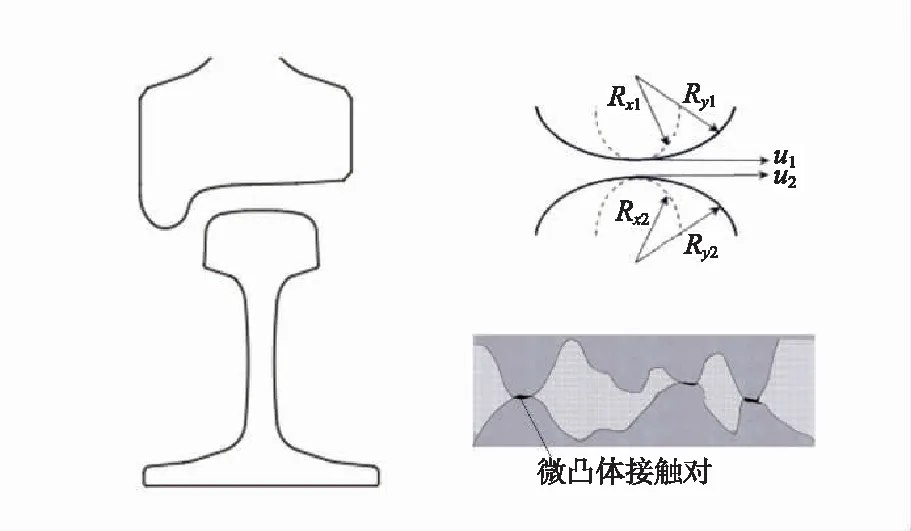
图3 轮轨垂向接触示意
由于Hertz接触计算的是无摩擦的光滑表面,而数值模拟中需要考虑到粗糙度,因此需要对法向应力的数值进行一定的修正,修正公式可表述为
H×(∑∂i×si)=P
(4)
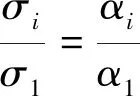
(5)
式中,αi为微凸体的受压程度;si为微凸体完全接触时受压面积(即小圆面积);H为材料硬度;P为单轮轴重。
σi为小圆中心处的压应力,由于ri≪a(b),可用小圆中心处的垂向应力表示整个小圆上的平均应力。
在不存在第三介质(干摩擦)的情况下,轮轨相互作用的力全部由微凸体之间的接触来传递。轮轨接触时,并不是所有的微凸体之间都能达到预设的最大接触面积,小圆面积si乘上受压系数αi即表示当前时刻的受压面积。
2.2.2 切向接触
切向接触的模拟是本模型的重点,着重于从物理本构的角度来描述摩擦。因此暂时只考虑纵向蠕滑率,只考虑单轮在单轨上的运动,简化为椭圆接触斑在生成的粗糙表面上移动。接触斑的移动速度与车轮的行进速度v0相同,车轮的微滑速度v1则使得弹簧拉伸来模拟蠕滑力。在微凸体相互接触时,会经历两个微凸体从相互接近到接触,接触面积逐渐到最大值之后接触对逐渐分离的过程。半径越大的微凸体在接触时越难产生相对位移,即用来模拟接触的弹簧上升刚度k1越大,即k1∝hi。在微凸体完全接触(即弹簧到达受力极限)后,会在此状态维持一段时间再开始分离,Ramin Aghababaei[14]利用离散元的方法模拟了整个微凸体从接触到分离的全过程,为了简化模型用线性弹簧来模拟整个受力过程。每个弹簧受力极限的确定公式可表述为
fi=μ·αi·si·H
(6)
式中,μ为垂向力和切向力的相关系数,在低速(微滑)的情况下,摩擦力仍与压力呈正比。文献[16]通过一系列的实验确定了微凸体处于边界润滑时的摩擦系数,一般在0.2~0.4。当模拟工况为干摩擦时,的取值可参考文献[17],一般为0.53~0.63。
图4为单个弹簧的受力,两个微凸体从开始接触到完全接触这一个阶段,即弹簧拉力上升的阶段。随着滑动量的增大,微凸体接触对之间的接触面积随之变大,切向力也随着线性增大,直至两个微凸体完全接触。之后随着车轮继续滑动,微凸体接触对开始分离,这时最大切向力会有一个短暂的稳定期。随着微凸体接触对的分离,接触力逐渐变小,直至完全分离。基于Ramin Aghababaei的仿真数据和轮轨表面微凸体的几何参数,微凸体分离时力的减小,假设弹簧下降段的刚度k2与k1正相关,k2∝k1。完全分离后的微凸体再次接触之前会经历一个时间来恢复形变。从物理学的角度来看,两个微凸体从相互分离到重新接触,必然会经过一个时间Δt。O.M.Barun的摩擦模型则验证了Δt对描述摩擦的重要性以及物理意义,尤其是从静摩擦到动摩擦的变化阶段,这与接触斑内黏着区到滑动区的过度有着极高的相似性。
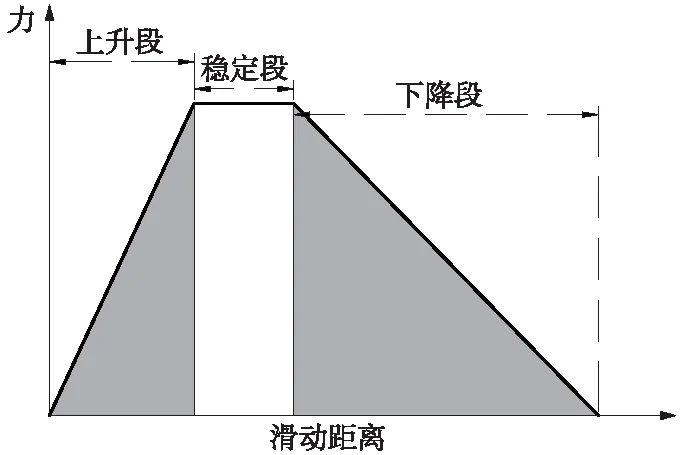
图4 弹簧受力示意
当前时刻的纵向蠕滑力即为接触斑内所有弹簧力的总和。在不同的时间步长内,每个微凸体接触对在接触斑内的位置发生改变,随之而改变的是微凸体的法向受力,进一步影响弹簧的受力极限fi,而不是严格如图4所示,峰值会维持在一个恒定值。
2.3 模型概述
数值模拟利用MATLAB程序设计计算,计算流程如图5所示。模型首先输入车轮和钢轨的参数,利用Hertz接触理论算出单轮单轨工况下接触斑的几何参数和垂向应力分布,经过粗糙度修正之后利用弹簧摩擦模型进行切向接触模拟。
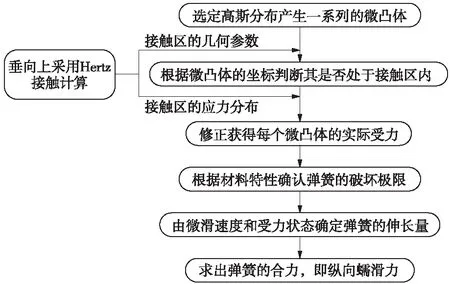
图5 计算流程
3 结果分析
本文将通过模型所计算的牵引系数与蠕滑率的关系与试验和线路测试的结果相比较,来验证模型的正确性。本节将讨论列车速度、纵向蠕滑率和粗糙度参数等因素对黏着系数的影响以及接触斑内滑动区和黏着区的分布。
3.1 模型的验证
模型现阶段主要是对干摩擦的模拟,考虑到对滚机难以模拟高速下的轮轨,现场所测得的高速列车数据也较少,故模型验证选取中低速工况。图6分别展示了列车速度为36 km/h[18]和60 km/h[19]时,仿真结果与现场测试以及对滚机实验结果的对比,工况均为干摩擦。从图6可以看出,数值模拟的结果与实测数据吻合程度很高。牵引系数与蠕滑率的曲线在小蠕滑时呈线性上升,达到峰值之后有一个下降的过程。

图6 牵引系数-纵向蠕滑率曲线
表1显示了模型在数值计算中使用的模拟参数。对于表格中尚未列出的参数如微凸体的最大静摩擦系数则根据实际工况选取。
3.2 速度与蠕滑率
随着高速铁路的普及,而速度与蠕滑率对牵引系数影响非常大,因此研究牵引系数与之的关系十分重要。图7展示了干摩擦工况下滚动速度、蠕滑率与牵引系数的关系。随着速度的增加,黏着系数逐渐减小,这一结果符合现阶段的认识。随着滚动速度的增大(接触斑移动速度的增加),在相同的时间内,微凸体之间的相对位移更小,也即弹簧的拉伸量变小,蠕滑力因此变小。

表1 计算参数

图7 牵引系数-速度-蠕滑率曲线
而在速度一定时,随着蠕滑率的增大,牵引系数先增加后减小,与Kalker的接触理论的计算结果相比,多出了之后的下降段。主要原因是后者在计算蠕滑力时,摩擦系数是一个常数,未考虑到动摩擦系数会随着速度的增加而减小的现象。在速度一定时,随着蠕滑率的变大,在相同的时间内,弹簧的拉伸量变大。在弹簧的受力达到极限值之前,随着拉伸量的增大,弹簧受力也变大,反映出牵引系数随蠕滑率的变大而变大的规律,直至接触斑到达完全滑动的状态。当纵向蠕滑率继续增大时,切向接触弹簧将会逐渐拉伸至弹簧的破坏极限值,即每个微凸体的接触对开始分离,弹簧所表示的切向力开始下降,揭示了牵引系数-纵向蠕滑率曲线中下降段的原因。
3.3 粗糙度参数
轮轨表面由于加工等因素会不可避免地产生凹凸不平的微凸体。一般而言,表面粗糙度的关键参数主要是微凸体高度的均值和标准差即分布。本小节主要讨论不同微凸体高度均值和标准差与均值之比对轮轨黏着特性的影响。
图8为干摩擦工况下牵引系数随着微凸体高度均值变化的曲线。从图8可以看出,黏着系数是随微凸体均值的增加而变大的。这种趋势解释了通过合理撒砂提高轮轨黏着系数的现象,结论和日本忠夫[20]试验所测得的变化趋势不一致,可能是由于湿摩擦时,随着微凸体高度均值变大,接触的微凸体总面积变小,而介质承担更多的接触力导致黏着系数变小;干摩擦下仍由微凸体承担全部的接触力故未有变小的趋势。
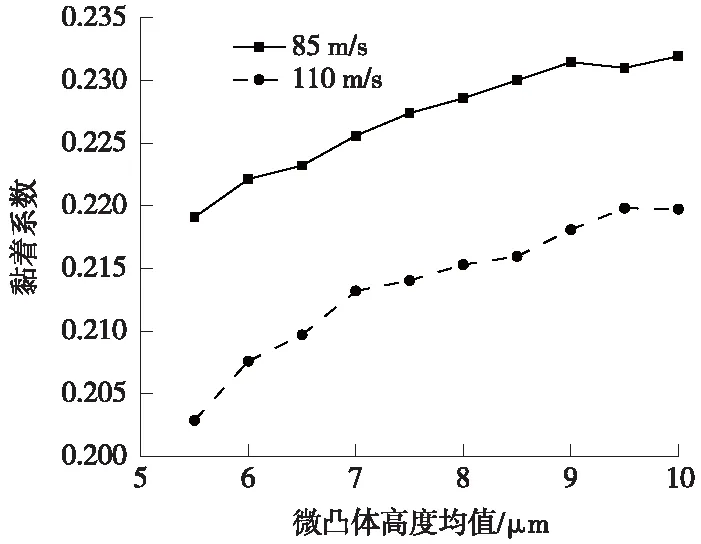
图8 微凸起高度值均值-黏着系数曲线
由图9可以看出,牵引系数随着粗糙度分布的高度均值与标准偏差之比的增大而变大。在实际情况中,h/σ不会无限度的变大,具体取值可根据实地测量的轮轨粗糙度数值来确定。
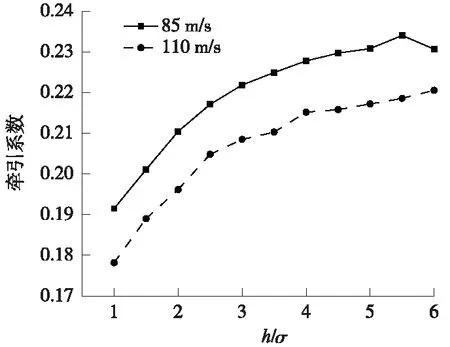
图9 标准差与高度均值之比-牵引系数曲线
轮轨间的黏着系数随着表面粗糙度高度均值变大的主要原因是:随着微凸体高度均值的增大,接触区的相互接触的微凸体由更多更小向更少更大转变,即微凸体接触对完全接触时的接触力更大,这可能是导致微凸体高度均值增大时,牵引系数也随之增大的主要原因。从图8也可以看出,在同一粗糙度下,车轮的滚动速度越大黏着系数越小,这种现象与3.2节中的结论一致。由此可见,某种程度上粗糙度是增加轮轨黏着系数的有利因素。在车轮踏面和钢轨轮廓的设计和维护中,如果适当的控制表面粗糙度,有利于改善黏着能力。
3.4 摩擦系数
与传统的轮轨力计算模型不同的是,模型中并未定义动摩擦系数,也未在计算中直接在接触斑内划分滑动区和黏着区。模型通过计算接触斑内每个单元的牵引系数来划分滑动区和黏着区。如图10所示,在滚动速度为360 km/h时,随着纵向蠕滑率的增大,接触斑内各个单元的牵引系数变化趋势较为明显。黄色的部分代表当前单元的牵引系数近乎于最大值,即该单元内的切向弹簧受力近似于最大值。在纵向蠕滑率小于0.6%时,达到最大牵引系数的单元由接触斑末端向中心处逐渐增多。若划定接触斑内的滑动区与黏着区,切向弹簧受力达到极限则微凸体的接触对开始相对滑动,故可将牵引系数近似最大值的单元当作滑动区。当纵向蠕滑率继续增大时,黄色单元会继续向接触斑前缘移动,滑动区的范围进一步扩大。同时由于接触斑末端的接触对开始相对滑动,切向弹簧受力值降低,导致接触斑末端的单元牵引系数降低,但这些单元仍处在滑动区。

图10 不同蠕滑率下的牵引系数分布
图11是列车速度为360 km/h,纵向蠕滑率为0.8%时的牵引系数曲线。从图11可以看出,牵引系数在接触区前缘有一个线性增长的过程,对应黏着区的摩擦系数是逐渐变大的,达到峰值时即为统计学上的最大静摩擦系数,进入到滑动区。牵引系数的骤降段是从最大静摩擦系数到动摩擦系数的减小过程。在滑动区牵引系数继续下降是由于微凸体接触对开始相对滑动,切向接触力逐渐减小。
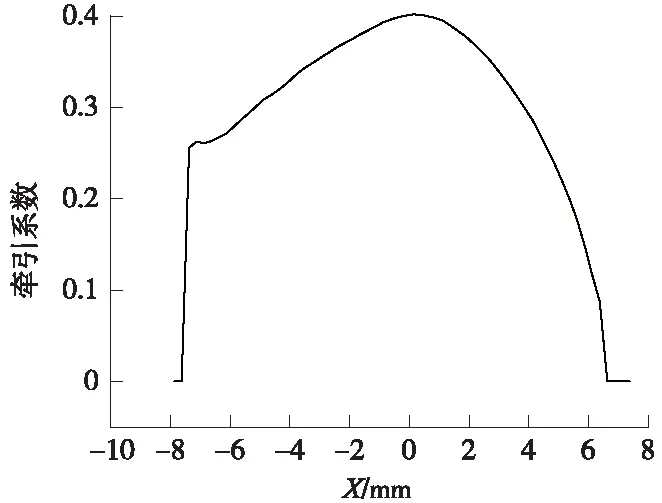
图11 牵引系数曲线(v=360 km/h,纵向蠕滑率ξ=0.8%,x轴正方向为列车前进方向)
将牵引系数的峰值定义为本模型中的摩擦系数,可得切向力与垂向力乘摩擦系数的对比图,如图12所示。与传统的蠕滑模型所不同的是,本模型采用的摩擦系数即非动摩擦系数,也非静摩擦系数,而是通过统计学得到的一个平均静摩擦系数,其值小于最大静摩擦系数,大于动摩擦系数。由图12的对称性来看,此工况下接触斑内应处于全滑动状态,与图10中纵向蠕滑率为0.8%的结果对应,图中蓝色部分表示该单元内此时刻没有接触体处于接触状态,接触斑前缘有少量单元的牵引系数并未达到最大值,从统计学的角度来看该单元内的大部分微凸体接触对已经滑动至接触分离的状态。
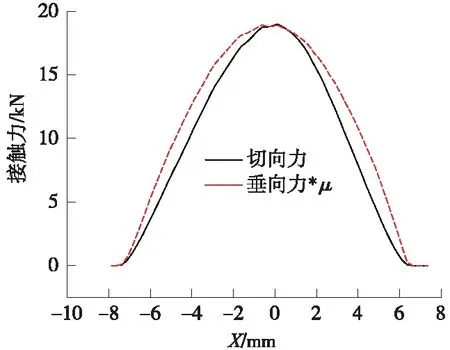
图12 接触力对比曲线(x轴正方向为列车前进方向)
4 结论与展望
本文介绍一种中尺度动态轮/轨接触模型,通过该模型,研究了影响牵引系数的轮轨速度,蠕变速率和粗糙度等因素。在分析数值计算结果之后,得到以下结论。
(1)当考虑到粗糙度的影响时,接触应力的最大值比光滑表面的计算结果要大,且曲面不平滑存在着许多小锯齿。
(2)随着轮轨表面的微凸体高度值的增大,高速情况下的轮轨黏着系数变大。
(3)模型的计算结果与试验数据吻合良好,验证了数值计算模型和算法的可行性。这表明该模型虽然被设计为动态模型,但仍能够预测稳态牵引因子。
(4)模型中并未人为地划定滑动区与黏着区,而是通过整个接触斑内各个单元牵引系数的变化,刻画出滑动区到黏着区过渡的整个变化过程。
在以后的研究中会将模型从二维拓展到三维,进一步考虑到横向蠕滑和自旋蠕滑的影响,并进行高速下的模型验证。
