基于子图特征的科学家合作网络链路预测

许 爽，李淼磊

(大连民族大学 信息与通信工程学院，辽宁 大连 116605)

在知识经济时代，合作关系隐含着知识在某种社会关系之间的交流、转移、共享[1]。科学家合作网络是以论文作者为中心的一种社会网络，其中论文作者是网络中的节点，论文作者之间的合作关系是网络的连边。科学家合作网络会随时间推移而演化， 目前学者们主要是从网络结构、网络演化机制、网络增长及个人合作行为上研究科学家合作网络。

由于链路预测在复杂网络研究中具有重要价值。因此，对链路预测方法以及提高预测准确率的研究也自然成为了重点。在链路预测中，准确率取决于网络中提取的相似性特征是否能够很好的反映出给定网络的拓扑结构，而相似性特征的优劣则可以通过特征选择方法来评价。特征选择是指从原始特征集中选择出能使某种评价特征最优的特征子集[2]。在链路预测方法研究中，把链路预测与特征选择相结合，从而形成一种新的研究思路，对预测结果和相似性特征进行进一步探究，对于分析不同相似性特征与网络结构的关系具有重要意义。

网络科学领域中研究链路预测的方法主要可以分为基于极大似然和概率模型的方法、基于机器学习的方法、基于网络表示学习的方法、基于相似性的方法[3]；Clauset[4]等人提出了基于网络层次的最大似然估计模型，该算法在层次结构比较显著的网络中预测效果良好；Fire等[5]利用机器学习中的支持向量机、决策树和人工神经网络对网络中缺失的连边进行预测；Pachaury[6]等人提出了一种基于拓扑特征和集合模型的链路预测方法，从网络图中提取拓扑特征，用于训练随机森林分类器模型，并在两个公开数据集上进行验证；贾承丰[7]等人将深度学习特征提取算法和优化问题中的粒子群算法相结合，提出了一种基于词向量的粒子群优化算法(word2vec-POS)。

基于相似性的方法，尤其是基于网络拓扑结构相似性的方法，由于算法简便、复杂度低，受到了广泛关注[8]。每种相似性方法包含不同的相似性特征，如共同邻居特征[9]、Katz特征[10]、SimRank特征[11]分别属于基于局部信息、基于路径和基于随机游走的相似性特征。

基于网络拓扑结构的相似性定义方法是由Liben-Nowell和Kleinberg[12]提出的，同时他们还发现在大型科学家合作网中，使用节点共同邻居和Adamic-Adar特征(Adamic-Adar Index，AA)的准确率最高。周涛等人[13]证实了Liben-Nowell和Kleinberg的研究结果，并在此基础上提出了资源分配特征(Resource Allocation Index，RA)和局部路径特征(Local Path Index，LP)。在最近的研究中，王凯[14]等人定义了节点间资源承载度相似性特征QN，并提出相应的链路预测方法。通过实验证明，相比于其他方法，该方法拥有较高精度。路兰[15]等人提出一种基于试验设计的链路预测算法，将三个预测精度高的传统相似性特征相加，并通过均匀配方试验设计法给相似性特征赋予权重，构建混合相似性特征，从而应用于链路预测中。Kumar[16]等人提出基于二级节点聚类系数的链路预测方法，该方法定义了二级公共节点及其聚类系数的概念，并基于该信息计算节点相似性。目前，基于网络拓扑结构相似性链路预测方法的研究中，存在如下问题：(1) 相似性特征类别固定且数量较少;(2)独立的相似性特征无法全面反映网络演化的多样性和复杂性，对众多相似性特征之间的协作关系和同类别相似性特征的影响力无法具体分析。

目前关于特征选择方法的研究主要分为过滤法(Filter)、封装法(Wrapper)和嵌入法(Embedded)[17]。过滤法的应用非常普遍，其关键就是找到一种能度量特征重要性的方法，比如Pearson相关系数[18]、最大信息压缩指数[19]、信息增益、互信息及最大信息系数[20]等。很多研究者在进行特征选择时对上述方法进行了改进或提出了新的度量方法。张海洋[21]在持股集中度与股票价格关系的研究中应用了最大信息数的特征选择方法。孙广路等人[22]提出了基于最大信息数和近似马尔科夫毯的两阶段特征选择方法，分别对特征的相关性和冗余性进行分析，得到了很好的效果。在封装法中，对于一个待评价的特征子集，需要训练一个分类器，根据分类器的性能对该特征子集进行评价。封装法中用以评价特征的学习方法是多种多样的，例如决策树、神经网路、近邻法以及支持向量机等[23]机器学习方法。关于封装法的研究中， Hancer[24]等人提出一种基于人工蜂群优化的特征选择方法，并使用KNN分类算法选择最优特征子集。Wei[25]等人提出一种基于记忆更新和增强变异机制的BPSO-SVM算法，对标准二进制粒子群优化算法(BPSO)进行改进，且采用SVM模型作为特征评估部分，实验结果表明，该算法具有较高的精度。嵌入法将特征选择过程与机器学习模型相结合，其特征选择精度主要依赖于选取的特征选择方法和分类模型。有关嵌入法的研究中，傅昊[26]等人提出基于随机森林和RFE的组合特征选择方法，分别采取随机森林算法和SVM-RFE算法，将得到的两个特征子集进行综合，得到最终的最优子集，然后使用SVM模型对入侵检测系统中的未知样本进行预测。

综上所述，本文提出了多类别网络结构的链路预测方法，将网络结构特征分为五类特征，分别是基于节点度和中心性相似性特征、基于节点和边的共同邻居相似性特征以及基于邻居和边的子图相似性特征。先计算网络中同类别特征统计量，即特征工程的建立，然后计算各个特征统计量的影响力和相互关系，即进行特征选择，最后通过有监督的二分类机器学习算法实现链路预测。衡量链路预测方法的好坏，最终要通过评价标准来实现。研究结果表明，基于子图的相似性特征在科学家合作网络中具有最好的预测效果；此外，研究中分析并选择合适的特征选择方法，通过选取最优子集来揭示特征统计量类内相互关系，便于更加直观的比较各类别特征统计量对链路预测的影响。

1 数据说明和网络构建

1.1 数据说明

本文采用的科学家合作网主要有5个，分别为：netscience、cond-mat、hep-th、geom和GrQc。这5个数据集都记录了科学家之间的协作关系，它们的区别是数据集的大小不同。

(1) netscience网络：是由研究网络科学的科学家组成的合作网络，节点表示从事网络科学研究的科学家，连边表示两个科学家有合作关系。

(2) cond-mat网络：是基于凝聚态物理学家在1995-1999年间发表的预印样本的科学家合作网络。

(3) hep-th网络：包含了1995年-1999年在电子出版物Arxiv中发表高能物理理论相关论文的所有作者之间的合作关系。

(4) geom网络：是由2002年计算几何数据库中作者之间的科学合作关系构建的网络。

(5) GrQc网络：涵盖了1993-2003年间电子出版物Arxiv中广义相对论与量子宇宙学范畴的论文作者之间的科学协作关系。

5个科学家合作网中的节点数和连边数见表1。

表1 科学家合作网数据说明

根据所给数据，本文首先将网络数据文件读取出来并转换成后缀为.txt的文件，为下一步构建网络做准备。

1.2 构建网络

本文使用了科学家合作数据来构建无权无向社交网络。G=(V,E)定义为社交网络的拓扑结构。网络中的边用e=(u,v)∈E来表示，其中u,v∈V，V为网络中的节点集合，E为网络中的边集合。对于网络中每两个节点u,v∈V来说，链路预测就是判断u与v之间存在链接的可能性。针对本文所使用的科学家合作关系数据，网络中节点代表各个科学家，连边代表科学家之间有合作关系，链路预测也就是判断科学家之间有合作关系的可能性。将处理后的数据集分为两部分：训练集ET和测试集EP，本文使用的训练集和测试集的比例为9∶1。

2 网络结构统计特征

研究中，将目前通用的相似性特征分为三类，分别是基于节点度及中心性、基于节点的共同邻居和基于边的共同邻居相似性特征；同时为了进一步提高预测准确率，提出了两类新特征，分别是基于节点的子图特征和基于边的子图特征。

2.1 节点度及中心性特征

节点特征计算了单个节点在网络中的特性，是通过网络结构和单个节点与邻居节点的关系得到的一类相似性特征。该类相似性特征反映了节点在网络中的重要性和节点间的相互关系。包括节点的度、平均邻度、聚类系数、度中心性、特征向量中心性、PageRank中心性，以及介数中心性这7个特征特征。

(1)节点的度。令v∈V，定义v的邻居朋友集合为Γ(v)，即Γ(v)中的节点都为v的邻节点，则节点v的度定义为：

d(v)=|Γ(v)|。

(1)

(2)平均邻度。在无向网络中，该特征是一个常见且比较简单的统计量，它指的是网络中所有节点度的平均值。节点v的平均邻度是v的所有邻居节点度的平均，定义为：

(2)

式中：Γ(v)为节点v的邻居集合；ku代表v的邻居节点u的度。

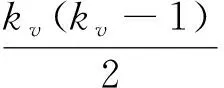
(3)

(4)度中心性。该特征指的是节点在与其直接相连的邻居节点当中的中心程度，中心性较高的节点具有较多的连接关系，因此节点的度值中心性大小体现了节点的活跃特性。假设一个网络中包含N个节点，节点的最大可能度值为N-1，则度为kv的节点归一化的度的中心性值定义为：

(4)

(5)特征向量中心性。是一个节点会由于连接到一些本身很重要的节点，而使自身的重要性得到提升。它指派给网络中的每个节点一个相对得分，对于某个节点分值的贡献，连到高分值的节点比连到低分值节点的贡献大。对于节点v，记FEC(v)为节点v的主要性度量值，则有

(5)

式中：auv为网络的邻接矩阵；β为一比例常数且小于邻接矩阵最大特征值的倒数。

x=cAx。

(6)

式中：x是矩阵A与特征值c-1对应的特征向量，故称为特征向量中心性。

(6)PageRank中心性。PageRank中心性基于网络节点的入度连接计算网络中节点的中心性排序，最初用来对万维网中页面的搜索相关性进行排序。其迭代公式定义为：

(7)

式中：标度常数s∈(0,1)，在本文中取s=0.85。

(7)介数中心性。以经过某个节点的最短路径的数目来刻画节点重要性的特征就称为介数中心性。该特征反映了信息流经给定节点的可能性，节点的介数中心性会随着经过该节点的信息流的增大而增大。具体的节点v的介数定义为：

(8)

2.2 共同邻居特征

共同邻居特征是指两个未连接的节点如果有更多的共同邻居，则它们更倾向于连边。共同邻居特征在预测中具有复杂度低且准确率较高的优势。研究中将共同邻居特征以及由共同邻居衍生出的一些特征归为一个大类，从节点和边的角度出发将共同邻居特征分为基于节点和连边两类特征。

2.2.1 基于节点的共同邻居特征

包括共同邻居CN特征，以及在此基础上得到的Salton特征(余弦相似性)、Jaccard特征、Sorenson特征、HPI特征(Hub Promoted Index，大度节点有利特征)、HDI特征(Hub Depresed Index，大度节点不利特征)和LHN-I特征引入到链路预测中。这7种特征具体表达方式如下：

Covertex(u,v)=|Γ(u)∩Γ(v)|；

(9)

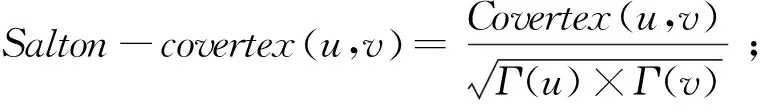
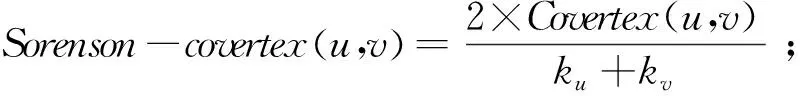
(13)

(14)

Γ(u)是节点u的邻居集合，Γ(v)是节点v的邻居集合，ku和kv分别是节点u和v的度。

2.2.2 基于连边的共同邻居特征

基于连边的共同邻居特征是指节点u和节点v的共同邻居的链接数目。该类特征描述了两个节点及其邻居节点之间的关系，且在预测中具有复杂度低且准确率较高的优势。主要包括共同邻居朋友数特征，以及基于连边的Salton特征、Jaccard特征、Sorenson特征、HPI特征、HDI特征和LHN-I特征。

共同邻居朋友数特征的具体定义式为：

Coedge(u,v)=|friends-measure(u,v)|，(16)

其中，定义δ(x,y)函数为：

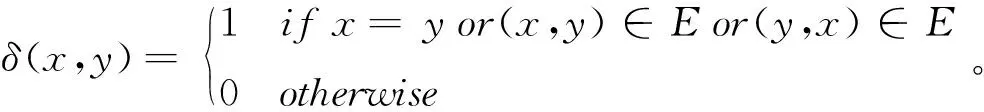
(18)

该特征计算了两个节点u、v的邻居节点之间的连边数，共同邻居朋友数特征将共同邻居节点也定义为有连边的情况，因此共同邻居朋友数特征包含共同邻居特征如图1。

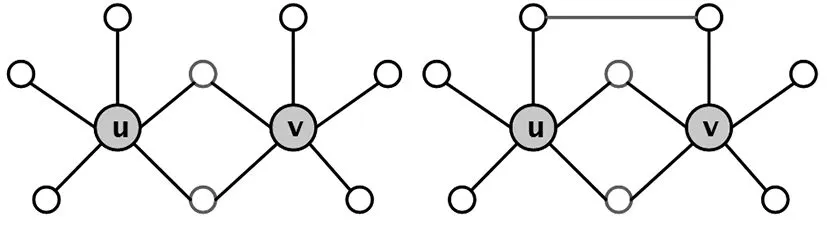
图1 共同邻居与共同邻居朋友数特征

使用朋友数特征，对上面的6个基于共同邻居的相似性特征进行扩展，得到基于共同邻居连边的特征，具体定义为：

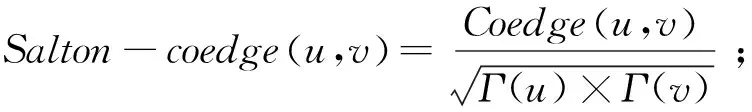
(19)

(20)

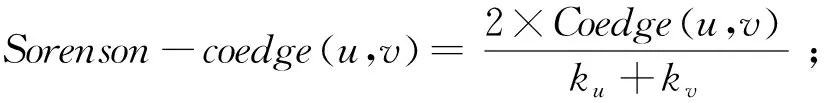
(21)

(22)

(23)

(24)

2.3 子图特征

在节点较多、结构复杂的网络中，子图可以清晰的刻画出网络中的局部结构，有助于分析节点在局部结构中的特性，因此将子图特征引入到链路预测中。本文将子图特征分为基于邻居子图和边子图两大类。

2.3.1 基于邻居子图的特征

首先根据邻居朋友的定义，推导出单个节点v的邻居子图定义如下：

nh-subgraph(v)={(x,y),(y,z),(z,x)∈E|x,y,z∈Γ(v)}。邻居子图就是节点的邻居节点构成的三角形如图2。图中虚线框住的部分就是邻居子图结构。

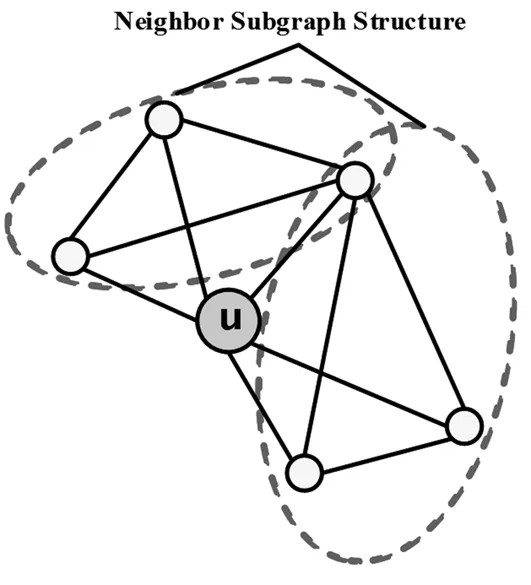
图2 邻居子图结构

在此基础上得出v的邻居子图数目的定义为：

Subgraph-num(v)=|nh-subgraph(v)|。

(25)

根据v的邻居子图和邻居子图数目的定义，可以推导出两个节点u和v的邻居子图和数目定义为：

Subvertex-num(u,v)=max{Subgraph-num(u),Subgraph-num(v)}。

(26)

根据节点u和v邻居子图数目的定义，将基于共同邻居的特征扩展为基于邻居子图的特征，定义如下：

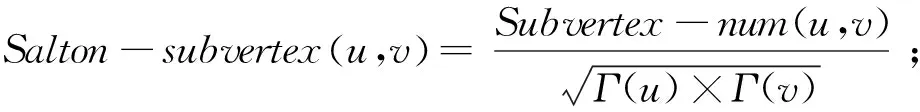
(27)

(28)

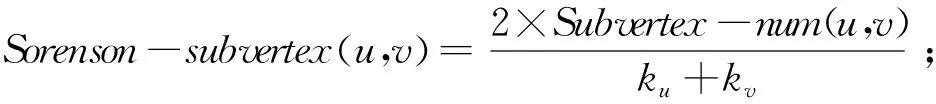
(29)

(30)

(31)

(32)

2.3.2 基于边子图的特征

首先使用邻居朋友的定义，得出节点u和v的边子图特征为：

nh-edge-subgraph(u,v)={(x,y)∈E|x,y∈Γ(u)∪Γ(v)} 。

(33)

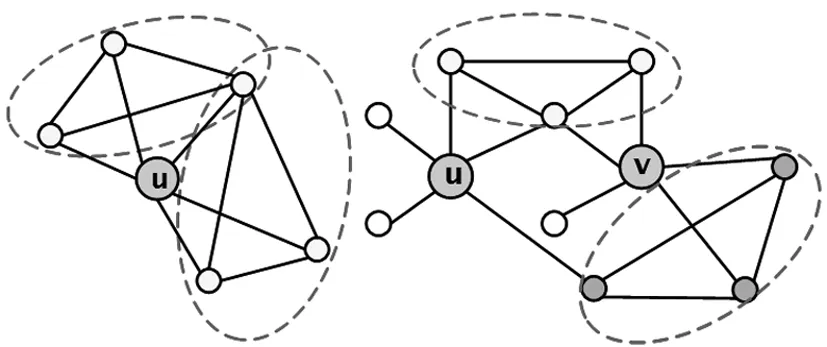
边子图刻画了节点u和v的邻居节点之间构成的三节点图结构如图3，图中虚线框中的部分就是边子图结构。

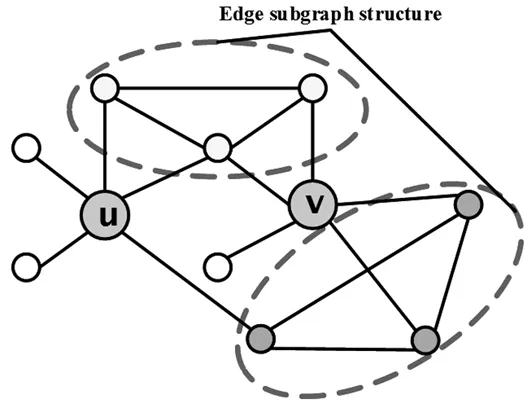
图3 边子图结构

通过上面的定义，能够得出边子图的数目如下：

K-Subedge-num(u,v)=|nh-edge-subgraph(u,v)|。

(34)

将共同邻居连边特征中的朋友特征与边子图特征结合可以得到基于边子图的共同邻居连边特征，定义如下：

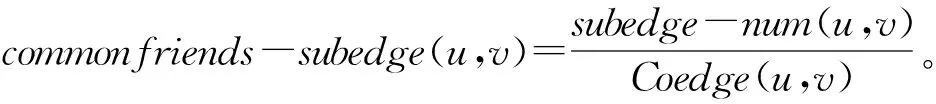
(35)

根据边子图数目的定义，将基于共同邻居的特征扩展为基于边子图的特征，定义为：

(36)

(37)

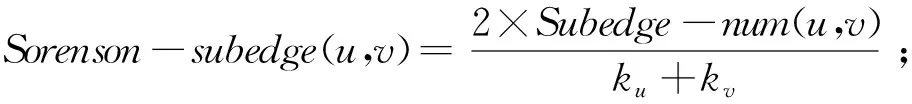
(38)

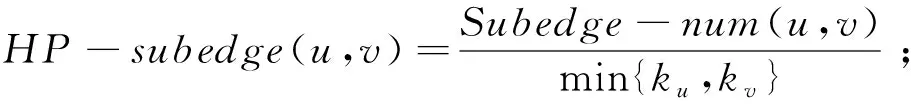
(39)

(40)

3 多类别特征的链路预测方法

研究中首先将提取出的一系列网络结构特征分为五类，然后选取合适的特征选择方法，揭示类内特征之间的关系和影响力，并使用二分类机器学习算法进行链路预测，最后通过评价特征AUC来衡量链路预测的结果。

3.1 多类别特征的构建

特征工程是链路预测当中一个重要环节，在实验中将所有特征分为五类，分别是节点的度和中心性特征、共同邻居节点特征、共同邻居连边特征、基于共同邻居的子图特征以及基于边的子图特征，并计算了在科学家合作网络中节点的特征值。节点属性特征见表2。

表2 节点特征及表示符号

连边特征见表3。分为两类，基于共同邻居节点的特征和基于共同邻居连边的特征。

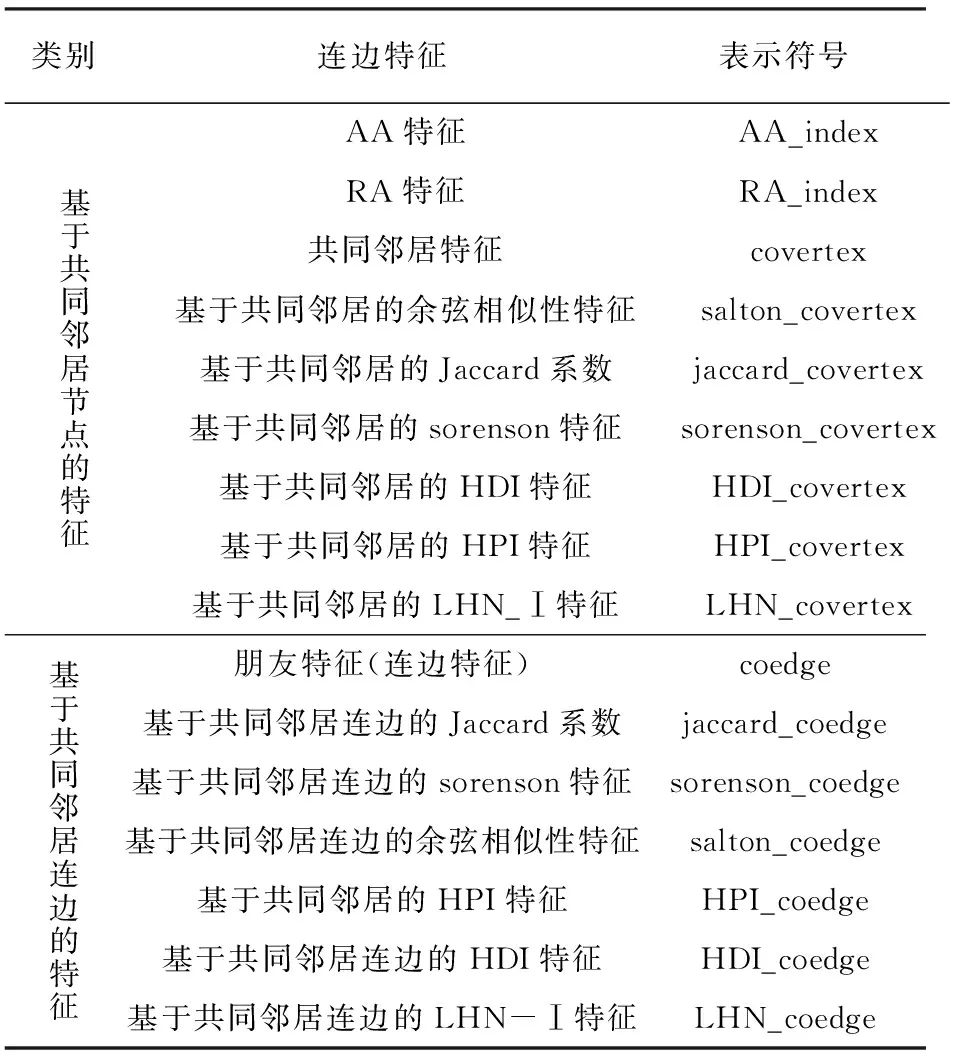
表3 连边特征及表示符号

子图特征见表4，包括基于邻居子图和边子图的两类特征，邻居子图和边子图的定义已在2.3节中做了详细说明。

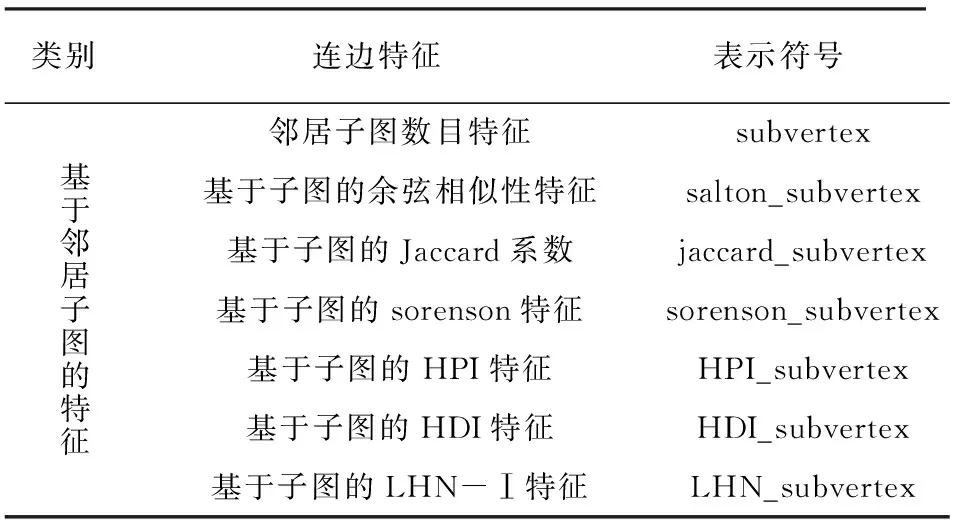
表4 子图特征及表示符号

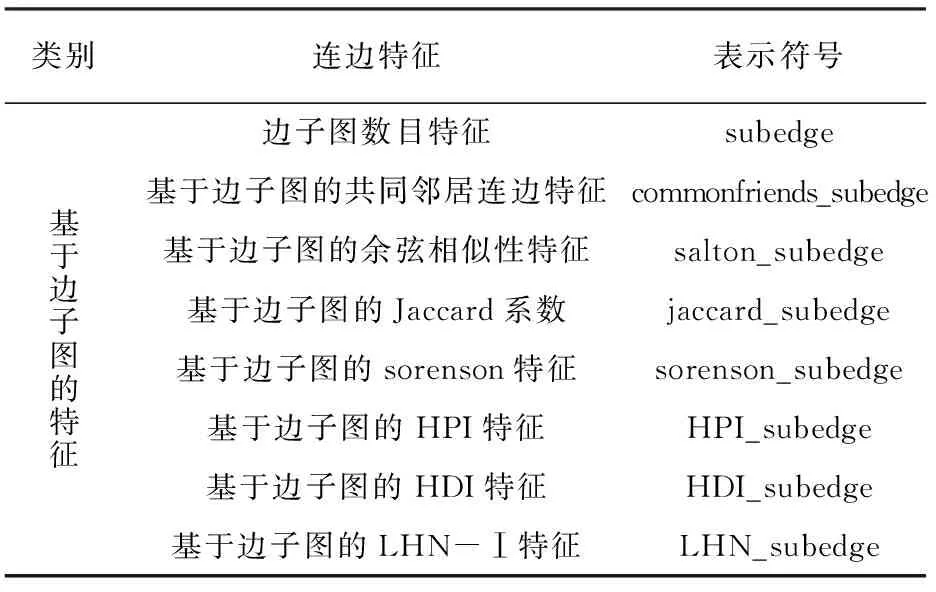
续表4 子图特征及表示符号

3.2 多类别特征的选择

特征选择方法大致可分为封装法、过滤法和嵌入法，这三种方法的主要区别在于特征选择与机器学习分类算法的结合方式不同[27-29]。过滤法是将所有的特征作为初始的特征子集，然后釆用与类别相关的评价特征来衡量特征对类别的区分能力，由于特征选择过程独立于分类过程，过滤方法仅依靠数据的内在属性来评估特征的相关性[30]。封装法是将模型假设搜索加入到特征选择过程中，即搜索算法被“封装”到分类模型中，是以达到最大分类准确率为引导的一类特征选择方法。在封装模型中，分类算法被当作一个黑盒用来评价特征子集的性能，其特征选择是利用分类学习算法的性能来评价特征本身的优劣[31]。嵌入法是过滤法和封装法的综合，将特征选择方法嵌入到模型学习中。嵌入法的分类效果取决于选择的特征模型和具体学习算法。其中，最关键的就是损失函数和参数的确定。这也是该方法中的难点，需要靠一定的经验来寻找到最优参数，使得特征选择结果最佳[32-33]。基于嵌入法存在上述缺点，因此在后续实验中不考虑该特征选择方法。

综合过滤法与封装法各自的优劣和研究中普遍使用的方法的优缺点，本文采用了最大信息数与基于XGBoost模型的特征排序相结合的特征选择方法。

基于XGBoost模型的特征排序方法本质上是根据XGBoost算法的预测性能来衡量特征的优劣，在模型训练过程中，可以得到每个特征的评分值。分值越高说明特征在模型分裂决策树过程中的权值越大，即特征对模型预测效果有着巨大的影响，特征分数值越高，则该特征在预测过程中越重要。

最大信息数(maximal information coefficient, MIC)是2011年发表在science上的一种基于互信息的新奇关联方法[34]，具备普适性、公平性和对称性的特点。普适性是指MIC支持多种类变量间的函数关系及非函数关系；公平性是指在样本量足够大的情况下，能对不同类型单噪声程度相似的相关关系赋予相近的相关系数；对称性是指MIC(X,Y)=MIC(Y,X)[35-36]。MIC的计算主要包括三个步骤：首先对于给定列数i和行数j，将变量(X,Y)构成的散点图进行i列j行网格化，并求出最大互信息值；然后对最大的互信息值进行归一化；最后将不同尺度下互信息的最大值作为MIC值。MIC的定义如下：

(41)

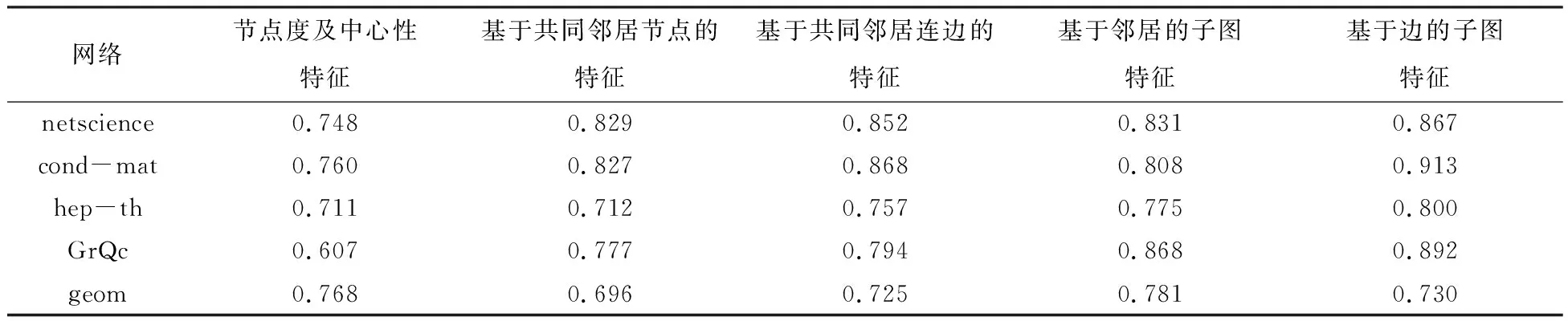
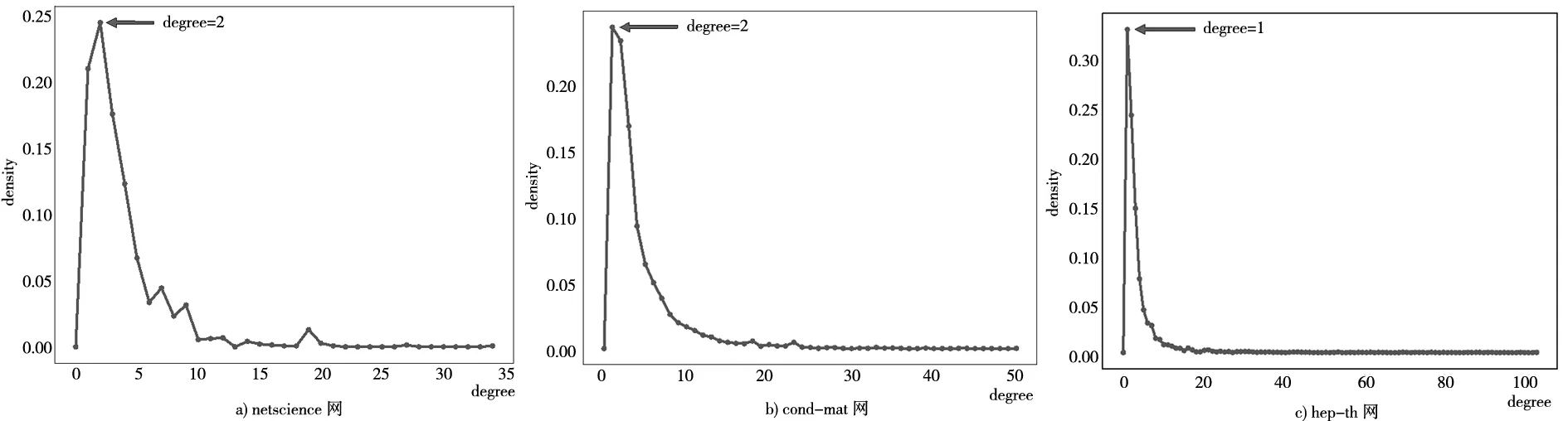
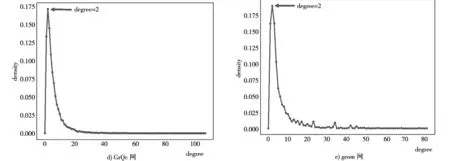
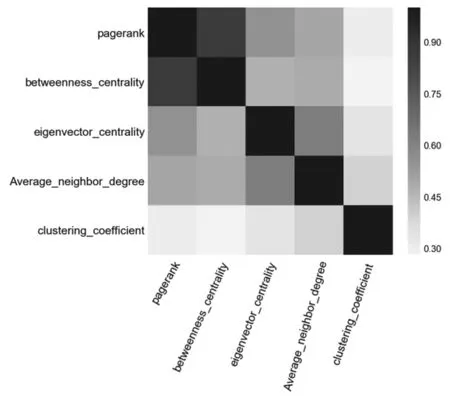
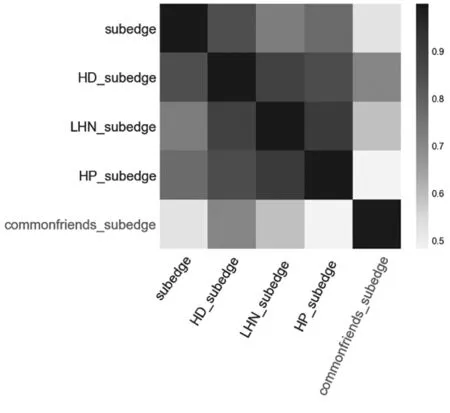
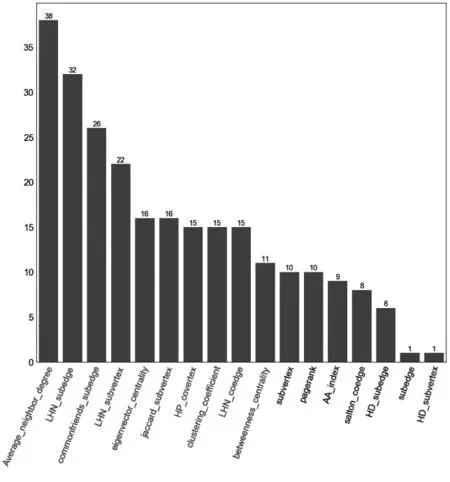
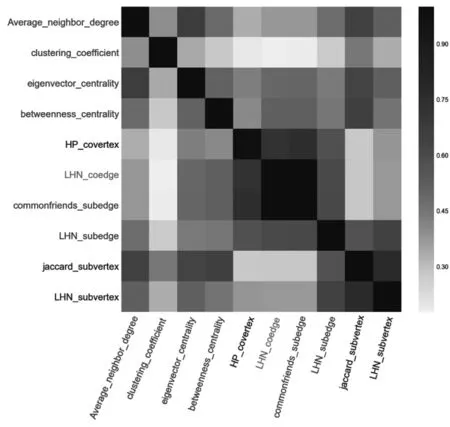
式中：I[X;Y]表示变量X和Y之间的互信息；|X|,|Y|表示散点图网格在X和Y方向上分别被分成了多少段，|X||Y|

本文利用MIC来分析相似性特征类内和类间的相互关系，定义MIC(fi,fj)为任意两个相似性特征fi和fj之间的相关性(也是冗余性)。MIC(fi,fj)的值越大，说明fi和fj之间的相关性越高，即相似程度越高，互为冗余特征。MIC(fi,fj)=0说明fi和fj之间相互独立。

3.3 XGBoost算法

XGBoost算法的全称为Extreme Gradient Boosting，是一种基于决策树的分布式高效梯度提升算法[37]。通过集成多个性能较差的弱学习器而形成一个强学习器，从而很好的拟合训练数据并描述输入输出数据间的复杂非线性关系，提升计算精度，确保模型的计算效率。XGBoost算法在传统GBDT算法的基础上进行了改进，相比于只利用一阶导数信息的传统GDBT，XGBoost对损失函数进行了二阶泰勒展开，且在目标函数中增加了正则化项，整体求最优解，从而控制目标函数和模型的复杂程度，有利于防止过拟合，提高模型的泛化能力[38]。XGBoost算法步骤主要包括定义树提升模型、目标函数构建、梯度提升策略和目标函数优化。

3.4 评价特征

本文使用AUC(area under the receiver operating characteristic curve)作为评价特征，它是最常用的一种衡量特征，从整体上来衡量算法的精确度。AUC是计算在测试集中随机选择一条边的分数值比随机选择的一条不存在的边的分数值高的概率。具体过程为每次随机从测试集中选取一条边，再从不存在的边中随机选择一条，如果测试集中的边分数值大于不存在的边的分数，就加1分；如果两个分数值相等，就加0.5分。这样独立比较次，如果有次测试集中的边分数值大于不存在的边分数，有次两次分数值相等[39]，则AUC定义为：

(41)

4 实验结果分析

4.1 基于科学家合作网的链路预测结果分析

基于科学家合作网，使用上述五类网络结构特征进行链路预测，并分析实验结果。在对5类相似性特征分别使用XGBoost算法进行链路预测，并与传统预测方法比较的基础之上，接下来又针对5个科学家合作网，使用机器学习算法XGBoost对5类特征类别间的预测结果进行了比较分析见表5。

表5 5种科学家合作网的链路预测结果

根据表中的预测结果分析可知，在前4种科学家合作网中，使用基于边子图的特征得到的AUC值最高，因此该类特征在链路预测中的效果最好。由于科学家合作网作者之间的合作关系呈现的主要特征就是边子图形式，因此基于边子图特征的预测准确率高。

在geom网络中，邻居子图特征的预测结果要高于边子图特征，为了探究其具体原因，从网络结构出发，对5个科学家合作网的度分布和社团特性进行了具体分析。

根据图4的网络度分布，发现科学家合作网的度分布呈现相同的趋势，度值较小的节点在网络中的比例较大。度值范围在0～5之间的节点在网络中的比例在70%～80%左右，且网络中占比最大的节点度值集中在1～2。由此可知，科学家合作网中的社团结构较为明显。

图4 5个科学家合作网度分布

根据表6可以看出与其他4个网络相比，网络geom的模块度较低且社团数量远远高于其他网络。因此该网络的聚合程度较低，即节点之间的联系不够紧密。这样就会导致社团划分之后的社团数量很多。

根据图5分析可知，构成邻居子图至少需要4个节点，边子图由于计算的是两个节点之间的结构，因此构成该结构至少需要5个节点。而在geom网络中社团数目较多，因此包含5个节点以上的社团结构的比例较少，构成边子图的可能性也较低，因此在预测中，邻居子图特征的预测结果高于边子图特征。

表6 网络模块度及社团数量

图5 邻居子图和边子图结构对比图

4.2 基于节点的类内特征分析

为了具体分析每类特征对链路预测的影响，本文在接下来的实验中以netscience网络为例，进一步对每类特征做了特征排序以及特征相关性分析。

如图6基于分类模型算法得到的节点特征影响力排序。从中可以看出，该类特征对链路预测的影响力依次递减。PageRank中心性对链路预测的影响最大，节点的度和度中心性对链路预测的影响最小。

图6 节点特征排序

4.2.1 特征相关性分析

使用最大信息数(MIC)计算得到的特征之间的相关性如图7。这5个特征与其它特征之间的相关性均低于0.9，即这些特征都是相互独立的，它们在链路预测中的作用不同，因此这些特征之间不可以相互替代。

图7 特征相关性

4.2.2 链路预测结果

将节点属性特征作为模型的输入，使用分类器模型预测网络中的链路得到链路预测AUC值见表7。从表中可以看出，使用所有节点特征得到的AUC值为0.748，去掉特征排序中影响力等级最低的节点的度和度中心性后，AUC值为0.711，与所有特征的AUC值相差较小，所以节点的度和度中心性特征对链路预测结果影响非常小，因为通过计算发现节点的度值在1～30之间变化，差距较小，因此该特征不足以区分节点间差异。度中心性计算的是一个节点的度值占整个网络最大可能度值的比例，而使用的科学家合作网网络节点数为7 886，网络最大可能度值也就是7 886，导致计算度中心性时分母与分子差距较大，得到的每个节点的度中心性值相差很小，无法体现出不同节点之间的差异。在去掉节点的度和度中心性的基础上，又根据特征相关性，发现剩余的5个特征之间的相关性都较小，因此这些特征都是相对独立的。通过以上去冗余、去相关，可以得到该类特征的最优特征子集U1，U1={Average_neighbor_degree, eigenvector_centrality, pageran-k，clustering_coefficient，betweenness_centrality}

表7 链路预测结果

4.3 子图特征分析

使用基于XGBoost模型的特征排序可以得到基于邻居子图的特征的影响力分值。将得到的影响力分值进行整理、排序，绘制。基于邻居子图相似性特征的影响力排序柱状图如图8。从图中可以看出，部分特征影响力分值较高，如jaccard_subvertex、HD_subvertex、LHN_subvertex和subvertex，这些特征对链路预测影响较大；其他基于邻居子图特征影响力分值较低，如HP_subvertex的分值最低，因此这个特征对链路预测影响较小。

图8 子图特征排序

4.3.1 特征相关性分析

特征排序前4的子图特征之间的相关性如图9。这4个特征中jaccard_subvertex和HD_subvertex之间的相关性较高，说明这2个特征比较相似。LHN_subvertex和subvertex特征与其他特征之间相关性较低，说明这两个特征在预测中相对独立。

图9 基于子图特征相关性

4.3.2 链路预测结果

使用基于邻居子图相似性特征作为XGBoost模型的输入得到的AUC值与进行特征选择后的AUC值见表8。从表中可以看出，使用所有特征得到的AUC值为0.831，只保留特征排序中影响力等级前4的特征后，AUC值为0.825，与所有相似性特征的AUC值相差较小，所以这些特征对链路预测结果影响较小。在去掉影响力低的特征基础上，又根据特征相关性，去掉了强相关特征中的HD_subvertex，得到的AUC值为0.705，与上一步的AUC值差距较大，分析原因发现，虽然jaccard_subvertex和HD_subvertex之间的相关性较高，可能是冗余特征，但是这两个特征在影响力排序中占据第1和第2位，十分重要，删除其中一个会对预测结果影响较大。因此在去冗余、去相关的时要综合考虑特征排序和相关性，根据特征选择去除冗余特征之后，可以得到基于邻居子图相似性特征的最优子集U2，U2={jaccard_subvertex，HD_subvertex，LHN_subvertex，subvertex}

表8 链路预测结果

4.4 基于边子图的特征

使用基于XGBoost模型的特征排序方法，可以根据特征特征在模型训练过程中的重要程度得出特征特征的影响力分值。通过基于XGBoost模型的特征排序方法，可以得到基于边子图特征的影响力分值。该影响力分值得到的影响力排序柱状图如图10。从图中可以看出，部分特征影响力分值较高，如commonfriends_subedge、subedge、LHN_subedge、HD_subedge和HP_subedge，这些特征对链路预测影响较大；其他邻居子图相似性特征影响力分值较低，如sorenson_subedge的分值最低，因此这个特征对链路预测影响较小。

图10 子图特征排序

4.4.1 特征相关性分析

通过最大信息数(MIC)可以衡量各个特征间的相关性。MIC值的范围是0～1，MIC值越大，说明两个特征间相关性越高，越相似。去掉影响力排序后3位的salton_subedge、sorenson_subedge和jaccard_subedge后，得到的前5位边子图相似性特征之间的相关性如图11。这5个特征可以分为三类，第一类为commonfriends_subedge，这个特征仅与其本身的相关性较高，与其他特征之间的相关性很低，因此相对独立；第二类为subedge和HD_subedge，这两个特征与除了第一类的其他特征之间的相关性较高，分值集中在0.7～0.9；第三类为LHN_subedge和HP_subedge特征，它们之间具有很强的相关性。

图11 基于子图特征相关性

4.4.2 链路预测结果

使用基于边子图特征作为模型的输入得到的AUC值见表9。从表中可以看出，使用所有特征得到的AUC值为0.867，只保留特征排序中影响力等级前5的特征后，AUC值为0.854，与所有特征的AUC值相差很小，所以这些特征对链路预测结果影响较大。在去掉影响力低的特征基础上，又根据特征相关性，去掉了第二类强相关特征中的HP_subedge，得到的AUC值为0.850，与上一步的AUC值相同，因此根据相关性去掉部分冗余特征后，可以达到与之前接近的预测效果。根据特征选择去除冗余特征之后，可以得到子图特征的最优子集U3，U3={commonfriends_subedge，subedge，HD_subedge, LHN_subedge }

表9 链路预测结果

4.5 所有特征分析

为了分析相似性特征在链路预测中的重要性，删除冗余特征，我们将单类特征选择分析中得到的最优子集U1、U2、U3、U4、U5合并为特征子集U，并对该特征子集中的相似性特征使用基于XGBoost模型的特征排序方法进行了重要性排序，结果如图12。根据特征排序可知，这些特征在预测中的重要性呈现递减趋势。因此，在链路预测中，排序靠前的特征特征比排序落后的特征更具影响力。在后续分析中保留了前10个影响力大的特征。

图12 netscience网络所有特征排序

为了分析特征之间的相互关系，删除在链路预测中相关性非常高的相似特征，我们对前10个影响力大的相似性特征使用MIC进行相关性分析如图13。5类特征中， LHN_coedge和commonfriends_subedge特征之间有较强相关性；对于这些强相关特征，在链路预测中只保留其中一个即可，因此，结合图123特征排序，删除了排序较后的LHN_coedge特征，使得最终保留的9个特征之间都相互独立。

图13 netscience网络排序前15的特征相关性

将所有特征作为XGBoost模型的输入，使用分类器模型预测网络中的链路得到链路预测AUC值见表10。从表中可以看出，使用未进行特征选择的所有特征得到的AUC值为0.967，而使用单类特征选择之后得到的子集U的AUC值为0.965，与特征选择之间相差很小，说明特征选择过程可以帮助我们删除预测中部分冗余特征。对特征子集U进一步做特征选择，去掉特征排序中影响力等级低的相似性特征以及特征相关性中的部分强相关特征后，AUC值为0.959，与特征子集U的AUC值相差较小，说明在去冗余和去相关之后得到了与原始特征非常接近的预测结果。说明特征选择在多类别的网络结构特征中起到了关键性作用，进行特征选择可以在降低特征维数的同时，保证预测效果达到与特征选择之前相近的水平。

表10 链路预测结果

5 结 论

本文提出基于多类别网络结构特征的链路预测方法，对科学家合作网络中的作者合作关系进行了研究。首先根据短信数据构建了无向无权社交网络。其次，提取了一系列网络结构特征并将其征分为五类，包括节点特征、基于共同邻居的节点特征、基于共同邻居的边特征、基于邻居的子图特征和基于边的子图特征。同时使用基于模型的特征排序和最大信息数特征选择方法分析了特征之间的关系，去除了冗余特征。最后，通过机器学习算法模型进行链路预测。使用这种链路预测框架对网络进行分析，可以提高链路预测的准确性。与此同时，能够揭示各个特征在模型训练中的重要性和特征之间的相互关系，通过类内和类间特征相关性分析，更直观的找到网络中的强相关特征，即可替代性强的冗余特征。在链路预测中，选取合适的特征选择方法去相关、去冗余的过程可以应用到其他社会网络中。