认知无线电中基于压缩感知的非重构频谱检测算法
2020-02-24邵建华
安 爽, 邵建华
(南京师范大学物理科学与技术学院, 南京 210023)
无线通信现在所面临的困境之一就是频谱资源的严重不足,根据美国联邦通信委员会(Federal Communications Commission,FCC)表明,频谱的使用是处在一个动态的变化范围内,因此很多的频段空间的利用率是很低的。
FCC于2003年给出了认知无线电(cognitive radio,CR)的定义,它允许没有频谱使用的次要用户(secondary user,SU)去感知并使用主要用户(primary user,PU)的空闲频谱[1]。CR是解决当前阶段下的频谱紧缺的有效方式,而频谱感知技术正是CR实现应用的重要一环[2]。频谱感知环节、信道分析环节、频谱分配等技术使得CR可以感知到处于空闲的频谱资源并加以合理的分配使用[3]。压缩感知(compressed sensing,CS)[4]技术可以实现在大大低于Nyquist取样率的情况下来得到取样值,从而减少了宽带频谱检测的难度。2007年,Tian等[5]首先将CS技术用到了宽带频谱感知之中,随之又提出了在CS理论下基于循环检测的一种算法[6]。文献[7]提出在CS理论下稀疏度估计的自适应算法,对信号稀疏度的变化进行跟踪,继而获得压缩采样数据实现检测。文献[8]提出一种在CS理论下基于L1范数约束的最小二乘迭代的一种算法。但上述这些方法均须相关的恢复算法,这就使得计算过程变得相对烦琐,另外恢复的精确性也会对检测的性能造成一定影响。
现提出一种对信道内的信号进行压缩得到信道组采样协方差矩阵并利用其对角线数据与能量检测结合的单节点及多节点频谱检测的方法。首先将信道进行划分,次要用户去接收每个信道的压缩测量数据获得采样协方差矩阵,对该矩阵的对角线数据再进行下一步的统计处理,根据预先设定的门限值进行对照判断,这个过程不需要任何重构,不但降低计算的复杂度,且很大程度上缩短检测时间。
1 系统模型及检测算法
1.1 单用户检测模型及算法
单用户检测模型如图1所示。设整个频段的带宽为B,将频段分成L个小信道,SU轮流去感知这L个信道中的占用情况,检测出未被占用的频段并去使用。

图1 单用户检测模型示意图Fig.1 Schematic diagram of single user detection model
图2表示单个用户频谱检测算法框图。

图2 单用户检测算法框图Fig.2 Single user detection algorithm block diagram
在SU处所接受的信号可以表示为
(1)
式(1)中:hi是第i个信道的信道增益;xi为第i个信道上的信号;wi是一个加性高斯白噪声,它的均值是0,方差是σ2。令si=hixi,当SU接收到来自主用户的信号后,应用CS理论可将接收到的信号表示为
y=Φ(si+wi)
(2)
式(2)中:Φ∈CM×N(M≤N)是高斯随机测量矩阵,该矩阵可以很大程度上满足有限等距性质,同时重构过程中的迭代次数也最少[9]。当每个信道重复上述过程获得压缩测量值后,L个信道内信号的压缩测量值就可以构成矩阵:
Y=[y1,y2,…,yL]T
(3)
Y里面存储着每个信道的压缩测量值。由此可以得到L个信道的采样协方差矩阵为
(4)
由式(3)所得到的矩阵Y的维度为L×M,由Y的表示形式可以看出,矩阵Y每行的数据为每个信道的压缩测量值;而S的大小则为L×L,S的对角线数据是为同一个信道内一定时间内的压缩测量值的平方。这时利用对角线数据进行压缩所获得的信号的能量积累,如果这个值高于一定的门限,则认为有这个信道里面有信号存在,否则只有噪声。能量检测的结果依赖于所接收到信号的信噪比[10,11]。
每个信道中的检测统计量可表示为
(5)
式(5)中:N为采样点数。根据式(5)以及S的对角线数据可以得到每个信道中的压缩能量ξL,再将该值与此前设定的门限作对照以判断信道中是否有信号存在。
对于恒定的虚警概率Pf,在此设定的门限γ为
(6)
如果ξi>γ则判断为信号存在记作D1,感知结果记为1;反之如果ξi<γ,则判断为信号不存在记作D0,信道中只有噪声,感知结果记为0。统计所得的检测概率为
(7)
式(7)中:H1表示在信道中有信号存在;N1是感知的过程中判定信号存在的次数;Ns表示仿真的次数,当有充足的仿真数Ns时,仿真结果与理论结果也就越相近。
1.2 多用户检测模型及算法
由于单节点检测存在隐藏终端或深度衰落等缺陷[12],这就导致检测结果可能会出现偏差,为了避免这类问题所导致的检测不准确等后果,因此又提出多用户协作检测。其系统模型如图3所示。假设一共有P个次要用户,那么就会产生P个采样协方差矩阵,每个SU将自己的判决结果发送给融合中心,再由融合中心给出最终判决。
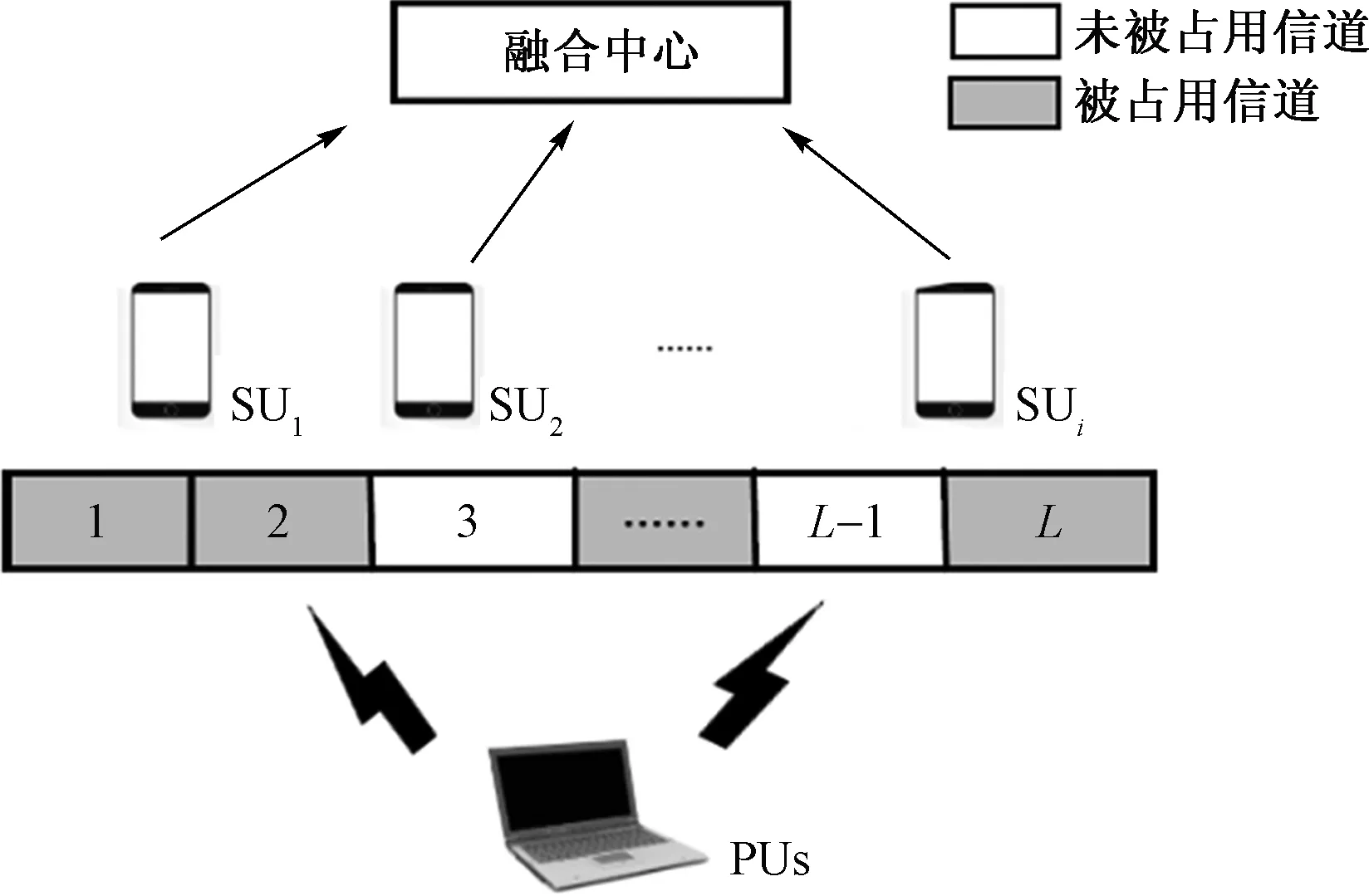
图3 多用户检测模型示意图Fig.3 Schematic diagram of multi-user detection model
图4表示多个用户频谱检测算法框图。
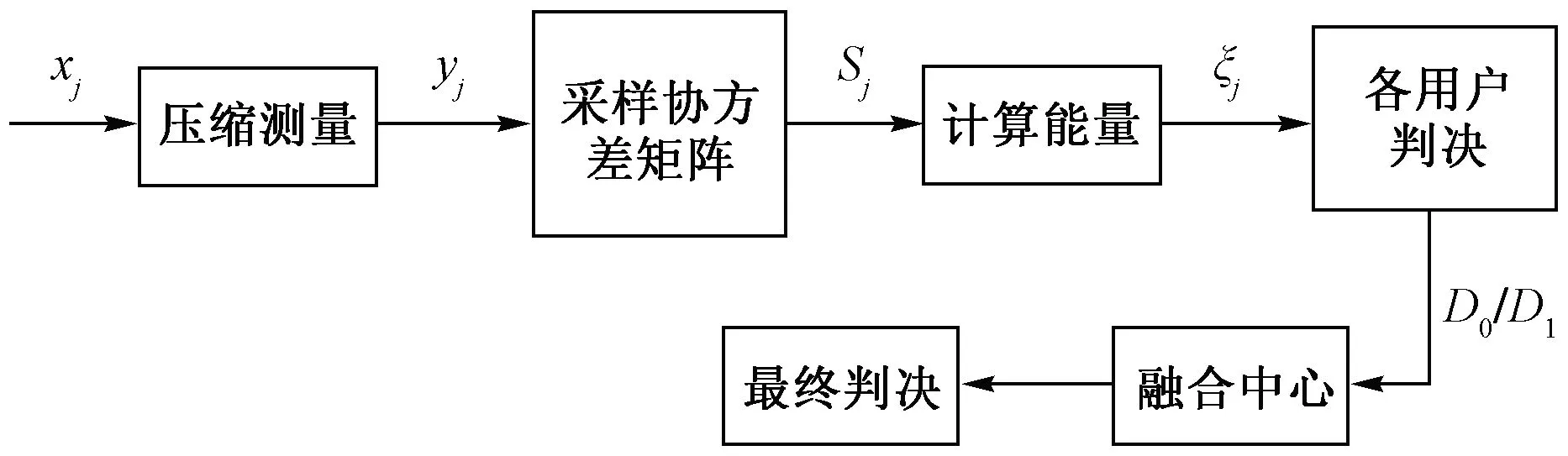
图4 多用户检测算法框图Fig.4 Block diagram of multi-user spectrum detection algorithm
第一阶段处理过程与单个用户的处理大致类似。设一共P个次要用户,则SUj(j=1,2,…,P)接收到来自主用户的信号后,应用CS理论将SUj处收到的来自每个信道的信号表达为
yij=Φ(sij+wij)
(8)
式(8)中:sij=hijxij,hij为第i个信道中第j个用户发送端与接收端之间的增益,xi是第i个信道上的信号;wij是一个加性高斯白噪声,它的均值是0,方差是σ2。
第j个用户在L个信道里的信号压缩测量值可构成矩阵为
Yj=[y1j,y2j,…,yLj]T
(9)
由Yj可得到L个信道的采样协方差矩阵:
(10)
由式(9)所得到的矩阵Yj的维度为L×M,由Yj的表示形式可以看出,矩阵Yj每行的数据为第j个用户获得的每个信道的压缩测量值;Sj的维度是L×L,其对角线数据为第j个用户感知的同一信道在一定时间内的压缩测量值的平方,第j个用户根据压缩能量ξij与预设的检测门限γ可以判断第i个信道上是否有PU的存在。如果ξij>γ,则第j个用户判断信号存在记作D1,感知结果记为1;反之如果ξij<γ,则第j个用户判定信号不存在记作D0,信道中只有噪声,感知结果记为0。一旦感知结束,每个SUj将在本身处的判断结果送交给融合中心,然后由融合中心作出最后判断。
2 仿真结果与分析
2.1 单用户检测仿真分析

图5表示在不同压缩率下信噪比分别为-8、-6 dB情况下重构与否条件下的检测概率。由仿真分析得到,当压缩率提高的时候,检测概率也会提高,当压缩率在0~50%内,信噪比为-6 dB时的结果要优于信噪比为-8 dB时的结果,当压缩率在30%以上时,检测性能较好。且重构情况下的检测概率要明显低于相同信噪比下非重构情况下的检测概率,这是因为重构的精度会影响检测概率。
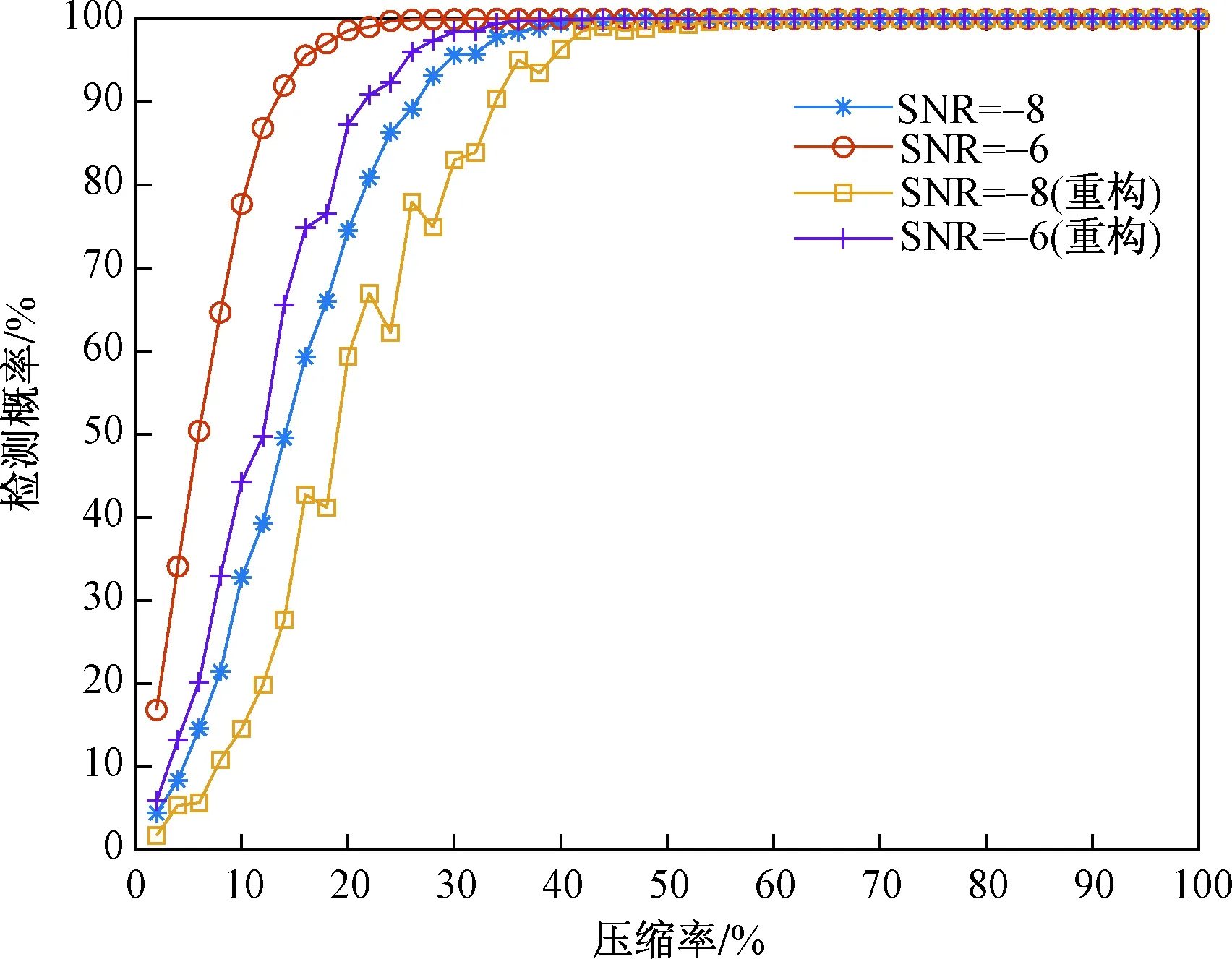
图5 不同压缩率下重构与非重构的检测概率Fig.5 Detection probability of reconstruction and non-reconstruction under different compression ratios

图6 不同压缩率下重构与非重构的检测时间Fig.6 Detection time of reconstruction and non-reconstruction under different compression ratios
图6表示在不同压缩率下重构与否条件下的检测时间对比。根据仿真结果,无论哪种情况,压缩率的提高都伴随着检测时间的增长,并且重构情况下的检测时间要长于非重构情况下的检测时间。
图7表示在不同信噪比且压缩率为30%时重构与否条件下的检测概率对比。根据仿真结果可以得到,无论哪种情况信噪比越大,检测概率也就越高,当信噪比大于-6 dB的时候,可以获得较为理想的检测结果。同样,重构情况下的检测概率要明显低于非重构的情况,其原因仍旧是重构精度会对检测概率造成一定的影响。
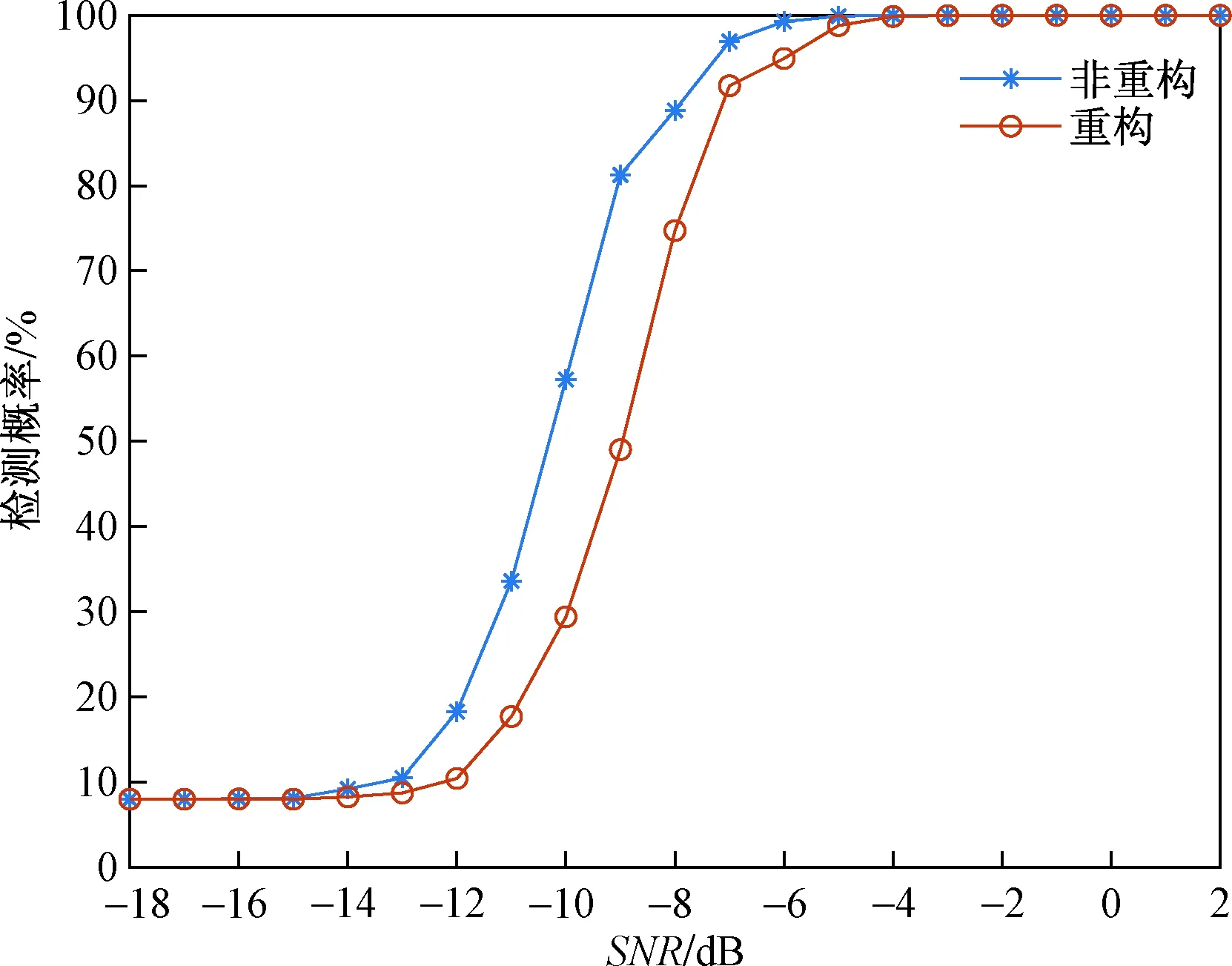
图7 不同信噪比下重构与非重构的检测概率Fig.7 Detection probability of reconstruction and non-reconstruction under different SNR
2.2 多用户检测仿真分析

图8表示不同的压缩率下用户数分别是1、3、5时非重构情况下的检测概率。根据仿真结果可以得到压缩率和用户数的上升也伴随着检测概率的提高。

图8 不同压缩率下不同用户数非重构下的检测概率Fig.8 Detection probability of non-reconstruction of different users under different compression ratios
图9表示在不同信噪比的情况下用户数分别是1、3、5时重构与否的检测概率。根据仿真结果得出,当信噪比增大时检测概率也随之提高,在多个用户下检测的概率总是大于单个用户的概率;并且重构时检测的概率要低于不重构时的概率。
图10表示在不同信噪比情况下,当压缩率为30%,用户数分别是1、3、5时重构与否的检测时间,由仿真得出,用户数增多,检测时间也相应增长,且重构的检测时间比非重构的时间要长。

图10 不同信噪比下不同用户数重构与非重构下的检测时间Fig.10 Detection time of reconstruction and non-reconstruction of different users under different SNR
3 结论
提出了基于CS理论的非重构单用户和多用户合作频谱感知算法。对频段进行信道划分之后应用CS理论获得信道组的采样协方差矩阵,针对压缩率、信噪比以及用户数的差异对其检测概率和检测时间进行仿真。根据仿真结果可得出以下结论。
(1)在非重构情况下,当压缩率在30%以上,信噪比在-6 dB以上时,可以获得较为理想的检测概率,多个用户的检测概率要大于单个用户,但随着压缩率和用户数目的增加,检测时间会增加。
(2)重构情况下的计算复杂度明显要高,不仅检测概率略低,而且检测时间也要长于非重构的情况。
(3)不论是重构还是非重构,最终的检测结果都会因为噪声而受到影响,当信噪比偏低时,所得到的检测结果很差,下一步的研究将侧重于如何优化低信噪比情况下的检测结果。
