渐缩型气动喷砂喷嘴冲蚀模拟分析

2020-02-24王卫强

科学技术与工程 2020年1期

王博, 徐鑫, 王卫强

(辽宁石油化工大学石油天然气工程学院,抚顺 113001)

集输管道表面经常会出现锈斑、污垢等现象,为了解决这一现象,石化行业广泛采用涂层防护工艺,然而管道表面的光亮程度及表面粗糙度严重影响防护工艺的质量[1]。因此,许多表面处理工艺应运而生,如化学试剂清洗、机械抛丸、磨料射流等[2]。同上述几种方法相比,气动喷砂具有抛光度高、粗糙度易控制、内孔清洁度达标等优点；同时,在相同条件下,气动喷砂装置使用成本远低于其他几种方式。在气动喷砂系统中,喷嘴将气动流体的压力内能转化为速度动能,使砂粒在高速气流的携带作用下喷射到构件表面,达到表面清洗的目的。喷嘴结构的稳定性直接影响喷射的效率,但喷砂颗粒流经喷嘴会对自身内壁面造成严重的冲蚀磨损,降低装置的使用效率。目前对喷射器的研究主要集中在气动喷砂装置内流场分析及颗粒轨迹探索,如学者贾光政等[3]运用CFD软件模拟了颗粒在收缩型喷嘴中的运动轨迹,计算了不同粒径流经喷嘴前后的动量变化量；王金东等[4]运用Euler-Lagrange法,对不同运行工况下的气固两相内流场进行了数值模拟,得到了气动流体的运动规律；李晶等[5]利用试验优化方法,对304不锈钢在不同参数下的表面润湿性能进行了分析,并运用聚焦显微镜对结果进行了观察；王金东等[6]通过改变喷嘴的直径对喷嘴内部气固两相流场进行了仿真模拟,得到了压力及速度的分布情况及颗粒撞击壁面的主要位置。针对气动喷射器自身冲蚀磨损的研究鲜有报道。因此,以渐缩型气动喷砂喷嘴为研究对象,运用CFD软件对喷嘴内流场分布及颗粒运动特性进行模拟分析,进而得到喷嘴的冲蚀规律及影响因素。

1 基本假设

(1)设定喷射流体为理想流体,流体遵循绝热流动基本方程。

(2)喷砂颗粒为球形,密度相同,表面光滑。

(3)喷砂颗粒总体积分数小于喷射装置总体积的10%,可作为离散相处理。

(4)忽略喷射颗粒对流体的反向作用力及颗粒与颗粒之间的相互碰撞。

(5)只考虑连续相流体对离散相颗粒的阻力作用,忽略Saffman升力、Basset力及重力等影响。

2 数学模型

2.1 湍流模型

压缩气体为理想气体,喷嘴内流体流动速度较快,流态为湍流,因此,建立流动湍流模型。喷嘴内流场并未出现漩涡流动,流动介质黏度较小。因此,选用Launder和Spalding于1972年提出的标准k-ε湍流模型[7]。标准k-ε模型中,k和ε是两个基本的未知量,与之相对应的输运方程为

k方程：

Gk+Gb-ρε-YM

(1)

ε方程：

(2)

式中：ρ为流体密度,kg·m-3；k为湍动能；ε为湍动能耗散率；μt为湍动黏度；Gk为平均速度产生的湍动动能；Gb为浮力产生的湍动动能；YM为湍流脉动扩张引起的贡献；σk、σε分别为k、ε对应的普朗特数；C1ε、C2ε、C3ε为经验常数。根据文献[8]实验平台测得的实验数据,取值分别为σk=1.0,σε=1.3,C1ε=1.44,C2ε=1.92,C3ε=0.09。

2.2 颗粒运动模型

对于气动喷砂两相流场,固体颗粒体积分数较小,可作为离散相处理,认为颗粒只受Stokes阻力的作用,忽略颗粒间的相互碰撞及剪切应力等所产生的影响[9]。根据牛顿第二定律,单位质量固体颗粒在气动阻力作用下的运动方程为

(3)

(4)

(5)

(6)

式中：FD为阻尼系数；u为气体流速,m·s-1；up为颗粒流速,m·s-1；CD为阻力因子；Re为相对雷诺数；ρp为颗粒密度,kg·m-3；μ为流体动力黏度,Pa·s；dp为固体颗粒的粒径,mm；对于球形颗粒,在一定雷诺数范围内,a1、a2、a3为常数[10]。

2.3 冲蚀模型

采用Fluent中定义的冲蚀模型[11]对气动喷砂喷嘴进行模拟计算。冲蚀速率计算公式为

(7)

式(7)中：mp为颗粒质量,kg；C(dp)为颗粒粒径函数[11],取C(dp)=1.8×10-9；v为颗粒相对速度,m·s-1；b(v)为相对速度函数[12],取b(v)=2.6；Aface为壁面面积,m2；α为冲击角度,rad；f(α)为冲击角函数,采用分段线性函数进行拟合[13]。

f(α)=

(8)

2.4 流固耦合

气相采用标准k-ε湍流模型；固相采用拉格朗日法(Lagrange)进行轨迹跟踪。由基本假设可知,气体为连续相,喷射颗粒为离散相,相间耦合求解过程如图1所示。

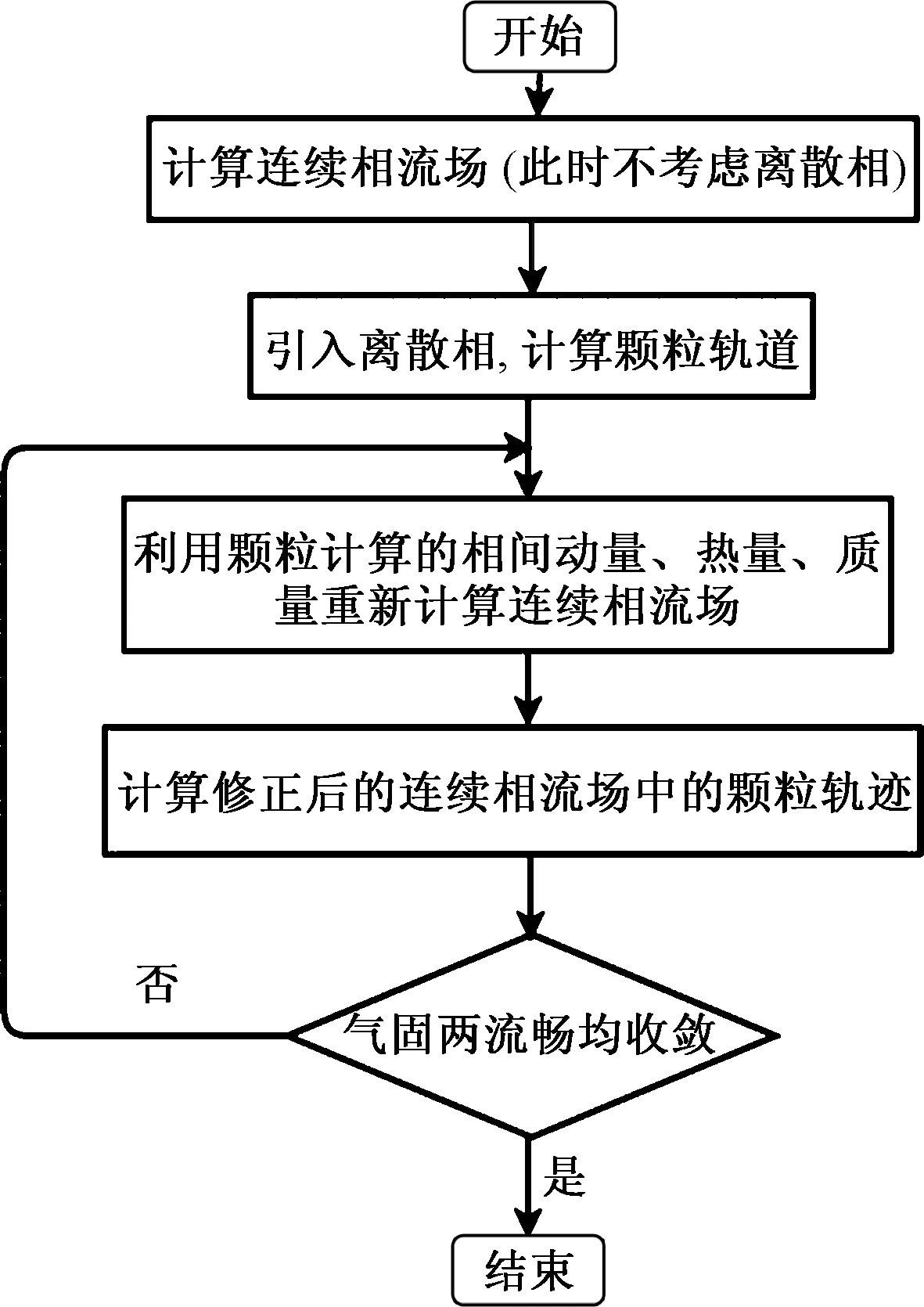
图1 气固耦合流程示意图Fig.1 Flow chart of gas-solid phases coupling

3 计算域及网格划分

3.1 计算域

计算域为喷嘴内流场,考虑到流场的对称特性,取轴对称流场进行分析,计算域模型如图2所示。

图2 计算域Fig.2 Computational domain

设定喷嘴入口为压力入口,壁面为无滑移绝热标准壁面,喷嘴出口为压力出口；入口处离散相颗粒均匀分布,速度沿轴向方向,入口及出口处设定escape条件,壁面设置reflect条件。

3.2 网格划分

运用ANSYS ICEM对渐缩型喷嘴进行结构化网格划分,由于喷嘴近壁面流动较剧烈,因此壁面附近设置4层膨胀层并且局部位置进行加密处理；通过对网格进行无关性检验,最终确定渐缩型喷嘴二维网格总数为15 335,具体网格划分如图3所示。

图3 网格划分Fig.3 Gridding

4 仿真结果及分析

设定喷嘴入口半径为20 mm,出口半径为5 mm；入口总压为6.01×105Pa,出口压力为1.01×105Pa；流体为天然气,密度为0.667 9 kg/m3,颗粒材质为石英砂石,密度为2 650 kg/m3[14]。

4.1 流场分析

选取收缩角为30°的渐缩型喷嘴进行流场分析,压力云图及速度云图如图4与图5所示。

图4 压力云图Fig.4 Pressure cloud map

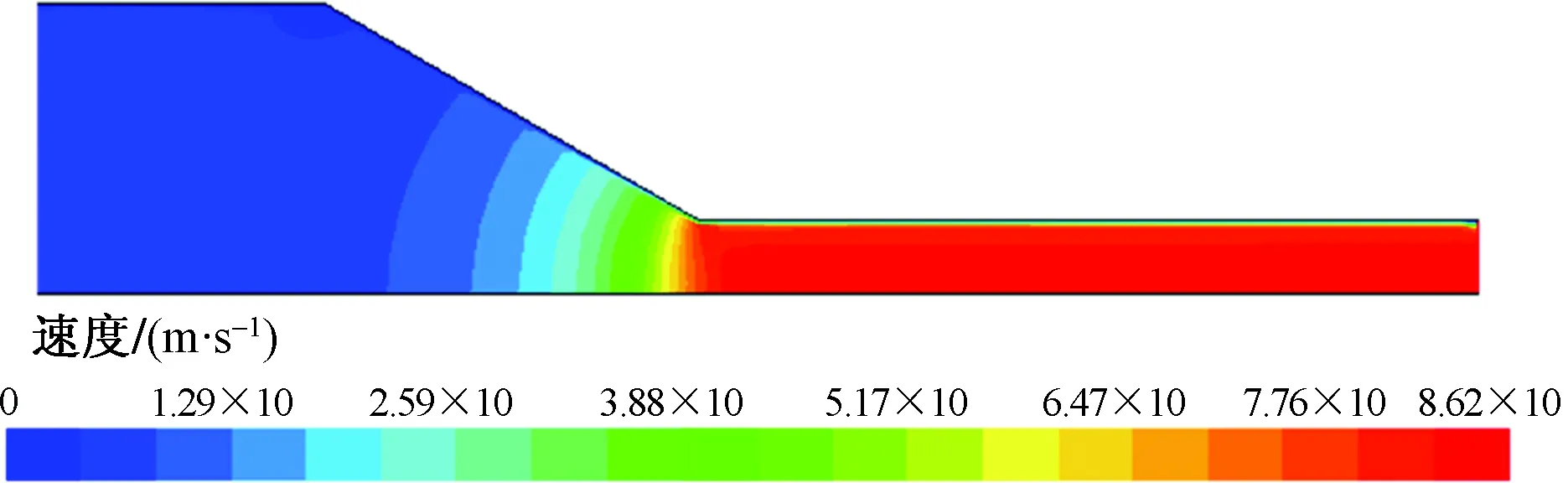
图5 速度云图Fig.5 Speed cloud map

由图4可知,喷嘴入口段压力分布较均匀,收缩段与出口段交界面处压力变化较剧烈,出口段管径缩小导致其内部压力变化梯度较大。

由图5可知,喷嘴入口段及出口段速度分布较均匀,入口处管径较大,因此速度较小,出口段管径缩小,从而使速度急剧增加；收缩段速度变化梯度较大,受渐缩段管径逐渐缩小的影响,速度沿轴向方向呈现层状分布。

为直观地观察喷嘴内部压力及速度的变化规律,绘制喷嘴轴向压力及速度变化曲线如图6与图7所示。

图6 轴线压力变化曲线Fig.6 Axis pressure change curve

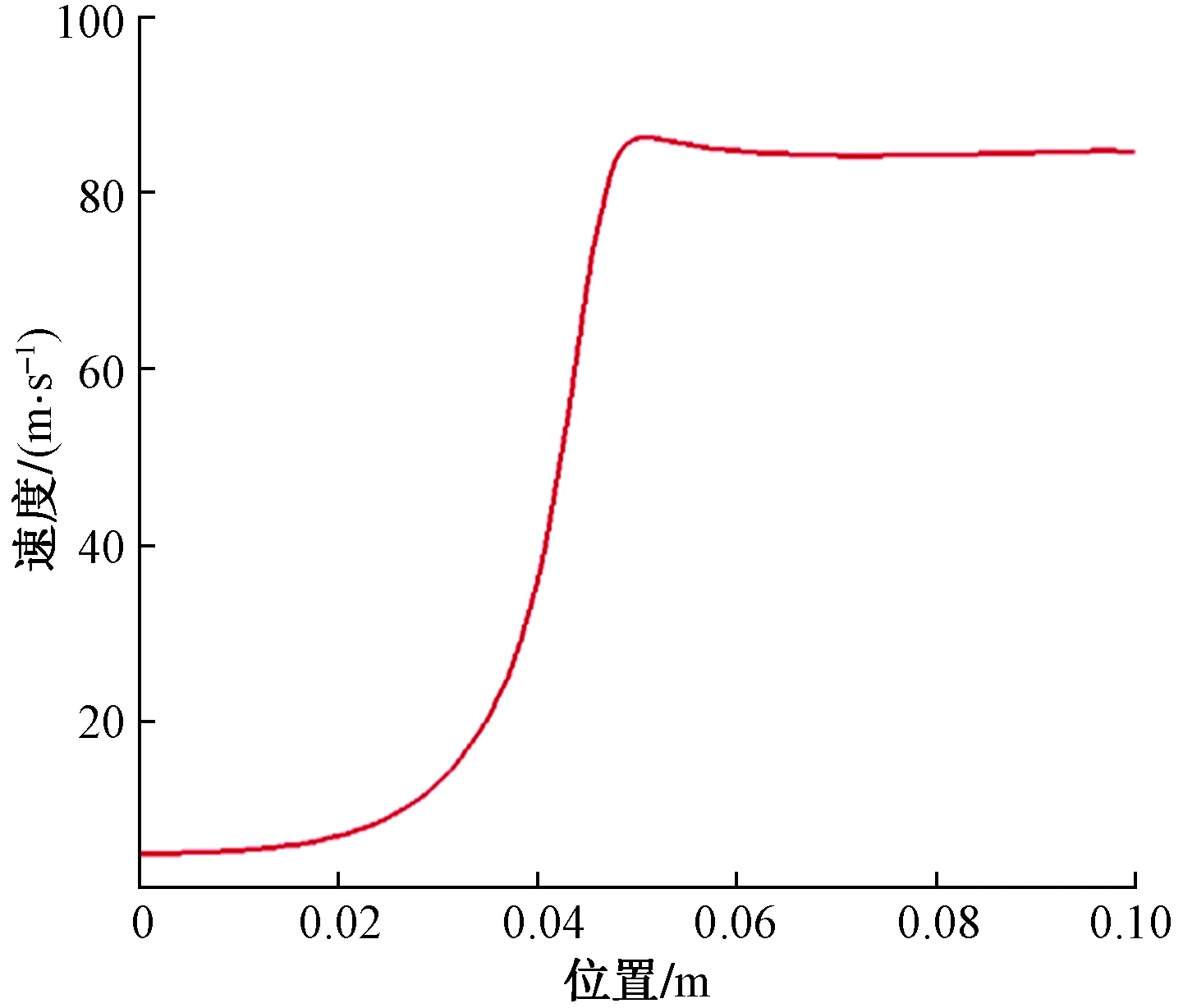
图7 轴向速度变化曲线Fig.7 Axial velocity change curve

由图6可知,喷嘴入口段至收缩段中部位置(0～0.03 m)压力值基本保持不变,近似稳定在1.031×105Pa；由于喷嘴收缩段管径逐渐减小的原因使收缩段中部至收缩段出口附近(0.03～0.05 m)的速度迅速降低,由1.031×105Pa降低至1.005×105Pa；由于喷嘴出口段管径缩小的原因,喷嘴收缩段末端至喷嘴出口(0.05～0.1 m),速度仍呈现降低的趋势,根据收缩段与出口段速度降低的曲线斜率可知,出口段速度降低的速度远小于收缩段。

由图7可知,喷嘴入口段(0～0.02 m)速度变化梯度较小,基本稳定在4 m·s-1；喷嘴收缩段(0.02～0.044 m)速度变化梯度较大,呈迅速增加的趋势,并且在距收缩段出口的0.044 m处取得速度最大值,值为84 m·s-1；喷嘴收缩段与出口段交界处附近至出口处(0.044～0.1 m),速度略微较小后保持恒定。

4.2 冲蚀分析

固体颗粒对气动喷砂喷嘴壁面的冲蚀程度可用冲蚀率进行定义[15]。冲蚀率的本质为单位时间内固体颗粒对壁面金属材料的切削作用。由材料冲蚀的机理可知[16],固体颗粒在流体的带动下以很高的冲击速度撞击到材料表面,从而形成较为严重的冲蚀基坑,小直径颗粒由于质量较小会脱落到流场内,随着流体的湍动作用继续流动,大直径颗粒直径由于质量较大的原因,部分颗粒会滞留在材料表面,削弱后续颗粒对材料的冲蚀作用。颗粒对材料的冲蚀过程如图8所示。

图8 颗粒冲蚀过程示意图Fig.8 Schematic diagram of particle erosion process

设定颗粒粒径为0.2 mm,颗粒质量流率为0.001 kg·s-1,以收缩角度为30°的渐缩型喷嘴为例分析颗粒对壁面的冲蚀现象,冲蚀云图如图9所示。

2018年11月5日消息，天猫方面宣布，天猫超市一小时达已接入饿了么配送，首批已覆盖北京、上海、广州、深圳、杭州、武汉、福州、成都等全国八大城市，陆续还将接入更多城市。据了解，天猫超市一小时达目前已开进北京、上海、成都、杭州、武汉、重庆、广州、深圳等全国21个城市并铺设了近400个前置仓，同时和北京、杭州共45家便利店合作。天猫超市一小时达负责人刘文博表示，“双方的合作将不断满足消费者对于快消品以及生鲜产品的刚性需求，同时借助店商一体的升级路径，为提高配送效率以及精准用户营销，提供了更多的想象空间。”

图9 冲蚀云图Fig.9 Erosion cloud map

由图9可知,气动喷砂喷嘴的冲蚀区域主要集中在收缩管及收缩管与出口段交界处,且在交界面处取得冲蚀速率最大值,为1.05×10-7kg·m-2·s-1；喷嘴入口段与出口段冲蚀情况较小,可忽略不计。

4.3 收缩角度对冲蚀的影响

计算时保持喷嘴收缩段与出口段总长度恒定,通过改变收缩角度,对粒径为0.1～1.2 mm的颗粒在30°、45°、60°收缩角度条件下的颗粒运动特性进行仿真计算。基于材料冲蚀理论,对颗粒撞击壁面较严重的区域进行分析,从而得到冲蚀最严重的位置。颗粒沿压力入口径向均匀分布,运用Lagrange法对其运动轨迹进行追踪。颗粒运动轨迹如图10所示。

图10 不同收缩角度的颗粒运动轨迹Fig.10 Particle motion trajectory at different taper angles

以粒径为0.1 mm的颗粒为例进行分析。

由图10可知,固体颗粒垂直于喷嘴入口端面射入流场,喷嘴入口段内颗粒分布较为均匀,且沿轴向平行流动,由于气动喷砂喷嘴壁面为刚性材料,使得固体颗粒撞击到壁面后发生弹射现象；通过对比不同收缩角度下的颗粒运动轨迹可知,随着收缩角度的增加,颗粒撞击喷嘴内壁的次数在增加,从而使得喷嘴内壁受颗粒的冲蚀作用增强；30°收缩角度的喷嘴冲蚀区域集中在收缩段出口及出口段交界处,60°收缩角度的喷嘴冲蚀区域主要集中在收缩段入口处,即随着收缩角度的增加,喷嘴冲蚀区域由收缩段出口向收缩段入口处逆向发展。

4.4 颗粒粒径对冲蚀的影响

由冲蚀速率计算表达式可知,颗粒粒径的大小是影响喷嘴冲蚀的重要因素之一。颗粒粒径越小,自身惯性力就越小,因此其受连续相的气动阻力影响相对较大；随着颗粒粒径的增加,颗粒自身惯性力增加,从而使固体颗粒携带较大冲击能撞击收缩段壁面造成冲蚀磨损。以三种不同收缩角度的喷嘴为研究对象,取颗粒粒径分别为0.2、0.4、0.6、0.8、1、1.2 mm进行仿真分析。不同粒径的喷嘴最大冲蚀速率变化情况如图11所示。

图11 不同粒径的最大冲蚀速率变化规律Fig.11 Variation law of the maximum erosion rate of different particle sizes

由图11可知,气动喷砂喷嘴的最大冲蚀速率随颗粒粒径的增加呈现先下降后上升的“U”形变化趋势；不同收缩角度的喷嘴最大冲蚀速率变化规律近似相同,但随着收缩角度的增加,喷嘴最大冲蚀速率最低点存在滞后现象,即30°喷嘴的最大冲蚀速率在粒径为0.8 mm时取得最小值,45°喷嘴的最大冲蚀速率在粒径为0.6 mm时取得最小值,60°喷嘴的在颗粒粒径为0.4 mm处取得最小值。

4.5 颗粒质量流率对冲蚀的影响

由图12可知,喷嘴最大冲蚀速率随颗粒质量流率的增加呈现先升后降再升的往复变动趋势；但从总体趋势上看,喷嘴最大冲蚀速率随颗粒质量流率的增加逐渐增大,但并不呈现线性关系；颗粒数量的增加,增大了颗粒撞击喷嘴内壁面的频率及概率,但与此同时颗粒间的相互碰撞造成的能量损失也随之增加,一定程度上减轻了固体颗粒对喷嘴内壁面的冲蚀,因此喷嘴的冲蚀速率随颗粒质量流率的变化才出现往复变动的现象。