基于三剪强度准则的非饱和土库仑主动土压力
2020-02-24雷胜友
崔 舜, 雷胜友
(长安大学公路学院,西安 710064)
土压力计算作为土力学的经典课题,是挡土墙等支挡结构设计的理论依据[1]。为满足工程实践的发展需要,考虑多种因素影响的复杂条件下挡土墙土压力计算被学者所重视,并取得了一些成果[2-7]。在这些研究中,关于岩土体的强度理论,大多应用的是Mohr-Coulomb强度准则,因而忽略了中间主应力σ2对岩土体强度的影响。与此同时,在干旱及半干旱地区的工程实践中,遇到的土体多处于非饱和状态[8],上述研究大多未按照非饱和土理论进行分析,与实际不符,偏于保守。为此,一些学者综合考虑以上因素,将双剪统一强度理论应用于非饱和土压力计算中,进行了有益的尝试[9-11]。然而双剪统一强度理论在特定应力条件下会出现双重滑移角现象与滑移面方向突变的问题,同样考虑中间主应力影响的三剪强度准则[12-13],较好地克服了上述问题,是一个更合理、适用范围更广的强度准则系列。因此,基于三剪强度准则,结合非饱和土抗剪强度理论,推导了多种因素影响的挡土墙库仑主动土压力表达式,通过算例说明了该表达式的合理性,进一步对相关三剪强度参数、非饱和土参数对土压力的影响进行了讨论分析。
1 三剪强度准则及非饱和土抗剪强度
1.1 三剪强度准则
三剪强度准则[12-13]是在双剪统一屈服准则的基础上,考虑了十二面体单元上所有三个主剪应力的共同作用,其表达式如下:
(ασ1-σ3)(σ1-σ3)+b(ασ1-σ2)(σ1-σ2)+b(ασ2-σ3)(σ2-σ3)=(1+b)(σ1-σ3)ft
(1)
式(1)中:α=ft/fc为岩土材料的拉压强度比;σ1、σ2、σ3分别为第一、第二、第三主应力,σ1≥σ2≥σ3,σ2即为中间主应力;b为主剪面应力对(τ12,σ12)和(τ23,σ23)对材料屈服的共同影响系数之和;ft、fc分别为材料的单轴抗拉强度、单轴抗压强度。
对于岩土材料,三剪强度准则可表示为Mohr-Coulomb强度准则的形式[14],便于应用:
τ=σtanφt+ct
(2)
(3)
式中:τ为岩土材料基于三剪强度准则的抗剪强度;φ、φt分别为岩土材料初始内摩擦角、三剪内摩擦角;c、ct分别为岩土材料初始黏聚力、三剪黏聚力;μσ为Lode应力参数,其表示为μσ=(2σ2-σ1-σ3)/(σ1-σ3)。
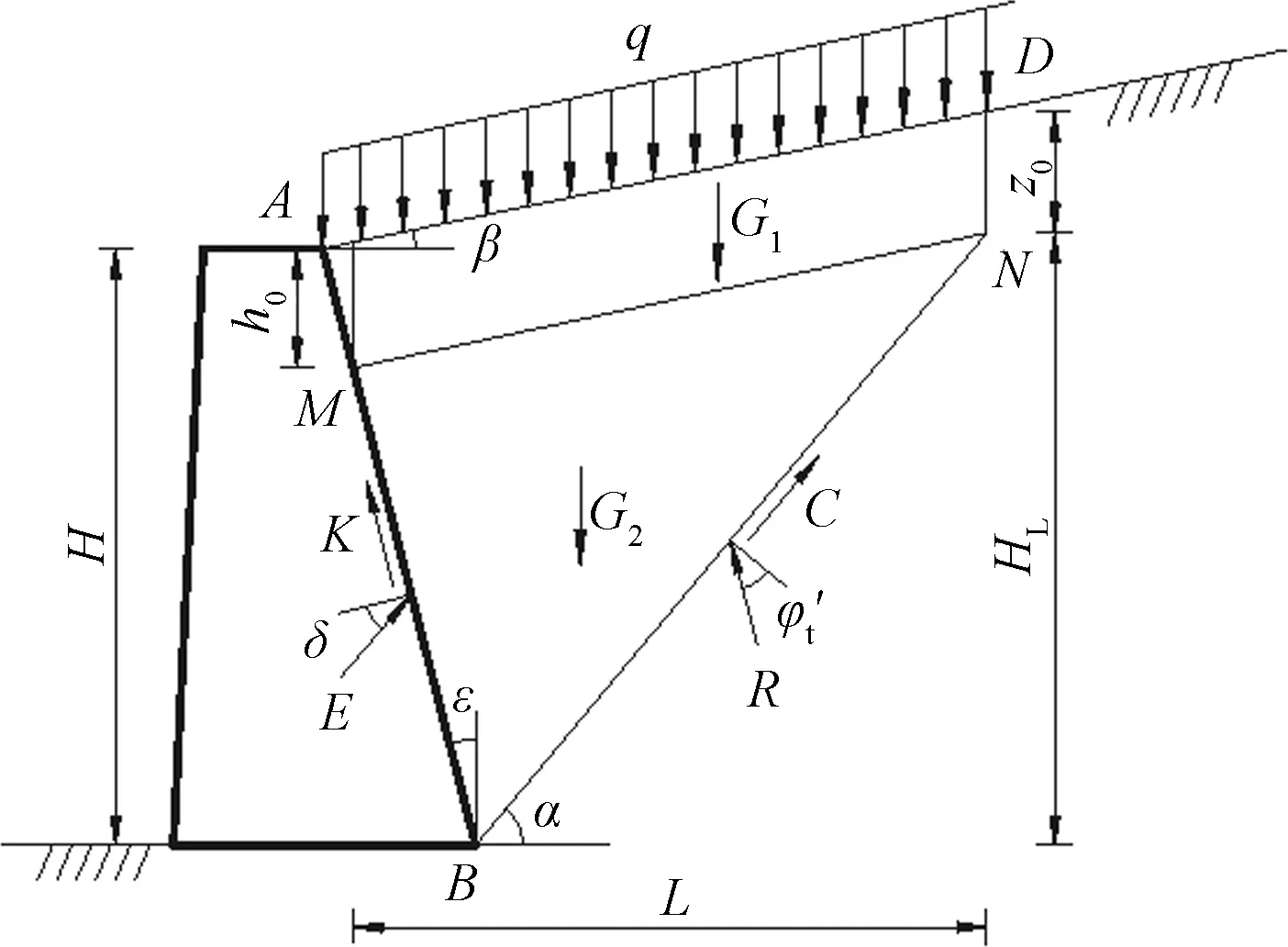
三剪强度准则是一个适用范围较广的强度准则系列,当α=1,b=0时,对应Tresca屈服条件;当α=1,b=1/3时,对应Mises屈服条件;当α<1,b=0时,对应Mohr-Coulomb屈服条件。大量研究结果表明,当α<1,0 挡墙土压力计算与土的抗剪强度理论密切相关。对于非饱和土来说,其抗剪强度理论发展至今,Fredlund提出的非饱和土双应力状态变量抗剪强度公式[2]应用较为广泛,其表达式为 τf=c′+(σ-ua)tanφ′+(ua-uw)tanφb (4) 式(4)中:τf为非饱和土的抗剪强度;c′为有效黏聚力;φ′为有效内摩擦角;(σ-ua)为净法向应力;(ua-uw)为基质吸力;φb为基质吸力角,表示抗剪强度随基质吸力增加的速率。 (5) 还可表示为 (6) (7) 式(5)是一个较完备的土体抗剪强度公式,考虑土体非饱和因素及中间主应力作用,且克服了双剪统一强度理论存在双重滑移角且滑移面方向变化的局限,适用范围较广。当b=0,(ua-uw)=0时,式(5)即退化为Mohr-Coulomb强度准则。 在以下分析中,将挡土墙土压力求解视为平面应变问题。假定墙后填土为均质土,沿深度方向基质吸力均匀分布,基质吸力角保持一致;填土强度特性以基于三剪强度准则的非饱和土抗剪强度公式表示;填土在主动极限平衡状态下,滑裂体为刚体,滑裂面为平面。主动土压力计算分析示意如图1所示,挡土墙墙高为H,滑裂体为BMN,滑裂面BN的垂直距离为HL,滑裂体顶部MN的水平距离为L。由几何关系可得: (8) 式(8)中:ε为挡土墙背面与垂直方向的夹角;β为墙后填土倾斜与水平方向夹角;α为滑裂面BN与水平方向夹角;k为墙后填土与墙背间的黏聚力,δ为摩擦角;ct为填土三剪总黏聚力;φ′t为三剪有效内摩擦角;z0为填土表面裂缝深度;h0为挡土墙顶面到墙背法向接触应力零点的深度,根据几何关系[5],z0可表示为 (9) 图1 主动土压力计算分析示意图Fig.1 Sketch of calculation and analysis of active earth pressure 对滑裂体BMN进行受力分析,各作用力如下。 (1)填土顶部均布荷载Q及裂缝区土体重力G1,表示为 Q+G1=(q+γz0)L=(H-h0)× (10) (2)滑裂体BMN自重G2,表示为 (11) (3)滑裂面BN黏聚力合力C,表示为 (12) (4)挡土墙墙背与填土间黏聚力合力K,表示为 (13) (5)挡土墙墙背对滑裂体作用反力,即所求主动土压力E。 (6)土体对滑裂体作用反力R。 由水平方向平衡条件∑Xi=0,得: (14) 由垂直方向平衡条件∑Yi=0,得: (15) 联立式(14)、式(15),E可表示为 (16) 其中 (17) 根据库仑土压力理论,挡土墙后土体沿滑裂面滑动,必有一滑裂面使滑裂体对挡土墙的土压力为最大值,此滑裂面即为最危险滑裂面,其与水平方向的夹角为滑裂角αa。因此,求取主动土压力前需先求得滑裂角αa。 对于Kq,经三角函数变换,有: (18) 得到Kq表达式: (19) 同理可得 (20) 对式(16)加以处理,使之便于后续求解滑裂角: (21) 其中: (22) 对式(21)通分,得到: (23) 其中: (24) (25) 由前述定义,滑裂角表示为 αa=arccotλ*+β (26) 将式(26)代入式(16)中,得到基于三剪强度准则的非饱和土库仑主动土压力表达式: ct(H-h0)Kac-k(H-h0)Kak (27) 挡土墙的土压力计算问题可视为平面应变问题,因此应用式(27)计算时三剪强度准则参数μσ值取0。式(27)是一个较完备的求解挡土墙主动土压力表达式,可考虑岩土材料中间主应力作用,根据其材料差异选用合适的强度参数,还可考虑其非饱和因素,同时体现填土黏聚力、墙背倾斜、填土面倾斜、填土表面超载及裂缝深度等对土压力的影响。当b=0时,其退化为基于Mohr-Coulomb强度准则的非饱和土库仑主动土压力表达式;当(ua-uw)=0时,其退化为基于三剪强度准则的饱和土库仑主动土压力表达式;当b=0,(ua-uw)=0时,其退化为基于Mohr-Coulomb强度准则的饱和土库仑主动土压力表达式。 式(27)中h0可令土压力分布强度为零得到,求解过程如下: 对式(27)关于H求导,得到: (28) (29) (30) (31) 令ea=0,得到: (32) 由于土压力计算系数Kaγ、Kaq、Kac、Kak均是h0的函数,因此需通过式(32)迭代求解得到h0。经编制程序试算,两次迭代就可得到较精确值。 算例1:某挡土墙高H=8 m[11],填土重度γ=18 kN/m3,有效黏聚力c′=5 kPa,有效内摩擦角φ′=22°,超载q=0,基质吸力角φb=14°,其余计算参数ε、β、δ、k均为0。 由于文献[11]中非饱和土压力解强度准则参数与本文解意义不同,仅选取强度准则参数b=0进行计算对比。表1列出了b=0时不同基质吸力的非饱和土压力计算结果,可以看出,在不同基质吸力条件下,非饱和土压力解计算值与文献[11]解保持一致,证明了本文解的推导是合理的。文献[11]解与本文解均考虑了中间主应力效应,同时本文解可克服双剪统一强度理论存在双重滑移角且滑移面方向变化的局限,并且能得到滑裂角具体数值。 算例2:某非饱和黄土垂直高边坡[15-16],高H=14 m,γ=14.2 kN/m3,c=18 kPa,φ=25°,超载q=0,参数ε、β、δ、k为0。边坡浸水渗透后破坏,经非饱和三轴试验得到c′=4.46 kPa,φb=11.7°,φ′=22.82°,土体基质吸力取浸水末期所测值,(ua-uw)=150 kPa。 采用本文解与朗肯土压力理论分别计算该垂直高边坡土压力,并与土压力实测值进行比较,列于表2。可以看出,计算值均远小于朗肯土压力理论计算结果,且与土压力实测值更为接近。当b=1/3时,计算值略小于实测值,实际应用时,合理确定土体的三剪强度参数是必要的。 表1 算例1本文解与文献[11]解计算值对比Table 1 Comparison in calculated value of example 1 between this paper and ref.[11] 表2 算例2本文解与朗肯理论计算值及实测值对比Table 2 Comparison between the test value and the calculated values using this method and Rankine theory for example 2 以文献[2]算例为基础,增加参数进行计算分析,着重考虑非饱和土抗剪强度参数及三剪强度准则参数对于土压力的影响。某挡土墙高H=10 m[2],γ=18.6 kN/m3,φ′=24°,超载q=0,增加的参数有:α=5°,β=10°,δ=10°,c′=10 kPa,k=5 kPa,φb=12°,(ua-uw)=20 kPa。 图2曲线反映了基质吸力(ua-uw)及三剪强度参数b对土压力Ea的影响。 由图2可知,当基质吸力(ua-uw)一定时,土压力计算值Ea随三剪强度参数b的增大而减小。当(ua-uw)=20 kPa时,b值从0增大到1/3,土压力Ea则从266.0 kN/m减小到201.7 kN/m,减小幅度为24.2%。因此应用三剪强度准则,可有效利用岩土体自身强度,在工程设计时避免过大安全储备造成材料浪费,使工程造价过高。当三剪强度参数b一定时,随基质吸力的增大,土压力计算值Ea呈非线性减小趋势,且基质吸力越小时,减小速率越快。当b=1/6时,(ua-uw)从0增大到80 kPa,土压力Ea从275.9 kN/m减小到119.5 kN/m,减小幅度达56.7%。可见基质吸力的存在及变化,对土压力计算值影响较大,在计算土压力时需要明确土体性质,并精确测定基质吸力大小。 图3曲线反映了基质吸力角φb及三剪强度参数b对土压力计算值Ea的影响。 图2 (ua-uw)、b对Ea影响Fig.2 Impact of (ua-uw) and b on Ea 图3 φb、b对Ea影响Fig.3 Impact of φb and b on Ea 由图3可知,当基质吸力角φb一定时,土压力计算值Ea也随三剪强度参数b的增大而减小。在实际应用中,选取与岩土材料相匹配的强度准则参数是必要的。当三剪强度参数b一定时,土压力计算值Ea随基质吸力角φb的增大而线性减小,当b=1/6时,φb从0增大到21°,土压力Ea从275.9 kN/m减小到197.2 kN/m,减小了28.5%。相对基质吸力来说,基质吸力角对非饱和土压力的影响程度略小,但土体非饱和因素的影响不可忽视,须对其予以重视。 (1)基于三剪强度准则,结合非饱和土抗剪强度理论,推导得到考虑多种因素影响的挡土墙库仑主动土压力表达式。该式更合理地反映了岩土体中间主应力作用,考虑其非饱和因素,可用于较复杂情况下的土压力计算,经算例验证其推导是合理的。 (2)土压力计算值随着三剪强度参数b的增大而减小。选取与岩土材料相匹配的强度准则参数,合理考虑中间主应力作用,可有效利用岩土体自身强度,优化设计,提高经济效益。 (3)非饱和土压力随基质吸力的增大非线性减小,而随基质吸力角的增大呈线性减小趋势,基质吸力对非饱和土压力影响尤为显著。在工程实践中,应明确土体性质,对土体非饱和因素予以重视。1.2 非饱和土抗剪强度
1.3 基于三剪强度准则的非饱和土抗剪强度


2 基于三剪强度准则的非饱和土库仑主动土压力公式推导


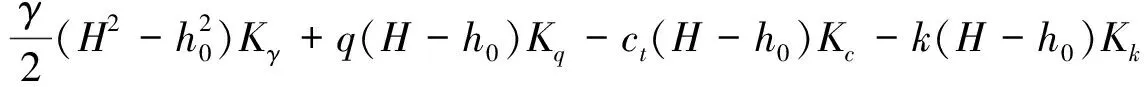

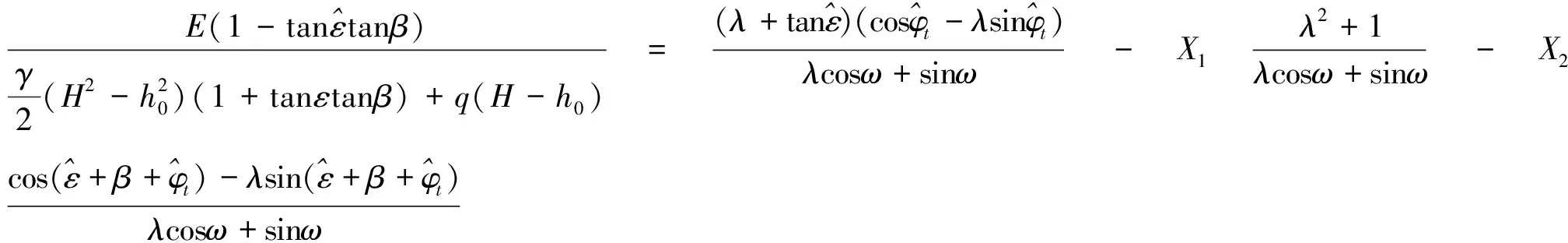



3 算例分析


4 影响因素讨论


5 结论
