摩擦与滚阻对被动行走器步态影响的研究1)

郑 鹏 王琪 吕敬 郑旭东

(北京航空航天大学航空科学与工程学院，北京 100083)

引言

1990年，学者McGeer首次提出了“被动行走”(passive dynamic walking)的概念，描述了一类可以仅依靠自身重力以及结构特性在斜坡上实现稳定行走的机构[1].相比于具有复杂驱动与控制的双足机器人，被动行走器具有能量利用率高，行走步态自然的优点，因此在实验研究和理论研究层面都得到了广泛的关注.目前在实验研究层面已经取得了较多研究成果[2-9].例如，2005 年由美国康奈尔大学、荷兰代尔夫特理工大学、美国麻省理工大学开展的(准)被动行走器的研究工作发表在Science杂志上，简要介绍了被动行走器的实验研究进展，和基于被动行走机制改善双足机器人能效性的实验尝试[2].国内高校，诸如清华大学[3-4]、浙江大学[9-10]等高校的学者也开展了(准)被动行走器的实验样机研究工作.上述研究中的部分(准)被动行走器样机如图1 所示[6-8].

图1 被动(或准被动)双足行走器Fig.1 Passive(or quasi-passive)bipedal walkers

在理论研究层面，最初学者们将接触状态时足与地面间的约束视为铰链，研究了直腿点状足、直腿圆弧足、含膝关节点状足、含膝关节圆弧足等几种不同平面构型的被动行走器.其中Garcia,Asano 等[11-15]以直腿点状足模型被动行走器为对象，研究了被动行走器的不同斜面坡度下的行走效率和稳定性.Gritli 等[16-20]研究了直腿点状足被动行走器在斜面坡度变化下丰富的非线性行为.

近年来，部分学者通过引入法向接触力模型与摩擦力模型描述圆弧足被动行走器足与地面间的接触力，通过数值仿真研究了平面圆弧足直腿被动行走器的步态，得到了支撑足与地面间有滑动或有弹起的步态[21-24].如段文杰等[24]利用牛顿碰撞恢复系数与库伦干摩擦模型描述支撑足与地面间的接触，采用时间步进法[25]分析了摩擦系数与碰撞恢复系数引起的圆弧足被动行走器行走步态的变化.祁峰等[23]利用扩展的赫兹接触模型与修正的库伦摩擦模型描述支撑足与地面间的法向接触力与切向摩擦力，研究了圆弧足直腿被动行走器在不同接触参数条件下的步态变化.郑旭东等[22]利用扩展的赫兹接触模型与库伦干摩擦模型描述支撑足与地面间的法向接触力与切向摩擦力，基于线性互补[26-28]研究了圆弧足被动行走器的多种步态，弥补了原有模型中不能描述静摩擦力的不足.上述研究中尚未考虑圆弧足与地面间的滚动摩阻，滚动摩阻对被动行走器的动力学行为有何种影响是一个值得研究的问题.

综上所述，基于不同假设的研究都取得了一些有意义的研究进展，但也存在一定的局限性.例如，基于足与地面铰接模型的研究方法无法揭示被动行走器足的弹起或滑动过程；基于修正的库伦摩擦模型的研究方法难以仿真被动行走器静止站立的工况；基于库伦干摩擦模型的研究方法须用到试算法，或线性互补算法，这两种算法计算成本较高且繁琐；另外，忽略足与地面间的滚动摩阻是否合理尚需做进一步的探讨.为了弥补上述方法中的不足，本文在现有研究成果的基础上，首先采用扩展的赫兹接触模型和LuGre 摩擦模型描述足地间的接触力，并考虑圆弧足的滚动摩阻；然后应用第二类Lagrange 方程建立被动行走器的动力学方程；最后，将通过数值仿真方法分析支撑足与地面间的摩擦和滚动摩阻等非光滑因素对行走器动力学特性的影响.

1 力学建模

1.1 圆弧足被动行走器模型

本文研究的圆弧足被动行走器模型如图2 所示.

设两腿在髋关节H处用光滑柱铰链连接，且分别记为腿1 和腿2，C1,C2分别为两腿质心的位置，该模型的其余参数符号含义为：m1，m2分别为腿1、腿2的质量，J1，J2分别为腿1、腿2 相对质心的转动惯量，l1，l2分别为腿1、腿2 的长度，c1，c2分别为腿1、腿2 的质心与髋关节H的距离，r1，r2分别为腿1、腿2 的圆弧足半径，γ 为斜面与水平面间的夹角，g为重力加速度.

图2 圆弧足被动行走器Fig.2 Passive dynamic walker with round feet

在斜面上建立平面直角坐标系，其中y轴垂直于斜面向上，x轴沿斜面向下，设髋关节H的坐标为(xH,yH)，两腿与y轴的夹角为θ1,θ2(逆时针为正)，该系统的广义坐标可表示为

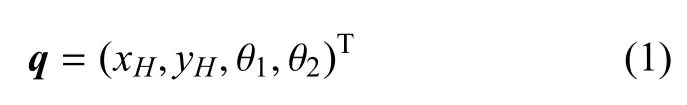
1.2 圆弧足与地面间的接触力建模

圆弧足被动行走器的支撑足i∈{1,2}与地面接触时，会受到法向接触力FNi，切向摩擦力Fsi以及滚阻力偶矩Msi的作用，如图3 所示.

(1)圆弧足i与地面间的法向接触力

圆弧足i与地面间的法向接触力FNi(i=1,2)采用扩展的赫兹接触力模型描述，其表达式为[29]

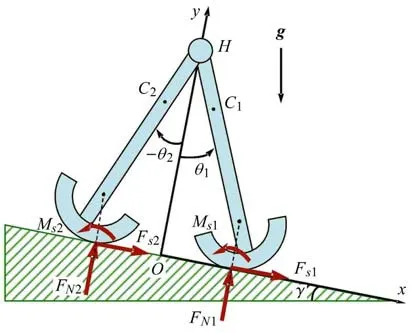
图3 圆弧足受力图Fig.3 Force diagram of round feet

式中，K,χ 分别表示圆弧足与地面间的接触刚度系数与接触阻尼系数，δi表示圆弧足与地面的相对压痕深度，表示圆弧足与地面的相对压痕深度的变化速率.当圆弧足与地面接触时，根据几何关系，δi，(i=1,2)可表示为

(2)圆弧足i与地面间的摩擦力

库伦摩擦模型描述的摩擦力是相对速度的分段连续函数，在相对速度为零时为多值函数，给数值计算带来诸多困难[26].本文采用LuGre 摩擦模型描述支撑足与地面间的摩擦力Fsi(i=1,2).表达式为[30]

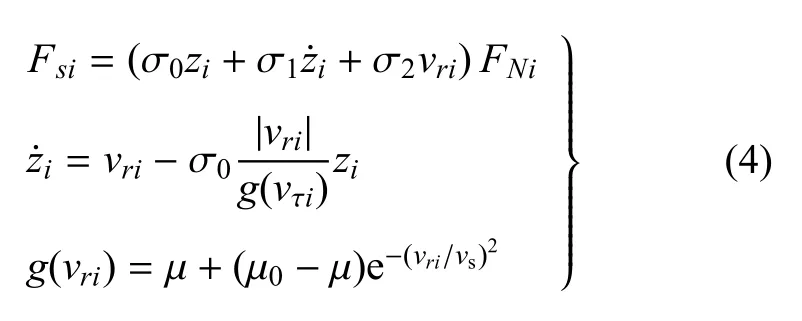
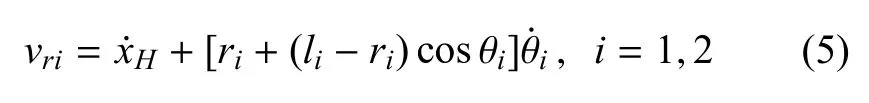
当δi0时，则上式为实际接触点的相对切向速度.

(3)圆弧足i与地面间的滚阻力偶矩

圆弧足被动行走器的支撑足i与地面间的滚阻力偶矩采用下列表达式描述[26]

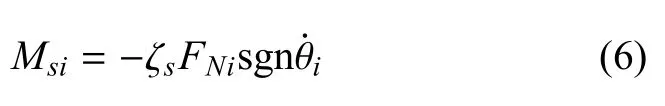
其中，ζs为滚动摩阻系数，为圆弧足i相对地面转动的角速度.

1.3 圆弧足被动行走器的动力学方程

利用第二类Lagrange 方程推导可得被动行走器的动力学方程

其中，Qg,分别表示重力、法向接触力、摩擦力以及滚阻力偶的广义力.上式中各项的具体表达式如下所示

该方程为非线性常微分方程组，可通过数值仿真分析该系统的动力学特性.

2 数值仿真

2.1 算例1 LuGre 摩擦模型参数的选取

LuGre 摩擦模型能够描述诸多的摩擦特性，且具有较好的连续性，目前对于不同材质的物体，该模型中的一些参数不易查找，如σ0和σ1.本文通过数值仿真结果的对比来确定相关参数.为了便于对比，本算例圆弧足被动行走器的参数和运动的初始条件与文献[22]中的相同.

被动行走器参数[22]：m1=m2=1.0 kg，J1=J2=9.6×10−3kg·m2，l1=l2=0.4 m，c1=c2=0.1 m，r1=r2=0.08 m，γ=0.02 rad，g=9.8 m/s2.

接触力参数[22]：K=1.0×106N/m1.5，χ=5.0×107N·s/m2.5，µ=0.40，µ0=0.50，vs=1.0×10−4m/s，σ2=0 s/m，ζs=0 m.

初始条件[22]：xH=0.0 m，yH=0.395 0 m，θ1=0.165 5 rad，θ2=−0.247 9 rad，=0.4971 m/s，=0.048 6 m/s，=−1.256 5 rad/s，=0.005 2 rad/s，z1=0 m，z2=0 m.

取不同的σ0,σ1值进行仿真，将数值结果与文献[22]中采用库伦干摩擦时的数值结果比较.数值结果表明：当σ0=1.0×106m−1，σ1=时，两者的数值结果吻合得很好，如图4 所示.

图4(a)为圆弧足被动行走器的腿1 与y轴夹角θ1的相图，图4(b)为图4(a)中局部区域D1 的放大图.虚(红)线为LuGre 摩擦模型的数值结果，实(蓝)线为库伦干摩擦模型的数值结果，二者的差异很小.说明在该参数条件下LuGre 摩擦模型用于描述被动行走器支撑足与地面间的摩擦是可行的.

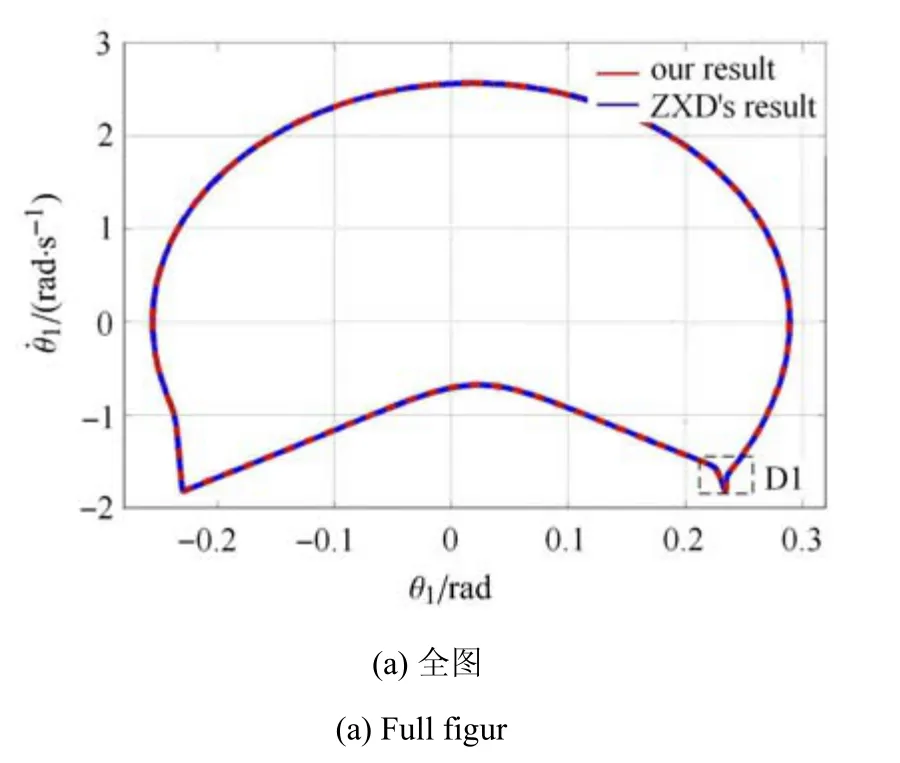
图4 θ1的相图Fig.4 Phase diagram of θ1

图4 θ1的相图(续)Fig.4 Phase diagram of θ1(continued)

2.2 算例2 被动行走器的黏滞与滑移现象

在适当参数条件下，被动行走器在行走过程中会发生黏滞与滑移现象.本文中算例的仿真参数及初始条件如下，未列出的参数和算例1 相同.

系统参数：µ=0.15，µ0=0.20.

初始条件为：xH=0.0 m，yH=0.399 1 m，θ1=0.032 9 rad，θ2=0.017 0 rad，=0.236 2 m/s，=0.006 0 m/s，=−0.590 9 rad/s，=2.386 2 rad/s，z1=0 m，z2=0 m.

通过数值仿真，图5(a)给出了圆弧足被动行走 器的腿1、腿2 与y轴夹角θ1，θ2的相图；图5(b)为vr，FN，Fs的时间 历程图，图5(c)为图5(b)中局部区域D 的放大图.在图5(c)中标注为slip 的区间，支撑足与地面接触时发生打滑；在图5(c)中标注为stick 的区间，支撑足与地面间无滑动，为黏滞状态；在图5(c)中标注为no contact 的区间，表示腿部处于非接触摆动状态.

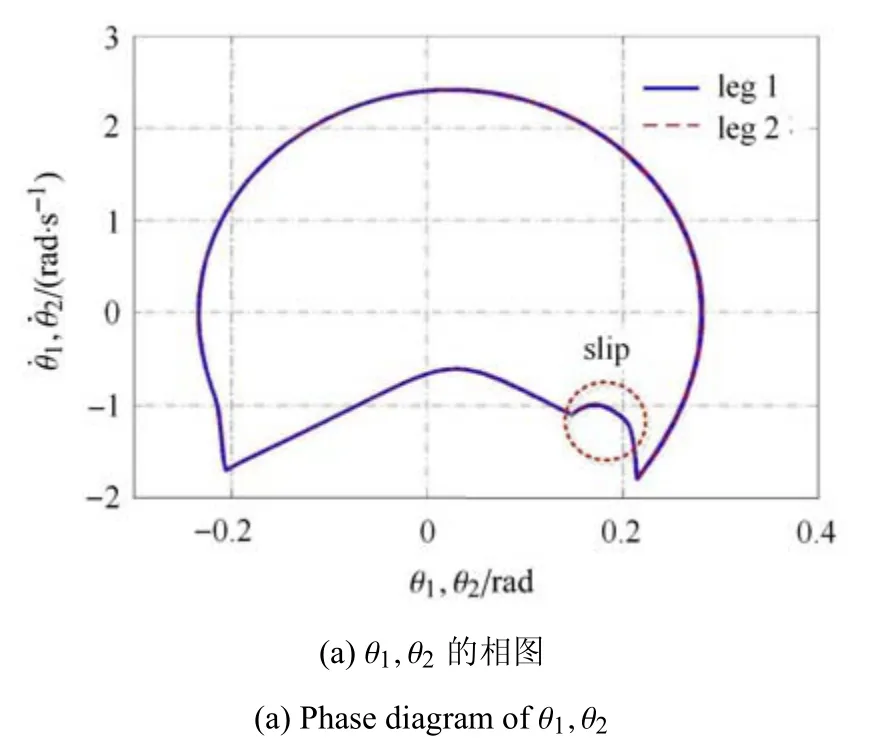
图5 被动行走器的黏滞与滑移现象Fig.5 Stick-slip phenomenon of passive walker

可以看出，LuGre 摩擦模型可以很好地描述被动行走器的支撑足与地面间的滑动摩擦力和静摩擦力.

2.3 算例3 动摩擦系数对被动行走器步态的影响

文献[16-20]中指出：斜面倾角的变化会导致2-连杆被动行走器的产生倍周期分岔或混沌运动.文献[23]中在研究圆弧足被动行走器时也发现了这些现象，同时他们还研究了摆动腿质心位置、圆弧足半径、圆弧足与地面间的接触刚度和接触阻尼等参数等对被动行走器动力学特性的影响，如髋关节H点沿斜面的平均速度V、行走一步所用的时间T、步幅A(两腿间的最大夹角)，以及作用于支撑足上的最大法向接触力Fmax等.

在下面的算例中，将通过数值仿真分析圆弧足与地面间的摩擦系数和滚阻系数对被动行走器动力学特性(如：V，T，A和Fmax)的影响.

本算例分析圆弧足与地面间的摩擦系数对被动行走器动力学特性的影响.仿真所用的参数及初始条件如下，未列出参数和算例1 相同.

系统参数：J1=J2=6×10−3kg·m2，γ=0.11 rad，ζs=0 m.

初始条件：xH=0.0 m，yH=0.373 7 m，θ1=0.389 3 rad，θ2=−0.410 9 rad，=0.236 2 m/s，=0.316 2 m/s，=−2.114 1 rad/s，=−0.647 1 rad/s，z1=0 m，z2=0 m.

通过数值仿真发现，当µ <0.352 时，被动行走器会打滑摔倒，难以持续行走；当摩擦系数较大时，被动行走器的行走特征几乎不变.在此，通过数值仿真详细分析动摩擦系数µ∈[0.35,0.40]对被动行走器动力学特性V,T,A,Fmax的影响.仿真时间历程为200 s，取后50 s (稳态解)的数据进行分析，数值结果如图6 所示.

图6(a)∼图6(d)分别给出了被动行走器动力学特性V,T,A,Fmax受动摩擦系数的影响.从图中可以看出，动摩擦系数的变化对这4个量的影响很小，速度在0.75 m/s 附近，周期约0.85 s，腿部摆动幅度约1.125 rad.

图6 V,T,A,Fmax与µ的关系Fig.6 Relationship between V,T,A,Fmaxandµ

摩擦系数对行走器步态的V,T,A,Fmax的影响很小.但进一步的仿真结果表明：当摩擦系数逐步变小时，被动行走器的动力学特性会发生一项更显著的变化(分岔现象).

取圆弧足与地面接触瞬时作为映射截面，图7(a)和图7(b)分别给出了被动行走器双腿与y轴的夹角及其角速度随动摩擦系数变化的分岔图.其中在PD-1、PD-2 所标注的参数下，被动行走器的运动发生倍周期分岔.在PD-1 点处其运动从周期-1 步态变为周期-2 步态，在PD-2 点处其运动从周期-2 步态变为周期-4 步态.

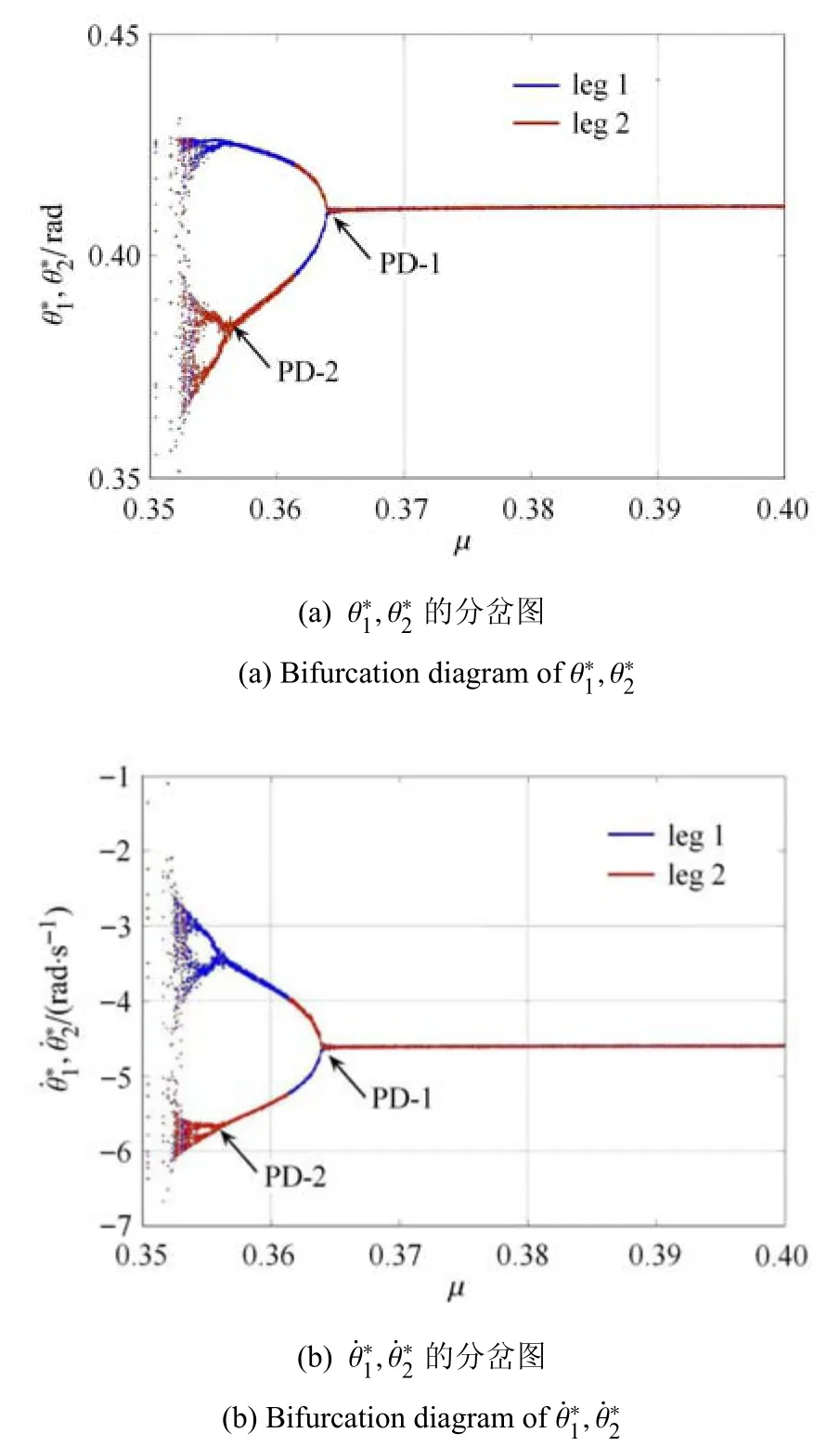
图7 动摩擦系数µ导致的倍周期分岔现象Fig.7 Period-doubling bifurcation caused by the dynamic friction coefficientµ

通过数值仿真，图8 给出了动摩擦系数µ分别为0.38，0.36 和0.354 时被动行走器髋关节纵坐标yH的相图.可以看出：当µ=0.38 时，被动行走器具有无滑动的周期-1 步态，如图8(a)所示；当µ=0.36 时，该被动行走器具有单腿有滑动的周期-2 步态，如图8(b)所示；当µ=0.354 时，该被动行走器具有单腿有滑动的周期-4 步态，如图8(c)所示.其中图8(b)与图8(c)中红色线框区域为发生打滑区域.这是由于当摩擦系数减小，圆弧足与斜面间的接触点无法提供足够的摩擦力，发生打滑，导致了腿1、腿2的运动不一致，存在“大小步”现象.

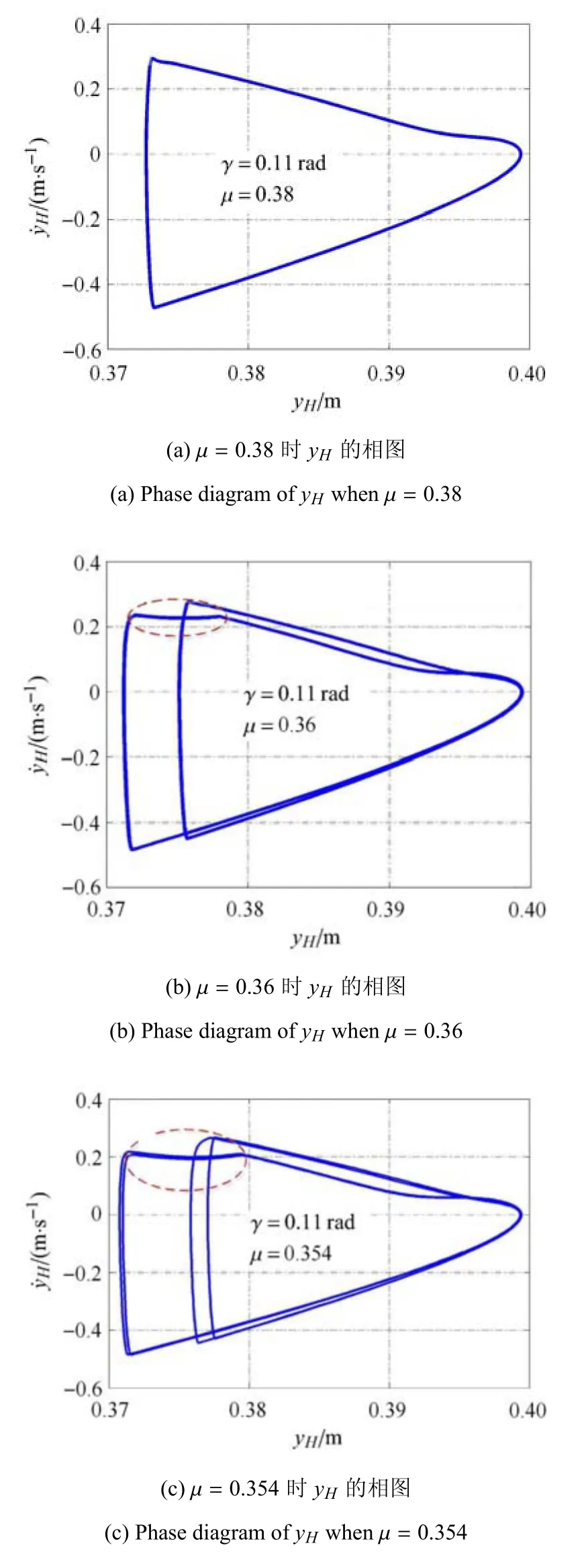
图8 髋关节H 点纵坐标yH 的相图Fig.8 Phase diagram of yH

2.4 算例4 滚阻系数对被动行走器步态的影响

本算例分析圆弧足与地面间的滚阻系数对被动行走器动力学特性的影响，部分仿真参数如下，未列出的参数同算例1 中对应参数.

系统参数：J1=J2=9.6×10−3kg·m2，γ=0.02 rad，µ=0.40，µ0=0.50.

初始条件：xH=0.0 m，yH=0.395 0 m，θ1=0.165 5 rad，θ2=−0.247 9 rad，=0.497 1 m/s，=0.048 6 m/s，=−1.256 5 rad/s，=0.005 2 rad/s，z1=0 m，z2=0 m.

在本算例中，圆弧足与地面间的滚阻系数的取值范围为ζ∈[0.0 mm,5.0 mm].设定仿真时间200 s，取后50 s(稳态解)的数据进行分析.分析结果如图9 所示.

图9(a)给出了髋关节H点沿斜面的平均速度V随滚阻系数的变化曲线，V随滚阻系数的增大而减小；图9(b)给出了每行走一步所用的时间T随滚阻系数的变化曲线，T随滚阻系数的增大而增大；图9(c)给出了步幅A随滚阻系数的变化曲线，A随滚阻系数的增大而减小；图9(d)给出了足地间的最大法向接触力Fmax随滚阻系数的变化曲线，Fmax随滚阻系数的增大而减小.

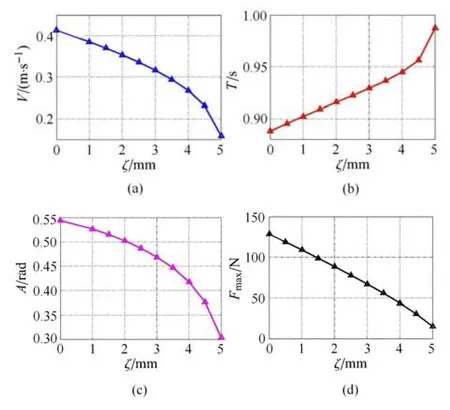
图9 不同滚阻系数下的步态特征: V,T,A,FmaxFig.9 Gait characteristics under different rolling resistance coefficients:V,T,A,Fmax

不同于摩擦系数，滚阻系数对行走器的步态特征(V,T,A,Fmax)的影响很大.下面比较不同滚阻系数下被动行走器的运动状态.

图10(a)和图10(b)分别给出了滚阻系数ζ为0.0 mm,3.0 mm，5.0 mm 时被动行走器髋关节纵坐标yH的相图以及双腿摆动角度θ1,θ2的相图.从图中可以看出，虽然滚阻系数改变了，被动行走器仍以周期-1 的步态行走.只是随着滚阻系数的增大，双腿摆动角的幅值和角速度幅值都逐渐减小.

图10 不同滚阻系数下的(yH,)与(θ,)相图Fig.10 Phase diagram(yH,)and(θ,)under different rolling resistance coefficients

3 结论

本文首先采用扩展的赫兹接触模型、LuGre 摩擦模型以及滚阻模型描述圆弧足与地面的接触力，然后通过第二类Lagrange 方程得到了被动行走器的动力学方程，最后通过数值仿真分析了摩擦系数和滚阻系数对被动行走器的运动特性的影响.本文研究结果表明：

(1)与库伦干摩擦模型相比，采用LuGre 摩擦模型描述足地间的摩擦，可降低判断stick-slip 运动状态的计算成本，易于编程计算，但该模型的某些参数不易获取.

(2)当足地间的摩擦系数较大时，足地接触时无相对滑动，被动行走器的动力学特性不会随摩擦系数的改变而改变，但当摩擦系数较小时，足地间存在stick-slip 切换，摩擦系数的变化对髋关节H点沿斜面的平均速度V、每行进一步所需的时间T、行进步幅A，以及足地间的最大法向接触力Fmax的影响很小；但会改变其步态类型，随着摩擦系数的不断减小，其行走步态会由周期-1 步态变化为周期-2 步态、由周期-2 步态变化为周期-4 步态，当摩擦系数减小到一定程度时，会产生混沌运动或摔倒.

(3)滚阻系数对被动行走器某些动力学特性(V，T，A，Fmax)的影响较大，但在足地间无滑动的情况下，不会改变其行走步态，无倍周期分岔现象.

后续有必要对含膝关节的被动行走器(或欠驱动行走器)进行研究.研究膝关节、髋关节处的非光滑因素对双足行走过程的影响，为双足机器人的设计和精度提高等提供有价值的指导意见.