被均匀流缓慢调制的有限水深毛细重力波1)

李少峰 宋金宝

(浙江大学海洋学院，浙江舟山 316000)

引言

海洋中的波动现象十分丰富.如：海洋表面的波浪、海啸、潮汐和风暴潮等，这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.Larraza 和Putterman[1]对水槽中表面重力波进行了理论研究，用多重尺度法几乎是直接给出了水波振幅所满足的立方非线 性Schrödinger 方 程(non-linear Schrödinger equation,NLSE)及其孤立波解，但是缺乏严密的推导和论证，也没有考虑表面张力的影响.Djordjevic 和Redekopp[2]考虑到表面张力的作用，导出了有限水深中二维毛细重力波振幅所满足的NLSE，对其解进行了稳定性划分，揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法，可研究不同尺度下波浪的演化，大量学者[3-5]使用这种方法进行水波的研究.也有些学者，如王本仁和魏荣爵[6]曾使用变分法研究水波.不管使用何种方法，诸多学者发展了毛细重力波的动力机制.周显初等[7-8]解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9]研究了两层流体中的毛细重力孤立波.Takuji 等[10]分析了短毛细重力波和长重力波的非线性相互作用，指出了在共振情况下短波和长波之间可以相互转化能量，此时短波的群速度和长波的相速度相匹配.Dias 等[11]详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau 等[12]研究了三维毛细重力波，并与Vanden Broeck 等[13]给出的二维情况作了详细的对比，指出二维和三维有较好的相似性.Kang 等[14]给出了有限水深下，伴有恒定涡度(代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen 等[15-17]使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin 等[18-19]指出在伴有分段涡度分布的条件下，三波相互作用是可能的，然而调制不稳定性是和四波共振作用相一致的.Tiron 等[20]数值计算了毛细重力波之间的相互共振作用.

上述文献虽然均没有考虑到均匀流对波的作用，但对本文关注的波流相互作用研究有重要的指导意义.早期，李家春等[21]考虑深水中二维Stokes波边带不稳定性，通过实验观察发现边带不稳定增长率定性地和理论相一致，且微风会提高增长率，而强风却会抑制.Sedletsky[22]分析了水深对高阶Stocks 波调制不稳定性的影响，指出水深加深时非线性作用加强，小波数情形下调制不稳定会重新稳定.近来，廖波等[23]、李少峰等[24]研究了被线性剪切流缓慢调制的有限水深重力波，这里的剪切流是由均匀流和流的剪切组成的，其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响，发现了顺流增强调制不稳定，而逆流减弱它.Hsu 等[25]分析了被涡度缓慢调制的有限水深毛细重力波，他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外，还有些学者[26-32]研究了不同物理背景下的波流相互作用，如徐祥德等[33]详细介绍了大气中大尺度波流相互作用及波动传播模态；徐俊丽等[34]分析了高频波对定常Ekman 流解的影响；杨衡等[35]、魏艳等[36]、程永舟等[37-38]讨论了波流和结构物的相互作用.

在本文中，基于文献[2]的研究成果及结合文献[23-25]的分析方法，考虑均匀流对毛细重力波的调制作用.在第一节，将使用多重尺度法推导被均匀流调制的二维毛细重力波振幅在有限水深中所满足的NLSE.在第二节，通过使用NLSE，分析被均匀流调制的毛细重力波的不稳定性.第三节是本文的主要结论.由于毛细重力波与流的相互作用可以有效地改变海表粗糙度和海洋上层流场结构，所以这对海面风场、海表压强、海气通量交换等有重要意义.另外，了解海表面的这些短波动力机制，对卫星遥感的精确测量和海气耦合模式的改进等也有重要意义.

1 方程的推导

1.1 控制方程与边界条件

假设流体运动是无黏的、不可压的和无旋的.如图1 所示，考虑均匀流作用下二维毛细重力水波在有限水深中的传播，坐标原点o位于静止水面处，x方向是水波的传播方向，y方向垂直向上与重力方向相反，z垂直纸面向外.这里，把与波动方向一致的均匀流称为顺流，反之称为逆流.故二维水波基本方程组[39-42]可表述为

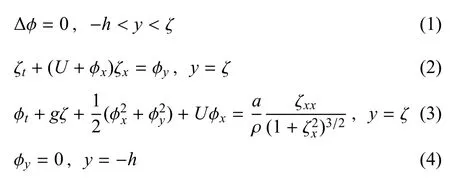
图1 二维毛细重力水波在均匀流作用下的传播.ζ(x,t)是自由面波动，c 是波速度Fig.1 Schematic of the Eulerian framework for two-dimensional propagating capillary-gravity waves with a uniform fl w.ζ(x,t)is the free surface elevation and c is the wave velocity

其中，φ 是速度势函数，U是均匀流为常数，h为流体的深度，ζ 为自由面起伏，g是重力加速度，a为流体表面张力系数，ρ 为流体的密度，∆为二维Laplace 算子.其中下标表示对相应变量求导.式(2)是自由面上的运动学边界条件，式(3)是自由面上的动力学边界条件，式(4)是底边界条件.

1.2 非线性Schrödinger 方程

引入下列多重尺度[2]

其中，波陡ε=kA是度量非线性程度的小参数，k是载波波数，A是振幅，cg是群速度.把式(5)代入式(1)∼式(4)中，得到新的方程组

其中式(4)没有变化.对φ 在y=0 附近按ζ 幂次Taylor 展开，进行线性化处理上边界条件(7)和(8).假设方程组(4)，(6)∼(8)有如下的渐近解

其中，ω 是角频率，n是谐波数，φ−n和ζ−n分别表示φn和ζn的共轭.然后把φn和ζn关于ε 小级数展开

这里j是阶数，假设φ00=ζ00=0.将式(9)和式(10)代入式(4)，式(6)∼式(8)中，得到了前三阶摄动问题的方程组.

(1)εe1(表示一阶一次谐波项)：确定了频散关系

(2)ε2e1：确立了行波的群速度

其中，µ=kh是划分浅水和深水的无量纲参量，一般认为µ>π 属于深水，µ<0.1π 是浅水，介于二者之间是有限水深.同时ζ01=0

其中，D是待确定的慢变量函数.

(3)ε2e2：获得了φ22及ζ22的表达式

(4)ε3e0：得到一个由短波调制产生的平均流动势φ10的长波方程

它描述以波速U±(gh)1/2向左右传播的长波所伴随的参数变化.同时

(5)ε3e1：经过繁琐的计算，由于频散关系，B和Dη被消除了，最终得到了描述波形包络演化的NLSE

式中

它说明在N=σ2/(3-σ2)处毛细重力波发生分叉，是一种Wilton 涟漪现象，在深水情形下，σ=1，N=1/2.另一处是

有量纲形式是

它反映了长重力波与短毛细重力波发生共振，此时短波的群速度与长波的相速度相一致.同样地可以得到自由面ζ 的振幅a所满足的方程

同时有必要考虑在深水情形下NLSE 系数的变化，即µ→∞时

2 稳定性分析

显然式(26)有如下的Stokes 波解

其中a0是初始振幅，考虑在振幅和相位上有小扰动的解

将上式代入式(26)中，线性化Stokes 波解，有

分开上述方程实部和虚部，产生一个关于小扰动的常系数线性方程组

它有如下的解

其中，L和Γ 分别是扰动波数和扰动角频率，将式(32)代入方程组(31)中，式(31)有非零解的充要条件是

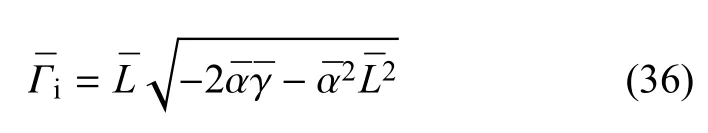
无量纲不稳定最大增长率是

如图2(a)所示，5 条曲线将(N,µ)平面划分为6 个区域，其中“S”表示Stokes 波解是调制稳定的，而“U”表示Stokes 波解是调制不稳定的，但是均匀流不影响这个区域的划分.曲线1 和曲线5 表示非线性系数，曲线1 与µ轴的交点为熟悉的µ=1.363，表示在不考虑表面张力时，µ<1.363，重力波是稳定的；µ >1.363，它是不稳定的.曲线2 表示耗散系数，即相速度达到最小值且和群速度相一致.曲线3 和4 是的奇异处，分别表示毛细重力波分叉及长波和短波共振.由式(27)知，曲线2 和3 的渐近线分别是N=2/31/2-1，N=1/2,如图2(b)所示，它们之间毛细重力波是稳定的；长短波共振曲线4 有渐近线

图2 Stokes毛细重力波稳定区域划分Fig.2 Stability diagram for Stokes capillary-gravity waves

曲线5 有渐近线

值得注意的是，毛细重力波在曲线4 和5 渐近线之间是稳定的，但当µ1 时，即深水时，它们在µ轴上的截断3/4 和35/4 可以被忽略，这两条边界线重合在一起(斜率相同)，它们之间稳定区域消失，这也解释了长短波共振在深水中消失的原因[2,25].

2.1 不稳定最大增长率

如图3 所示，知N大致上被划分为4 个部分:[0,0.15]，(0.15,0.5)，[0.5,1.1]，(1.1,+∞)，其中(0.15,0.5)是稳定区域.我们来分析不稳定最大增长率随水深的变化趋势.如图3(a)所示，N=0时，实线与µ轴的交点为µ=1.363，随着N增大，交点µ值变小，体现了调制不稳定的重新稳定；且随着µ变大而变大，逐渐趋于一个常值，亦随着N增大而增大.但在N∈[0.5,1.1]中，如图3(b)所示，随着µ变大而变小，且N越大下降的趋势越快，在深水时达到常值.曲线4 及曲线5 将N∈(1.1,+∞)不稳定区域隔开，所以随µ变化被分为两部分，如图3(c)、图3(d)所示，在µ前半段，随µ增大而逐渐减小到0，随N增大，每条曲线向右边的N=+∞靠近；在µ后半段，亦随µ增大而减小，但趋于一个常值，且随着N增大，曲线向右移动，远离N=+∞.

图3 =0 时，无量纲最大增长率随水深µ的变化Fig.3 Dimensionless maximum growth rateas a function of dimensionless water depthµfor=0

如图4(a)所示，在N前半段，随N增大先减小后增大，且随着水深增大，变化范围变大，逐渐向右偏移；但在N后半段，如图4(b)所示，随N增大而增大，随水深增大而减小且向右偏移.

图4 =0 时，无量纲最大增长率随N 的变化Fig.4 Dimensionless maximum growth rateas a function of N for=0 at differentµ

图5 无量纲最大增长率的变化Fig.5 Dimensionless maximum growth rate

图5 无量纲最大增长率的变化(续)Fig.5 Dimensionless maximum growth rate(continued)

2.2 不稳定增长率

图6 =0 时，无量纲增长率随无量纲扰动波数的变化Fig.6 Dimensionless growth rate as a function of dimensionless perturbation wave number for =0 at different N

图6 =0 时，无量纲增长率随无量纲扰动波数的变化(续)Fig.6 Dimensionless growth rateas a function of dimensionless perturbation wave numberfor=0 at different N (continued)

如图7 所示，与图5 有类似的结果，顺流使无量纲不稳定增长率变小，逆流使之变大，且相差的倍数都是1-.

3 结论

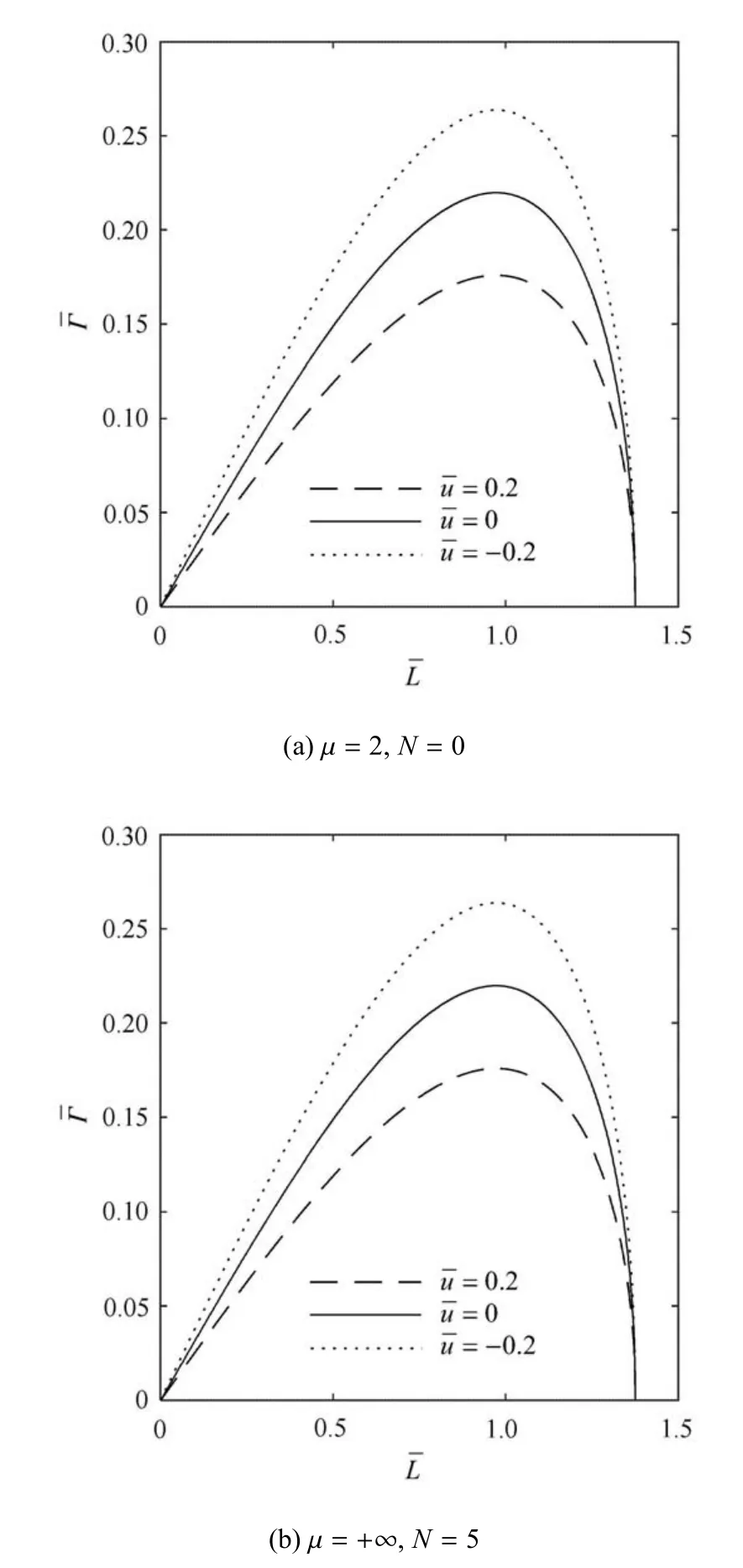
图7 无量纲增长率随无量纲扰动波数的变化Fig.7 Dimensionless growth rate as a function of dimensionless perturbation wave number at different

该文分析了均匀流对毛细重力波的调制作用.从水波基本方程出发，考虑了均匀流的作用，使用多重尺度分析方法导出了毛细重力波振幅所满足的NLSE.通过毛细重力波调制稳定性分析，知NLSE 中频散系数α 和非线性系数γ 同号时，毛细重力波是调制稳定的；α 与γ 异号时，它是调制不稳定的，此时会有钟型孤立波的产生.而α 和γ 的大小是与均匀流、水深和表面张力有关的.通过对α 与γ 符号的判断，知α=0 和γ=0 及它们的奇异处5 条曲线将(N,µ)平面划分为6 个区域，从左到右，稳定和不稳定依次交换；在深水时，N轴被划分为3 个稳定和不稳定依次交替的片段，即N∈[0,0.15]∪(0.5,+∞)时，毛细重力波是调制不稳定的；但N∈(0.15,0.5]时，它是调制稳定的.均匀流对这些区域的划分没有影响.同时也得到了微扰动的频散关系，给出了毛细重力波不稳定的增长率及最大增长率随水深、表面张力及扰动波数的变化趋势.指出了顺流会减小增长率及最大增长率，逆流会增加它们.

海洋上界面过程直接影响和调控着海气边界层结构与海气相互作用，特别是发生在海气界面的海洋表面波动在海气相互作用中发挥着重要作用.当风吹过海面时，会在海面产生切应力，这种摩擦应力会使海面形成毛细重力波和重力波，它们与海流的相互作用会有效地改变海表粗糙度和海洋上层流场结构，进而影响海气界面动量、热量及水汽的交换.尽管风浪频谱的主要能量集中于谱峰频率附近，但谱的高频率部分对研究海-气相互作用和海面的反射性能等有重要意义.本文建立了一个关于均匀流与毛细重力高频波相互作用的简单模型，来刻画实际海洋中复杂的海流与高频波的相互作用.了解海表这些短波动力机制，对卫星遥感的精确测量、海气相互作用的深入研究及海气耦合模式的改进等有重要意义.