风速不确定性对风力机气动力影响量化研究1)

2020-02-23唐新姿王效禹袁可人彭锐涛

力学学报 2020年1期

唐新姿王效禹袁可人彭锐涛

(湘潭大学机械工程学院,湖南湘潭 411105)

引言

风力机常年运行于地表大气层中,工作环境非常复杂.由于地表地貌,高度,气候等差异,实际自然来流风速随机波动.风速不确定性造成风力机气动力和载荷分布不确定性,对风电稳定性和可靠性产生严重影响,开展风力机复杂工况下气动不确定性研究对于保障风电系统高效可靠运行具有重要意义.

目前风力机气动载荷研究主要方法有数值计算方法、叶素动量(blade-element momentum,BEM)理论和风洞试验等.其中,叶素动量理论是风力机气动设计普遍采用的方法,该方法应用多基于确定性工况条件.为提高该方法在复杂工况的适应性,国内外学者针对该方法进行了相关改进,包括气动弹性修正[1]、动态失速修正[2]、三维效应修正[3-7]、阻力修正[8]和风切变修正[9]等,这些修正使得BEM 应用更为广泛,但不确定工况问题仍然有待解决.针对风电不确定性,国内外学者在预测模型[10],控制策略[11-15]和翼型[16-22]等方面开展了相关研究.考虑风速变化,Keshavarzzadeh 等[23]结合Von Karman 模型和非嵌入式混沌多项式将风速表示为时间、半径和随机变量的函数,基于叶素动量理论和牛顿迭代法提出水平轴风力机叶片不确定性优化方法.Murcia 等[24]构建四维湍流空间,提出在多种不确定湍流参数下预测风力机气动性能方法.Antonini 等[25]基于四种湍流模型并对数值模拟结果进行加权处理,揭示考虑风向不确定性的重要性.Toft 等[26]基于加速因子和风力机与测量位置之间距离建立风速不确定性概率模型以评估风力机结构疲劳载荷.Horna 等[27]研究了风速和风向不确定性以及环境载荷不确定性对海上风力机地基疲劳可靠性的影响.Yan 等[28]提出一种包含桨矩角和风向参数的风力机功率曲线模型描述能量转化不确定性.

复杂工况下风力机气动力研究本身是具有挑战性的研究热点问题,不确定问题正受到国内外学者重点关注.采用数值模拟或风洞试验方法进行工况不确定条件下风力机气动力研究将非常复杂且工作量巨大.本文提出一种基于修正叶素动量理论和非嵌入式概率配置点法的风力机不确定气动计算方法,建立水平轴风力机不确定性空气动力学响应模型;基于该模型,以NREL Phase VI S809 风力机为研究对象,量化不确定工况下随机气动边界条件对风力机气动力的影响程度;从气动诱导上揭示不确定性在叶片展长方向上的传播机制,为风力机设计与应用提供理论依据和重要参考.

1 不确定风力机气动力学计算模型

1.1 修正叶素动量理论

目前描述风轮作用力与来流速度之间的关系主要有考虑尾涡旋转的修正叶素动量理论.该理论认为,当气流作用在风轮上产生转矩时,气流同样会受到风轮反作用.风轮对气流的影响用诱导因子表示,叶片截面速度关系如图1 所示.

图1 叶片截面速度示意图Fig.1 Velocity of blade element

根据动量理论,得叶片扭矩Q和推力T为

式中,a为轴向诱导因子;b为周向诱导因子;r为叶素半径,m;ρ 为空气密度,kg/m3;V1为来流风速,m/s;Ω 为叶轮转速,r/min;α 为攻角,(◦);β 为桨矩角,(◦).

根据叶素理论,同样得到叶片扭矩Q和推力T为

式中,B为叶片数;c为弦长,m;Cl为翼型升力系数;Cd为翼型阻力系数;W为相对风速,m/s;ϕ 为入流角,(◦).其中,相对风速、来流风速与叶轮转速的关系为

动量理论和叶素理论结合得

式中,Ct为叶素切向力系数;Cn为叶素法向力系数;σ 为风轮实度,σ=Bc/(2πr).

当轴向诱导因子a>0.38 时,根据Wilson 和Prandtl 方法进行修正

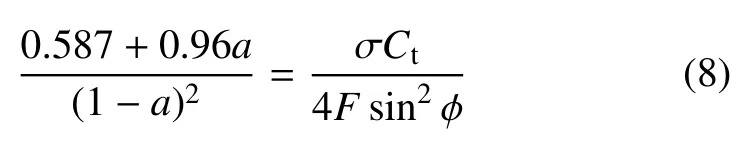
其中F为叶尖和轮毂损失修正.

叶尖损失修正系数Ftip为

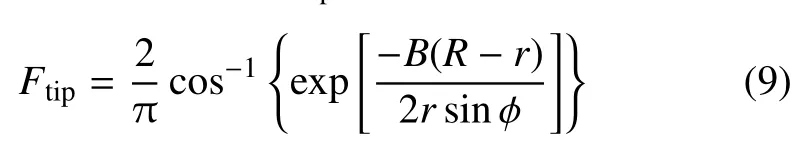
轮毂损失修正系数Fhub为

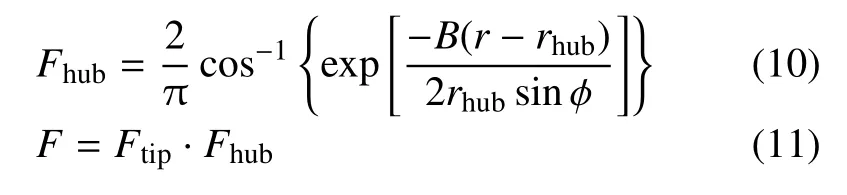
式中,Ftip为叶尖损失;Fhub为轮毂损失;R为叶片半径,m;r为叶素半径,m;rhub为轮毂半径,m.

修正后轴向诱导因子为

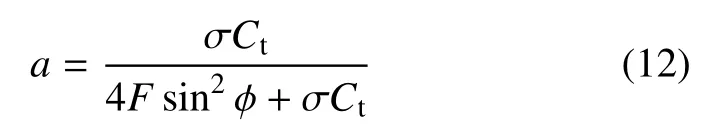
修正后周向诱导因子为

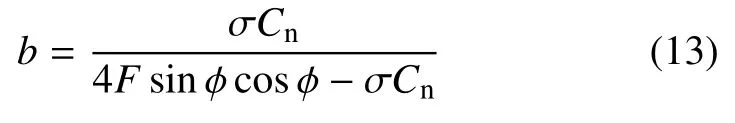
通过式(12)和式(13)求解每个半径位置上周向和轴向诱导因子描述风力机准三维流场变化,进而得到风力机气动力.

1.2 非嵌入式概率配置点法

本文将风力机气动力计算方法和非嵌入式概率配置点法 (no-instrusive probabilistic collocation,NIPRC)结合,进行不确定气动力计算.NIPRC 是混沌多项式法对随机变量进行多项式展开形式变换和随机配置点法的结合.随机变量ϕ(x,t,θ)是关于时间t,空间x和随机变量θ 的函数,其表达式为

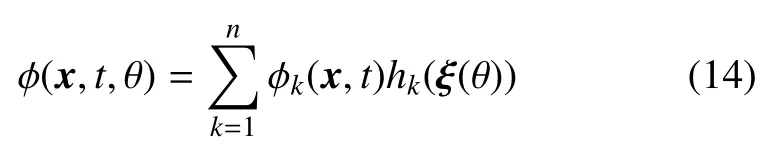
式中,ϕk(x,t)是随机变量ϕ(x,t,θ)在配置点θk的解,是由确定性计算获得,hk表示与该点对应的拉格朗日差值多项式,是通过n个配置点的n-1 阶多项式,该多项式表达式为

式中,hk(ξ(θi))=δki是和配置点对应的拉格朗日差值多项式,n为配置点个数.

考虑到风速为自然随机等特点,随机性符合正态分布,因此本文配置点采用随机空间Ω 上对ϕ(x,t,θ)积分的高斯积分点,其表达式为

式中,xk是和权函数ρ(x)对应的正交多项式的零点,即高斯点;w(x)是各高斯点对应的求积系数.

对于高斯分布随机变量,其概率密度函数为

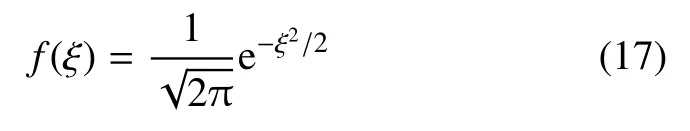
与其对应的Hermite 多项式的权函数为

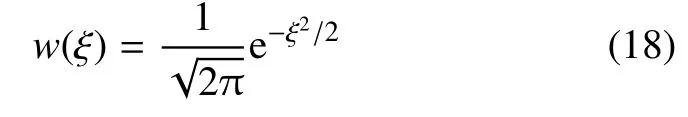
对应高斯积分为Gaussian-Hermite 积分,高斯积分点即为n次Hermite 多项式的n个零点,对应的求积系数即为权重.其具体表达式为

在各个配置点进行确定性分析之后,根据统计学中均值和方差的定义,推导出均值和方差的计算公式,得到不确定风速对于气动力的影响,具体表达式为

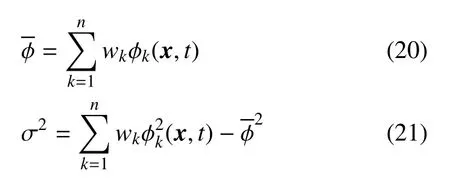
2 研究对象及方法验证

NREL Phase VI 风力机[29]为三叶片失速调节风力机,叶片为扭曲锥形,基于S809 翼型设计,叶片半径为5.03 m,额定功率为20 kW,锥角为3.4◦,转速为72 r/min.叶片轮毂长度为0.724 m,从0.724 m 处的轮毂到S809 翼型之间为线性过度.该风力机模型由美国国家航空航天局基于24.4 m×36.6 m 风洞进行空气动力学实验.

首先基于修正叶素动量理论建立确定性风力机气动模型,编制MATLAB 程序进行风力机气动分析.图2 为功率和推力计算曲线和实验曲线对比.由图可知,功率和推力计算值与实际测量值基本吻合,验证了本文所建立气动模型的正确性.

根据自然风速统计规律,假设随机风速服从高斯分布,采用非嵌入式概率配置点法结合修正叶素动量理论进行不确定性分析,计算流程如图3 所示.首先输入风速工况条件,然后利用NIPRC 方法得到风速配置点及其求积系数,再应用BEM 方法求解风力机气动参数,最后计算输出功率、推力、挥舞弯矩和摆振弯矩,及其均值和标准差.

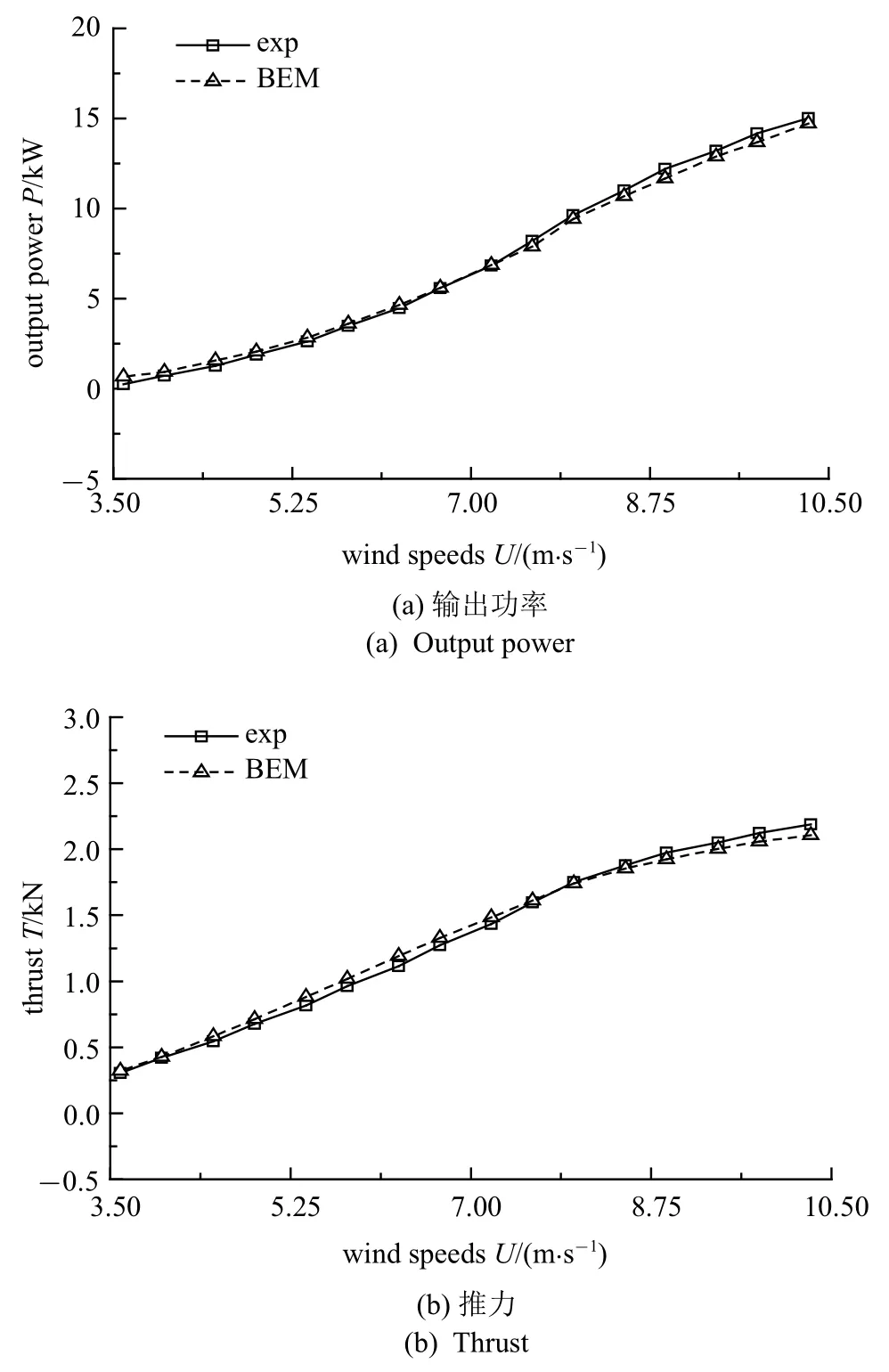
图2 输出功率和推力计算值和实验值对比Fig.2 Comparison of calculated and experimental output power and thrust

图3 不确定性分析计算流程Fig.3 Flow chart of uncertainty calculation

平均风速为7 m/s,考虑到平坦地形大气层常规湍流强度为5%∼15%[30],取标准差为平均值10%.对应一阶、二阶和三阶配置点和权重如表1 所示.

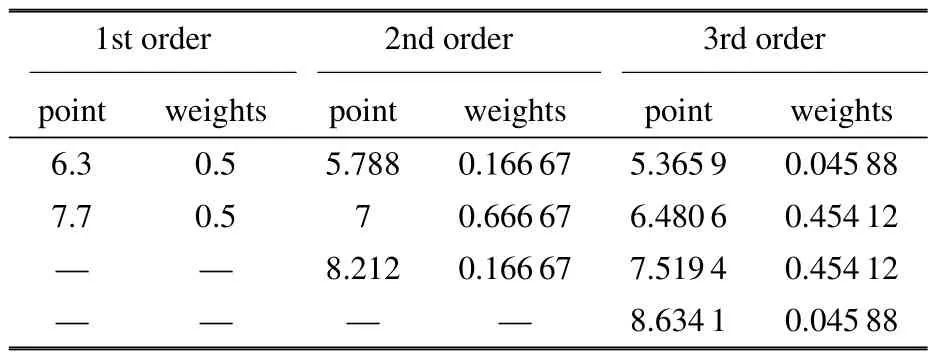
表1 平均风速为7 m/s 的不同阶配置点及其响应的权重Table 1 Different order configuration points with average wind speed of 7 m/s and the weight of their responses

表2 给出了风速为7 m/s 时一阶、二阶和三阶配置点功率和推力计算值对比.二阶和三阶配置点计算结果基本吻合,因此后续基于二阶NIPRC 计算.

表2 不同阶配置点功率和推力的计算值Table 2 Calculated power and thrust with different order configuration points

为验证不确定分析计算模型,采用蒙特卡洛(Monte Carlo,MC)方法进行验证.表3 给出了风速为7 m/s 时采用NIPRC 和MC 计算功率和推力的平均值和标准差对比.采用两种方法计算所得结果基本一致,功率和推力最大误差分别为3.10%和2.81%,验证了不确定分析模型的正确性.

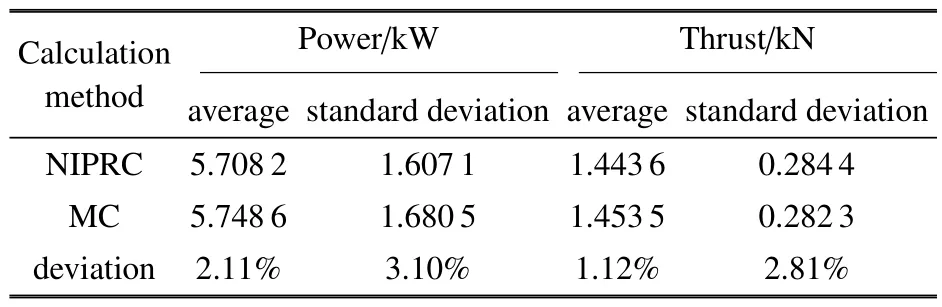
表3 NIPRC 和MC 功率和推力计算值对比Table 3 Calculated power and thrust based on NIPRC and MC

3 结果分析

取5∼9 m/s 五个平均风速,标准差S tD分别为5%,10%和15%倍均值,进行多风速工况多种不确定度对比分析.

3.1 功率和推力

图4 为不同平均风速及标准差下风力机输出功率不确定性对比.相同平均风速不同标准差下输出功率均值基本一致,标准差越大输出功率波动幅度越大.平均风速为7 m/s 输出功率波动达到最大,其中标准差为5%时最大波动幅度为13.44%,标准差为10%时最大波动幅度为24.94%,标准差为15%时最大波动幅度为35.11%.

图4 不同风速及标准差下风力机输出功率不确定性Fig.4 Uncertainty of wind turbine output power under different wind speeds and standard deviations

图5 为不同平均风速及标准差下风力机推力不确定性对比.相同平均风速不同标准差下推力均值基本一致,标准差越大推力波动幅度越大.标准差为5%时,推力的波动幅度在风速为7 m/s 最大,最大波动幅度为8.00%;标准差为10%时,推力的波动幅度在风速为7 m/s 时最大,最大波动幅度为14.96%;标准差为15%时,推力的波动幅度在风速为7 m/s 时最大,最大波动幅度为22.02%.

图5 不同风速及标准差下风力机推力不确定性Fig.5 Uncertainty of wind turbine thrust under different wind speeds and standard deviations

3.2 挥舞弯矩和摆振弯矩

图6 为不同风速及标准差下风力机挥舞弯矩不确定性对比.不同标准差下挥舞弯矩均值基本一致,标准差越大,挥舞弯矩波动越大.三种标准差下挥舞弯矩波动均在风速为7 m/s 时最大,标准差为5%时最大波动幅度为7.20%,标准差为10%时最大波动幅度为13.64%,标准差为15%最大波动幅度为19.90%.

图6 不同风速及标准差下叶根挥舞弯矩不确定性Fig.6 Uncertainty of the flapwise moment of the blade root under different wind speeds and standard deviations

为进一步分析不确定性影响,计算挥舞弯矩在叶片全长上的分布,由图6 分析得到在风速为7 m/s时挥舞弯矩的波动最大,因此选择7 m/s 计算.

图7 为风速为7 m/s 时不同标准差下挥舞弯矩在叶片全长上的分布.三种标准差下均值基本相同,标准差越大挥舞弯矩波动越大.标准差为5%时,挥舞弯矩在r/R为0.83 时波动最大,最大波动幅度为7.01%;标准差为10%时,挥舞弯矩在r/R为0.88 时波动最大,最大波动幅度为13.39%;标准差为15%时,挥舞弯矩在r/R为0.88 时波动最大,最大波动幅度为19.33%.风力机挥舞弯矩波动在叶根部分比较小,在叶尖部分比较大,主要因为弯矩计算受半径影响,而载荷不确定性在叶片全长上变化不大.

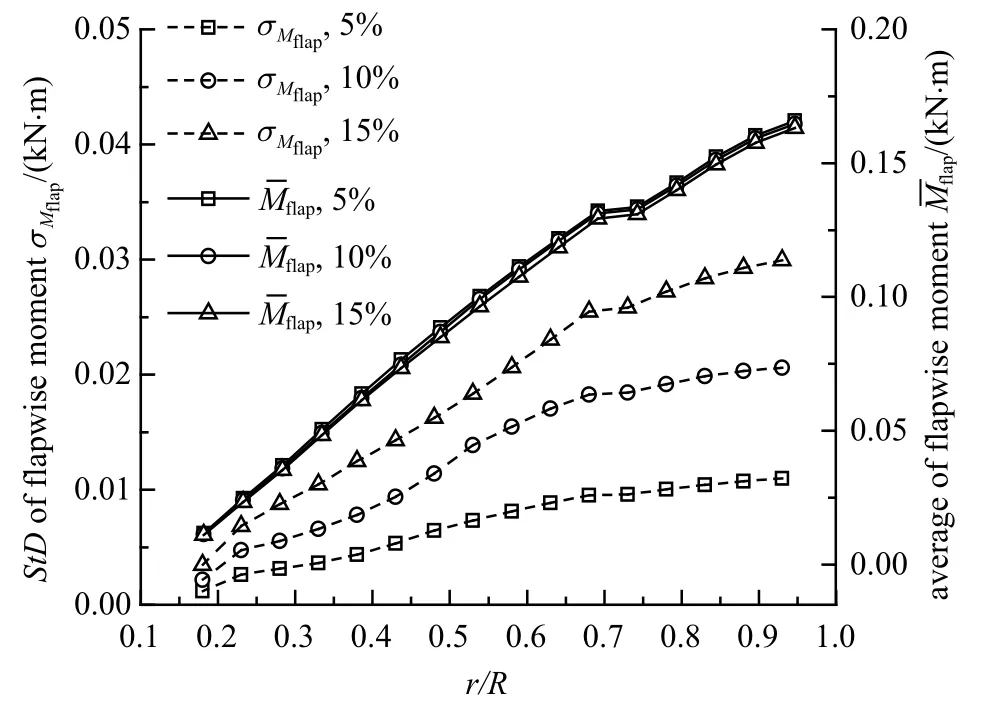
图7 不同标准差下挥舞弯矩在叶片全长上的分布Fig.7 Distribution of flapwise moment on the full length of the blade under different standard deviations

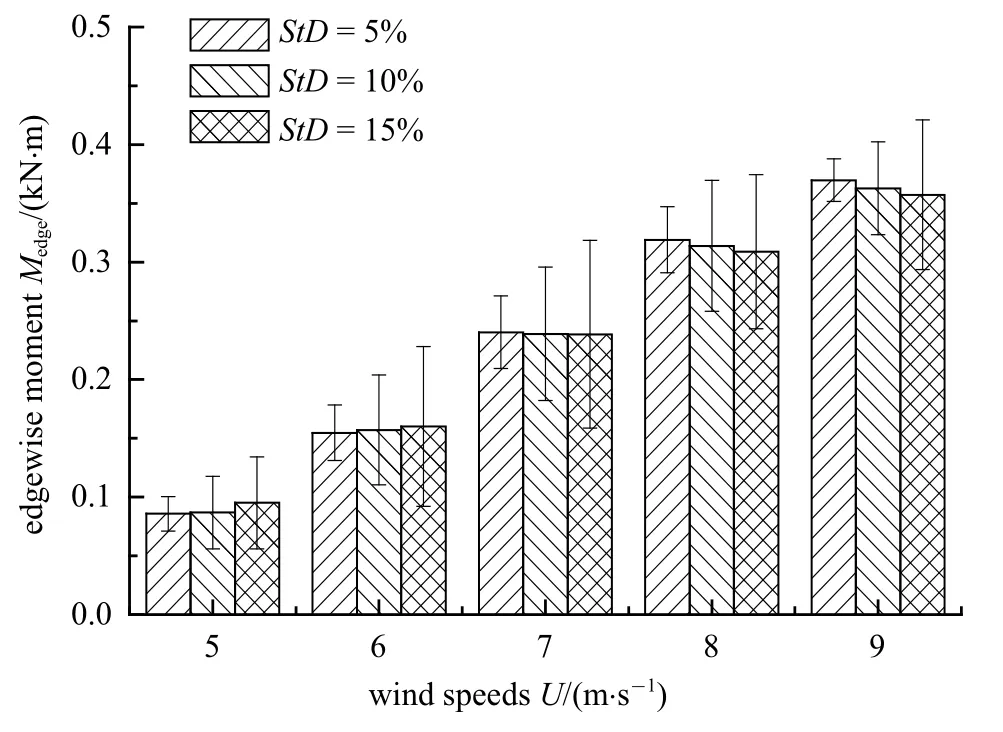
图8 不同风速及标准差下叶根摆振弯矩不确定性Fig.8 Uncertainty of the edgewise moment of the blade root under different wind speeds and standard deviations

图8 为不同风速及标准差下风力机摆振弯矩不确定性对比.三种标准差下摆振弯矩均值基本一致,标准差越大摆振弯矩波动越大.三种标准差下摆振弯矩波动均在风速为7 m/s 时最大,标准差为5%时最大波动幅度为12.84%,标准差为10%时最大波动幅度为23.72%,标准差为15%时最大波动幅度为33.49%.

为进一步分析不确定性影响,计算摆振弯矩在叶片全长上的分布,由图8 分析得到在风速为7 m/s时摆振弯矩的波动最大,因此选择7 m/s 计算.

图9 为风速为7 m/s 时不同标准差下摆振弯矩在叶片全长上的分布.三种标准差下均值基本相同,标准差越大摆振弯矩波动越大.三种标准差下摆振弯矩均在r/R为0.6∼0.8 时波动最大,标准差为5%时最大波动幅度为13.32%,标准差为10%时最大波动幅度为25.16%,标准差为15%时最大波动幅度为35.18%.

图9 不同标准差下摆振弯矩在叶片全长上的分布Fig.9 Distribution of edgewise moment on the full length of the blade under different standard deviations

3.3 周向和轴向诱导因子

为进一步分析不确定性影响,计算轴向诱导因子和周向诱导因子在叶片全长上分布.参考文献[29]中给出了平均风速为6.7 m/s 时轴向诱导因子实际测量值,因此选择6.7 m/s 进行计算.

图10 为三种标准差下周向诱导因子不确定性在叶片全长分布对比.三种标准差下均值基本相同,在相同半径位置标准差越大,周向诱导因子波动越大,且越靠近叶根位置周向诱导因子波动越大.三种标准差下,周向诱导因子均在r/R为0.18 时最大,标准差为5%时最大波动幅度为13.23%,标准差为10%时最大波动幅度为24.38%,标准差为15%时最大波动幅度为35.78%.表明风轮叶片中部到叶尖位置流动较为稳定,受不确定性影响较小,而叶片根部靠近风轮中心受风速不确定性影响较大,可以在根部位置采取措施以改善不确定流动对风力机气动性能的影响.

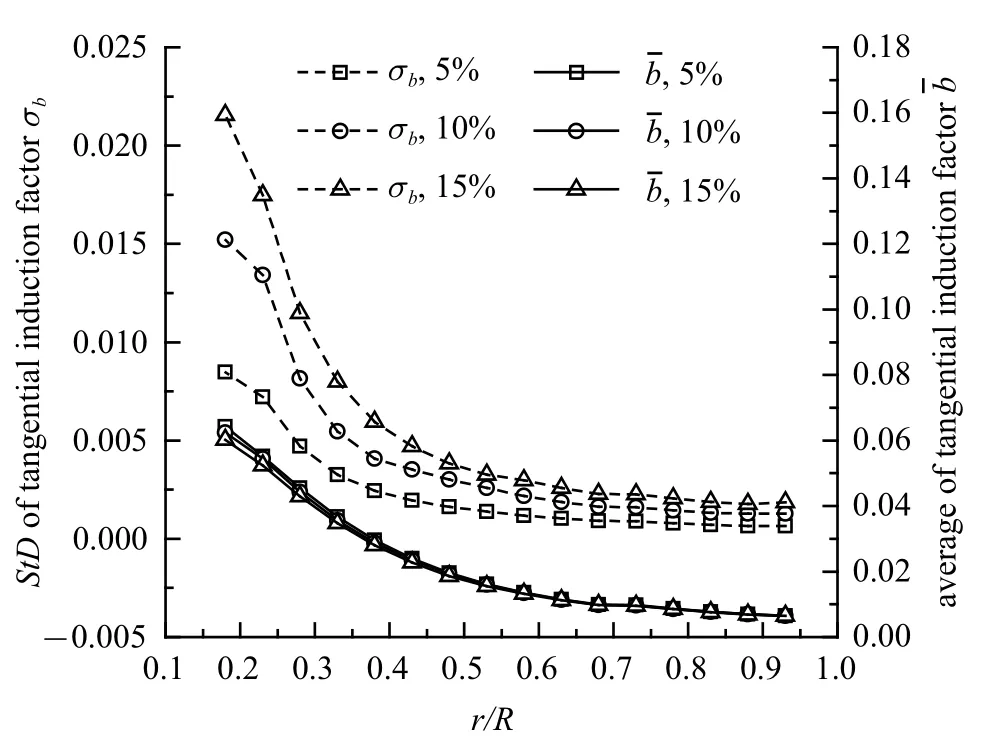
图10 不同标准差下周向诱导因子不确定性分布Fig.10 Uncertainty distribution of tangential induction factor under different standard deviations

图11 为平均风速为6.7 m/s 时,三种标准差下轴向诱导因子不确定性在叶片全长分布对比.在三种标准差下均值基本相同,相同半径位置,风速标准差越大轴向诱导因子波动越大.标准差为5%时,轴向诱导因子的波动在r/R为0.23 最大,最大波动幅度为4.71%;标准差为10%时,轴向诱导因子的波动在r/R为0.38 时最大,最大波动幅度为7.42%;标准差为15%时,轴向诱导因子波动在r/R为0.43 时最大,最大波动幅度为11.64%.