基于BP 神经网络与小冲杆试验确定在役管道钢弹塑性性能方法研究1)

宋明 李旭阳 曹宇光 甄莹 司伟山

(中国石油大学(华东)储运与建筑工程学院,青岛 266580)

引言

近些年来,长距离油气管道发展迅猛,输送压力不断提高.输油气管道长期在高温、高压、易腐蚀环境下工作,其材料易于发生劣化和损伤,极易导致安全事故的发生.因此对在役管道进行力学性能测试,评估和预测其结构完整性与剩余寿命变得尤为重要.常规力学性能评价方法如单轴拉伸试验、紧凑拉伸试验等[1],虽可直接得到材料弹性模量、屈服强度、抗拉强度与断裂韧性等材料参数,但试验所需试样尺寸较大,通常需要对管道进行破坏性取样,停输并截取管道不可避免.因此,为了获得在役管道材料力学性能,并尽可能降低损失与成本,微损试样试验测试方法得到迅速发展[2-5].

小冲杆试验(small punch test,SPT)[6-7]是一种近乎“无损”的微型试样试验方法,其试样尺寸为Φ10 mm×0.5 mm,通过试验可以得到试样中心点的载荷−位移曲线、断口相关数据等,其中包含了材料的弹塑性变形行为与断裂特征.在小冲杆试验发展历史上,Mao 等[8]分别将小冲杆试验屈服载荷、最大载荷与材料屈服强度、抗拉强度相关联,给出了相对应的经验公式.Chica 等[9]则对小冲杆试验载荷−位移曲线初始阶段进行分析,将初始阶段斜率与材料弹性模量相关联,得到两者之间的经验公式.Peng 等[10]基于等效能量原理,对小冲杆试验载荷−位移曲线第三阶段进行分析,得到了材料的真应力−应变曲线与抗拉强度.Baik 等[11]将载荷−位移曲线下的面积定义为小冲杆断裂能,并发现夏比V 型缺口试验结果与小冲杆试验结果之间的相关性,确定了材料韧脆转变温度.Hurst 等[10]提出了一种基于断裂能的环形缺口小冲杆试样J积分估算方法,并且采用标准小冲杆试验,对J-R抗弯曲线和断裂韧性JIC进行了局部分析模拟.众多学者基于自己的试验结果均采用经验关联的方式给出获取材料强度和断裂韧性的关联公式[12-19],然而由于试验所用材料、试验机结构、尺寸、加载方式,以及小冲杆试验载荷−位移曲线上屈服载荷定义方法[20]的差异,通过试验数据拟合得到的经验公式也不尽相同,彼此之间并能不通用,造成重复研究与研究资源的浪费.因此,亟待找到更合理和有效的方法关联小冲杆试验结果与常规试验结果.

本文提出了一种利用小冲杆试验[21-23]、有限元模拟与人工智能BP (back-propagation)神经网络[24-26]相结合,准确获得材料真应力−应变曲线,从而获得材料弹塑性力学性能的方法.通过经试验验证的含Gurson-Tvergaard-Needleman(GTN)损伤参数的小冲杆试验有限元模型得到457 组假想材料小冲杆试验载荷−位移曲线,结合其对应的真应力−应变曲线对BP 神经网络进行训练,在两者之间建立关联关系.将小冲杆试验得到的X80 管道钢载荷−位移曲线输入BP 神经网络,得到X80 管道钢的真应力−应变曲线,从而得到其屈服强度与抗拉强度,并用单轴拉伸试验结果验证该方法的有效性与准确性.为了进一步推广得到的关联关系之广泛适用性,利用训练好的BP 神经网络,对已有文献[10,27]中AISI 304L,P92,DP600 等材料的小冲杆试验数据进行处理,将结果与文献中单轴拉伸试验结果相对比,证明了相较于常规经验关联法,此方法获得材料力学性能具有准确性高、效率高、成本低等优点.

1 试验

1.1 单轴拉伸试验

试验所用X80 管道钢的化学元素C,Si,Mn,P,S,Cr,Mo,Ni,Nb,V,Ti,Cu 含量分别为0.043%,0.23%,1.87%,0.01%,0.0028%,0.025%,0.27%,0.23%,0.06%,0.006%,0.017%,0.13%.采用数字图像相关(digital image correlation,DIC)方法获得X80 管道钢的工程应力−应变曲线.DIC 测试装置如图1 所示,利用两台CCD(charge-coupled device)摄像机记录拉伸过程,通过VIC-3D 软件处理得到单轴拉伸试样在室温(Tr=23◦C)下的变形过程,共进行了三组试验,试样断裂时的应变分布和工程应力−应变曲线如图2(a)所示.由此得到X80 管道钢的弹性模量E=206 GPa,ReL=594 MPa,抗拉强度Rm=713 MPa.

图1 (a)DIC 装置(b)X80 管线钢拉伸试验散斑试样Fig.1 (a)The setup of digital image correlation(DIC)device,and(b)speckled specimen of X80 pipeline steel used in tensile test

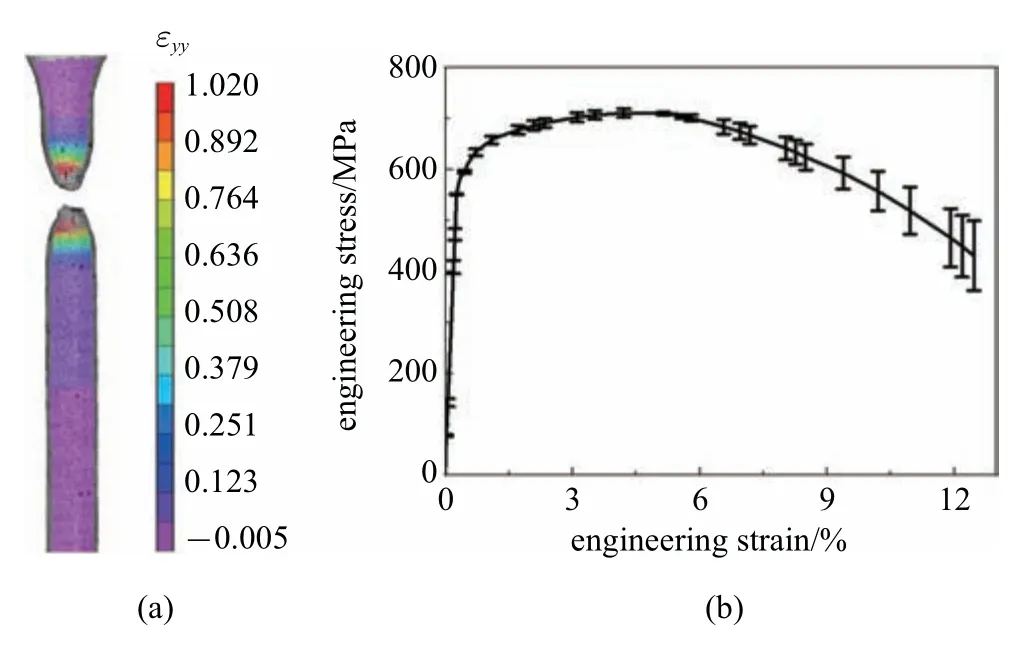
图2 (a)试样表面应变分布(b)X80 管道钢工程应力−应变曲线Fig.2 (a)Strain distribution on specimen surface and(b)engineering stress-strain curve of X80 pipeline steel

数值模拟所需X80 管道钢材料塑性参数由真应力−应变得到.Hollomon 公式可以用于描述大多数韧性材料的弹塑性本构关系[28]

式中,R为真应力,K为强度系数,ε 为真应变,n为应变硬化指数.材料真应力R与真应变ε 可分别通过式(2)、式(3)计算得到

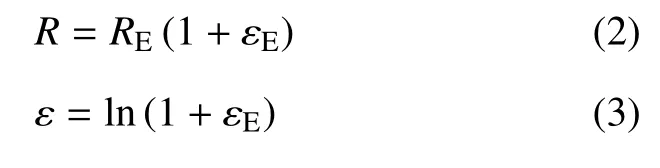
式中,RE为工程应力,εE为工程应变.得到如图3 所示的材料真应力−应变曲线后,将曲线处于屈服强度与抗拉强度之间的部分利用幂函数形式进行拟合,得到Hollomon 公式中的参数K与n.

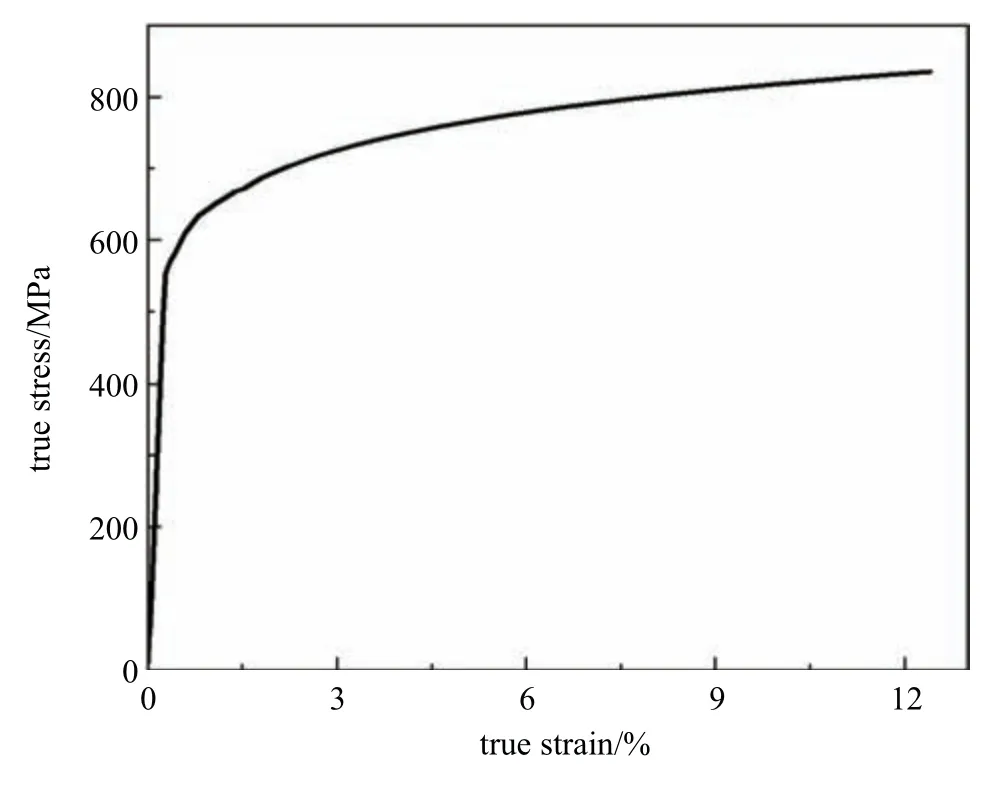
图3 X80 管道钢真应力−应变曲线Fig.3 True stress-strain curve of X80 pipeline steel

此外对上述公式进行推导可得到工程应力与真应力应变之间的关系,可表示为

式中,e=2.718,为自然常数.对于遵循Hollomon 本构关系的材料,当工程应力达到最大值,即Rm时,极限应变εE等于应变硬化指数n[29],因此抗拉强度可表示为[30]

由上述关系可知,不同材料的抗拉强度可由其对应的Hollomon 公式反推得到.

1.2 小冲杆试验

小冲杆装置如图4(a)所示,冲杆头部为半球形,半径r=1.25 mm,下夹具孔径D=4 mm,下夹具倒角半径R=0.2 mm,试样厚度t=0.500 mm,直径d=10 mm,试样放于下夹具凹槽中,并用上夹具压紧,防止其在试验过程中出现滑动.试验时冲杆向下施加载荷,速率恒定为0.2 mm/min,将试样中心下压直至试样发生断裂,记录整个试验过程试样所受载荷与冲头位移,从而得到小冲杆试验载荷−位移曲线,如图4(b)所示.整条曲线可分为5 部分:I.弹性弯曲变形阶段;II.弹塑性弯曲阶段;III.塑性强化阶段;IV.基于材料损伤的软化阶段;V.裂纹生成直至试样断裂阶段[31-32].通过小冲杆试验载荷−位移曲线可得到表征材料弹塑性行为的相关参数,包括曲线第一阶段弹性段的初始斜率slopeini,通过最小二乘法拟合第一、第二阶段得到的屈服载荷FP以及曲线最高点对应的最大载荷Fmax,如图4(b)所示.

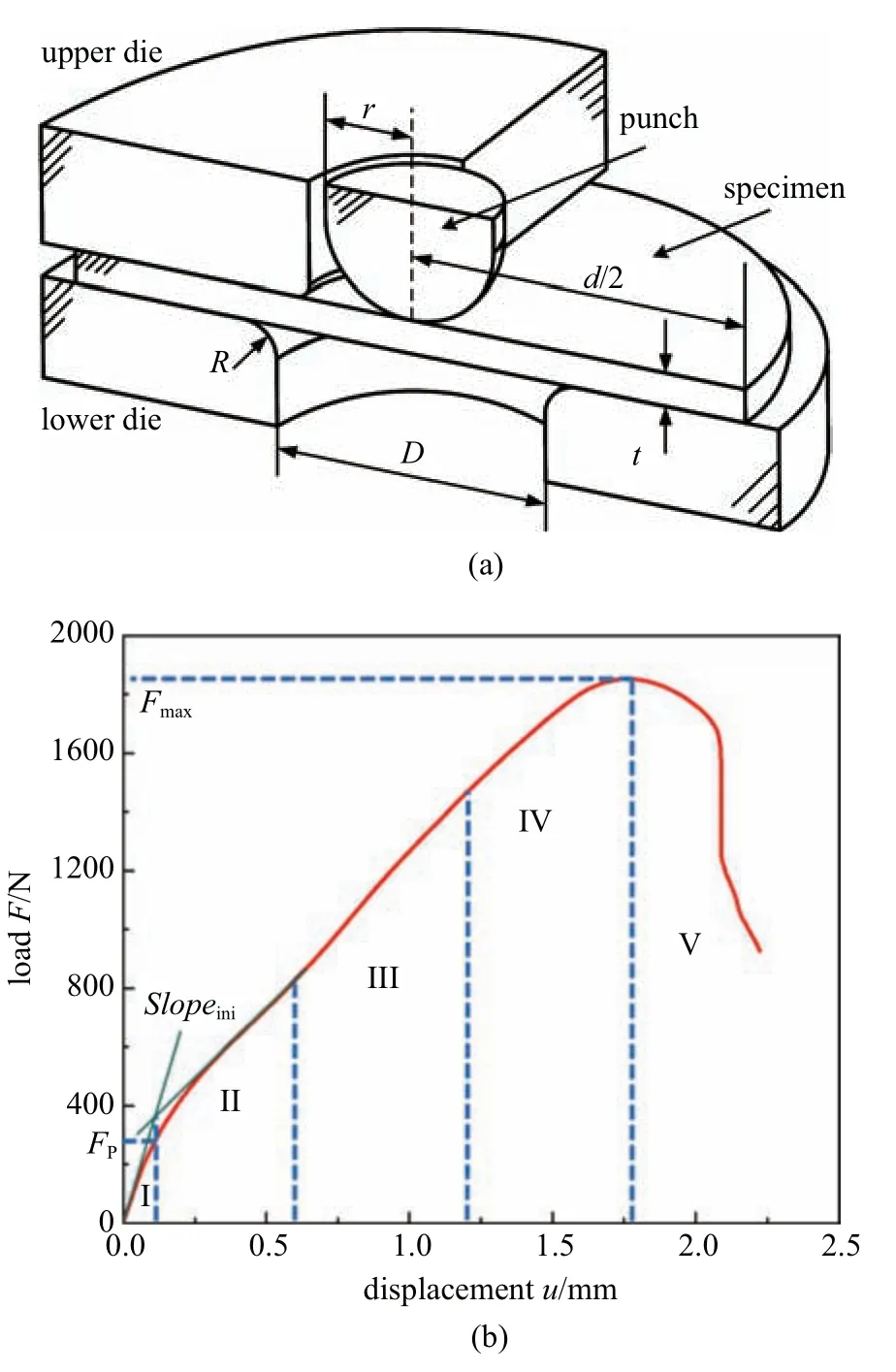
图4 (a)小冲杆试验装置示意图和(b)小冲杆试验载荷−位移曲线Fig.4 (a)Schematic of the SPT device,and(b)load-displacement curve of SPT

这些参数与通过单轴拉伸试验得到的材料弹性模量E、屈服强度ReL与抗拉强度Rm之间有着紧密的联系[20].一些学者[8,33-34]对多种材料进行小冲杆试验与单轴拉伸试验,并将试验结果进行经验关联,得到获取材料力学性能参数的经验公式如下

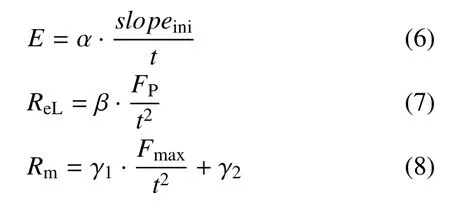
式中,t为小冲杆试样初始厚度;α,β,γ1,γ2为材料相关系数,分别等于17.47,0.36,0.13,−0.32.这些系数通过对不同材料试验结果进行回归分析而得到.将从X80 管道钢小冲杆试验结果获得的参数代入式(6)∼式(8),分别得到弹性模量E=225 GPa,屈服强度ReL=473 MPa,抗拉强度Rm=983 MPa,与单轴拉伸试验结果相比,误差分别为:9.2%,20.3%,37.8%.由此可发现,直接利用其他学者得到的经验公式获取X80管道钢材料力学性能参数,与标准常规试验相比误差较大.若要利用小冲杆试验较为准确地获取管道钢材料弹性模量、屈服强度、抗拉强度等力学性能参数,需对多种管道钢材料分别进行小冲杆试验与单轴拉伸试验,拟合新的适用于管道钢的经验公式.这样势必会进行重复研究,不得不切取在役管道,耗费大量的研究资源与成本,并且总结的经验公式可能仅适用于管道钢材料.基于以上原因,亟待开发新的试验方法在保证管道完整性的情况下获取在役管道材料力学性能参数.因此本研究采用人工智能BP 神经网络结合小冲杆试验与数值模拟获取在役管道材料弹塑性力学性能参数.

2 BP 神经网络

BP 神经网络可对大量数据进行训练,在两种不同因素之间建立合理、紧密的关联关系.本文将小冲杆试验载荷−位移曲线作为输入集,真应力−应变曲线作为输出集,所采用的BP 神经网络主要训练方案如图5 所示.

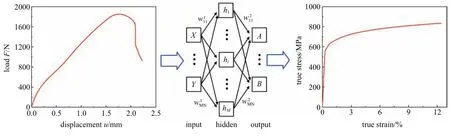
图5 BP 神经网络训练方案Fig.5 Training scheme of BP neural network

图6 BP 神经网络计算原理Fig.6 Computational principle of BP neural network

BP 神经网络训练过程中,需对输入数据进行计算,不断减小误差,如图6 所示.计算过程主要分为两部分:(1)首先设定目标误差值,输入一组同种材料的小冲杆载荷−位移数据与真应力−应变数据,第一层神经元接收小冲杆试验载荷−位移数据后,通过本层对应的激活函数f1(e)对其进行计算,将计算结果y1输出到第二层神经元.输出集y由第二层神经元计算得到,求出其与输入真应力−应变数据之间的误差δ;(2)将计算得到的误差δ 反馈回前两层神经元,通过式(9)∼式(11)分别对每层神经元的权值进行修正,并利用修正后的权值重复进行第(1)步运算,直至误差小于预设的目标误差值

式中,w1,w2,w3为第一次训练连接权值,为修正后的第二次训练权值,η 为学习率,f(e)为激活函数,δ 为计算误差.

3 小冲杆试验有限元模拟与假想材料力学性能获取

本研究采用有限元软件ABAQUS 对小冲杆试验进行有限元模拟并获取大量假想材料的力学性能.小冲杆试样为圆片状轴对称结构,因此可直接简化为二维轴对称模型,不考虑冲头、上夹具、下夹具的变形将其设为刚体,上夹具与下夹具为固定约束,控制冲头向下位移来对试件施加载荷.建立试件与冲头、上夹具、下夹具之间的接触,摩擦系数µ=0.15.单元选择4 节点二次缩减积分单元CAX4R,厚度方向共划分10 层网格,如图7 所示.

图7 小冲杆试验轴对称有限元模型Fig.7 Axisymmetric finite element model of small punch test

3.1 材料参数

为了模拟小冲杆试验过程中试样的弹塑性变形、损伤与断裂行为,有限元模型中导入了GTN 连续损伤模型.材料参数的定义分为两部分:(1)材料弹塑性参数定义;(2)材料损伤参数定义.有限元模型中所需材料弹塑性参数包括弹性模量、泊松比与应力应变关系,而这些参数可通过单轴拉伸试验得到.

GTN 损伤模型的屈服函数可以表示为

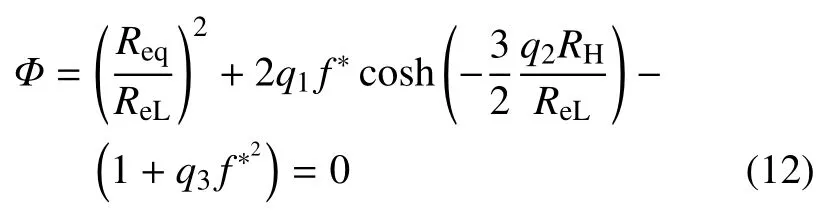
式中,Req为宏观Mises 等效应力,ReL为基体材料的屈服强度,RH为宏观静水应力,q1,q2,q3为损伤参数.通过数值计算分析,Tvergaard[35]及文献[36]中给出的损伤参数常用取值为q1=1.5,q2=l,为孔洞的体积分数,当f∗取零值时,上式退化为von Mises 屈服函数.f∗的定义为

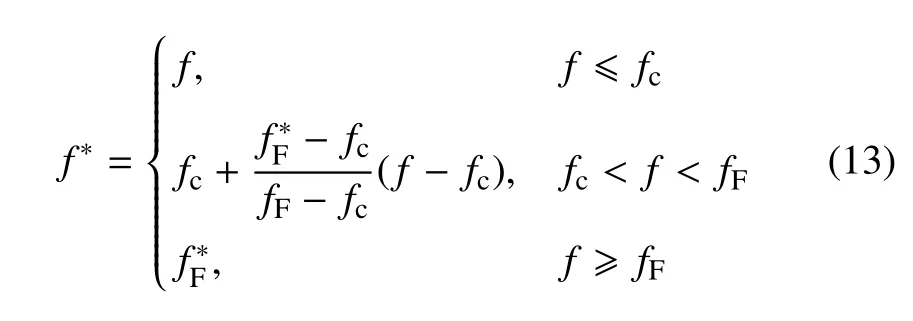
式中,fc为孔洞开始发生聚合时的临界孔洞体积分数,fF为材料失效时的孔洞体积分数,即应力承载能力为零时的极限孔洞体积分数,GTN 模型中的孔洞体积分数包括两部分:(1)现有孔洞逐渐增长,导致体积分数增大;(2)由于较大的塑性应变,材料中产生新的孔洞.因此,如果考虑应变控制成核,孔洞体积分数的增大可写为

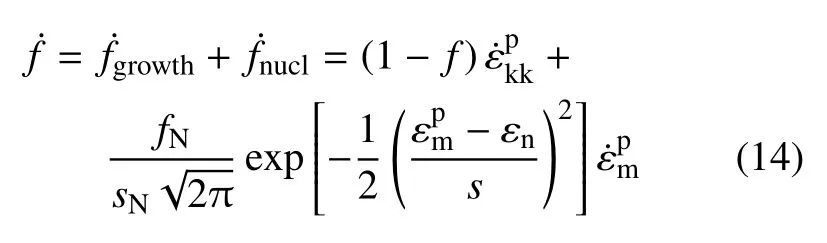
在小冲杆试验有限元模型中,X80 管道钢材料的孔洞参数f0,fN,fc,fF未知,因此需确定这些参数的取值.由于材料的微观损伤难以观测与测量[37],因此大多数学者通过多次调参试算,将模拟得到的载荷−位移曲线与试验结果对比,最佳匹配时所用参数作为此种材料的GTN 损伤参数.本文也使用此种方法确定材料损伤参数,具体做法如下所述.通过线切割从管道上切取直径10.0 mm、厚度0.600 mm 的试片.使用砂纸对切取的试片进行打磨,去除试样表面过热和加工硬化影响区,使试样中不含有任何裂纹和其他宏观缺陷.为保证试验的准确性,准备三组试验,最终试样厚度t分别为0.495 mm,0.498 mm 和0.499 mm,分别对其进行试验,记录每个试样在整个试验过程中的载荷−位移数据,得到三组小冲杆载荷−位移曲线.对多组小冲杆试验有限元模型进行模拟,保证其塑性参数不变,只改变其GTN 损伤参数,将多个模拟结果与试验结果对比,找到与试验结果匹配度最高的曲线,如图8 所示.将此模型采用的GTN损伤参数作为X80 管道钢材料的GTN 损伤参数.最终确定的GTN 损伤参数为:q1,q2,q3,εN,SN,f0,fN,fc,fF分别为1.5,1,2.25,0.3,0.1,0.002 5,0.000 8,0.03,0.15.

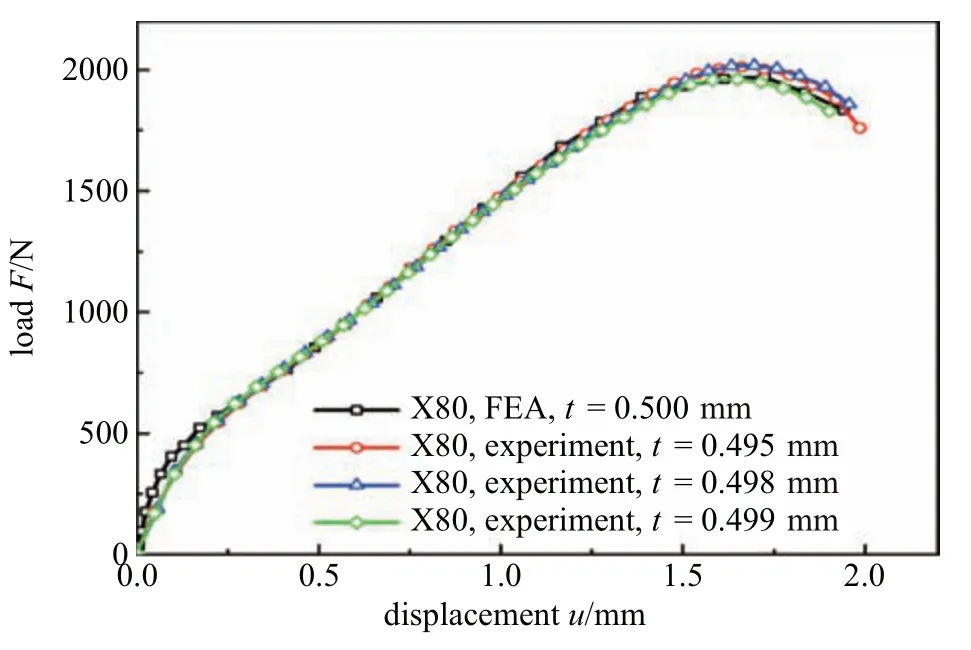
图8 小冲杆试验结果与有限元模拟结果对比Fig.8 Comparisons between experimental and simulation results of small punch test

4 神经网络识别程序

4.1 数据库构建

采用上一节经过验证的有限元模型,通过改变Hollomon 公式中的K,n参数,经过计算,得到457 种假想材料的真应力−应变曲线和小冲杆载荷−位移曲线.将这些数据作为训练神经网络的数据库.BP神经网络训练集包括两部分:小冲杆载荷−位移曲线作为输入集,同种材料真应力−应变曲线作为输出集.其中真应力−应变曲线可以通过系统地改变Hollomon 公式中的参数K与n得到.若要得到较为准确的训练结果,需保证训练集数据的准确性与全面性,因此数据库应包含大部分常见金属材料真应力−应变曲线.大多数金属材料的应变硬化指数n取值范围为[0.005,0.6],强度系数K的取值范围为[200,2000][38].但由于K值较小时,随着n值的减小,真应变为0.002 时对应的真应力即材料屈服强度变得极小,此时材料屈强比变得极小,而此类金属极为少见,因此为提高神经网络训练的结果,不考虑这类真应力−应变曲线.最终确定的K与n参数取值范围如表1 所示.

每改变一次参数K与n便可得到一条新的真应力−应变曲线,将得到的每条真应力−应变曲线依次代入小冲杆试验有限元模型,进行计算得到完整的载荷−位移曲线.取小冲杆载荷−位移曲线下降段最终载荷大小为最大载荷的80%,部分数据如图9 所示.建立数据库的过程中并未考虑材料GTN 参数的变化,因为根据已有文献,不同管道钢微观组织与缺陷的分布基本一致,故本研究中假设有限元模型中所有假想材料的GTN 参数一致.

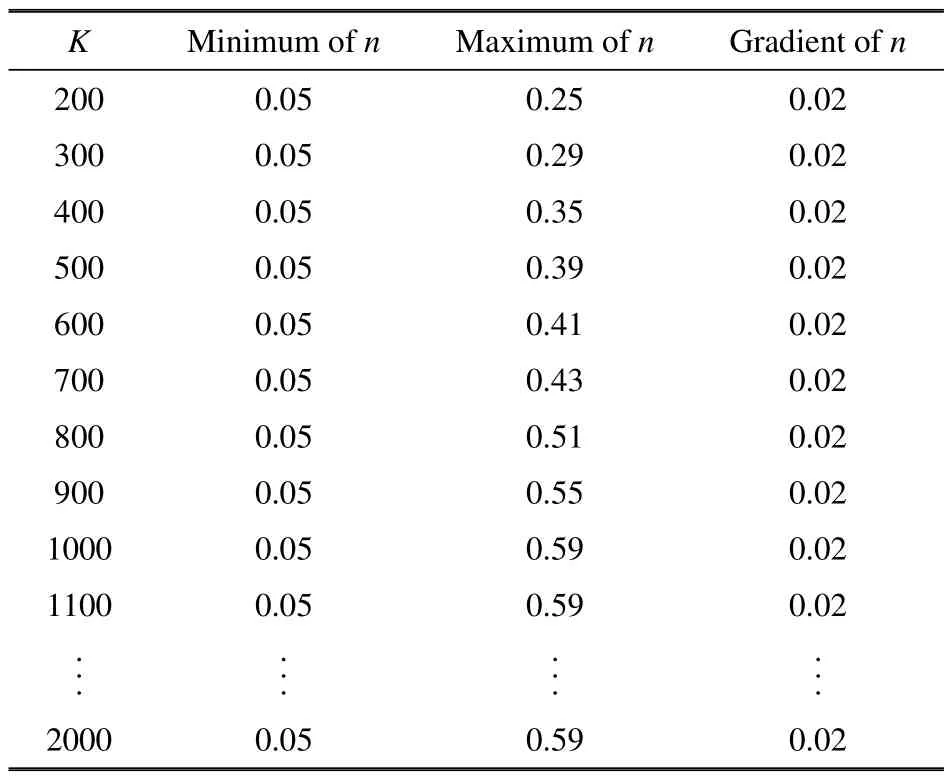
表1 K 与n 取值范围Table 1 Range of parameter K and n

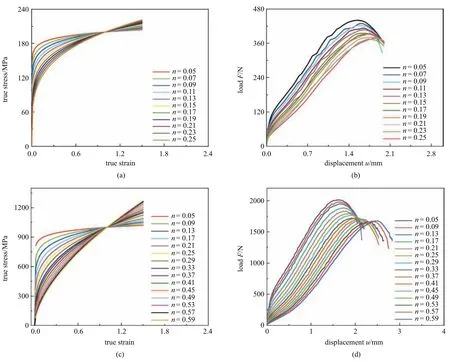
图9 BP 神经网络训练集数据,不同参数n 对应的真应力−应变曲线:(a)K=200,(c)K=1000,(e)K=2000 和不同参数n 对应的小冲杆试验载荷−位移曲线(b)K=200,(d)K=1000,(f)K=2000Fig.9 BP neural network training set data:the true stress-strain curves corresponding to different parameters n(a)K=200,(c)K=1000,(e)K=2000,and the load-displacement curves of SPT corresponding to different parameters n(b)K=200,(d)K=1000,(f)K=2000

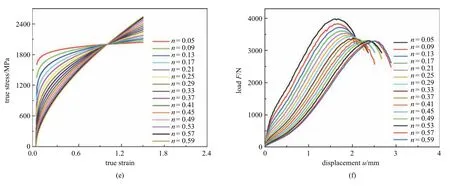
图9 BP 神经网络训练集数据,不同参数n 对应的真应力−应变曲线:(a)K=200,(c)K=1000,(e)K=2000 和不同参数n 对应的小冲杆试验载荷−位移曲线(b)K=200,(d)K=1000,(f)K=2000(续)Fig.9 BP neural network training set data:the true stress-strain curves corresponding to different parameters n(a)K=200,(c)K=1000,(e)K=2000,and the load-displacement curves of SPT corresponding to different parameters n(b)K=200,(d)K=1000,(f)K=2000(continued)

表2 BP 神经网络训练集数据库结构Table 2 Database structure of training set of BP neural network

在训练BP 神经网络时,输入、输出数据只能分别为一个列矩阵.小冲杆试验获得的材料载荷−位移曲线与真应力−应变曲线为独立的两组数据,每组数据分别包含横坐标(试样中心点位移与真应变)与纵坐标(载荷与真应力).因此需要将每组数据包含的横坐标与纵坐标转化为一个列矩阵.具体转化方式如表2 所示.其中,小冲杆试验载荷−位移曲线用(Xi,j,Yi,j)来表示,真应力−应变曲线用(Am,n,Bm,n)来表示,每条载荷−位移曲线取120 组坐标,真应力−应变曲线取50 组坐标,下标i,m为输入数据点序号,j,n为输入训练集序号.由此,可以把(X1,Y1),(X2,Y2),···,(X120,Y120)形式排列的小冲杆试验载荷−位移曲线坐标转化为[X1,X2,···,X120,Y1,Y2,···,Y120]形式的列矩阵,材料真应力−应变曲线转化方式与小冲杆试验载荷−位移曲线转化方式相同.全部457 组假想材料的BP 神经网络训练集数据库结构如表2 所示.

4.2 BP 神经网络计算结果

将转化完成的训练集数据输入BP 神经网络进行训练,当误差小于预设误差1.0×10−5时,训练完成.将小冲杆试验得到的X80 管道钢载荷−位移曲线输入训练好的BP 神经网络便得到相应的真应力−应变曲线.该结果与单轴拉伸试验结果进行对比,如图10 所示.通过对比发现,BP 神经网络计算的结果与单轴拉伸试验所得材料真应力−应变曲线误差最大为3.7%,最小为2.5%.

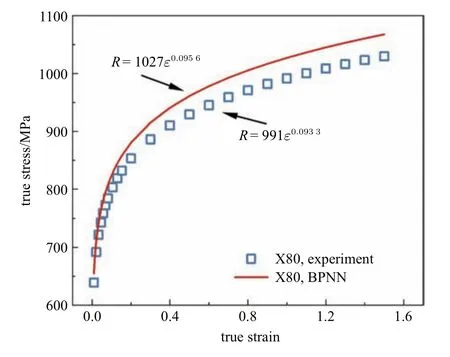
图10 BP 神经网络与单轴拉伸试验得到的X80 管道钢真应力−应变曲线对比Fig.10 Comparison of true stress-strain curves of X80 pipeline steel obtained between BP neural network and uniaxial tensile tests

为了进一步验证此BP 神经网络计算结果的准确性与广泛适用性,分别引用文献[10]与文献[27]中3 种实验材料AISI 304L,P92,DP600 的小冲杆载荷−位移曲线与单轴拉伸试验结果,进行对比.将3种材料的载荷−位移曲线数据分别代入训练好的BP神经网络,经过计算,得到相对应的真应力−应变曲线.将计算结果与文献[10]、文献[27]中单轴拉伸试验的结果进行对比,如图11 所示.

对试验与BP 神经网络计算得到的真应力−应变曲线数据进行处理,拟合曲线得到其对应Hollomon公式中的参数K与n,通过式(5)计算得到其抗拉强度.经过计算,发现多种材料的真应力−应变曲线在应变为0.002 时与工程应力−应变曲线中残余塑性应变为0.002 时的应力值误差在10%以内[10,27,39-41],故本文采用真应变为0.002 时对应的应力值,作为材料的屈服强度.单轴拉伸试验结果与通过BP 神经网络计算得到的结果列于表3 中.

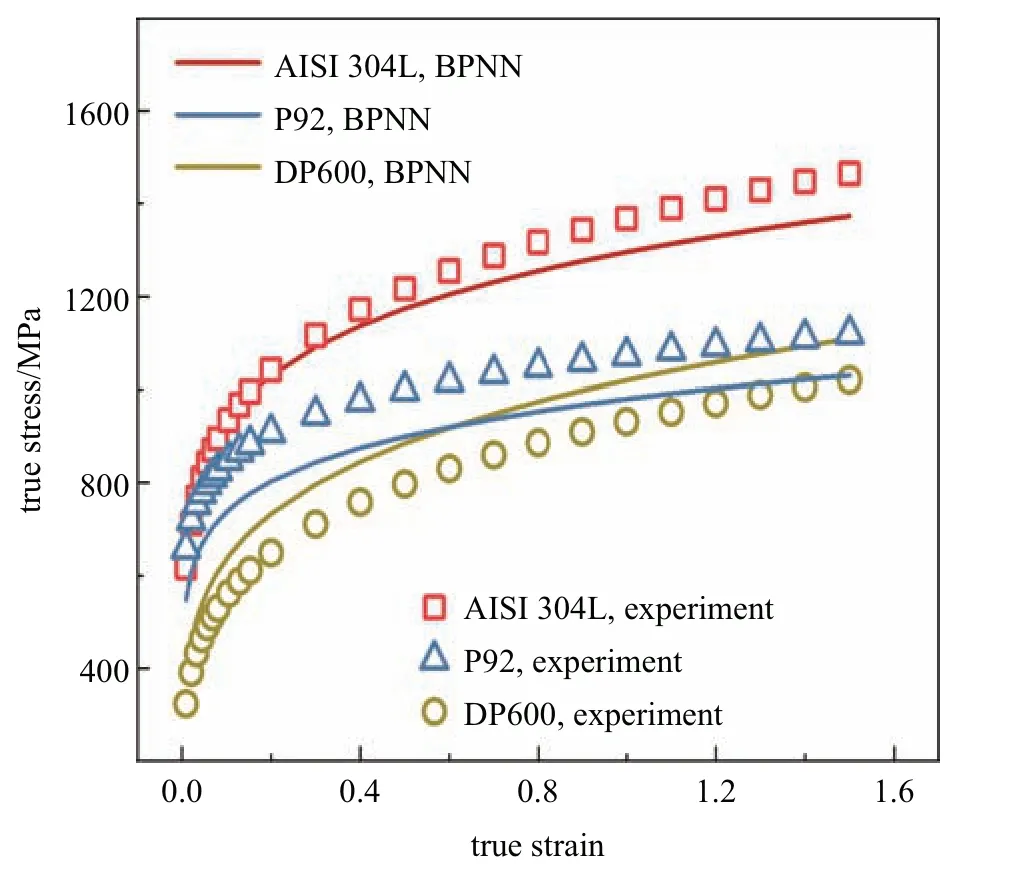
图11 BP 神经网络与单轴拉伸试验得到的文献中材料的真应力−应变曲线对比Fig.11 Comparison of true stress-strain curves of materials in reference obtained between BP neural network and uniaxial tensile tests

表3 BP 神经网络得到的材料力学性能参数Table 3 Mechanical properties of materials obtained by BP neural network

从上表数据可以看出,由BP 神经网络计算得到X80 管道钢材料与其他常见金属材料的弹塑性力学性能参数与单轴拉伸试验结果相比,最大误差为9.3%,远小于利用常规经验关联法计算结果的误差37.8%.并且,也说明本文提出的BP 神经网络关联方法不仅适用于管道钢材料,也适用于其他常见金属材料.只需将小冲杆试验得到材料的载荷−位移曲线输入训练好的BP 神经网络,经过计算,便可获得材料真应力−应变曲线,进而得到相应材料的弹塑性力学性能参数.

5 结论

本研究提出了一种利用小冲杆试验、有限元模拟与BP 神经网络相结合,准确获得材料真应力−应变曲线,从而获得材料完整弹塑性力学性能的方法.通过由试验验证的含GTN 损伤参数的小冲杆试验有限元模型得到457 组小冲杆试验载荷−位移曲线,结合其相对应的真应力−应变曲线对BP 神经网络进行训练,在两者之间建立关联关系.通过对比X80 管道钢小冲杆试验与单轴拉伸试验结果以及现有文献中不同材料的试验数据,验证该方法的准确性与广泛适用性,得到以下结论:

(1)含有GTN 损伤参数的小冲杆试验有限元模型得到的载荷−位移曲线与试验结果具有很高的吻合度,可代替试验获取BP 神经网络训练集数据.

(2)将X80 管道钢小冲杆试验载荷−位移曲线代入BP 神经网络计算得到其真应力−应变曲线,进而得到屈服强度=567 MPa,抗拉强度=746 MPa,与单轴拉伸试验结果相比误差分别为−6.6%与4.6%,证明BP 神经网络结合小冲杆试验可以较准确地得到管道钢材料弹塑性力学性能.

(3)利用BP 神经网络对文献中已有材料试验数据进行计算,对比文献中单轴拉伸试验结果,最大误差为9.3%,低于常规经验关联法误差.表明本文提出的方法广泛适用于在役管道钢以及多种金属材料真应力−应变曲线的获取.