随机和区间非齐次线性哈密顿系统的比较研究及其应用1)

邱志平 姜 南

(北京航空航天大学航空科学与工程学院,北京 100191)

引言

随着计算机技术的飞速发展,研究人员越来越追求更高效、更稳定和长时间模拟能力更强的数值算法[1].同一力学问题有牛顿力学、拉格朗日力学、哈密顿力学体系三种表示形式,其中一切可忽略耗散的物理过程都可以表示为某种哈密顿形式,但由于求解途径不同,产生的计算结果可能是不等效的[2].传统算法除少数例外,都不是辛算法,不可避免地带有人为耗散性等歪曲体系特征的缺陷,用于短期模拟尚可,用于长期跟踪则会导致结果严重失真[3-4].而哈密顿系统辛算法却有保持体系结构的优点,在结构对称性和守恒性方面优于传统算法,特别在稳定性和长期跟踪能力上具有独特优越性[2-5].

哈密顿系统辛算法的思想始于20 世纪80 年代Ruth[6]和冯康[7]的工作.1983 年,Ruth[6]构造了可分哈密顿系统的前三阶辛差分格式.1984 年,冯康[7]首次系统地提出了哈密顿系统的辛算法,开创了哈密顿力学数值计算的新领域.1988 年,Sanz-Serna[8]、Lasagni[9]和Suris[10]分别从不同角度给出了辛Runge-Kutta 方法的判定条件.1993 年,Sun[11]对一般的哈密顿系统构造了辛分块Runge-Kutta 方法.2000 年前后,Bridges[12]、Reich[13]和Marsden等[14]构建了多辛算法的理论框架.之后,变分积分子、离散梯度法、投影算法、分裂组合算法、对称算法等[15]一系列方法不断提出并发展.近年来,无网格格式[16]、连续级Runge-Kutta 方法[17]等辛算法也相继被提出.深入的理论分析和大量的数值实验令人信服地表明,辛算法在数值计算中具有显著优越性.

然而,动力系统中不可避免地存在大量的、不同程度的不确定性[18].例如,工程结构中的典型不确定性有:建模过程中的简化操作导致所建模型存在误差,制造环境、材料多相特征等因素使弹性模量、泊松比等材料参数具有分散性,制造及安装误差使结构几何尺寸具有不确定性,测量条件、外部环境等因素使外载荷具有不确定性等[19-20].这些不确定性将引起动力响应变化,响应不确定量有时甚至能达到参数不确定量的数倍[21].此外,不确定性的存在还会使系统的性质发生改变,保守系统若存在不确定性则不再保守.根据产生机理不同,不确定性可分为随机不确定性和认知不确定性[22-23]:随机不确定性是由自然变异和随机性而导致的不确定性,以随机模型定量化;认知不确定性是指受知识水平和社会环境等因素制约而产生的认知上的不确定性,通常以区间模型定量化.因此,需要在哈密顿系统中考虑随机和区间不确定性的影响,以确保动力学分析计算的合理有效性.

1984 年,Zambrini 首先基于变分原理提出了Nelson 随机力学在哈密顿力学下的运动方程,逐步建立了哈密顿力学下的随机力学体系.2002 年,Milstein 等[24]对一般的随机哈密顿系统构造了几类辛Runge-Kutta 方法,开创了随机哈密顿系统辛算法这一全新的研究领域.2007 年,王丽瑾[25]提出了随机变分积分子理论,使利用随机生成函数构造随机辛算法成为可能.2009 年,Bou-Rabee 和Owhadi[26]对随机哈密顿系统构造了随机变分积分子.近几年,丁效华课题组[27-28]也对随机哈密顿系统进行了研究,并构造了随机辛Runge-Kutta、辛分块Runge-Kutta 方法等.此外,朱位秋[29-30]研究了多自由度非线性随机动力学系统,在国际上首次提出了随机激励的耗散的哈密顿系统理论,构建了非线性随机动力学与控制的哈密顿理论框架.上述随机哈密顿系统相关研究主要聚焦随机白噪声激励,但没有考虑系统本身的参数随机性,并且考虑区间不确定性的哈密顿系统也未见有人研究.

哈密顿系统辛算法的工程结构应用方面,罗恩等[31]建立了多自由度系统弹性动力学的相空间非传统哈密顿变分原理,提出了称之为辛时间子域法的辛算法,精度和效率都具有明显优越性.邢誉峰课题组[32-33]针对结构动力学方程构造了多种辛差分格式,得到了令人满意的结果.高强等[34]用辛算法求解拉压刚度不同桁架的非线性动力问题,Li 等[35]构造了一类动力学初值问题的辛算法并应用于简谐振子和简支梁,Yang 等[36]用辛算法对超长细杆进行动力学数值模拟.也有学者对多辛算法的工程结构应用开展了相关研究,如梁[37]、板[38]、杆[39]的动力响应等.然而,用哈密顿系统求解含不确定性的结构动力响应还少有人研究.

本文针对随机和区间不确定性,对含参数不确定性的非齐次线性哈密顿系统的动力响应分析进行首次尝试,提出两种不确定性哈密顿系统的参数摄动法,突破传统哈密顿系统只适用于保守系统的局限性,并开展两种哈密顿系统不确定性响应的相容性研究,以期为结构动力响应评估提供更加有效稳定的数值计算方法.

1 确定性非齐次线性哈密顿系统

考虑哈密顿正则方程

其中,In是n阶单位矩阵;J是标准单位辛矩阵,满足J−1=JT=−J;H称为该系统的哈密顿函数.

哈密顿系统(1)称为线性的,如果哈密顿函数H是z的二次型

其中C为对称矩阵,即CT=C,于是正则方程(1)能够表示为

其中B=J−1C是无穷小辛阵,即满足JB+BTJ=0.

非齐次线性哈密顿系统是在线性哈密顿系统基础上增加了非齐次项

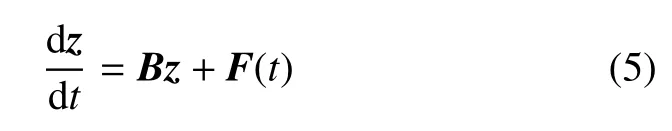
其中F(t)是与时间t有关的向量.

此时,哈密顿函数H′可以表示为

从而,非齐次线性哈密顿系统(5)可以表示为哈密顿正则方程(1)的形式.

对于哈密顿系统,其相空间配备着一个标准辛结构,也就是一个闭的微分2 形式

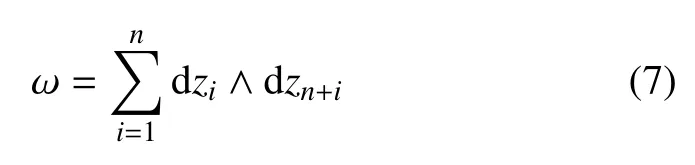
哈密顿系统相流保持相空间的辛结构不变,即

2 含扰动非齐次线性哈密顿系统的参数摄动法

假设非齐次线性哈密顿系统(5)中的矩阵B和向量F(t)中元素与系统参数b=(b1,b2,···,bm)T有关,此时,哈密顿系统(5)可以写为

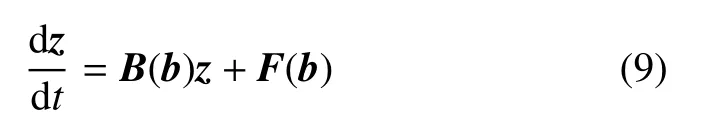
当系统参数b=(b1,b2,···,bm)T存在扰动时,矩阵B(b)和向量F(b)由标称值变化到扰动系统,分析扰动对哈密顿系统响应z的影响.

根据摄动理论,引入小参数ε、参数b、矩阵B、向量F和哈密顿系统的解z可以分别写为摄动级数展开形式

其中,ε 是小于单位1 的小量,b0,B0,F0和z0分别是b,B,F和z的标称值,bi,Bi,Fi和zi(i=1,2,···,p)分别是其第i阶摄动量.含ε 的项表示其与标称值相比是一个很小的量,在这种情况下,哈密顿系统的解z只有小变化.通过选择使|ε| 足够小的参数可以使级数收敛.

将式(10)代入式(9),得

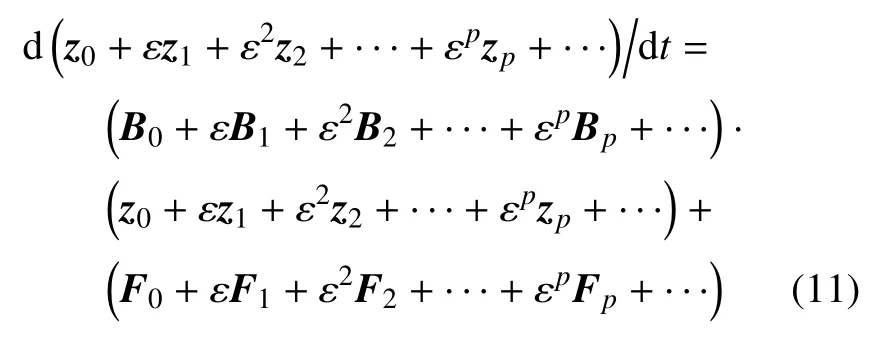
将式(11)展开,比较ε 的同次幂系数,可得

运用辛算法求解式(12)中第1 式可以得到z的标称部分,即z0.本文中采用的辛算法均为欧拉中点格式.对式(12)中其他式子的Bi和Fi(i=1,2,···,p),可以通过Taylor 展开获得,即将B和F在b=b0处分别进行Taylor 展开,得到

其中bij(i=1,2,···,p;j=1,2,···,m)是bi的分量.

由式(10)和式(13),可知

将式(12)中第1 式求得的z0和式(14)求得的B1,F1代入式(12)中第2 式并利用辛算法求解,可以求得z的第1 阶摄动量z1;进而可以通过依次求解式(12)中其他式子得到zi(i=2,3,···,p)的值.从而,z就可以按式(10)求得.在每一步都采用辛算法求解保证计算结果能够保持体系结构特征,避免传统算法带有的人为耗散性等歪曲体系特征的缺陷.在实际计算中,为了方便求解,常常展开到第1 阶摄动.

当参数b存在的扰动为随机或区间不确定性时,上述参数摄动法可以推广至求解随机或区间非齐次线性哈密顿系统,详细求解过程如下面第3、4 节所述.

3 随机非齐次线性哈密顿系统的参数摄动法

当系统参数b=(b1,b2,···,bm)T是随机变量时,矩阵B、向量F和哈密顿系统的解z也是随机的,它们可以分别看作围绕确定性部分(均值)有一个随机小扰动.因此,基于前述摄动理论,同样引入小参数ε,将b,B,F和z分别表示为

其中,bd,Bd,Fd和zd分别是b,B,F和z的确定性部分;bs,Bs,Fs和zs分别是其随机部分,且它们的均值均为0.

将式(15)代入式(9),得

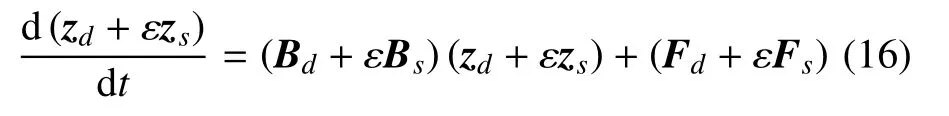
将式(16)展开,忽略O(ε2)高阶项,并比较ε 的同次幂系数,可得

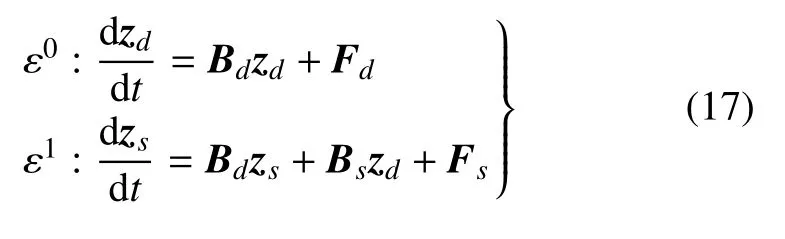
利用辛算法求解式(17)中第1 式可以求得z的确定性部分zd,即为z的均值.但无法由式(17)直接确定z的随机部分zs,需要进行变换后加以求解.

对式(15)求取数学期望,有

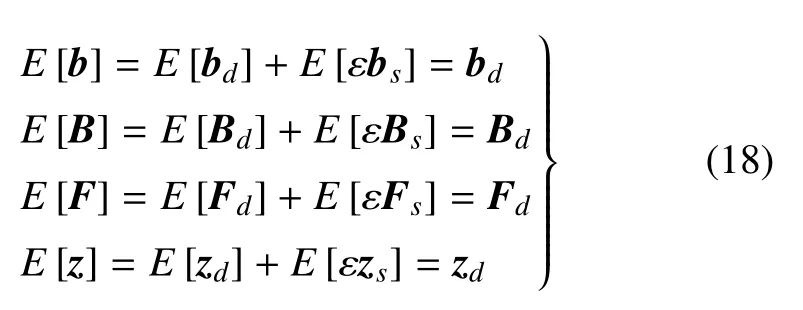
由于zd是一个确定性的向量,所以zd与z,zd与zs均相互独立,从而可得

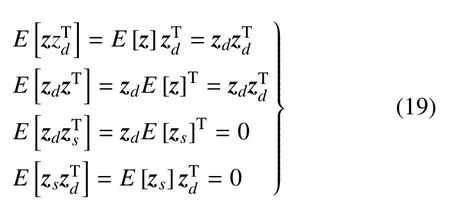
因此,z的协方差矩阵可以写为

式(20)中的E[zzT]可以写为

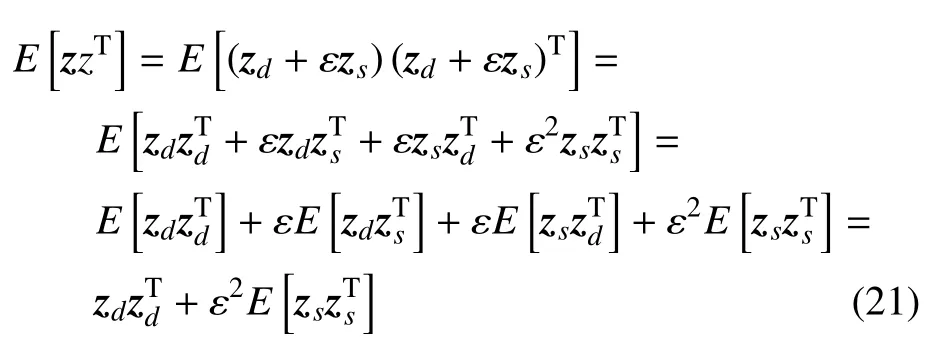
将式(21)代入式(20),可得协方差矩阵为

该协方差矩阵的对角元素表示各点的方差,其他非对角元素表示各点间的协方差.因此,z的各分量zi(i=1,2,···,2n)的方差为

同理,b的各分量bj(j=1,2,···,m)的方差为

将z在z=zd处进行一阶Taylor 展开得到

其中,bsj(j=1,2,···,m)是bs的分量.

从而,z的随机部分zs可以表示为

同理,Bs和Fs可以表示为

将式(26)∼式(27)代入式(17)中第2 式,得

其中Cov(bk,bl)表示bk和bl的协方差.

若参数bj是相互独立的,Cov(bk,bl)为0,则式(29)可以简化为

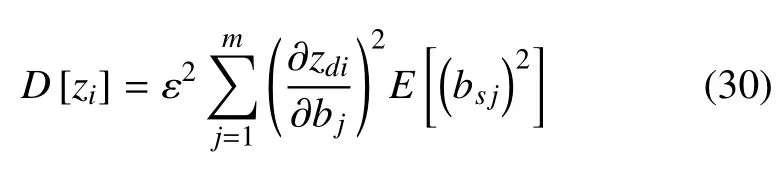
将式(24)代入式(30),就可以得到z的各分量zi(i=1,2,···,2n)的方差

因此,zi(i=1,2,···,2n)的标准差为

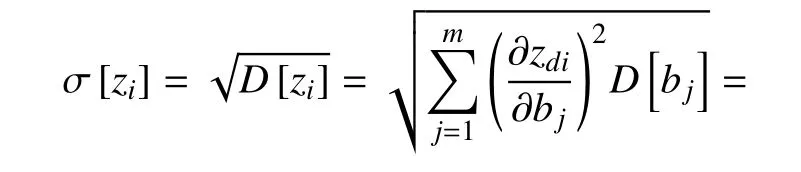
其中σ[bj]是bj(j=1,2,···,m)的标准差.

在计算求解过程中,求解式(17)中第1 式求得z的均值zd和求解式(28)求得z的随机部分zs都采用了辛算法,确保计算结果能够保持体系结构特征.

令k为正整数,则对zi(i=1,2,···,2n)而言,距其均值的距离为k倍标准差的范围为

其中范围的上界和下界分别为

4 区间非齐次线性哈密顿系统的参数摄动法

当系统参数b=(b1,b2,···,bm)T是区间变量时,即参数b在一个区间向量内取值,矩阵B、向量F和哈密顿系统的解z也分别在一个区间范围内取值

其中,bI,FI和zI是区间向量,BI是区间矩阵,分别是分别是其上界.

此时,哈密顿方程(9)可写为

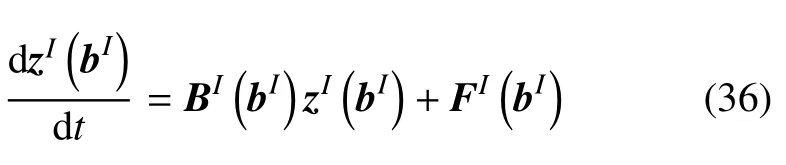
式(36)是区间非齐次线性哈密顿方程.

bI,BI,FI和zI的中值和半径分别为

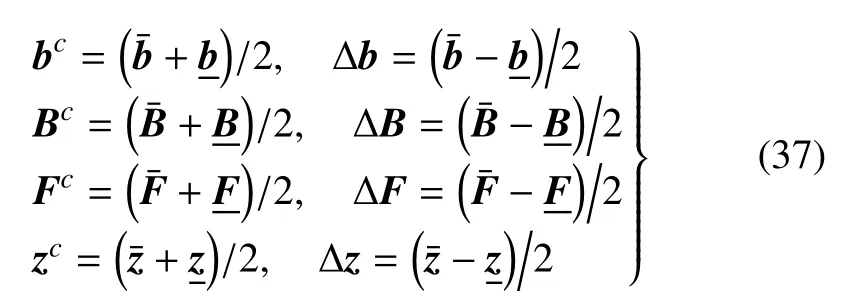
利用区间中心表示法,bI,BI,FI和zI可以分别表示为

其中

如果将∆bI,∆BI,∆FI和∆zI分别看作围绕bc,Bc,Fc和zc的扰动,则可以采用第2 节所述参数摄动法求解区间哈密顿方程(40).

按照区间的含义,引入小参数ε,式(40)可以表示为:由于参数b存在小扰动δb,导致B,F和z产生小扰动δB,δF和δz,且满足

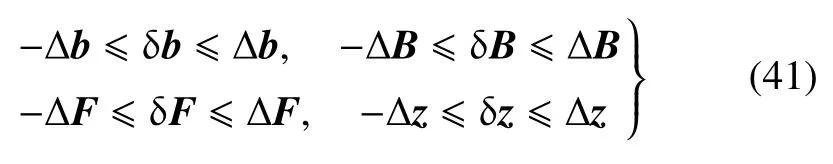
条件下的扰动方程的形式

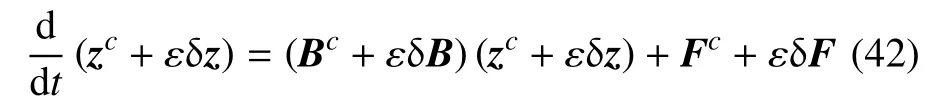
式(41)和式(42)所表示的问题可以理解为:在参数中值bc已知,从而能够确定中值Bc和Fc,而小扰动δb的具体取值未知但其取值范围(41)已知,小扰动δB和δF的具体取值也未知但其取值范围(41)可以确定的情况下,确定哈密顿系统的解z的界限.展开式(42)并比较ε 的同次幂系数,可得

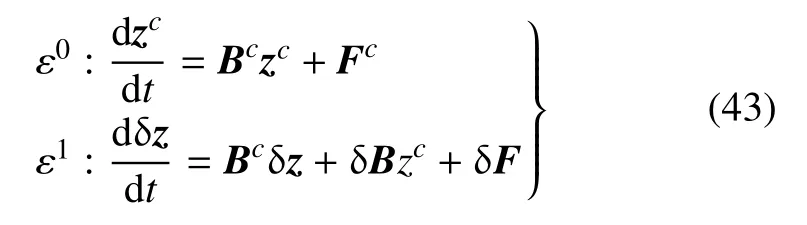
运用辛算法求解式(43)中第1 式可以求得z的中值zc.由区间扩张,式(43)中第2 式可写为

将z在z=zc处进行一阶Taylor 展开得到

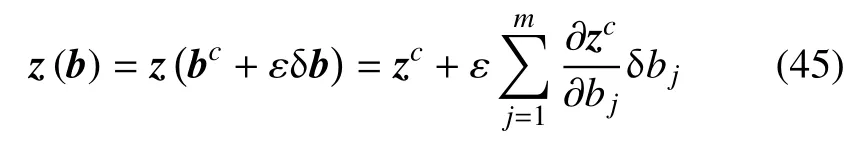
其中,δbj(j=1,2,···,m)是δb的分量.

从而可得δz的表达式

式(46)和式(47)的区间扩张形式为

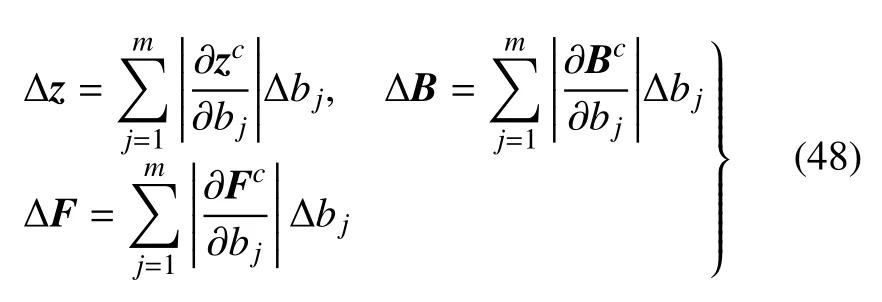
其中,∆bj(j=1,2,···,m)是∆b的分量.

将式(48)代入式(44),得

在计算求解过程中,求解式(43)中第1 式求得z的中值zc和求解式(49)求得z的半径∆z都采用了辛算法,同样确保计算结果能够保持体系结构特征.

由区间相等的定义可得z的上界和下界分别为

z的分量形式zi(i=1,2,···,2n)的上界和下界分别为

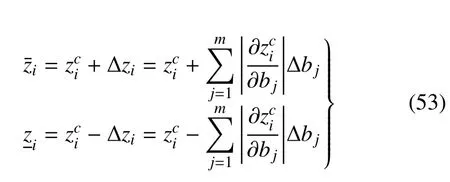
5 随机和区间非齐次线性哈密顿系统比较

不确定性是客观存在的,无论是随机方法还是区间方法,只是描述不确定性的不同形式,不能从本质上改变不确定性对响应的影响规律,利用两种方法得到的不确定性响应理应具有相容性.因此,本节对随机和区间非齐次线性哈密顿系统的分析结果进行比较,探究两者响应界限的包含关系.

假定参数b的区间范围由概率统计信息获取,即可以表示为距其均值距离为k倍标准差的形式

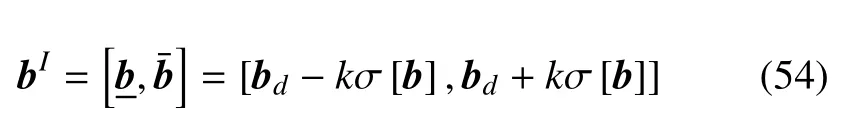
其中,k为正整数,σ[b]是b的标准差,b的上界和下界分别为

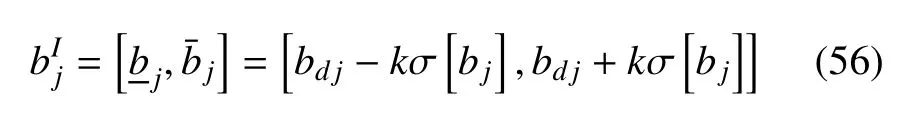
由式(54)∼式(55),可以得到参数b的区间中值和半径与随机确定性部分和标准差之间存在关系

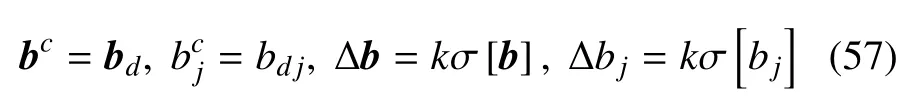
哈密顿系统的解z的区间中值与随机确定性部分同样存在关系

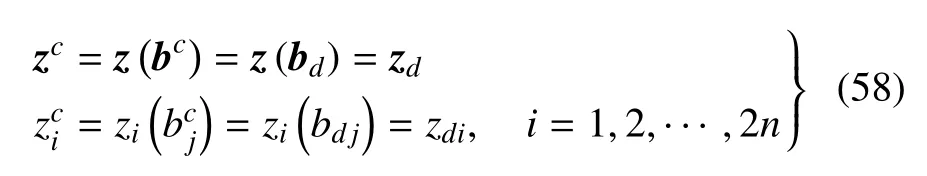
将式(57)的分量形式代入式(53),得到zi(i=1,2,···,2n)的上界和下界

对于参数bj,切比雪夫不等式成立

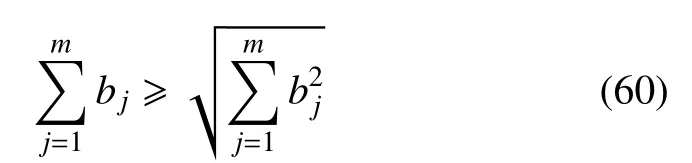
由不等式(61),可以得到由随机方法确定的上下界(34)和由区间方法确定的上下界(59)存在关系

式(62)表示,在由概率统计信息确定不确定性参数的区间范围的情况下,对于不确定性非齐次线性哈密顿系统,由区间方法获得的哈密顿系统的解的范围比由随机方法获得的范围大,即区间方法得到的上界比随机方法得到的上界大,而区间方法得到的下界比随机方法得到的下界小.

6 数值算例

为了验证所提方法在结构动力响应中的可行性和有效性,本节给出两个数值算例,包括悬臂梁和复合材料层合板,并将本文所提随机、区间方法(分别简记为SHPM、IHPM)计算结果与传统随机、区间方法(分别简记为TSM、TIM)计算结果相比较.

6.1 悬臂梁

考虑如图1 所示11 节点、10 单元悬臂梁在正弦激励作用下的动力响应.梁长L=1 m,横截面积A=2 cm2,横截面的惯性矩Iz=2 cm4,材料泊松比ν=0.3.正弦激励P(t)=−psin(1600πt)N 作用在节点3 的竖直方向,初始条件为˙x(0)=0,x(0)=0.

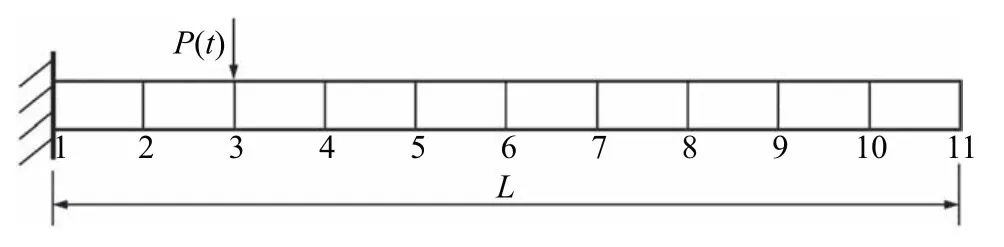
图1 11 节点、10 单元悬臂梁Fig.1 A cantilever beam with 11 nodes,10 elements

由于材料中不可避免的分散性及测量误差,材料的弹性模量、密度和正弦激励幅值均具有不确定性,假设它们所在的区间范围I如表1 所示;同时假设它们在区间范围内服从正态分布,均值µ 和标准差σ 也如表1 所示.

表1 材料弹性模量、密度和正弦激励幅值的不确定性Table 1 Uncertainties of elastic modulus,density of the material and the amplitude of the harmonic excitation

悬臂梁整体运动微分方程为

其中,M是悬臂梁整体质量矩阵,与材料密度ρ 有关;K是整体刚度矩阵,与材料弹性模量E有关;F(t)是整体载荷向量,与正弦激励P(t)有关.

令y=则整体运动方程(63)可以表示为

首先考察在时间步长∆t=40µs 下利用辛算法求解哈密顿系统(64)和直接求解方程(63)方法计算节点11 的响应标称值.利用辛算法求解哈密顿系统(64)计算得到的t=0∼0.1 s 内的响应标称值曲线如图2(a)所示,整体呈周期性变化,但直接求解方程(63)得到的响应标称值很短时间内即发散,如图2(b)所示,只有当时间步长足够小,如∆t=2µs 时,直接求解方程(63)才能得到和利用辛算法求解哈密顿系统(64)相同的结果.这一稳定性差异反映了哈密顿系统辛算法能够保持体系结构特征,体现出利用哈密顿系统辛算法求解微分方程的优越性.

图2 时间步长∆t=40µs 下利用不同算法计算得到的节点11 的响应标称值Fig.2 The nominal value of the response of node 11 obtained by different algorithms with time step ∆t=40µs

图2 时间步长∆t=40µs 下利用不同算法计算得到的节点11 的响应标称值(续)Fig.2 The nominal value of the response of node 11 obtained by different algorithms with time step ∆t=40µs(continued)

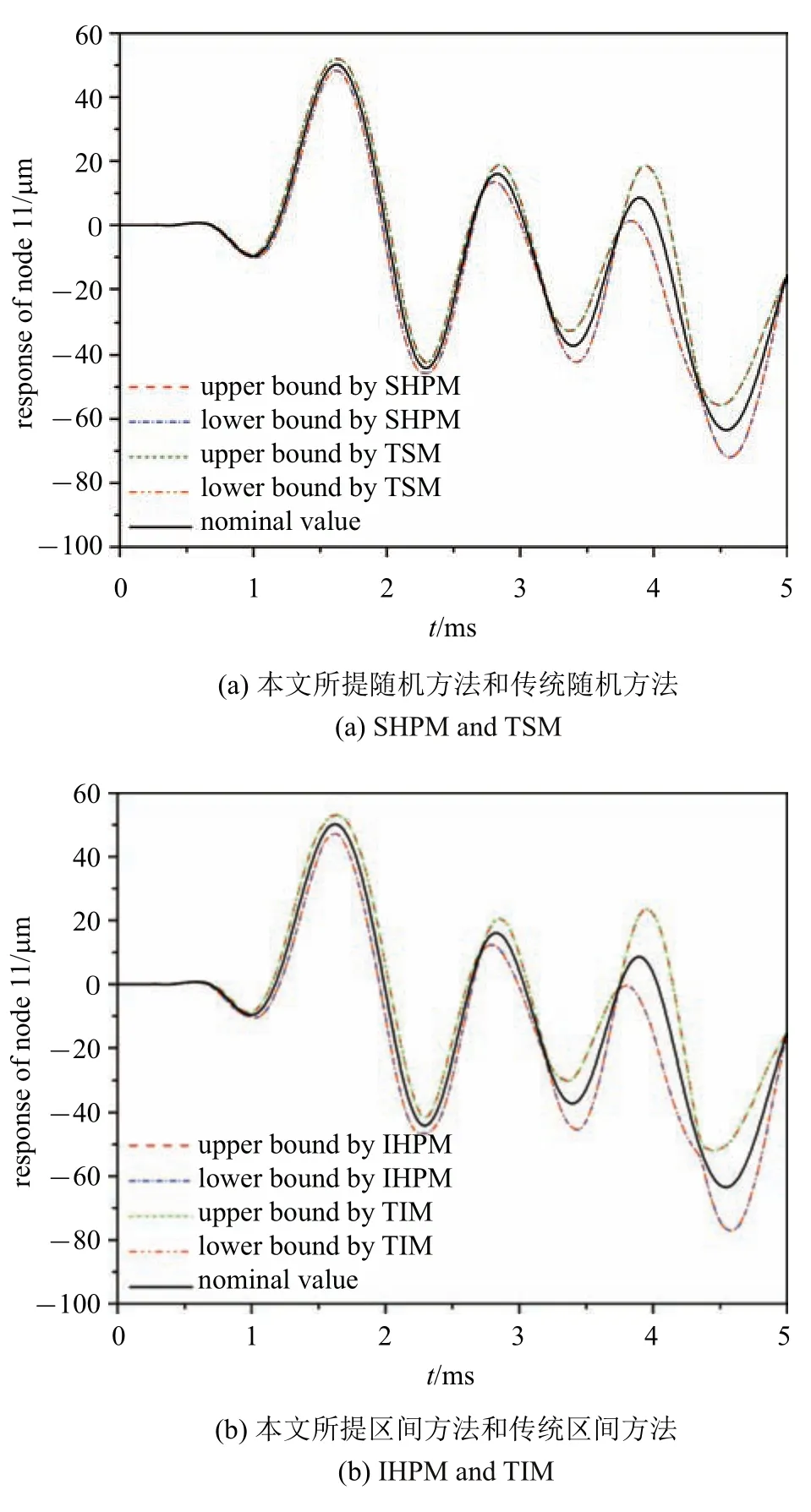
图3 本文所提方法和传统方法计算得到的节点11 的响应曲线Fig.3 The response curve of node 11 obtained by SHPM,IHPM,TSM and TIM

在同一时间步长∆t=2 µs 下本文所提随机、区间非齐次线性哈密顿系统的参数摄动法和传统随机、区间方法计算得到的节点11 在t=0∼5.0 ms 内的响应曲线如图3 所示,其中图3(a)∼图3(b)分别为两种随机、区间方法得到的响应曲线,图3(c)为本文所提随机、区间方法计算得到的响应曲线,响应标称值也绘制于图3 中.本文所提随机、区间方法和传统随机、区间方法计算得到的节点11 在t=3.5 ms 时刻的位移上下界如表2 所示.

表2 本文所提随机、区间方法和传统随机、区间方法计算得到的节点11 在t=3.5 ms 时刻的位移上下界Table 2 The upper and lower bounds on the displacement of node 11 at t=3.5 ms obtained by SHPM,IHPM TSM and TIM

由图3 和表2 可知,本文所提随机、区间方法得到的响应上下界曲线分别与传统随机、区间方法所得响应上下界曲线均几乎完全重合,结果非常相近,验证了所提随机、区间方法的准确性和有效性.此外,本文所提区间方法得到的响应区间范围包含本文所提随机方法得到的响应区间范围,即区间方法所得响应上界大于随机方法所得响应上界,而区间方法下界小于随机方法下界,这一现象与前述理论推导相符.

前述内容验证了在较大时间步长∆t=40µs 下哈密顿系统辛算法相较于直接求解运动微分方程方法计算响应标称值的有效性和优越性,也验证了在较小时间步长∆t=2µs 下本文所提随机、区间方法所得响应区间范围的准确性.为了进一步检验本文所提随机、区间方法在较大时间步长下所得响应区间范围也能保持较高精度,下面将本文所提随机、区间方法在时间步长∆t=40µs 下得到的响应区间范围与蒙特卡洛模拟方法(简记为MCM)得到的响应区间范围进行比较.其中,蒙特卡洛模拟在较小时间步长∆t=2µs 下进行,样本点数目设置为1.0×105,对于每一样本点都采用辛算法求解,从而可将蒙特卡洛模拟结果视为精确值.本文所提随机、区间方法和蒙特卡洛模拟方法计算得到的节点11 在t=0∼5.0 ms 内的响应曲线如图4 所示.

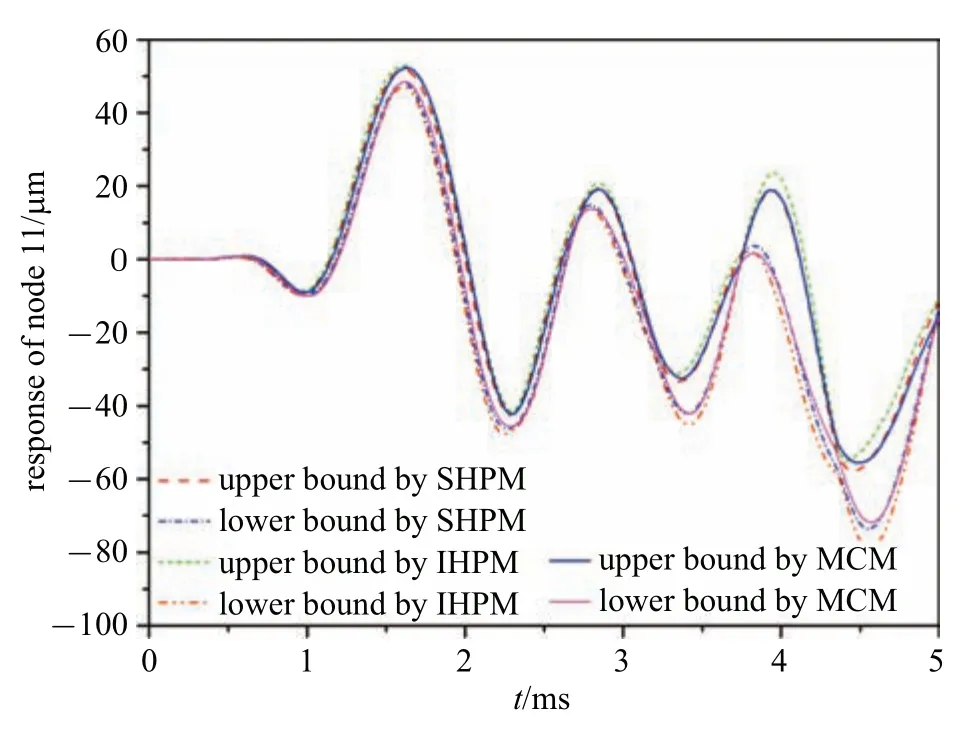
图4 本文所提随机、区间方法和蒙特卡洛模拟方法计算得到的节点11 的响应曲线Fig.4 The response curve of node 11 obtained by SHPM,IHPM and MCM

由图4 所示,本文所提随机方法与蒙特卡洛模拟方法得到的响应上下界曲线差别微小,尽管由于较大时间步长原因导致精度有一定下降,但仍得到了较为满意的结果.这一现象体现出本文所提方法在较大时间步长下也能得到具有较高精度的结果,再次验证了本文所提方法的优势.而对于本文所提区间方法,由于区间扩张效应,得到的响应区间范围包含本文所提随机方法和蒙特卡洛模拟方法得到的响应区间范围,与前述理论推导相一致.

6.2 复合材料层合板

考虑如图5 所示的边长为L=1.0 的四边固支的复合材料层合板结构,其由5 层正交各向异性材料铺设而成,铺设角度为(0◦,90◦,0◦,90◦,0◦),每层厚度为t=0.012,质量密度ρ=1.0.板中心处受一垂直于板的正弦激励作用P(t)=−psin(200πτ),初始条件为(0)=0,x(0)=0.材料属性和正弦激励幅值同样均具有不确定性,假设其区间范围I如表3 所示;同时假设它们在区间上服从正态分布,均值µ和标准差σ也如表3 所示.采用4 结点矩形薄板单元,将板划分为相等的16 个单元.为方便,所有数据均采用无量纲量.

图5 四边固支复合材料层合板Fig.5 A composite laminate with fully clamped boundary conditions

表3 材料属性和正弦激励幅值的不确定性Table 3 Uncertainties of material properties and the amplitude of the harmonic excitation

考虑板中心处z方向的动力响应.在同一时间步长∆τ=1.0×10−5下,本文所提随机、区间方法和传统随机、区间方法在τ=0∼0.05 内计算得到的响应范围以及响应标称值曲线如图6 所示,其中图6(a)∼图6(b)分别为两种随机、区间方法得到的响应曲线,图6(c)为本文所提随机、区间方法计算得到的响应曲线.本文所提随机、区间方法和传统随机、区间方法计算得到的τ=0.025 时刻位移上下界如表4 所示.

由图6 和表4 可知,本文所提随机、区间方法得到的响应上下界曲线分别与传统随机、区间方法所得响应上下界曲线同样近乎完全重合,再次验证了所提方法的有效性.同时,本文所提区间方法得到的响应上界比随机方法得到的响应上界大,区间方法得到的响应下界比随机方法得到的响应下界小,也与理论推导和算例6.1 现象一致.

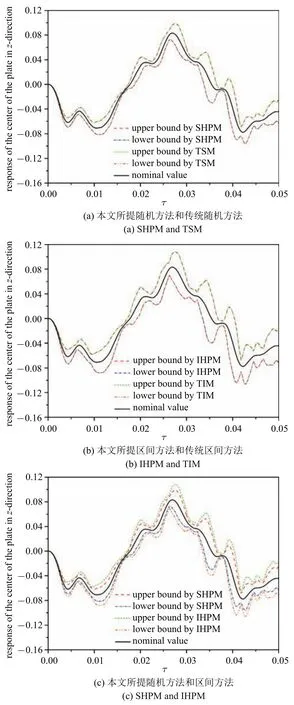
图6 本文所提方法和传统方法计算得到的板中心处z 方向的响应曲线Fig.6 The response curve of the center of the plate in z-direction obtained by SHPM,IHPM,TSM and TIM

下面进一步比较在时间步长∆τ=2.5×10−4下利用哈密顿系统辛算法和直接求解运动微分方程计算得到的响应标称值,曲线分别如图7(a)∼图7(b)所示.由图7 可知,利用哈密顿系统辛算法求解能够得到满意的响应标称值,然而在该时间步长下直接求解运动微分方程得到的响应标称值同样在很短时间内发散.这一现象再次体现了哈密顿系统辛算法由于能够保持体系结构特征而具有很好的稳定性,凸显了哈密顿系统辛算法在数值模拟中的显著优越性.

表4 本文所提随机、区间方法和传统随机、区间方法计算得到的板中心处z 方向在τ=0.025 时刻的位移上下界Table 4 The upper and lower bounds on the displacement of the center of the plate in z-direction at τ=0.025 obtained by SHPM,IHPM TSM and TIM

图7 时间步长∆τ=2.5×10−4 下利用不同算法计算得到的板中心处z 方向的响应标称值Fig.7 The nominal value of the response of the center of the plate in z-direction obtained by different algorithms with time step ∆τ=2.5×10−4

7 结论

本文考虑非齐次线性哈密顿系统,基于摄动理论发展了含小参数扰动的哈密顿系统的参数摄动法,以此为基础分别将小扰动看作随机、区间扰动,提出了分别针对随机、区间不确定性哈密顿系统的参数摄动法,突破了传统哈密顿系统的限制,并由切比雪夫不等式证明了两者响应分析结果的相容性关系,通过两个综合考虑外载荷和不确定性的结构动力响应数值算例验证得到了如下结论:

(1)在同一较大时间步长下,由直接求解运动微分方程的方法得到的响应标称值很可能会发散,而将运动微分方程引入到哈密顿系统后再利用辛算法计算仍然可以得到令人满意的结果,体现了哈密顿系统辛算法具有很好的稳定性,保持体系结构特征的优势明显,在数值仿真模拟方面的显著优越性;

(2)在同一较小时间步长下,本文所提随机不确定性哈密顿系统的参数摄动法得到的响应上下界分别与传统随机方法所得响应上下界结果近乎完全一致,差别微小,本文所提区间方法得到的响应上下界也分别与传统区间方法所得响应上下界极为相近,验证了所提方法的有效性;

(3)本文所提随机方法在较大时间步长下得到的响应上下界与蒙特卡洛模拟方法在较小时间步长下得到的响应上下界基本吻合,说明本文所提方法在较大时间步长下也能得到具有较高精度的结果,再次验证了本文所提方法的优越性;

(4)当参数的区间范围由概率统计信息确定,即区间半径表示为距其均值距离为标准差的整数倍时,本文所提区间方法计算得到的响应区间范围包含本文所提随机方法计算得到的响应区间范围,即区间响应上界大于随机响应上界、区间响应下界小于随机响应下界.