基于ARMA模型预测我国货币供应量M1

张雨 许学军

摘 要：货币供应量M1作为一个重要的先行指标，反映了经济周期和价格的波动。严密监测与调控货币供应量M1对抑制通货膨胀和促进经济健康增长具有重要的意义。因此，正确预测货币供应量M1的变动显得尤为重要。以我国货币供应量M1从2018年4月至2020年4月的月度数据为样本，通过Eviews统计软件，构建货币供应量的ARMA模型，经检验拟合效果较好且模型预测误差较小，最后利用该模型对未来3个月（2020年5—7月）的货币供应量M1进行预测。

关键词：时间序列;ARMA模型;货币供应量

中图分类号：F820        文献标志码：A      文章编号：1673-291X（2020）36-0052-03

引言

货币供应量M1反映了货币供给的活化程度，其与经济的微观预期及经济的基本面息息相关。其作为經济基本面的领先指标，引起了人们的高度重视和广泛研究。货币供应量作为一个时间序列，数据之间具有合乎规律的连续性。在一定条件下，如果未来期间整体的经济环境没有发生巨大的变化，货币供应量的基本发展趋势还会延续下去，所以可以建模来分析其中的规律。

ARMA模型是研究时间序列平稳随机过程的典型方法，将此模型运用到货币供应量M1的预测，可以降低预测误差。因此，本文以货币供应量M1的历史数据为样本，通过建立ARMA模型预测未来3个月的货币供应量M1。

一、模型理论介绍

（一）ARMA模型简介

自回归移动平均模型ARMA主要应用于对一维、方差恒定的时间序列进行分析，认为时间序列当年观测项的值可以表示为之前的p项观测值及q项随机误差的线性组合，如式（1）所示，记作ARMA（p，q）模型。

其中，Xt与前p期的序列值有关，还与前q期的随机干扰有关，εt为噪声，称时间序列{Xt}为p阶自回归移动平均模型。p是自回归阶数，q是移动平均阶数，Φi（i=1，2，…，p）是自回归参数，θj（j=1，2，…，p）是移动平均参数。

（二）ARMA模型的平稳性检验

当时间序列不平稳时，不能直接运用ARMA模型。因此收集和预处理数据之后，要对数据进行平稳性检验。对ARMA模型进行平稳性检验常用的方法是单位根（ADF）检验法。首先对式（2）进行回归分析：

根据回归分析的结果，分析ADF检验的t统计量和其所对应的P值，如果P值在相应的置信区间内显著，就表明可以拒绝原假设，认为该时间序列是平稳的。反之，若不能拒绝原假设，就可以判断该时间序列是非平稳的，此时要对数据进行处理使其平稳。

（三）ARMA模型的类型和滞后阶数

ARMA模型的具体类型是依据（偏）自相关系数的形态决定。若时间序列的偏自相关系数与其自相关系数都呈现拖尾形态，则可以使用ARMA（p，q）建立模型，并可以根据（偏）自相关系数粗略的估计滞后阶数。当根据相关系数难以确定p和q滞后的阶数时，需要结合信息准则来判断。即当p和q达到某一组数值时，AIC（p，q）、SC（p，q）和HQ（p，q）达到最小值时的p和q为最佳的模型阶数。

二、我国货币供应量M1的实证分析及预测

（一）数据选取

本文以我国货币供应量M1从2018年4月至2020年4月的月度数据作为样本，数据来源于东方财富网数据中心。通过Eviews统计软件，运用ARMA模型构建了关于货币供应量M1的预测分析模型。

（二）数据的单位根检验

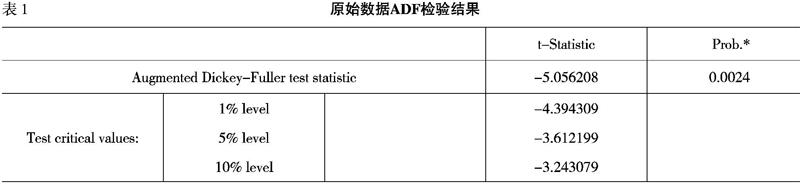
数据的平稳性检验是建立模型的基础，检验平稳性经常使用的是单位根（ADF）检验法。使用Eviews统计软件对原始数据进行单位根检验（如下页表1所示），ADF检验的t统计量小于1%显著性水平下的临界值，故该序列数据是平稳的，可以利用此数据建立模型。

（三）识别模型形式

在验证原始数据是平稳的时间序列之后，我们需要观察自相关和偏自相关系数图来识别模型的形式，并结合信息准则判断模型的滞后阶数。

从下图左侧可以看出，货币供应量M1的自相关和偏自相关都具有拖尾的形态，初步确定可以使用ARMA模型对货币供应量M1进行预测分析，同时结合信息准则来进一步预测该模型的滞后阶数。

由于样本（偏）自相关系数在滞后一阶的时候明显超过两倍标准差的界限，但从滞后两阶开始几乎所有的（偏）自相关系数都在界限之内，所以暂时粗略的估计滞后两阶。又因为通常情况下，ARMA模型的滞后阶数不会太大，故选取ARMA（1，1）、ARMA（1，2）、ARMA（2，1）、ARMA（2，2）这四种情形进行回归分析，结果（如表2所示）。根据信息准则，比较AIC（p，q）、SC（p，q）、HQ（p，q）的值可以得出，p=1和q=1为最佳的模型阶数，此时的ARMA（1，1）为最佳的模型。

同时，观察ARMA（1，1）回归分析的结果（如下页表3所示），各系数都在99%的置信区间内显著，所以我们选ARMA（1，1）模型对我国货币供应量M1进行建模。

（四）建立模型

结合信息准则和回归分析的结果可以确定拟合度较好的预测模型是ARMA（1，1）。从下页表3回归分析的结果中可以得知，该模型的参数估计值中AR（1）的t统计量为15.69476，其对应的P值为0.00;MA（1）的t统计量为-16.62485，其对应的P值为0.00，都在99%的置信区间内显著，因此其对应的模型表达式为：

Xt=29625.3755+0.9487Xt-1+εt-0.9479εt

接下来，对ARMA（1，1）回归模型进行残差检验，从回归方程的残差图中可以得出，均方误差度较小，残差序列样本的绝对值与均方误差区间差异较小。因此可以认为，模型ARMA（1，1）估计结果的残差序列不存在自相关。

（五）模型预测

对拟合模型2019年10月至2020年4月的数据进行静态预测，得出曲线均在有效区间内，且模型预测值基本和差分序列图拟合。进一步验证，本文建立的模型较为准确，可以运用此模型进行预测。最后，通过ARMA（1，1）模型对未来3个月货币供应量M1进行模型差分预测，预测差距值的相对变动率在3%之内。经计算调整后，暂估未来3个月货币供应量M1（以億元为单位）依次为573 630、562 500、584 640。

结语

本文利用时间序列分析的建模思想，对我国货币供应量这一时间序列进行实证分析。本文的整体思路如下：首先，对样本序列进行平稳性检验，在保证平稳性的基础上，根据相关系数和信息准则来估计模型的滞后阶数。其次，利用最小二乘法估计模型的参数，并检验残差是否存在自相关。最后，通过拟合预测值和实际值验证模型的可靠性，并以此来预测未来3个月的货币供应量M1。

综上所述，ARMA模型充分利用有限的数据集对未来的发展趋势进行了预测分析。通过ARMA模型进行建模和实证分析得到的短期货币供应量M1的预测值较为理想，为学者分析经济周期和价格波动提供了一定的参考意义。

参考文献：

[1]  张思奇，马刚，冉华.股票市场风险、收益与市场效率：——ARMA-ARCH-M模型[J].世界经济，2000，（5）：19-28.

[2]  郭雪，王彦波.基于ARMA模型对沪市股票指数的预测[J].Economic&TradeUpdate，2006，（4）：58-59.

[3]  李美威，谢小鹏，冯伟，贺石中.基于ARMA模型的在线油液监测故障预警研究[J].润滑与密封，2019，（12）：108-113.

[4]  陈易平，俞龙，谌颃.大数据环境下基于小波神经网络和ARMA模型的流量异常检测[J].重庆理工大学学报：自然科学版，2019，（10）：149-154.

[5]  蔡承智，黄军结，梁颖.基于ARIMA模型的世界大豆总产预测分析[J].大豆科学，2019，（2）：298-303.

[6]  邓军，杨宣，王玮，等.运用ARMA模型对股价预测的市政研究[J].企业导报，2010，（6）：266-267.

[7]  徐晨萌，方华.运用ARMA模型对股价预测的实证研究[J].经济研究导刊，2019，（31）：77-82.