立体几何情境中的最值问题

广东省广州大学附属中学(510006) 曹 勇

近几年全国卷越来越注重对立体几何的考查，特别是选择填空题中，立体几何频繁出现在试卷难度较大的12，16 题的位置，其中最值问题是非常重要的一个考查方向.最值问题综合性较强，主要有几何法和代数法两个解题方向，几何法侧重利用平面几何知识求最值，代数法侧重利用函数求最值.本文总结了立体几何情境中几种主要的最值题型与解法，供同行参考.

一、平面展开求最值

例题1已知三棱锥P -ABC中，PA ⊥平面ABC，其三视图是由三个直角三角形构成，如图1所示，若点M,N分别在棱PB,PC上，则AM+MN+NA的最小值为( )

图2

分析通过三视图，画出三棱锥P -ABC的直观图，空间中长度之和的最值问题，通常通过平面展开、旋转，将几段长度转化到同一个平面，进而转化为平面几何中两点之间距离最短问题，最后利用平面几何知识计算得到答案.

解通过三视图，画出三棱锥P -ABC的直观图，如图2所示，以∆PCB为初始平面，将∆PCA,∆PBA分别沿边PC,PB展开并旋转，使之与∆PCB所在平面共面，如图3所示，则AM+MN+NA的最小值即为线段AA1的长，根据平面几何知识所以所以AA1=6，即AM+MN+NA的最小值为6.

真题某圆柱的高为2，底面周长为16，其三视图如图4．圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为( )

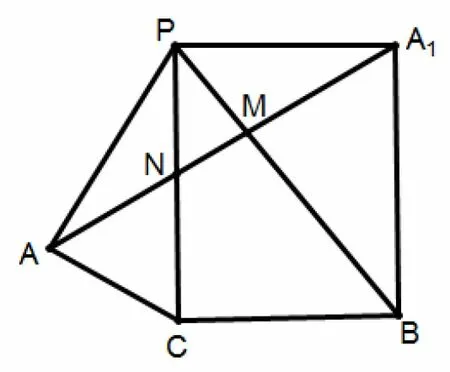
图3

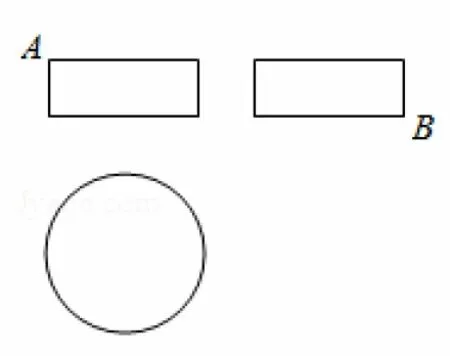
图4

简析此题为2018年全国Ⅰ卷考试题，求曲面上两点之间最短距离，使用平面展开的方法，易得答案为

二、平面平移求最值

例题2如图5，在四面体ABCD中，AB=CD=2,E,F分别是AD,BC中点.若用一个与直线EF垂直，且与四面体的每一个面都相交的平面α去截该四面体，由此得到一个多边形截面，则该多边形截面面积最大值为..

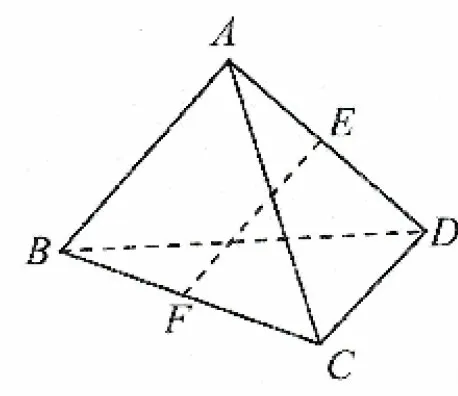
图5

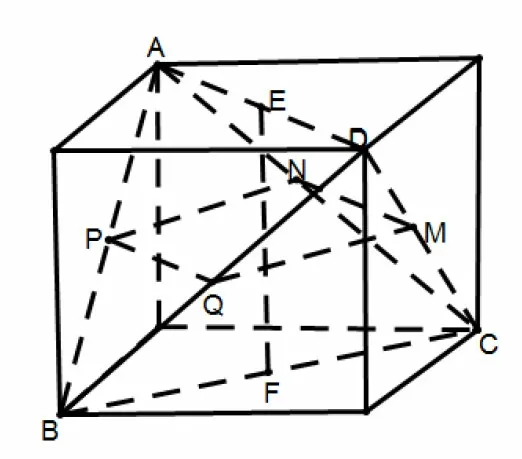
图6

分析若直接找平面α，很难操作，且不易观察何时截面面积最大.注意到四面体ABCD中三组对边分别相等，可以在长方体中构造四面体，再找截面α将会非常方便直观，并在截面平移过程中，利用平面几何知识，对称性，函数思想等相关知识求最值.解决此类问题，先找出满足条件的截面，再平移截面找最值是基本解题思想.

解在长方体中构造四面体ABCD，如图6所示，与直线EF垂直的截面α，即为平行四边形PQMN，即求截面PQMN平移过程中面积的最大值.平移过程中始终有设异面直线BC与AD的夹角为θ，则当且仅当PQ=PN时取等号，此时截面过四面体ABCD各边中点.

真题已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为( )

简析此题为2018年全国Ⅰ卷考试题，当截面平移到正方体各边中点，形成正六边形时面积最大值为

三、动点轨迹求最值

例题3如图7，正方体ABCD-A1B1C1D1中，E是DD1的中点，F是侧面CDD1C1上的动点，且B1F ‖平面A1BE，则B1F与平面CDD1C1所成角的正切值的最大值是.

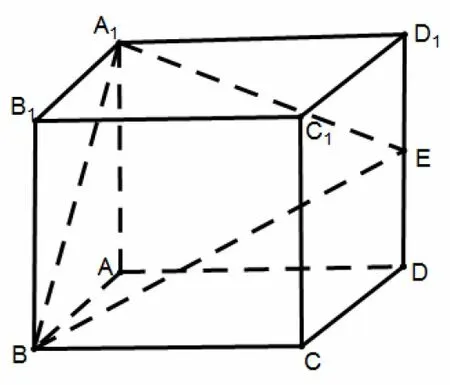
图7

图8

分析要求B1F与平面CDD1C1所成角的最大值，需先找出动点F的运动轨迹，本题是线面平行背景的动点轨迹问题，要找线面平行，先找面面平行，要使得B1F ‖平面A1BE，则平面A1BE ‖B1F所在的平面，找到B1F所在的平面即找到P点的运动轨迹.

解如图8所示，分别取线段CC1,C1D1中点M,N，连接B1M,B1N,MN，则平面B1MN ‖平面A1BE，所以动点F的轨迹即为线段MN.B1F与平面CDD1C1所成角即为∠B1FC1，所以显然当C1F最小，即C1F ⊥MN时∠B1FC1最大，设正方体边长为a，则所以tan ∠B1FC1最大值为

例题4在棱长为1 的正方体ABCD-A1B1C1D1中，E是AA1的中点，P是∆BDC1内的一个动点，EP ⊥BC1，则EP的最大值为.

分析需先找出动点P的运动轨迹，本题是异面直线垂直背景的动点轨迹问题，要找线线垂直，先找线面垂直，要使得EP ⊥BC1，则BC1⊥EP所在的平面，找到平面即找到P点的运动轨迹.

解如图9所示，连接AC,BD交于点M，连接A1C，过M作MN ⊥ BC1，垂足为N，再连接EN.正方体ABCD - A1B1C1D1中，A1C ⊥平面BDC1，所以EM ⊥平面BDC1，所以EM ⊥BC1，又MN ⊥BC1,所以BC1⊥平面EMN，平面EMN即为所求平面，线段MN即为动点P的轨迹.在Rt∆EMN中所以EP的最大值为

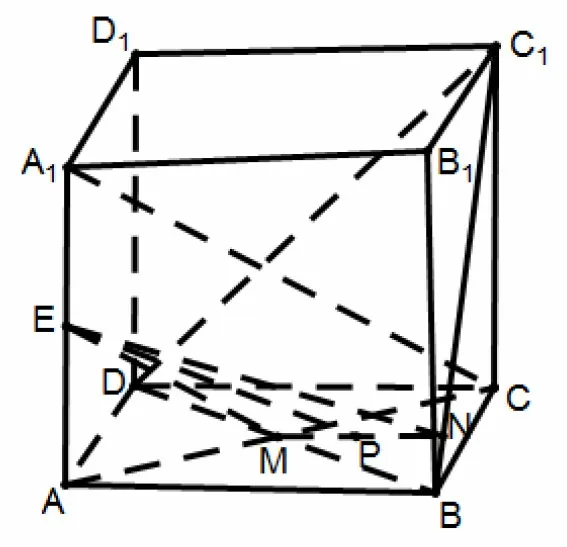
图9

四、内切、外接求最值

例题5有一个底面半径为R，轴截面为正三角形的圆锥纸盒，在该纸盒内放一个棱长均为a的四面体，并且四面体在纸盒内可以任意转动，则a的最大值为.

分析要使得四面体在纸盒内可以任意转动，则四面体要在圆锥纸盒的内切球O内转动，要使得棱长a最大，则内切球O应为四面体的外接球.在求解内切球问题时，利用截面图形的相似，是刻画内切球半径的常用方法.

图10

解圆锥纸盒及其内切球O的轴截面图形如图10所示，设球O半径为r，则OE=r,BD=R, AB=2R,所以所以又棱长为a的正四面体外接球半径所以所以a的最大值为

例题6三棱锥P-ABC中，底面∆ABC满足BA=P在 面ABC的射影为AC的中点，且该三棱锥的体积为当其外接球的表面积最小时，P到面ABC的距离为( )

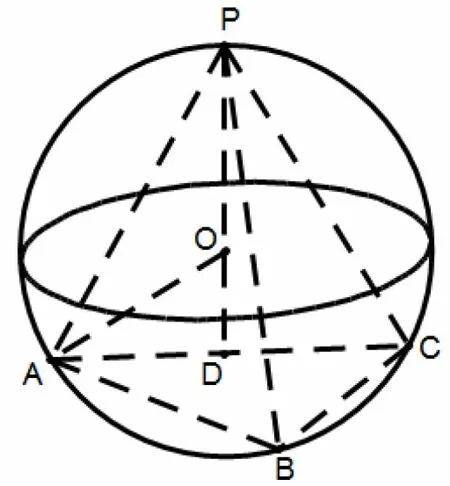
图11

分析外接球的表面积最小即外接球半径最小，需先构建外接球半径的函数，通过函数刻画取最值的条件，在解外接球问题时，如何找到外接球的球心，进而刻画半径是解题关键，这需要学生熟练掌握常见外接球半径的求解方法.

解如图11 所示，设P在底面的射影为D，则D为AC中点，外接球球心O在PD上，连接OA，则OA为外接球半径R，PD为P到面ABC的距离，设AB=BC=a，PD=h，则有所以a2h=27.由OA2=OD2+AD2，得化简得

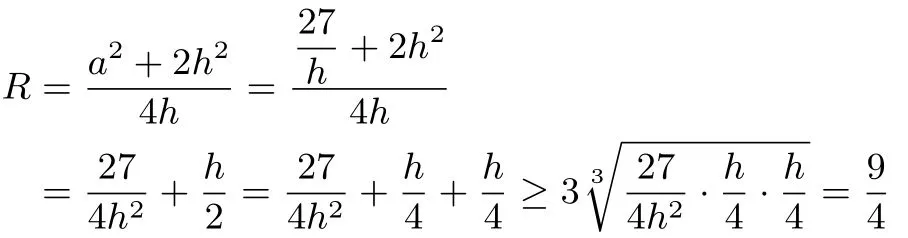
五、体积问题求最值

例题7已知在四面体A - BCD中，AD=DB=AC=CB= 1，则该四面体体积的最大值为.

分析体积最值问题中找到几何体的高是解题关键，也是难点，然后选择与动点相关的边或角作为变量，并将几何体的底面积和高用变量刻画，从而构造体积与变量的函数，最后利用函数知识求最值.

图12

解如图12 所示，取AB中点E，连接CE,DE，则CE ⊥AB,DE ⊥AB，所以AB ⊥平面CDE，设AE=x，则AB=2x,所以

S∆CDE=sin ∠CED,因此

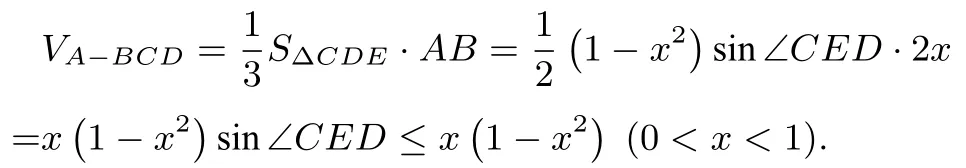
真题如图13，圆形纸片的圆心为O，半径为5 cm，该纸片上的等边三角形ABC的中心为O.D,E,F为圆O上的点，∆DBC,∆ECA,∆FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后，分别以BC,CA,AB为折痕折起∆DBC,∆ECA,∆FAB，使得D,E,F重合，得到三棱锥.当∆ABC的边长变化时，所得三棱锥体积(单位： cm3)的最大值为.

图13

简析此题为2017年全国1 卷考试题，连接OF交AB于P，设OP=x, PF= 5- x，三棱锥高为构造体积关于x的函数利用导数易得x= 5 时，三棱锥体积的最大值为

本题中如果设三角形ABC边长为x，计算量将会加大，可见体积最值问题中，如何设变量，也是解题的关键.

立体几何情境中的最值问题不仅考查学生的立体几何知识，还考查学生的平面几何知识，以及函数，导数，不等式等代数知识，是空间与平面，代数与几何的有机结合体，能充分考查学生多方面的数学素养，这也是高考试题频繁出现的原因.要解决好此类问题，不仅需要学生扎实掌握相关知识，还需要我们教师积极引导学生总结最值问题的主干题型和解法，本文旨在抛砖引玉，请不吝赐教！