基于波利亚解题理论求解2019年全国Ⅰ卷22题*

华南师范大学数学科学学院(510631) 陈俊阳 黄晓湄

将曲线参数方程转化为普通方程的题型活跃在历年高考的全国卷中，广东考生近四年在理科卷第22 题的得分情况如下： 2016年平均分为6.71 分，2017年为5.27 分[1]，2018年为5.23 分，但2019年仅有3.53 分.得分大幅度下降的主要原因是参数方程的形式异于常规，涉及到难度较大的消参技巧[2]，导致部分学生无法形成正确的解题思路.美国著名的数学教育家波利亚提出的波利亚解题理论有利于解题思路的形成和问题的求解.本文将运用波利亚的解题表给出的弄清问题、拟定方案、执行方案、回顾反思的方法[3]，分析思路的形成过程，求解2019年全国Ⅰ卷第22 题.

一、原题呈现

题目(2019年高考全国Ⅰ卷第22 题)在直角坐标系xOy中，曲线C的参数方程为(t为参数).以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为

(1)求C和l的直角坐标方程;

(2)求C上的点到l距离的最小值.

注记本文只针对(1)中求曲线C的普通方程进行详细剖析.

二、试题剖析

(一)弄清问题波利亚说：“如果学生还没有弄清问题，就着手计算和做题，那就可能发生最糟的事了.对你所不理解的问题做出答复是愚蠢的.”因此，弄清问题是问题解决的基础.

1.未知量是什么? 曲线C的普通方程，即关于x,y的方程.

2.已知量是什么? 曲线C的含参数t的参数方程.

3.隐含条件是什么? 为防止出现多解或漏解的情况，应当考虑x,y其中之一的取值范围，

(二)拟定方案

拟定方案是帮助我们发散自身思维、探索解题思路的重要过程.在这一环节中，我们将通过回答不同的问题，以形成解题方案.

1.你知道与它有关的题目吗?

我们联想到： ①2017年全国Ⅰ卷22 题： 已知曲线C的参数方程为; ②人教版A 版必修4-4一道例题： 已知曲线C的参数方程为两题均求曲线C的普通方程.对①： 利用三角恒等式sin2α+ cos2α= 1 进行消元; 对②： 利用代入消元.本质上都是用x,y表示参数，进而消去参数得到曲线的普通方程.由此形成以下解题方案：

方案1： 将t代入消元.

方案2： 将t2代入消元.

2.观察未知量，并尽量想出一道你所熟悉的具有相同或相似未知量的题目! 为了有可能利用已知量，你是否应该引入某些辅助元素?

(1)观察x,y表达式，由1 +t2我们联想到恒等式为了利用之考虑引入辅助元素，即换元.由此形成以下解题方案：

方案3： 引入辅助元素，设t=tanθ,用θ分别表示x,y.

3.你能联想到与未知量相关的定理和公式吗?

(1)观察题目已知量，所给参数方程的形式与我们熟知的正切半角公式(下称“万能公式”)cosθ=的形式相仿，由此形成以下解题方案：

(2)此外，我们还能联系到古希腊数学家丢番图提出的勾股数的公式： 若a,b,c为直角三角形三条边长，c为斜 边，则有a= 2mn,b=m2- n2,c=m2+n2，其中m ＞n ＞0，且均为整数，它们满足a2+b2=c2.注意到条件中： 1-t2,1+t2,2t，这三个数恰好构成勾股数组.由此形成以下解题方案：

方案6： 利用丢番图勾股数公式： (1-t2)2+(2t)2=(1+t2)2.

4.回到定义上去

根据参数方程定义，取参数的不同值，得到曲线C上若干个点，运用描点法画出C的大致形状，猜想C的曲线类型，写出其曲线方程，并严谨地证明之.形成以下解题方案：

方案7： 通过定义，大胆猜想，小心求证.

(三)执行方案

解法1(将t代入消元)

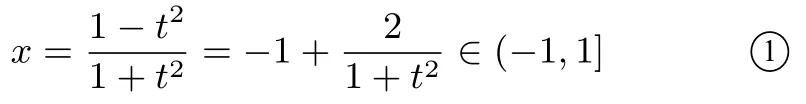
解法2(将t2代入消元)

解法3(引入辅助元素，设t=tanθ,用θ分别表示x,y)

事实上，这与方案5 相仿，方案执行详见解法5.

当t= 0 时，当0 时，由此解得代入x2并整理得把x=1,y=0 代入也成立，故C的普通方程为

解法6(利用丢番图勾股数公式)

注意到恒等式(1-t2)2+(2t)2=(1+t2)2，从而

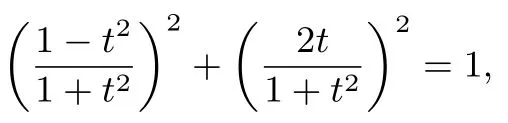
于是C的普通方程为

解法7(通过定义，大胆猜想，小心求证)

分别令t=0,1,-1,2,-2，可得曲线C上的点(1,0),(0,2)，(0,-2),在直角坐标系中描点如图1，根据点的分布猜想曲线C为焦点在y轴，半长轴为2，半短轴为1的椭圆，并进行验证：即得

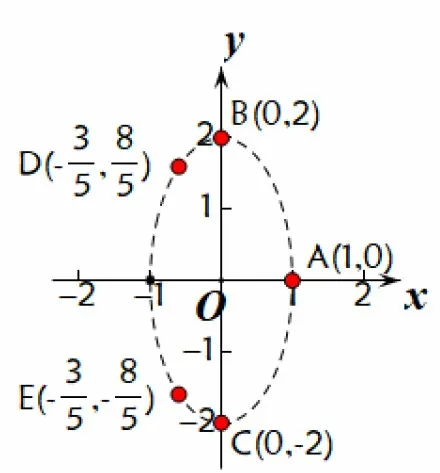
图1

(四)回顾反思

1.你能否检验这个论证? 由于参数方程与普通方程代表同一条曲线，这意味着两者之间的转化应为等价转化.如在方案1 及方案2 中，均有一步需对等式两边同时除以1+x，这一步是等价转化的条件为1，容易被忽略.因此，在解题时需对所解决问题涉及的知识内涵及对所用思想方法的本质认识准确[4]，这样才能大大减少漏解或多解的可能.

2.为什么出现了多解(或漏解)的情况? (1)一方面，对于一般问题，出现多解本质上是由于每一步的转化并非等价(若步步等价，得到的答案必定是正确的，不会多解或漏解)，而造成转化不等价的原因是做题过程中忽视了部分隐含条件.(2)另一方面，对于本题来说，为何会出现多解的情况，即普通方程要为何需去掉x=-1 的点? 下面提出两个定义及一个相关定理：

定义1[5]设曲线的参数方程为若极限均存在，且有

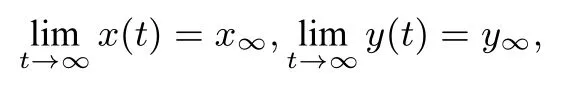
其中，x∞,y∞均为有限数，则称点(x∞,y∞)为曲线的参数无穷大点(事实上它是坐标平面上的一个有限点).

定义2[5]设t0为曲线参数方程定义域内任意一点，则称点(x(t0),y(t0))为参数方程的有限点.

定理1[5]若曲线的参数无穷大点存在，且不与任何参数有限点重合，则参数无穷大点不是曲线上的点(注： 证明详见参考文献[2]).

根据定理结合本题可知，由于

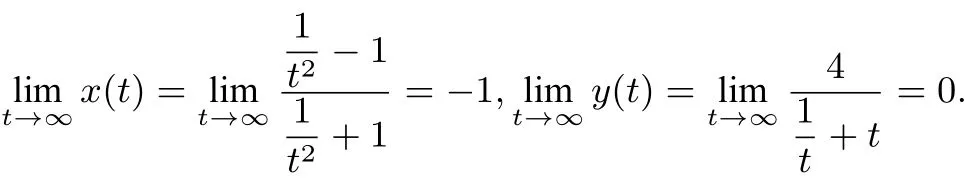
故点(-1,0)是曲线C的参数无穷大点，即当时有而易求得方程组无解，由此可知点(-1,0)不在曲线C上，故曲线C的参数方程转化为普通方程后，必须有x-1，这样才能防止多解的情况.

反思和总结虽然在做题时不必像上面一样求极限、求曲线的参数无穷大点以判断转化的等价性，只需考虑自变量的取值范围即可.但在做题后的回顾与反思阶段，若我们能对上面造成增解的原因进行深入反思和总结，并得出以上定理，那么我们在面对其他相似的题目时就能将问题看得更透彻，进而能从容面对其他的增解或漏解问题.

3.你能不能把这结果推广到一般情形? 由方案5 中的“万能公式”，本题可作初步的推广：

推广1 若曲线C的参数方程为(参数t ∈-∞,+∞)，常数a,b ＞0)则曲线C的普通方程为

更一般地，下面推广揭示了(椭)圆的普通方程与参数方程(x,y都是关于t的有理函数的情形)之间的关系：

推广2 若曲线C的参数方程为(参数t ∈-∞,+∞)，常数a,b ＞0)则曲线C的普通方程为

推广3 若曲线C的参数方程为(参数t ∈-∞,+∞)，常数a,b ＞0)则曲线C的普通方程为

反思和总结以上拟定和执行的多种方案各显神通，既能为解题提供帮助，也能为试题推广提供有力的思路和手段.此外，对原题中的结论进行推广可以深化我们对相关概念、方法和结论的理解，做到举一反三，融会贯通.这既有利于学生了解这一类问题的本质，又可以为教师提供命制此类试题的方向.