2019年高考北京卷理科第18题的探究与推广

广东省湛江一中培才学校（524037） 魏 欣

一道高考解析几何试题的命题背景可能就是圆锥曲线的一个性质定理的特殊情况.如果掌握了定理的原理，也就把握了试题的本质.对一些典型的试题，不应满足于会解，可以引导学生深入探究试题背后的知识背景，挖掘问题的本质.这样才能真正找到解决问题的方法，学会用更高观点去看待数学问题，把握问题的本质.正如《普通高中数学课程标准(实验)》所倡导的数学探究性课题学习，引导学生围绕某个数学问题，观察分析，自主探究，提出有意义的数学问题，探求适当的数学结论或规律.以下是引导学生从2019年高考北京卷理科第18 题出发，探究圆锥曲线的性质，揭示问题的本质.

一、试题展示与评析

题目(2019年高考北京卷理科第18 题)如图1所示，已知抛物线C:x2=-2py经过点(2,-1).

(Ⅰ)求抛物线C的方程及其准线方程： (Ⅱ)设O为原点，过抛物线C的焦点作斜率不为0 的直线l交抛物线于两点M,N，直线y=-1 分别交直线OM,ON于点A和点B.求证： 以AB为直径的圆经过y轴上的两个定点.

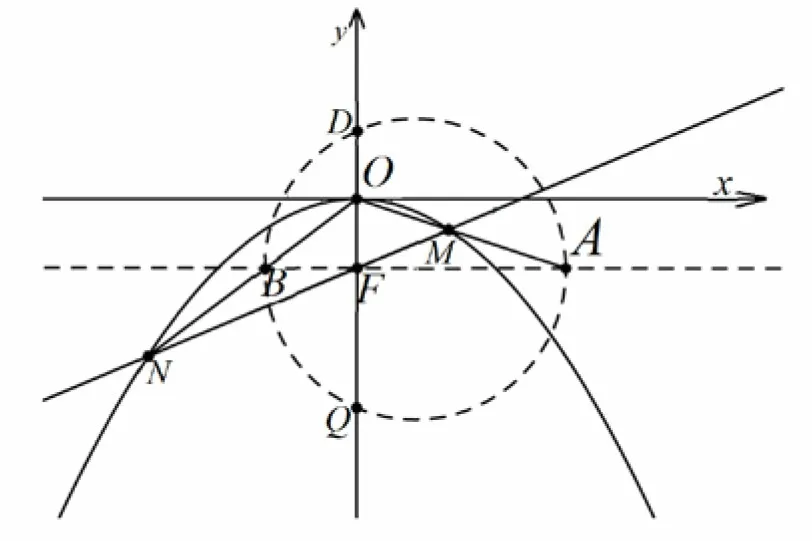
图1

解(Ⅰ)将(2,-1)代入x2=-2py，得22=-2p×(-1)，即p= 2.所以抛物线C的方程为x2=-4y，准线方程为y=1.

(Ⅱ)证法一如图1，直线l过抛物线C的焦点F(0,-1)，并交于抛物线C于M,N两点，所以直线l的斜率必存在.设直线l方程为y=kx -1 (0),M(x1,y1),N(x2,y2).由整理得x2+4kx-4=0.则从而，y1+y2=k(x1+x2)-2=-4k2-2, y1y2=直线OM,ON方程分别为则设以AB为直径的圆经过y轴上的定点坐标为D(0,n)，则因为故解得n= 1 或n=-3.故以AB为直径的圆经过y轴上的两个定点(0,1)和(0,-3).

证法二同证法一，可得AB的中点为

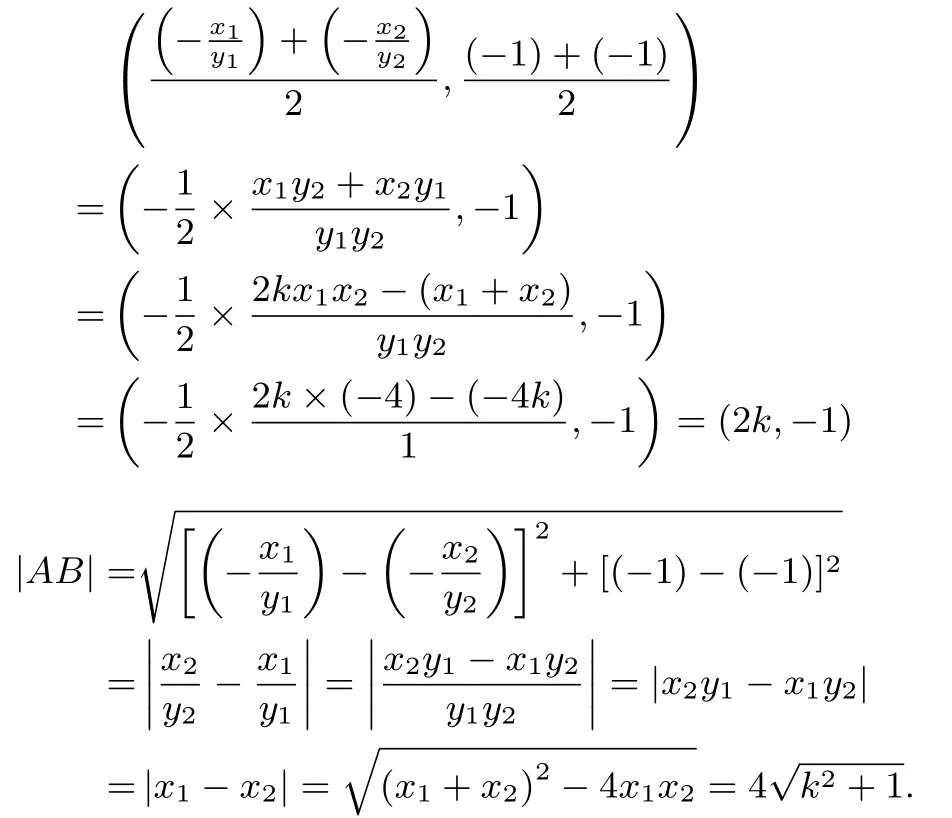
则以AB为直径的圆的半径为且其圆心为AB的中点(2k,-1).故以AB为直径的圆方程为(x -2k)2+ (y+ 1)2= 4(k2+ 1).整理得-4xk+x2-3+2y+y2= 0.由于该方程对任意0 恒成立，所以x=0.故y=1 或y=-3.故以AB为直径的圆经过两个定点(0,1)和(0,-3).

证法三以AB为直径的圆只经过y轴上两个定点，不再有其他的特殊点.假设直线l斜率为0，此时以AB为直径的圆方程为x2+(y+1)2= 4，过点(0,1)和(0,-3).假设直线l斜率为1，此时以AB为直径的圆方程为(x-2)2+(y+1)2= 8，过点(0,1)和(0,-3).所以以AB为直径的圆经过y轴上的两个定点(0,1)和(0,-3).下面证明之.

设D(0,1)，同证法一，可得故所以以AB为直径的圆经过y轴上的定点(0,1).

设Q(0,-3)，则故故以AB为直径的圆经过y轴上的定点(0,-3).

综上，以AB为直径的圆经过y轴上的两个定点(0,1)和(0,-3).

评析通过上述分析，不难发现第二问是典型的证明定点问题.第一种方法采用假设存在验证法，先假设存在定点，然后建立等量关系，若能求出相应的量，就说明存在，否则就不存在.此种方法是常用的方法.第二种方法是将相关几何量用曲线系里的参变量表示，再证明结论与特定状态或与参数无关.第三种方法是把相关变元特殊化，在特例中求出定点，再证明符合题意.

二、性质研究

本题以直线和抛物线为载体，考查求抛物线的方程，准线以及证明圆过定点.第二问突出了对圆锥曲线中定点问题的考查，是热点问题，有一定的探究意义，能够考查学生的推理能力和数学运算能力，既体现了数学本质，彰显了对数学核心素养的考查要求，又让人感受到了命题者的独具匠心.下面重点研究第二问的相关性质．

性质1如图2，已知抛物线C:x2=-2py，设O为原点，过抛物线C的焦点F作斜率不为0 的直线l交抛物线C于两点M,N，直线分别交直线OM,ON于点A和点B.则以AB为直径的圆经过y轴上的两个定点这两个定点的中点是抛物线的焦点

图2

证明设M(x1,y1),N(x2,y2)，直线l方程为y=整理得x2+2pkx-p2= 0.则由直线OM,ON方程分别为得则AB的中点为

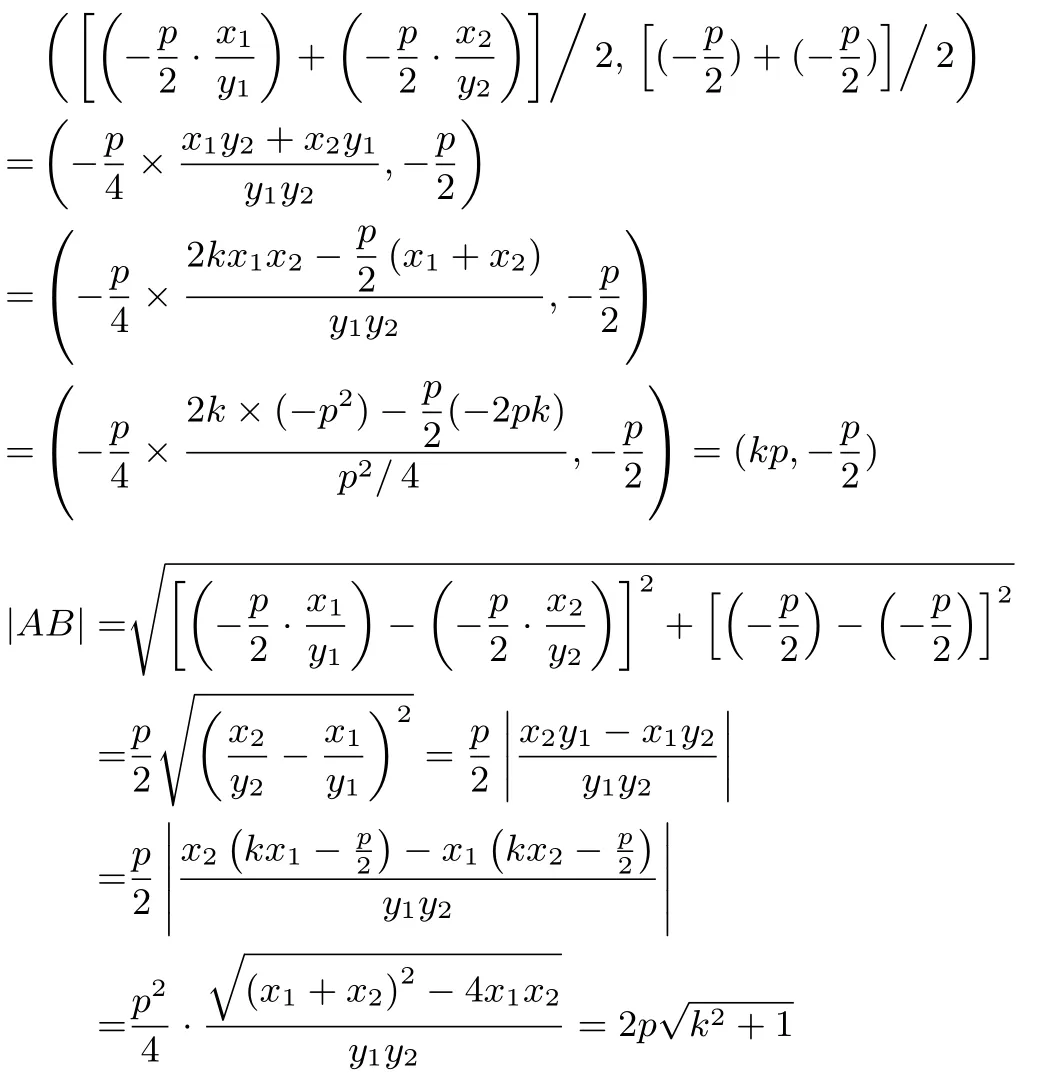
则以AB为直径的圆的半径为而且其圆心为AB的中点所以以AB为直径的圆方程为整理得由于该方程对任意0 恒成立，所以x= 0.此时则故以AB为直径的圆经过y轴上的两个定点这两个定点的中点是抛物线的焦点

同理，类似性质1 得到如下性质2，证明过程与性质1 证明类似，不再赘述.

性质2已知抛物线C:y2= 2px，设O为原点，过抛物线C的焦点F作斜率不为0 的直线l交抛物线C于两点M,N，直线分别交直线OM,ON于点A和点B.则以AB为直径的圆经过x轴上的两个定点这两个定点的中点是抛物线的焦点

三、性质推广

性质1、性质2 中的直线l都通过抛物线C的焦点，该条件可以进一步推广为l通过对称轴上任意一点，即有如下性质：

性质3 如图3，已知抛物线C:y2=2px(p ＞0)，设O为 原 点，过 点T(t,0)(t ＞0)作斜率不为0 的直线l交抛物线于点A,B，直线OA,OB分别交直线x=-t于点N和M，则以线段MN为直径的圆经过x轴上的定点和

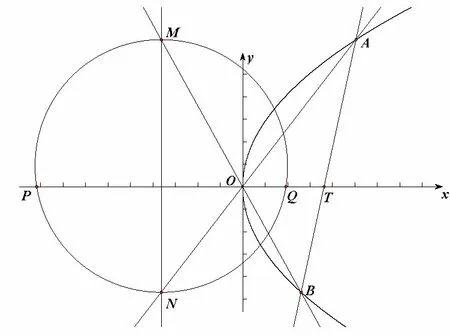
图3

证明设点A(x1,y1),B(x2,y2)，直线l的方程为x=my+t，由整理得y2-2pmy-2pt= 0.则由直线OB的方程为与直线x=-t联立方程组得到点同理可得设以线段MN为直径的圆与x轴的一个交点为P(x0,0)，则PM ⊥PN，即因为所以所以即解得：所以以线段MN为直径的圆经过x轴上的定点和

性质4如图4，已知椭圆C:1 (a ＞ b ＞0)，点R是C的左顶点，过点T(t,0)(0＜ t ＜ a)作斜率不为0 的直线l交椭圆于点A,B,直线RA,RB分别交直线于点M和N，则以线段MN为直径的圆经过x轴上的定点

图4

证明设点A(x1,y1),B(x-2,y2)，则直线l的方程为x=my+t.由整理得

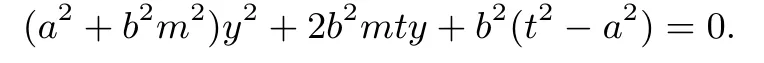
则

y1+y2=

由点R(-a,0)得直线AR的方程为y=与直线联立方程组，得到点,同理可得点当直线l的斜率不存在时，我们考虑以线段MN为直径的圆与x轴的交点.

令x1=t，则同理设以线段MN为直径的圆与x轴的一个交点为P(x0,0)，则PM ⊥ PN，即因为所以解得或所以以线段MN为直径的圆过定点

下面，我们讨论当直线l的斜率存在时，以线段MN为直径的圆也过定点和即证PM ⊥PN且QM ⊥QN.

因此

因为x1+a=my1+(t+a),x2+a=my2+(t+a)，所以，(x1+a)(x2+a)=m(t+a)(y1+y2)+m2y1y2+(t+a)2，

所以

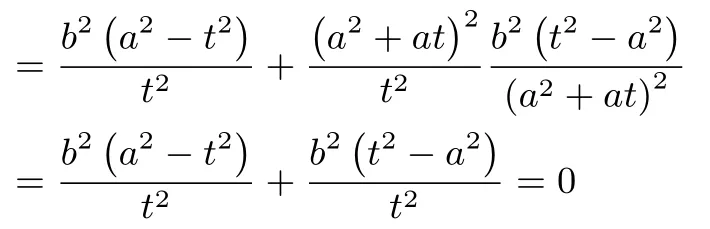
因此，以线段MN为直径的圆经过x轴上的定点和

性质5如图5，已知双曲线C:(a ＞0,b ＞0)，点R是C的左顶点，过点T(t,0)(t ＞a)作斜率不为0 的直线l交双曲线于点A,B，直线RA,RB分别交直线于点M和N，则以线段MN为直径的圆经过x轴上的定点

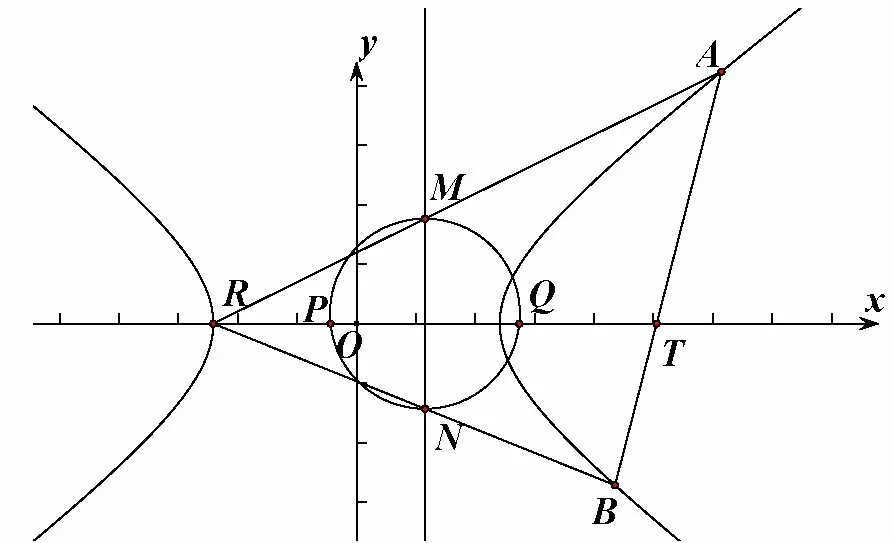
图5

证明过程与椭圆类似，不再赘述.

四、真题回顾

由以上性质不难发现，在2010年高考四川卷理科第20题，2019年福州质检理科卷第20 题，也均以上圆锥曲线的性质，体现了高考试题“常考常新，推陈出新”的理念.均可以用上述的通性通法来解答，由于篇幅关系，此处之作简析.

1.(2010年高考四川卷理科第20 题)已知定点A(-1,0),F(2,0)，定直线l:不在x轴上的动点P与点F的距离是它到直线l的距离的2 倍.设点P的轨迹为E，过点F的直线交E于B,C两点，直线AB,AC分别交l于点M,N.

(Ⅰ)求E的方程;

(Ⅱ)试判断以线段MN为直径的圆是否过点F，并说明理由.

简析(Ⅰ)E的方程为

(Ⅱ)由性质5 易得以线段MN为直径的圆过点F.

2.(2019年福州质检理科卷第20 题)椭圆E:的左焦点为F1，右焦点为F2，离心率过F1的直线交椭圆于A,B两点，且∆ABF2的周长为8.

(Ⅰ)求椭圆E的方程;

(Ⅱ)设动直线l:y=kx+m与椭圆E有且只有一个公共点P，且与直线x=4 相交于点Q.试探究：在坐标平面内是否存在定点M，使得以PQ为直径的圆恒过点M? 若存在，求出点M的坐标;若不存在，说明理由.

简析(Ⅰ)椭圆E的方程为由性质4易得以PQ为直径的圆恒过点M(1,0).

五、备考建议

1.解析几何的核心方法是用代数的方法研究几何问题.在解题过程中，首先要将文字信息、图形条件进行转换，通过代数语言描述几何要素及其关系，将已知的几何条件表示成代数式，然后进行适当的代数运算得出代数结果，最后通过分析代数结果的几何含义解决几何问题.在这个过程中要经历文字信息、图形特征和符号语言之间的多重转换，因此，我们必须重视对几何关系的深入研究，探究用何种代数形式能恰当表示题目中的几何关系，同时有利于代数运算，从而形成正确的解题策略.

2.重视解析几何的运算教学.“不会运算、运算出错”是高中数学学习的普遍现象，解析几何更是如此，很多问题学生不是不会做，只是运算能力太差，就是算不出结果或者算错，因此，教学中要利用好学生的错误运算资源，剖析失误的原因，加强“算理”的分析.

3.课堂例题要少而精.选择少而精的例题能给学生充分的探究思考的时间与空间，教师可通过探究、变式、一题多解等手段，来加强学生思维的连续性，从而调动学生的学习积极性.这就需要我们教师在选题上下功夫，在例题的解题教学分析上下功夫，找准课堂的主攻方向，是通过问题探究激发学生的兴趣，还是通过一题多解构建思想方法，或是通过问题回顾来还原知识体系等等.

4.加强解题后反思，进一步发展思维和提升能力.圆锥曲线的定点、定值和定直线等探索性问题历来是高考命题中的一个热点，此类问题往往蕴含具有代表性、引申性的数学知识、性质.由一个问题往往能引申出多个结论.它的延伸、推广，可以呈现出丰富多彩的数学内容.因此，在平常备考时，我们要有意加强对圆锥曲线性质的推导与证明，注重对往年高考题进行适当的发散研究，可以达到深化认识、举一反三的目的，使得我们在高考中就能快速作答.另外，对于培养学生发散思维、创造性品质也有着重要的意义.