超音速负泊松比蜂窝夹层板颤振分析

袁庆文，杨翊仁

（西南交通大学力学与工程学院，成都 610031）

引 言

超材料是21世纪以来出现的一类新材料，它的概念来源于电磁学，定义为具有自然界罕见的电磁特性的新型人造材料。目前超材料的概念已经逐步渗透到多个领域，超材料的定义进一步扩展为：具有天然材料所不具备的超常物理性质的人工材料，如光学超材料、声学超材料、热力学超材料、力学超材料。超材料的关键是通过设计材料的内部结构从而人为控制材料的各种属性以获得自然界没有的新材料。负泊松比材料属于超材料中的一种，与传统的正泊松比材料相比，负泊松比材料具有一些特殊的性质，具体表现在弹性模量、切变模量、抗压痕力和能量吸收等方面［1］。研究发现，当蜂窝夹层板芯层的蜂窝单元内角为凹角时，可以产生板平面内的负泊松比效应。

国内外学者对负泊松比蜂窝夹层板的固有特性进行了研究。Scarpa和Tomlinson［2］采用一阶板理论研究了负泊松比蜂窝夹层板在柱面弯曲和简支边界条件下的固有振动。朱秀芳和张君华［3］基于三阶剪切板理论和Vonkarman大变形假设推导出了负泊松比蜂窝夹层板的振动方程并计算了不同蜂窝单元参数下的固有特性。关于超音速流下的板的颤振问题，国内外也进行了大量的研究。Dowell［4］对1970年之前的学者们开展的壁板颤振分析工作进行了全面的总结。Bismarck-Nasr等［5］对含结构阻尼的非线性壁板颤振问题进行了研究，并用摄动法得到其极限环振动解。Cheng等［6］使用有限时间域模型考虑几何非线性和气动力非线性来计算热效应下的振动特性。夏巍等［7］推导出考虑热效应的颤振有限元方程，并给出了在频域和时域求解其颤振方程的方法，计算出壁板的颤振边界并分析了温度对壁板颤振边界的影响规律。肖艳平等［8］基于Kelvin粘弹性模型，根据VonKarman大变形应变-位移关系和一阶活塞气动力理论，建立三维粘弹壁板颤振方程，分析了粘弹阻尼，面内压力及壁板几何尺寸对粘弹壁板颤振特性的影响。李映辉等［9］基于Kelvin-Voigt粘弹性本构模型、小变形理论和一阶气动力活塞理论建立了三维粘弹性夹层壁板的气动弹性颤振方程，讨论了粘弹性阻尼、来流动压和夹心层厚度对颤振特性的影响。Korosh Khorshidi和MadhdiKarimi［10］研究了热环境中功能梯度夹层板的颤振特性。然而，关于蜂窝夹层壁板颤振分析方面的文章较少。

研究表明负泊松比蜂窝板具有良好的吸能特性［11］，可用于防冲击结构中。超音速飞行器在突破音障时，承受激波冲击，负泊松比蜂窝板有利于缓解激波冲击。因此，研究具有负泊松比特性的蜂窝夹层板的颤振特性是很有必要的。基于此，本文根据Reddy三阶剪切板理论、小变形理论和一阶气动力理论，建立了三维蜂窝夹层壁板的颤振方程。考虑线性稳定性问题，使用Galerkin方法将运动方程进行离散，并使用数值方法进行求解。讨论了蜂窝单元内角，直壁长与斜壁长之比，斜壁壁厚与斜壁长之比和来流马赫数对壁板颤振特性的影响。

1 具有负泊松比特性的蜂窝夹层壁板模型及其运动方程

图1所示为矩形蜂窝夹层板的边长为a和b，板厚h，芯层厚hc。沿x方向的来流马赫数Ma，流速U。

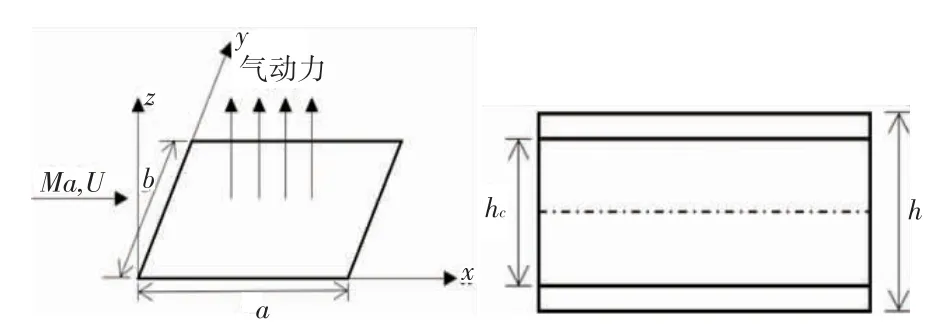
图1 蜂窝夹层板示意图

图2所示为蜂窝芯层中取出的一个蜂窝单元，用于计算蜂窝芯层的等效弹性参数。其中斜壁长L1，直壁长L2，斜壁壁厚t1，直壁壁厚t2以及内角θ，定义θ的正方向为绕x轴顺时针旋转方向。定义直壁长比斜壁长为α＝L2／L1，斜壁壁厚比斜壁长为β＝t1／L1。当蜂窝单元内角为负时，单元在受到沿x（或者y）方向远场均布荷载的作用时，将斜壁看作欧拉-伯努利梁，并考虑其伸缩变形和弯曲变形以及直壁的伸缩变形。蜂窝芯层整体表现为板平面内负泊松比现象，即沿荷载方向发生拉伸（压缩）变形，横向发生拉伸（压缩）变形。

图2 蜂窝单元示意图

式（1）中和分别为沿x方向和沿y方向的泊松比计算公式。

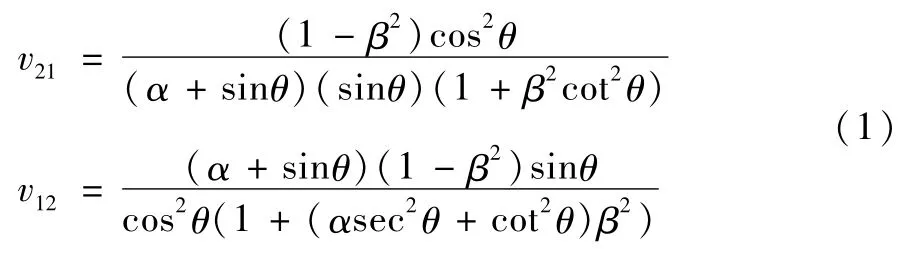
当蜂窝单元内角为负时，公式（1）计算出来的泊松比均为负。图3和图4分别表示沿x方向和沿y方向的泊松比随蜂窝单元内角的变化关系。

图3 沿x方向泊松比随单元内角变化图

图4 沿y方向的泊松比随单元内角变化图

1.1 位移场

Reddy高阶剪切变形理论［12］，选取位移场：

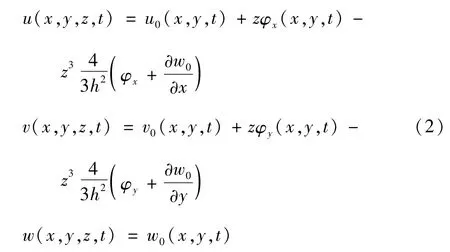
其中：u0，v0，w0分别为中面沿x，y，z方向的位移，φx和φy分别表示中面法线相对于x，y轴的转角。

1.2 几何方程

基于小变形理论，几何方程为：

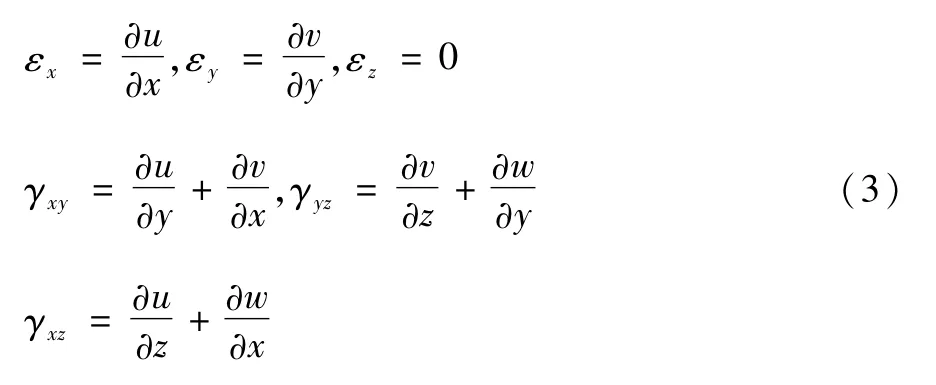
将位移场函数（2）代入几何方程（3）得到：

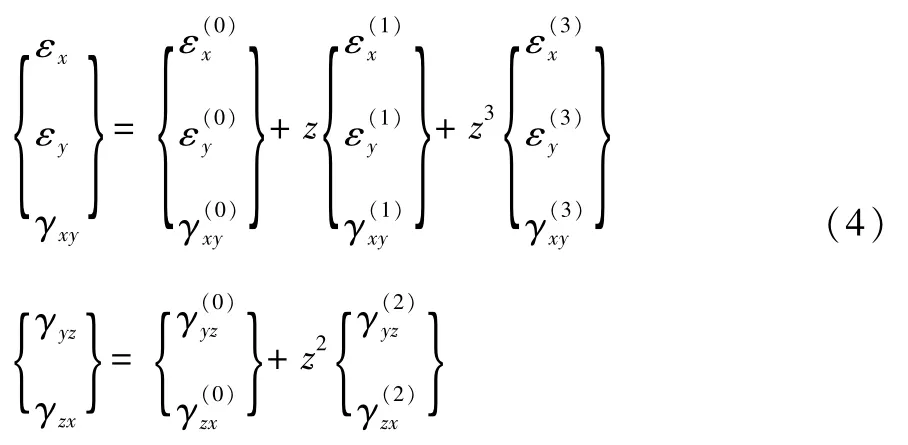
其中：

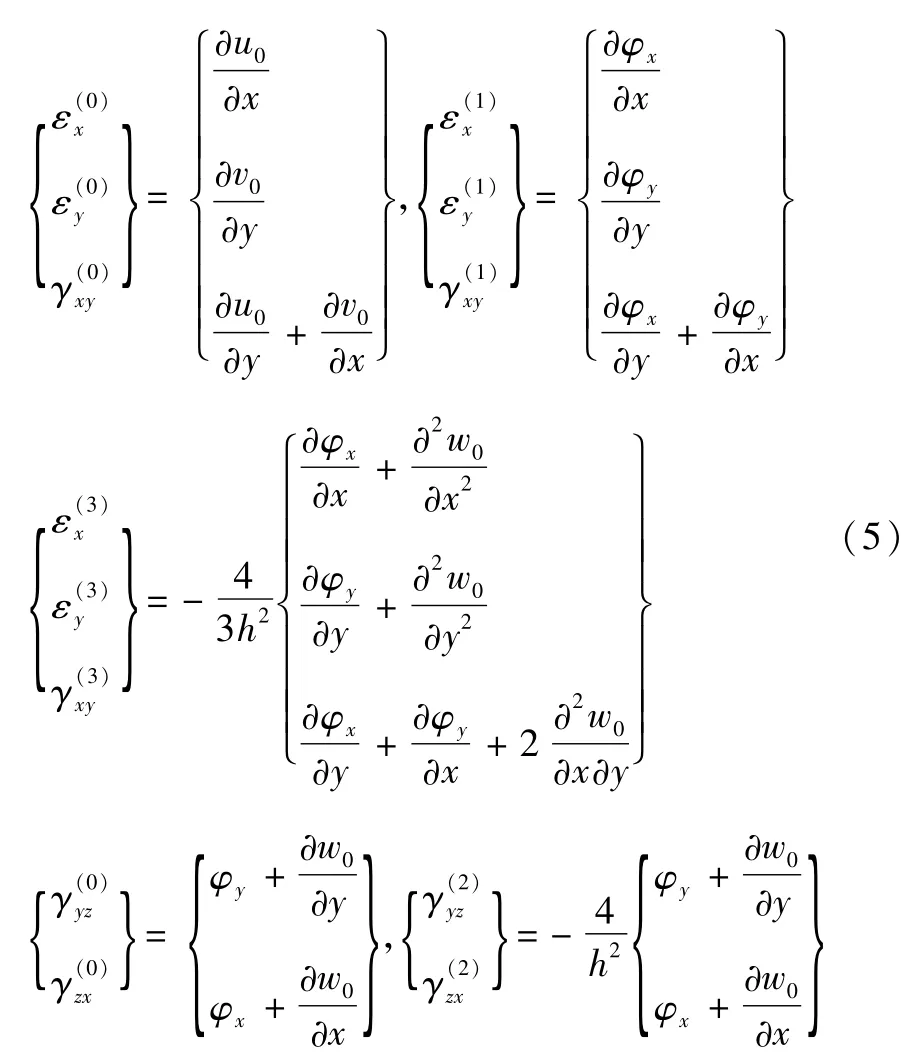
1.3 本构方程

蜂窝夹层板由3层组成，分别是上、下蒙皮层和中间的蜂窝芯层，3层的基体材料均为铝，上、下蒙皮层为各向同性材料，将蜂窝芯层看作正交各向异性材料，蜂窝芯的等效参数参考富明慧等［14］的计算公式，夹层板的本构方程为：

1.4 气动力

对于稳定性分析可以采用一阶线性活塞理论，一阶线性活塞理论的适用范围为表达式为：

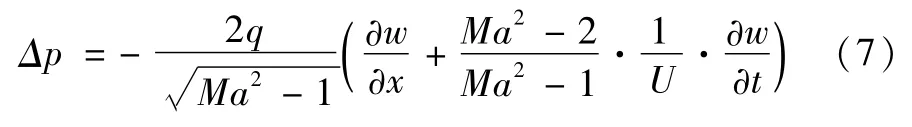
其中：Ma，ρa，U分别为来流马赫数，密度和流速，w为壁板横向振动的位移，来流速压q＝ρaU2／2。

1.5 颤振运动方程

哈密尔顿原理表达式：

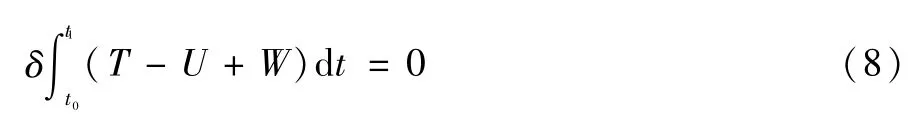
式中：T表示系统动能，U表示系统势能，W表示气动力做功。具体计算公式为：

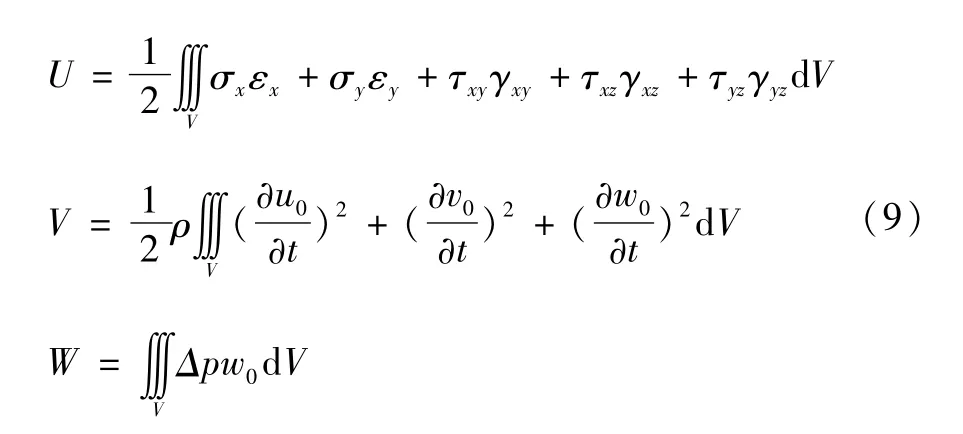
根据哈密尔顿原理即可推导出系统的线性颤振方程：

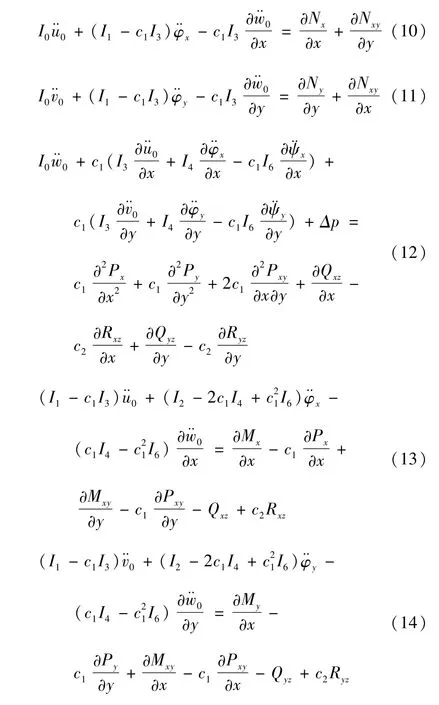
式中：

边界条件如下：

1.6 系统运动方程的伽辽金离散

板采用四边简支的边界条件。为了满足该边界条件，可假设位移表达式为：

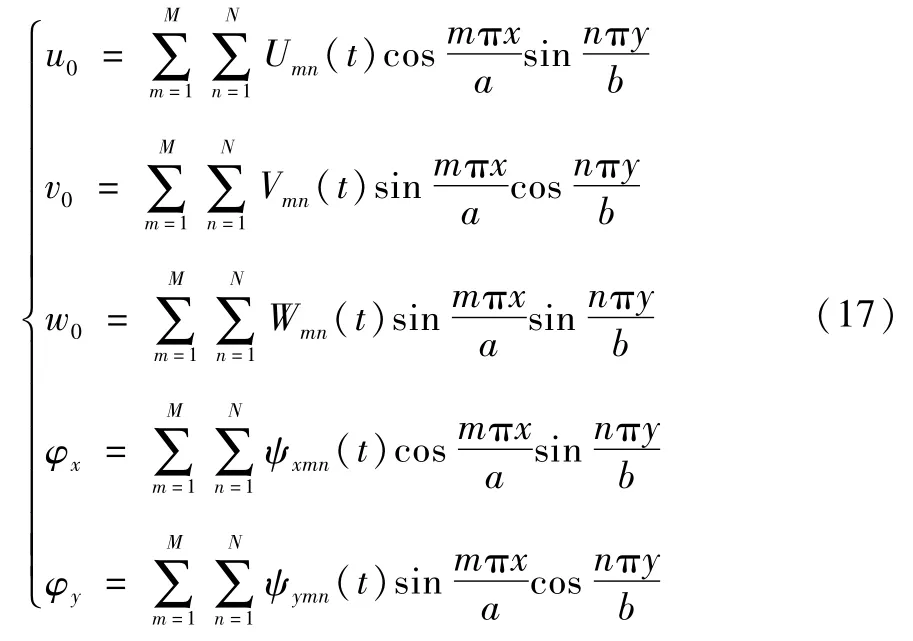
利用伽辽金离散方法，将上述位移表达式（17）代入式（10）～式（14）中，在每个方程两端同时乘以对应的三角函数并在板平面内积分，可得到离散后的常微分方程组：

其中：［M］、［C］、［K］分别为质量矩阵，阻尼矩阵，刚度矩阵，｛q｝为广义坐标列向量。将方程组降阶扩维，写成状态空间的形式。以上问题转化为式（19）特征值的问题。

计算上式特征值问题，随着来流马赫数的增加，当某一分支特征值实部为零时，系统发生颤振，此时可求出线性系统颤振时的频率和临界马赫数。

2 算例及结果分析

本文数值计算使用到的蜂窝夹层板几何参数见表1，蜂窝夹层板基体材料参数见表2。

表1 蜂窝夹层板几何参数

表2 蜂窝夹层板基体材料参数

2.1 收敛性与截断数的关系

根据文献［13］，横流向截断数N取1。图5表示顺流向截断数M分别取2，4，6，8时，一阶频率随来流马赫数增加的变化图。图5中可见，M取2时和M分别取4，6，8时的变化虽然趋势一致，但是误差较大。当M取4时，与M分别取6和8时比较仍然存在一定误差。当M取6和8时，两者计算结果基本吻合，因而认为顺流向采用6阶截断来研究蜂窝夹层板的振动特性是合理的，以下分析结果均在6阶截断下计算得到。

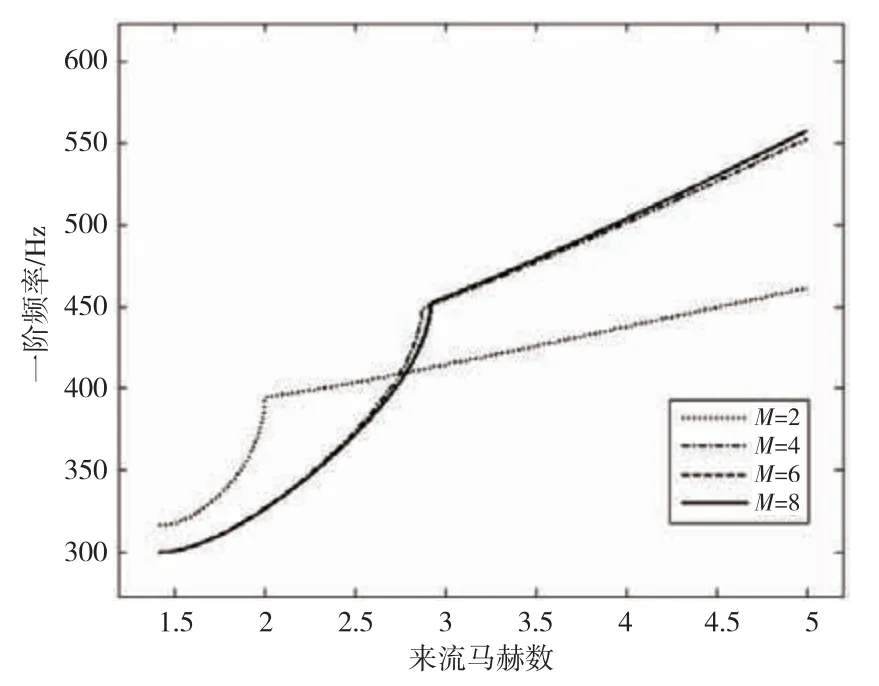
图5 截断阶数对一阶频率的影响

2.2 来流马赫数对系统特征值的影响

图6和图7分别给出了频率和特征值实部随来流马赫数的变化关系，一阶频率随来流马赫数的增大而增大，二阶频率随来流马赫数的增大而减小。当某一分支特征值实部等于零时，系统发生颤振，此时来流马赫数为临界马赫数。

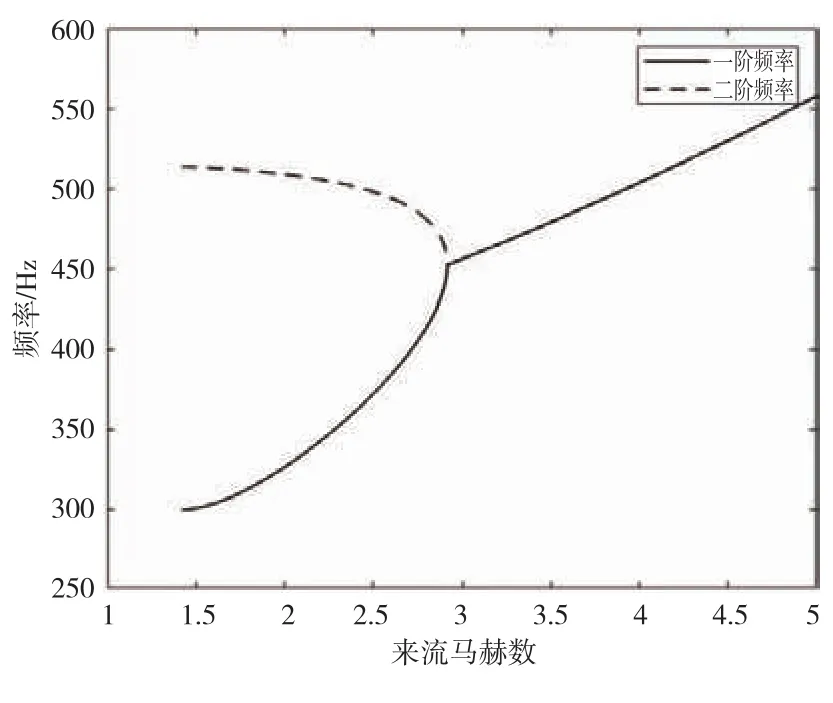
图6 频率随来流马赫数的变化图

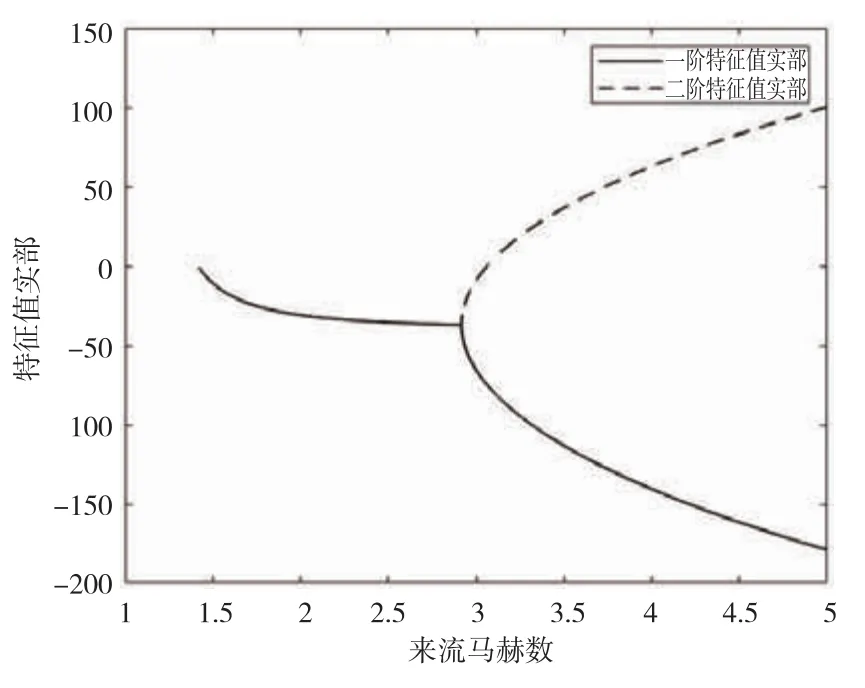
图7 特征值实部随来流马赫数的变化图

2.3 蜂窝单元参数对系统特征值的影响

图8表示颤振频率随蜂窝单元的直壁长与斜壁长的比值和单元内角的变化关系。图8中可见，单元内角增大，颤振频率先增大后减小。将单元参数β设为0.01并改变α的大小。随着α的增大，颤振频率随之增大。

图9表示临界马赫数随蜂窝单元的直壁长与斜壁长的比值和单元内角的变化关系。图9中可见，随单元内角的增大，临界马赫数先增大后减小。总体上看随内角变化，临界马赫数的大小变化不大。负泊松比蜂窝板虽然具有良好的吸能特性，但是在内角小于零时，临界马赫数并没有提高。反而在角度较小时，负泊松比蜂窝板和正泊松比蜂窝板相比临界马赫数有所下降。将单元参数β值设为0.01并改变α的大小。当内角在-80°～-50°之间时，临界马赫数随α的增大而增大。当内角大于-50°时，临界马赫数随α的增大而减小。当单元内角等于-50°时，临界马赫数对α的变化不敏感。

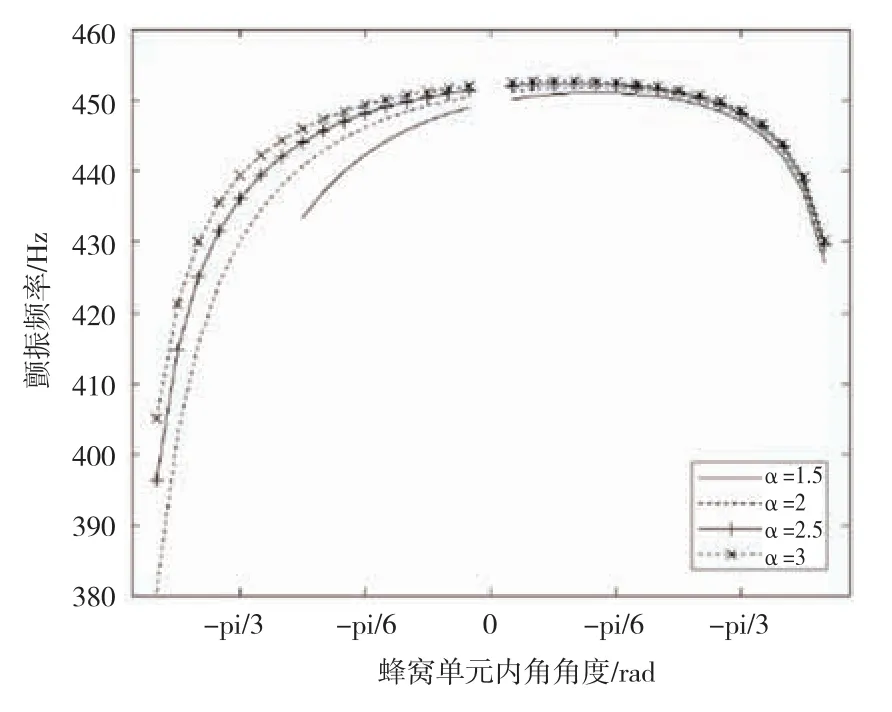
图8 颤振频率随蜂窝单元参数θ和α的变化图

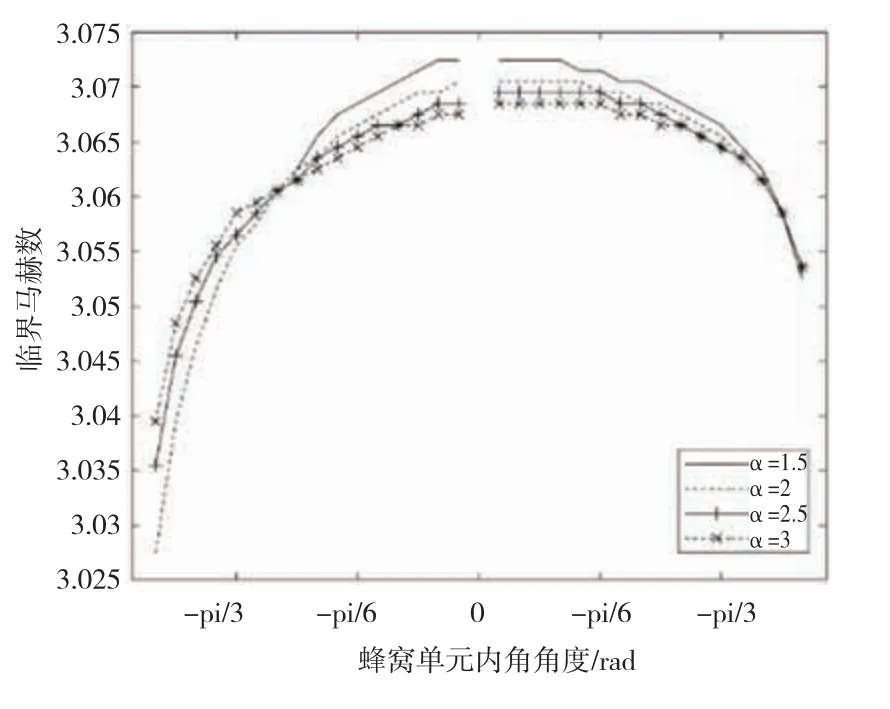
图9 临界马赫数随蜂窝单元参数θ和α的变化图

图10表示颤振频率随蜂窝单元的斜壁壁厚与斜壁长的比值和单元内角的变化关系。单元内角增大，颤振频率先增大后减小。将单元参数α设为2并改变β的大小。随β的增大，颤振频率随之减小。

图11表示临界马赫数随蜂窝单元的斜壁壁厚与斜壁长的比值和单元内角的变化关系。随单元内角的增大，临界马赫数先增大后减小。总体上看随内角变化，临界马赫数的大小变化不大。负泊松比蜂窝板虽然具有良好的吸能特性，但是在内角小于零时，临界马赫数并没有提高。反而在角度较小时，负泊松比蜂窝板和正泊松比蜂窝板相比临界马赫数有所下降。将单元参数α值设为2并改变β的大小。当内角取在-80°～-35°之间或55°～80°之间时，临界马赫数随β的增大而减小。当内角大于-35°小于55°时，临界马赫数随β的增大而增大。当单元内角等于-35°或55°时，临界马赫数对β的变化不敏感。当β较小时，蜂窝单元内角变化，临界马赫数几乎不变。

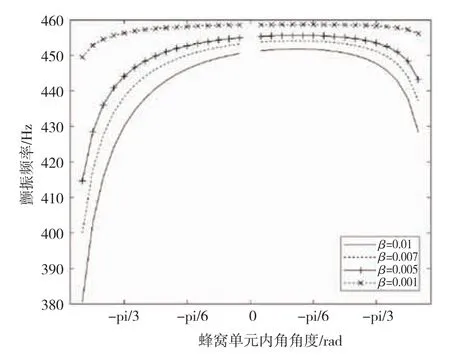
图10 颤振频率随蜂窝单元参数θ和β的变化图

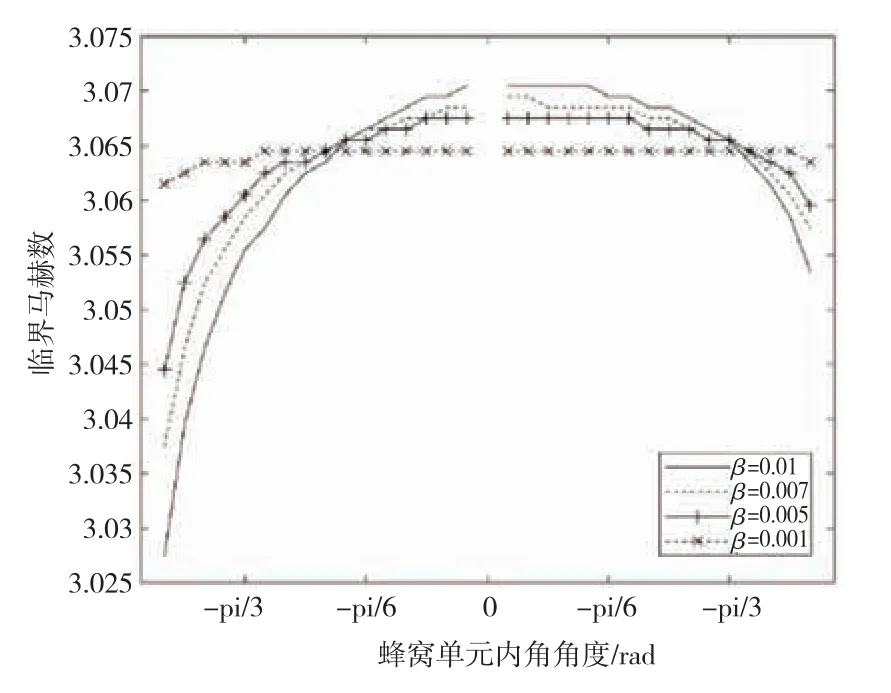
图11 临界马赫数随蜂窝单元参数θ和β的变化图

3 结 论

（1）随着单元内角的增大，临界马赫数先增大后减小。总体上看，单元内角变化对临界马赫数的影响不大。负泊松比蜂窝板虽然具有良好的吸能特性，但是在内角小于零时，临界马赫数并没有提高。与正泊松比蜂窝板夹层板相比，临界马赫数在内角较小时有所下降。

（2）随α的增大，颤振频率随之增大。当内角在-80°～-50°之间时，临界马赫数随α的增大而增大。当内角大于-50°时，临界马赫数随α的增大而减小。当单元内角等于-50°时，临界马赫数对α的变化不敏感。

（3）随β的增大，颤振频率随之减小。当内角取在-80°～-35°之间或55°～80°之间时，临界马赫数随β的增大而减小。当内角大于-35°且小于55°时，临界马赫数随β的增大而增大。当单元内角等于-35°或55°时，临界马赫数对β的变化不敏感。当β较小时，蜂窝单元内角变化，临界马赫数几乎不变。可以通过改变蜂窝单元内角、直壁长与斜壁长的比值和斜壁壁厚与斜壁壁长的比值来提高板的颤振临界。