薄壁方钢管混凝土柱的抗震性能分析

李 艺，高喜安，孙新坡

（四川轻化工大学土木工程学院，四川 自贡 643000）

引 言

薄壁结构因其受力特性，在刚度和强度方面具有优秀的特性。因此薄壁钢管结构成为解决当前工程实际问题的重要组成部分。吴波［1］、闻洋［2］研究了在不同取代率下薄壁方钢管再生混凝土短柱的力学性能。徐玉野［3］通过外包薄壁钢管的方式对受火后混凝土柱的偏压性能进行了研究，发现薄壁结构对震后结构加固具有良好的受力性能。王志滨［4］对3根带肋冷弯薄壁方钢管混凝土柱进行了滞回试验研究，加劲肋有效延缓了钢管壁局部屈曲的发生。李斌［5］、闻洋［6］在实验的基础上对薄壁钢管混凝土进行了轴压力学性能研究，对含钢率和混凝土强度等级进行了参数分析，并给出了简化的承载力计算方法。

已有的薄壁钢管混凝土柱研究多数基于试验条件下的力学性能［7-10］，而在较大轴压比作用下的抗震性能研究较少。对常用的薄壁钢管混凝土大多趋于高强混凝土方面的研究［11］，而高强混凝土的制备复杂。因此，本文在已有试验的基础上，对高轴压比的薄壁方钢管混凝土和较低标号混凝土构件进行分析，研究其抗震性能的各项指标。

1 三维数值模型

1.1 数值建模方法

本文混凝土和钢管有限元模型采用C3D8R实体单元，能够较好地模拟混凝土在低周往复荷载下的刚度退化特性［12-14］，表1列出了混凝土材料性能。

混凝土采用混凝土损伤塑性模型［13］。塑性损伤模型基于五个塑性参数和两组基本的单轴混凝土数据，五个参数分别为φ、e、σbo／σco、Kc和μ，它们定义了屈服面函数、材料的潜在流动趋势和粘滞性能［9］。单轴混凝土本构关系是其拉伸和压缩的应力-应变行为，通过定义损伤降低了混凝土构件在低周反复荷载作用下的刚度。为了确定混凝土材料，定义了包括弹性模量、泊松比和塑性损伤模型的塑性参数，表2总结了ABAQUS中塑性损伤模型所需的基本塑性参数。本文薄壁钢管采用双线性模型。

钢材和混凝土之间采用面-面接触方式，在接触面的法向采用硬接触，当接触面张开时法向压力为0，其切向采用罚函数，其钢管内壁与混凝土的摩擦系数取值0.4，切向应力的计算公式：

式中：μ为摩擦系数，p为法向压力，p0为初始粘滞力。本文忽略混凝土的初始膨胀力，因此本文取p0＝0。

表1 材料属性

表2 塑性损失模型参数

有限元模型的加载方案与试验吻合。首先，将试件的地板采用铰约束，即采用底部加载板的中线方式限制U1，U2，U3。然后，对加载板上部施加轴向压力，达到预定轴压比后，通过位移控制的方式加载水平位移，横向位移控制的循环加载以预定的漂移率施加到梁顶部，其加载示意图如图1所示。

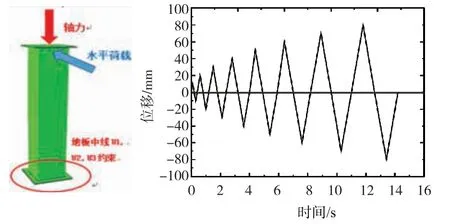
图1 加载示意图

由于薄壁钢管混凝土结构常常只研究其低轴压比的力学特性，缺少对高轴压比作用下的影响分析。此外，鉴于高强混凝土的制备困难，在工程中应用缺少普及性，本文拟对常用混凝土强度进行参数分析，研究其对薄壁钢管混凝土力学性能的影响。本文采用原试验的尺寸，具体研究内容见表3。

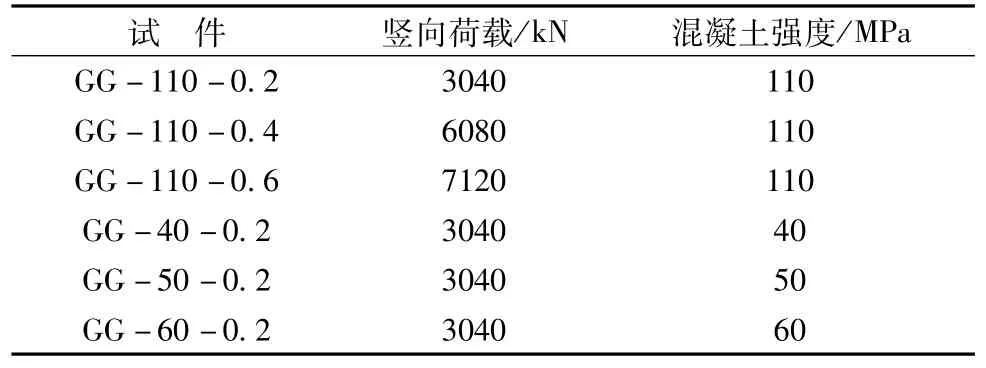
表3 钢管混凝土参数

1.2 模型验证

为了验证利用的数值模型的合理性和可靠性，对AnitH.Varma［15］开展的物理试验进行对比。试件加载过程应力变化趋势如图2所示。图2中可见，在加载初期，数值模型随着加载位移的增大，钢管底部逐渐出现塑性区，即出现应力集中现象，直至最后发生薄壁钢管的局部屈曲。

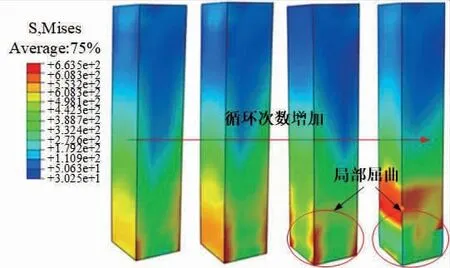
图2 试件加载过程应力变化趋势

图3（a）和图3（b）分别为试验与数值分析的荷载-位移曲线和二者的破坏模式，图中可见，数值分析与试验结果一致。综上所述，该数值模式与试验的破坏结果和荷载-位移曲线吻合良好，验证了模型的合理性和可靠性。

2 结果分析

本文在试验研究的基础上，建立了有效的有限元分析模型，以轴压比和混凝土强度为影响因子进行了参数分析，从破坏模式、荷载-位移曲线、延性和耗能四个方面研究轴压比和混凝土强度对构件受力性能的影响。

2.1 破坏模式

图4为不同试件的破坏模式，图4中可见，各个试件都是由于薄壁钢管发生了局部屈曲破坏而导致试件失去了承载力。从图4（a）可知，轴压比对试件的破坏模式影响较大，随着轴压比的不断增大，试件发生局部屈曲破坏的高度逐渐增大，并且当轴向荷载为7120KN时，出现了连续的分段屈曲的现象。从图4（b）可知，当混凝土强度较低时，试件由于局部屈曲而破坏，但是混凝土强度的变化对屈曲的高度影响不明显。

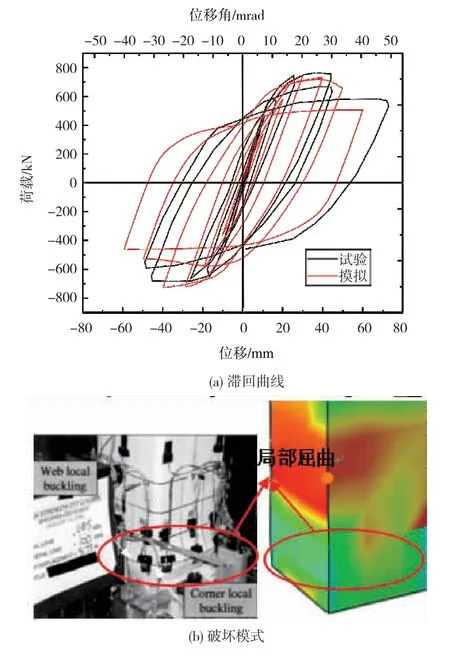
图3 结果比较

图4 不同试件的破坏模式

2.2 荷载-位移曲线

图5分别列出了不同试件的滞回曲线和骨架曲线。从图5可见，随着试件轴向荷载的不断增大，滞回曲线的饱满程度逐渐降低，且从骨架曲线可知，试件的峰值承载力和变形能力逐渐下降。此外，混凝土强度变化对构件性能的影响不明显，随着混凝土强度的提升，其极限承载力略有增加，但是其后期变形能力略有下降。

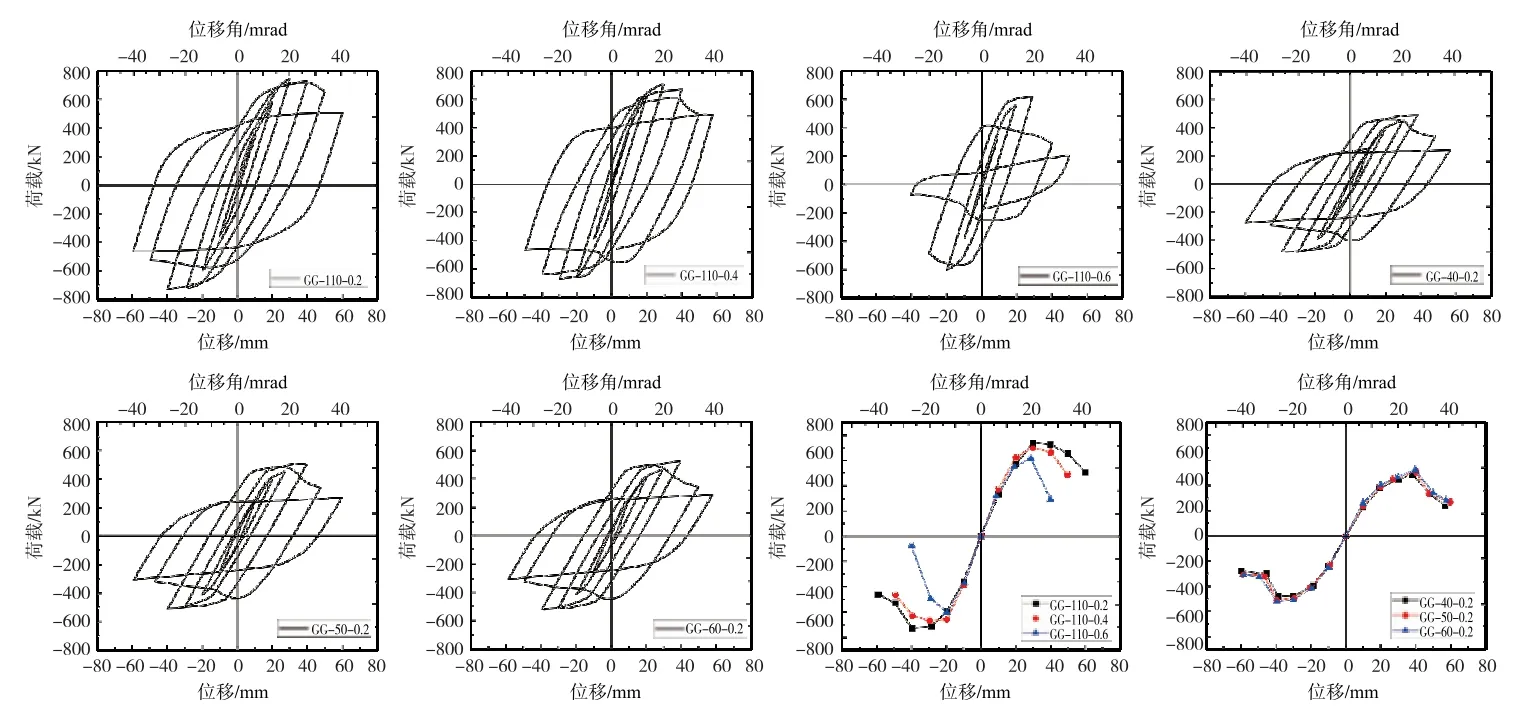
图5 不同试件的荷载-位移曲线

2.3 延性分析

根据延性所代表的变形类型，延性种类主要分为以下四类：应变延性、曲率延性、旋转延性和位移延性。对于位移延性，定义为极限状态下的位移与屈服时位移之比。延性系数计算公式如式（2）所示：

其中：Δy为试件达到屈服载荷时的水平位移值，Δμ为试件载荷值下降到最大水平力的85%或试件明显丧失承载能力时的水平位移值。表4分别列出了屈服位移值Δy、极限位移Δμ以及各个试件延性系数。

从表4可知，轴压比的变化对试件的延性影响敏感，随着轴向压力增大，其延性系数下降明显，试件GG-110-0.2的延性系数是GG-110-0.6的1.3倍。此外，混凝土强度对试件的延性影响较小，其表现的趋势为随着强度等级的增强，延性略有下降。

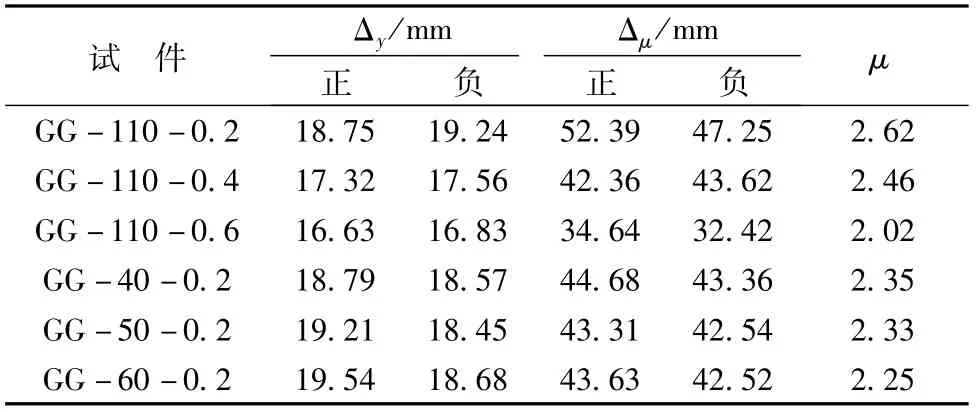
表4 各个试件的特征位移

2.4 耗能分析

耗能能力的大小是分析结构抗震能力的一个重要依据。往复作用下的耗能能力通常情况下由稳定的滞回环面积来决定。滞回面积越大，曲线越饱满，构件的耗能能力也越好。本文采用耗能E反映试件的耗能能力。

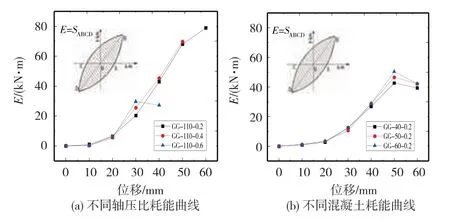
图6 试件耗能曲线

从图6（a）可见，耗能能力随着加载位移的增加逐渐增大，主要是由于试件进入塑性阶段，在往复加载中吸收了更多的变形能。试件的耗能在不同轴压比影响下，总的耗能能力明显下降，但是从加载位移的阶段而言，20mm前各个试件的耗能能力相当，当加载位移为30mm时，GG-110-0.6的耗能能力大于低轴压比试件，主要原因在于GG-110-0.6试件的水平荷载峰值阶段，而GG-110-0.4和GG-110-0.2处于较低荷载阶段。从图6（b）可见，试件的耗能能力随着混凝土强度的增加而提升，但是其增大的幅度不明显。

3 承载力计算方法研究

钢管混凝土在达到极限承载力状态时，截面的中和轴远离几何中心线，受压区域的混凝土由于高压力作用而开始膨胀，此时的钢管处于拉-压的混合受力状态，其屈服强度一般低于单向的屈服强度，根据文献［16］，其屈服强度f′y等于单向强度的0.89倍。由于钢管对混凝土的约束作用，混凝土采用约束混凝土本构模型进行计算。

图7所示为方钢管混凝土截面划分示意图，其边长分别为a和b，选取其中的一个单元体为dAs，设钢管的壁厚为t。通过划分单元，确定单元位置后，得到整个截面的轴力和弯矩，具体如式（3）和式（4）所示：

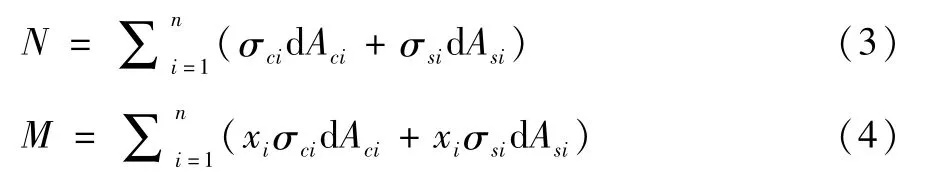
本文通过采用迭代法求取中和轴位置，当弯矩小于某一限值则可认定构件的受力状态达到极限时态，即取该时刻的xi为中和轴的实际位置。

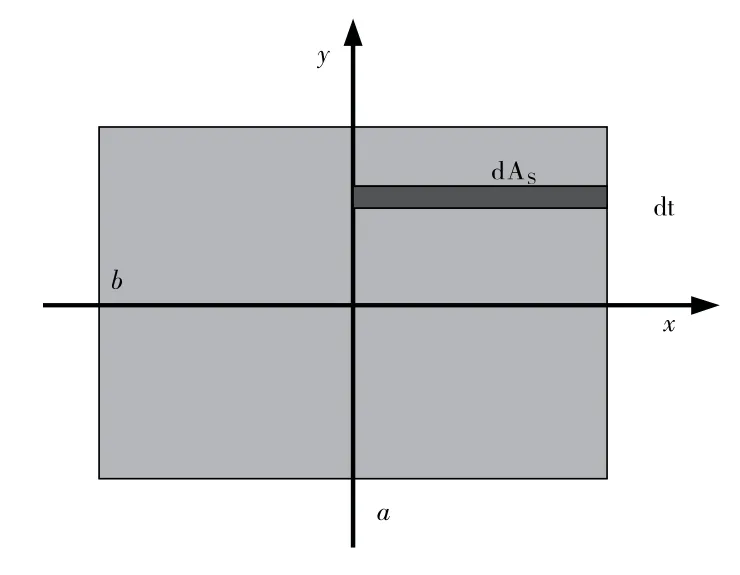
图7 方钢管混凝土截面划分示意图

文献［17］将薄壁钢管混凝土的强度同时考虑，则其组合强度为f2，受拉一侧取钢管的屈服强度f1。此处忽略了混凝土的抗拉强度，截面受力平衡示意图如图8所示，则通过截面极限平衡方程可以得到：

图8 截面受力平衡示意图

本文通过对GG-110-0.2试件进行验证分析，可得其抗弯承载力为685kN，与其实际承载力相差7.3%，验证了理论模型的可靠性。

4 结 论

通过将混凝土与薄壁钢管之间的粘结强度采用库伦摩尔模型模拟，建立了薄壁钢管混凝土的三维数值有限元模型，并且在已有试验的基础上，验证了模型的合理性。继而在试验的基础上，扩展了不同轴向荷载和不同混凝土强度对试件的力学性能的影响。结果表明：

（1）薄壁钢管混凝土试件随着轴压比的增大，其承载力和延性能力下降，且试件底部屈曲的高度逐渐增大。

（2）随着轴压比的不断增大，试件在往复荷载作用下总的耗能能力呈现下降趋势。

（3）薄壁钢管混凝土的承载力随着混凝土强度的增大而逐渐增长，其耗能能力也呈现增大趋势，但试件的延性趋于降低。

（4）通过极限平衡法提出了薄壁钢管混凝土的抗弯承载力计算方法。