大减压比高压气动比例减压阀阻尼孔耦合特性仿真研究

(华中科技大学 机械科学与工程学院FESTO气动中心， 湖北 武汉 430074)

引言

由于压缩空气清洁易于制取，且功率比重大等，高压气动技术广泛应用于航天航空、工业自动化流水线设计等领域[1-3]。陈奕泽等[4]研制了一种最高入口压力31.5 MPa，输出压力8～25 MPa的减压阀，最大减压比为4，着重研究了其流量特性及结构参数、控制器参数对系统的影响；徐志鹏等[5]研制了一种滑阀先导式高压比例减压阀，着重研究高压气动比例减压阀结冰特性对减压阀性能的影响；张春等[6]设计了一种带流量稳定器的先导式高压气动比例减压阀， 主要研究减压阀减压过程中的能量损耗问题；目前国内外研究主要集中在小减压比比例减压阀，本研究将针对一种大减压比高压气动比例减压阀进行研究。

高压气动减压阀为某装置关键部件之一，输入压力8～12 MPa，输出压力0.05～0.1 MPa，最大减压比高达240。通径为DN20，流量大，减压阀下游压力易产生超调现象。因此该比例减压阀对主阀芯开度控制精度、开启速度控制要求高，从而对该比例减压阀控制腔压力控制要求高。鉴于此，在前期结构设计的基础上建立该比例减压阀动力学模型及热力学模型，并在数学建模的基础上进行仿真研究，通过对比分析得出主阀控制腔进气阻尼孔、出气阻尼孔直径、进气阀芯开度合理耦合参数[7]，实现对该比例减压阀输出压力的稳定快速控制。

1 减压阀结构与工作原理

如图1所示为所设计减压阀结构，该减压阀由主阀、 先导阀和进气阀组成。 根据压力不同可将主阀芯分为输入腔、输出腔、反馈腔、缓冲腔和控制腔。先导阀阀芯和进气阀阀芯相关联，给定比例电磁铁一定电流，比例电磁铁产生与该电流成比例的推力，推动先导阀芯和进气阀芯下移，气体通过节流口进入控制腔；控制腔气体压力升高后打开主阀芯，阀出口有压力输出，该压力气体通过气路引导至先导阀阀芯处，在先导阀芯密封面产生推力，与比例电磁铁的推力相平衡。

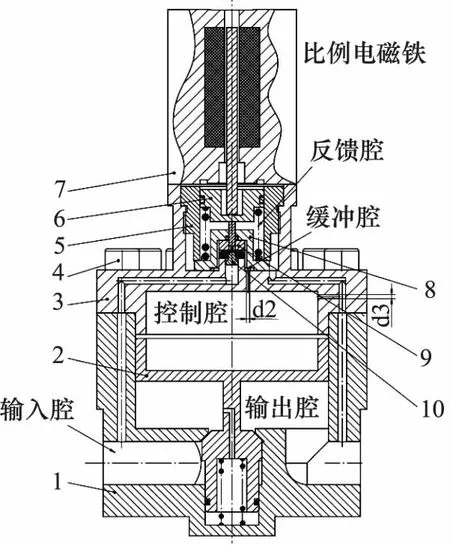
1.主阀体 2.主阀芯组件 3.先导阀体 4.螺钉 5.先导阀芯导向 6.先导阀芯 7.比例电磁铁 8.进气阀体 9.进气阀密封 10.进气阀芯 图1 比例减压阀结构示意图

当入口气体压力突然升高时，由于主阀芯开度来不及变化，下游压力也随之升高。此时，一方面，主阀芯下表面所受出口压力产生的推力会增加，使得主阀芯开口变小；另一方面，由于输出压力增加，先导腔压力随之升高，先导阀芯上移，从而导致进气阀芯开度减小，控制腔压力降低，主阀芯开度减小。综上，减压阀输入压力突然升高，主阀芯开度会减小，直到先导阀处气压力产生的推力和比例电磁铁推力产生新的平衡，从而可实现出口压力的稳定。反之可得比例减压阀上游压力突然降低时，输出压力维持稳定[8-10]。

2 比例减压阀数学模型

建立数学模型时，先做如下假设：

(1) 工作气体为理想气体，气体在各腔内及各腔之间的流动为绝热等熵流动；

(2) 不计密封比压和密封不良造成的气体泄漏；

(3) 不考虑重力对阀动力学的影响；

(4) 忽略管路中产生的气体压力损失。

(5) 先导阀芯位移大于0时，先导阀芯和进气阀芯保持接触。

2.1 阀芯动力学方程

1) 主阀芯动力学方程

主阀芯动力学方程如下：

(1)

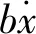
2) 先导阀芯动力学方程

先导阀芯动力学方程如下：

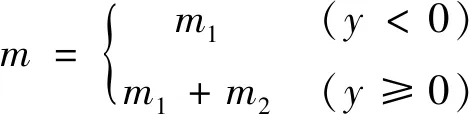
(2)

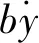
2.2 流量方程

流经阻尼孔的压缩气体质量流量方程[11-12]为：

(3)

式中,qm为流经阻尼孔的质量流量；pin为阻尼孔上游压力；Am为阻尼孔通流面积；κ=1.4为等熵指数； R=287.13 N·m/(kg·K)为气体常数；po为阻尼孔下游压力。

2.3 热力学方程

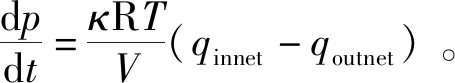
(4)

式中，Vout为输出腔体积；qout为减压阀下游用气量，其余符号意义同上。

(5)

式中，V1为输出腔体积。

(6)

式中，x0=24 mm为输出腔初始高度。

3 比例减压阀MATLAB/Simulink仿真分析

根据第2节所述数学模型建立比例减压阀的MATLAB/Simulink模型，改变控制腔进气阻尼孔直径d2和排气阻尼孔直径d3(位置见图1)并进行仿真。

针对该比例减压阀和给定进气阀芯参数，设定d2=0.2 mm，d3=1.1 mm，调定输入力为135 N，设定输入压力分别为8 MPa和12 MPa并进行仿真，可得如图2a所示比例减压阀输出压力和图2b主阀芯位移。由图可知，输入压力为12 MPa时，主阀芯开度为0.09 mm；输入压力为8 MPa时，主阀芯开度为0.14 mm，但输出压力稳态值均为0.105 MPa，因此可认为该比例减压阀可满足在不同输入压力下工作的要求。

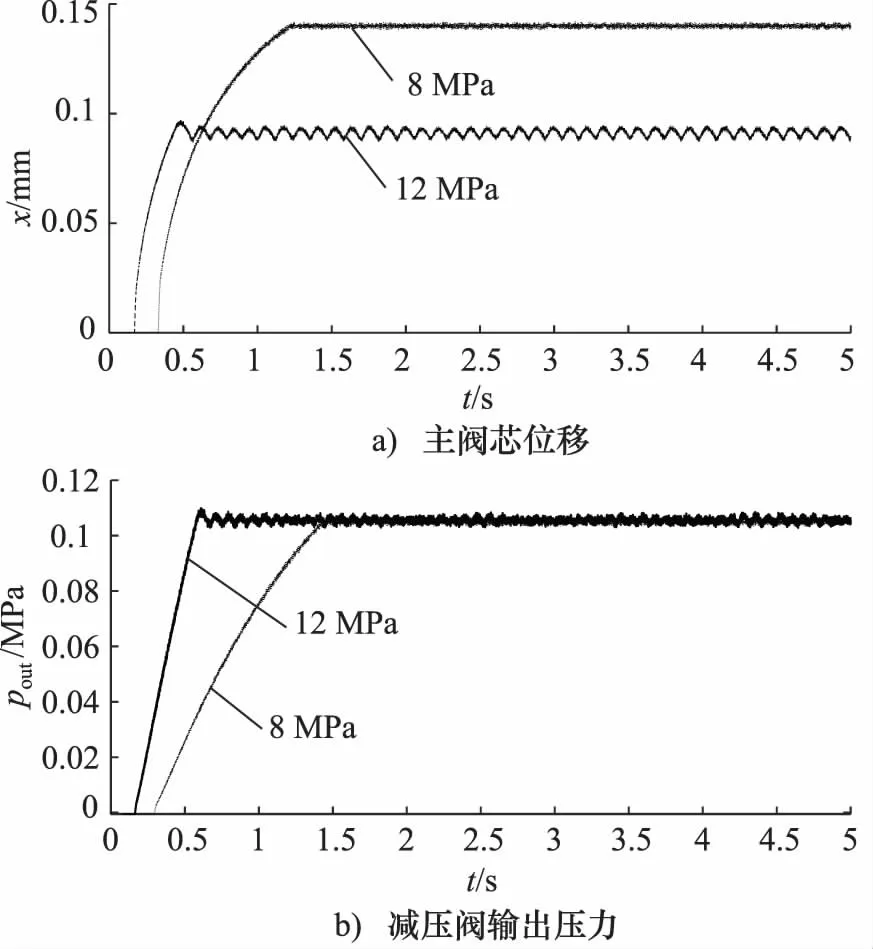
图2 输入压力分别为8 MPa和12 MPa响应曲线

如图3、图4所示，d2=0.2 mm，d3=1.1 mm，输入压力分别为12 MPa和8 MPa，比例电磁铁输入力为95， 105， 115， 125, 135 N时的输出压力阶跃响应曲线。

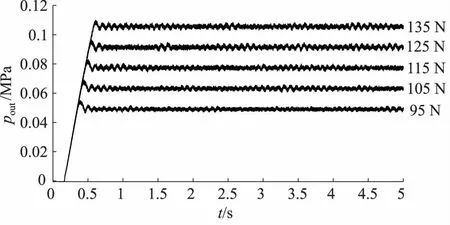
图3 输入压力12 MPa减压阀阶跃响应曲线

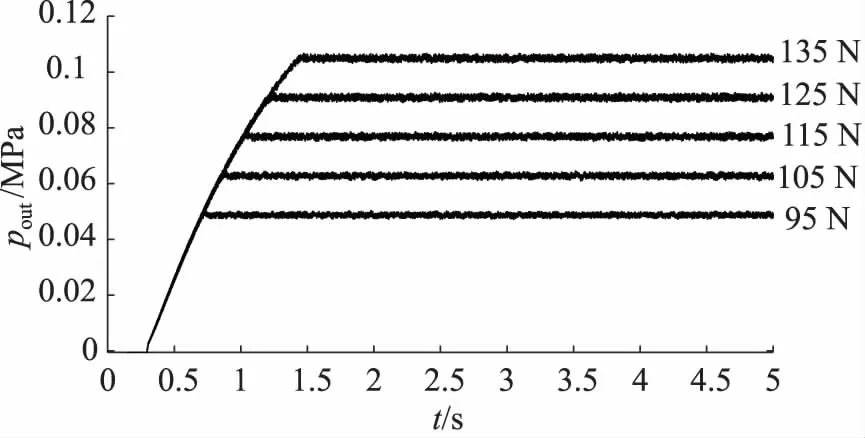
图4 输入压力8 MPa减压阀阶跃响应曲线

由图3、图4可知，输入压力发生变化，减压阀输出压力稳态值不变；输入压力较大时，输出压力响应更快，达到稳态的时间更短；且输入压力为8, 12 MPa时，输出压力均随输入压力的增加而均匀升高，即输出压力与输入压力成比例关系。

设计及仿真研究过程中，发现进气阀芯开度，与控制腔进气阻尼孔直径、控制腔出气阻尼孔直径互相耦合，直接影响控制腔压力的形成，从而影响输出压力响应。考虑到进气阀芯小顶杆强度、进气阀芯加工及进气阀芯的密封，设计进气阀芯密封面直径为1 mm。改变控制腔进、排气阻尼孔直径进行仿真，对两阻尼孔直径进行优化，得出较合理的取值。

改变孔径对于高压输出影响更大，下文考虑改变孔径对输出压力阶跃响应的影响。

如图5所示为d2=0.2 mm，d3=1.2 mm时减压阀输出压力阶跃响应曲线，由图可知，输入压力为12 MPa 时阶跃响应最大超调量有小幅减小，但输入压力为8 MPa的阶跃响应上升时间长达4 s，较为不合理。

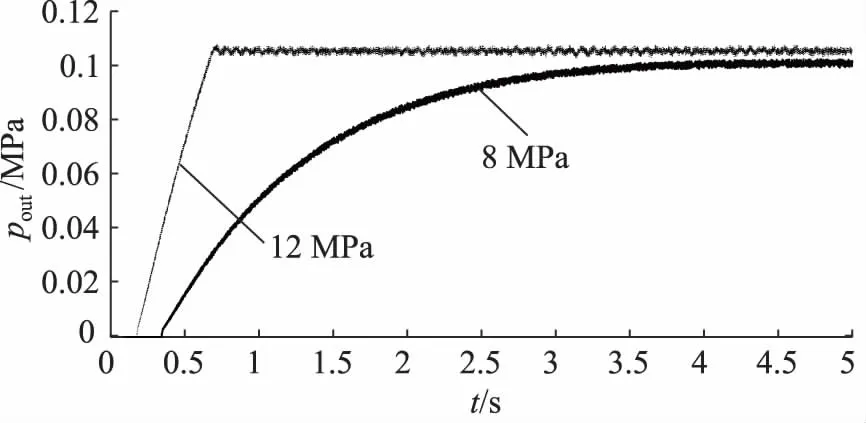
图5 d2=0.2 mm，d3=1.2 mm时减压阀输出压力阶跃响应曲线

图6所示为d2=0.2 mm，d3=0.9 mm时减压阀输出压力阶跃响应曲线，由图可知，输入压力为8 MPa时阶跃响应上升时间有所减小，但考核指标要求稳定时间小于1.5 s，且输入压力为12 MPa的阶跃响应最大超调量有所增大，不利于比例减压阀输出压力稳定性。

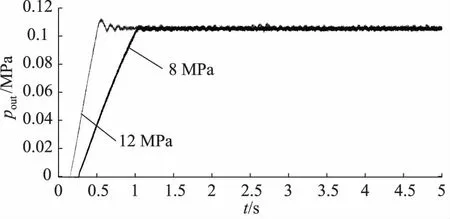
图6 d2=0.2 mm，d3=0.9 mm时减压阀输出压力阶跃响应曲线

如图7所示为d2=0.3 mm，d3=1.0 mm时减压阀输出压力阶跃响应曲线，由图可知，输入压力为12 MPa 和8 MPa时阶跃响应最大超调量均较大。

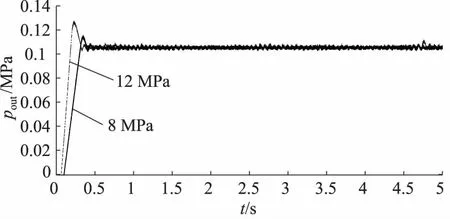
图7 d2=0.3 mm，d3=1.0 mm时减压阀输出压力阶跃响应曲线

如图8所示为d2=0.3 mm，d3=1.5 mm时减压阀输出压力阶跃响应曲线，由图可知，输入压力为8 MPa时阶跃响应超调量小，响应时间也很短，为0.7 s；但是输入压力为12 MPa时，输出压力产生较大波动，无法稳定。

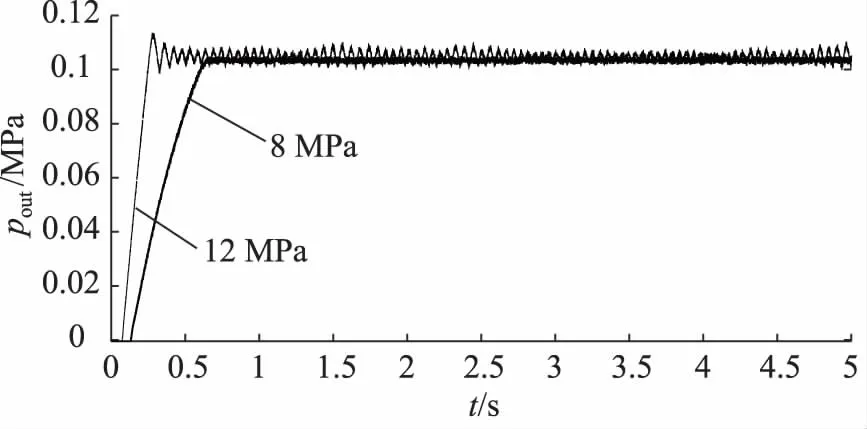
图8 d2=0.3 mm，d3=1.5 mm时减压阀输出压力阶跃响应曲线

综上可知，针对该比例减压阀和给定进气阀芯参数，设定d2=0.2 mm，d3=1.1 mm，较为适用本研究设计的比例减压阀的控制腔进、排气阻尼孔参数。增加进气阻尼孔直径，则输入压力为12 MPa时的阶跃响应易产生很大超调，这是由于进气阻尼孔直径增加时，高压气体经过阻尼孔时的减压作用降低，从而使得控制腔压力升高过快，导致超调量增加，甚至造成临界稳定状态，无法对压力产生有效控制；而继续增加排气阻尼孔直径，则输入压力为8 MPa时，由于排气阻尼孔直径增加，控制腔气压最大值会有所降低，主阀芯最大开度会减小，则可能导致输出最大压力小于0.1 MPa。

为验证该猜想，进行如图9所示的对比试验，其参数为d2=0.3 mm，d3=1.7 mm，输入压力8 MPa及d2=0.4 mm，d3=1.5 mm，输入压力12 MPa时的阶跃响应曲线。

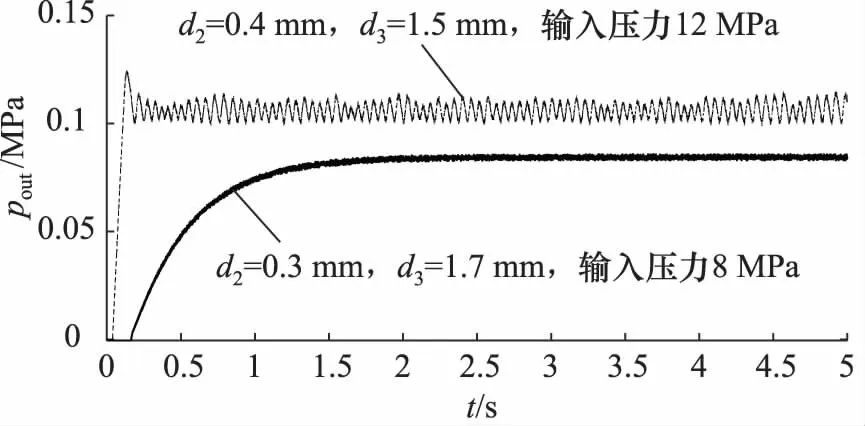
图9 不同阻尼孔直径阶跃响应

由图8及图9可知，继续增加排气阻尼孔直径，输入压力为8 MPa时，输出压力将不能达到要求，而继续增加进气阻尼孔直径会导致输入压力为12 MPa时输出压力波动很大，与分析的结果相一致。

4 结论

(1) 本研究设计了一种大减压比比例减压阀，针对大流量大减压比比例减压阀输出压力稳定控制难度大的问题，采用先导阀芯与进气阀芯联动控制控制腔压力，从而控制主阀芯开度，最终达到输出压力与比例电磁铁推力平衡，得到稳定的输出压力;

(2) 针对主阀芯控制腔进气、排气阻尼孔直径及进气阀芯开度耦合特性建立比例减压阀动力学及热力学数学模型，在数学模型的基础上搭建了MATLAB/Simulink仿真模型，并基于该Simulink模型对比例减压阀的耦合特性进行仿真，研究阻尼孔耦合特性对输出压力阶跃响应的影响，通过对比仿真得出较为合理的耦合阻尼孔参数为d2=0.2 mm，d3=0.9 mm；

(3) 通过对仿真结果的分析，得出了耦合参数变化对输出压力的精确度及稳定性的影响规律，预测孔径继续变化给输出压力带来的影响并进行仿真验证，得到的验证性仿真结果与预测相一致；

(4) 本研究对高压气动比例减压阀的优化设计及控制性能的改善提供一定参考。