全尺寸风机叶片疲劳测试技术与弯矩匹配方法研究进展综述
2020-02-18
(同济大学 机械与能源工程学院, 上海 200092)
引言
截至2018年底,全球风机累计装机容量已达642.3 GW[1]。风机叶片在20~25年的服役期间内承受上亿次具有不同载荷比的包括气动力、惯性力等在内的各种载荷,极有可能发生疲劳破坏[2]。2016年,西班牙科鲁尼亚省北部的Corme风电场内某风机上15 m长的叶片断裂并撞击了280 m外的房屋[3]。2017年,位于美国俄克拉荷马州伊尼德市东部10英里的一架风机发生故障,其叶片从机身脱落,机身后面100码(约91.44 m)内的玉米田地遭受严重破坏[3]。随着累计装机数量增加,叶片故障事件数量也逐年增加,从2005年的全年12件增至2018年的全年27件[4]。为了避免因叶片疲劳破坏造成经济损失,国际电工委员会以及挪威船级社分别提出疲劳测试标准IEC 61400-23[5]、DNV-GL-2015[6],指出叶片装机前必须进行疲劳测试。
1 疲劳测试原理与弯矩匹配方法
以共振型疲劳测试为例,其测试结构如图1所示,叶片通过法兰和螺栓固定于基座上,并通过夹具将激振器固定在叶片上。
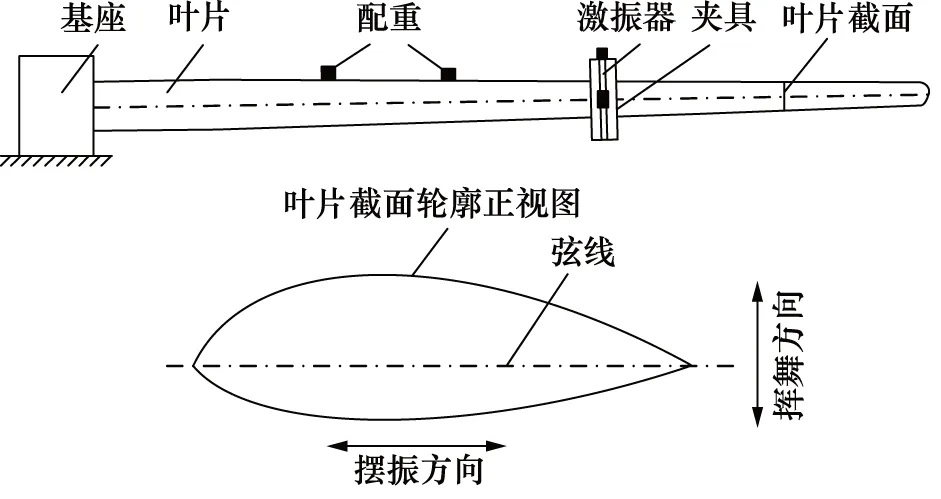
图1 疲劳测试结构示意图
如图1所示,疲劳测试按照测试方向分为挥舞疲劳测试和摆振疲劳测试。如图2所示,以挥舞疲劳测试为例,测试时,施力装置提供外力F(t),单个周期内叶片在F(t)的作用下先后经历平衡位置、极限位置a、平衡位置、极限位置b、平衡位置,叶片材料也随之在拉伸和压缩状态间反复转换,从而产生损伤。
如图2所示,测试前若仅在叶片上安装激振器而不进行弯矩匹配,叶片各截面测试弯矩与目标弯矩间通常误差很大,造成由疲劳测试测得的叶片实际疲劳寿命可信度降低。为了提高测试结果的可信度,疲劳测试前通过弯矩匹配使弯矩误差处于限定范围内,譬如相对弯矩误差小于20%[7]。故疲劳测试实际上由两部分组成:弯矩匹配与测试执行[8]。
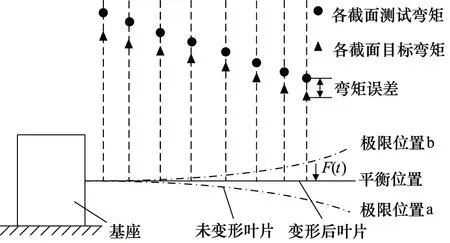
图2 结构稳定振动以及弯矩误差示意图
2 疲劳测试技术分类
疲劳测试技术按照加载方向数量分为单轴测试和双轴测试。前者主要为丹麦的叶片测试机构所采用,譬如丹麦国家可再生能源实验室(RIS∅),而诸如美国国家可再生能源实验室(National Renewable Energy Laboratory)等机构认为双轴疲劳测试中叶片同时承受两个方向上载荷更符合叶片实际运行时的受力状况。
2.1 单轴疲劳测试
1) 强制位移型
NREL设计的单轴强制位移型测试装置[9],其通过机械结构强制带动叶片位移,其中机械结构为液压加载器或凸轮与杆件[10]。采用液压加载器作为施力装置的实例如图3所示。测试时,改变液压缸进油方向使活塞杆作往复运动,通过铰链与活塞杆刚性连接的叶片随活塞杆同步运动。强制位移型测试通过改变加载力幅值和加载点个数实现弯矩匹配, 液压加载器需要较大行程来提供足够的液压力。

图3 单轴强制位移型疲劳测试装置示意图[10]
2) 共振型疲劳测试
共振型疲劳测试的核心思想是对叶片施加频率与叶片固有频率相近的力以激发叶片共振。与强制位移型疲劳测试相比,共振型疲劳测试能耗低、测试周期短,更为契合大型叶片疲劳测试需求。目前共振型疲劳测试根据激振器种类分为:旋转质量型、往复质量型以及电磁脉冲型。
(1) 旋转质量型
旋转质量型测试装置最早是由Aeroform公司设计[9]。如图4所示,测试时,电机匀速转动,偏心质量在随电机同步转动的过程中对叶片施加频率与叶片固有频率相近的简谐惯性力,激发叶片共振作上下往复运动。该方法由于偏心质量安装位置偏离夹具中心,测试时会引入不需要的的扭力,同时由于旋转半径、质量、频率固定,该方式只能进行等幅加载[12]。
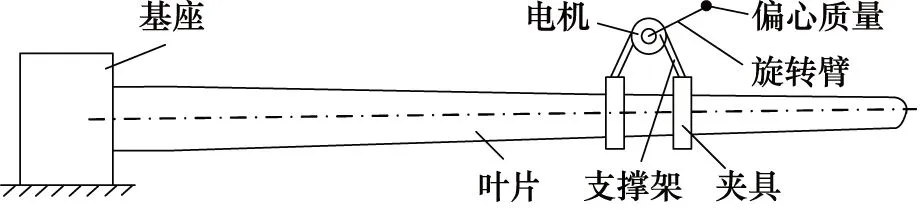
图4 共振型疲劳测试装置示意图[11]
(2) 往复质量型
往复质量型根据驱动方式分为电液伺服型和电动伺服型。采用前者的测试机构包括NREL和NaREC[9,10,13],后者由PAN等人设计[12]。
电液伺服型装置如图5所示,激振质量安装在液压加载器末端,而液压缸通过支撑架固定于叶片夹具上。电机伺服型装置如图6所示,激振质量安装于可沿丝杠移动的平台上,丝杠与电机同样通过支撑架安装于固定在叶片的夹具上。测试时,两测试装置分别通过液压加载器、电机驱动滚珠丝杠来驱动激振质量,且分别通过改变液压加载器内进油方向、电机旋转方向来改变激振质量运动方向。与旋转质量型一样,测试时,往复质量型测试装置中的激振质量产生频率与叶片固有频率相近的简谐惯性力激发叶片共振,但相比于旋转质量型, 由于往复质量型装置的质心位于夹具中心,所以测试时不会引入额外扭转力[12],且能够实现等幅加载和变幅加载。
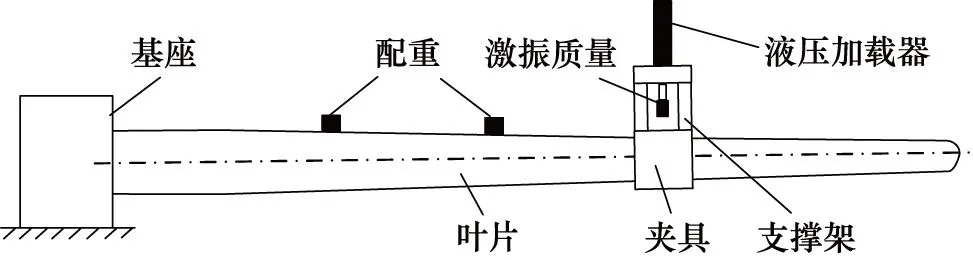
图5 电液伺服型疲劳测试装置示意图[9]
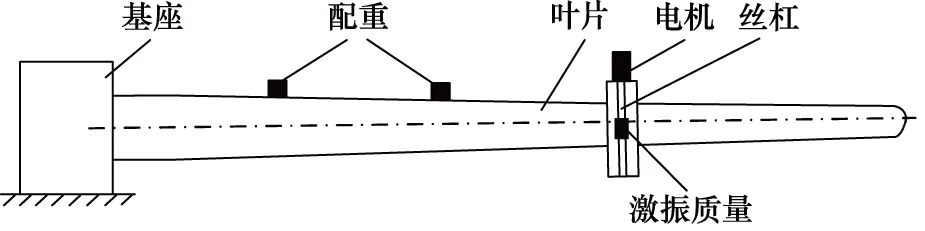
图6 电动伺服型疲劳测试装置示意图[12]
(3) 电磁脉冲型
如图7所示,电磁脉冲型加载装置主要由夹具、铁芯、线圈等组成,通过控制线圈通断电使叶片上下往复运动。线圈通电时产生磁场吸引铁芯向下运动,当叶片到达指定位置,线圈断电,磁场消失,叶片在自身弹性力作用下向上运动。通过控制通断电频率使施加在叶片上力的频率与叶片固有频率相近,从而激发叶片共振。
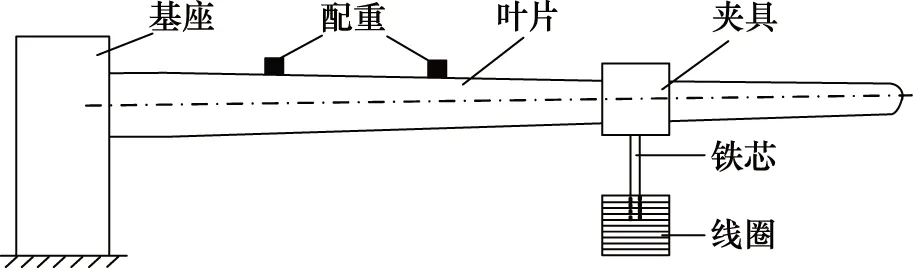
图7 电磁脉冲型加载装置示意图
2.2 双轴疲劳测试
与单轴疲劳测试类似,双轴疲劳测试根据加载方式分为强制位移型、共振型以及混合型。
1) 强制位移型
在Aeroform公司设计出旋转型疲劳测试装置后,荷兰、美国也先后开展了相关研究。荷兰代尔夫特理工大学(Delft University of Technology)的VAN D R V等[15]于1986年开发了如图8所示的双轴强制位移型疲劳测试装置,历时9个月完成30 m铁质风机叶片的疲劳测试。该装置与单轴强制位移型疲劳测试装置相同点在于加载原理相同,区别在于前者采用两个液压加载器,而后者仅用一个。
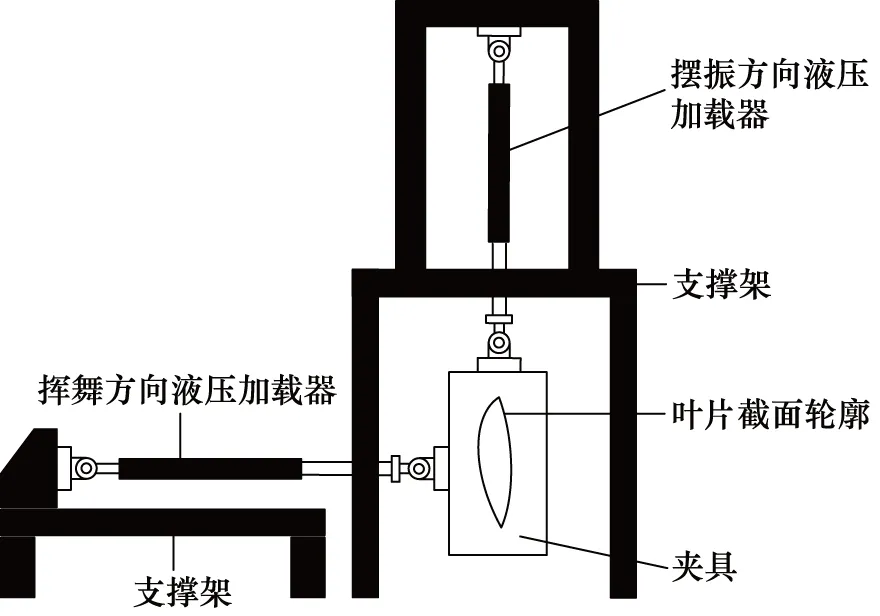
图8 双轴强制位移型疲劳测试加载装置示意图[10]
之后,NREL的HUGHES S D以及MUSIAL W D于1999年开发出新型双轴强制位移型疲劳测试装置[2]。如图9所示,摆振方向液压加载器垂直放置,并通过摇臂和推杆将该液压加载器产生的垂直力转化为水平力。
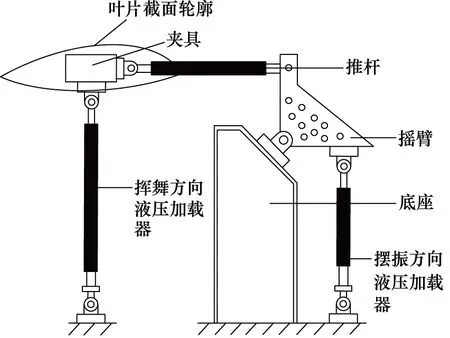
图9 改进后双轴强制位移型疲劳测试装置示意图[2]
2) 混合型
考虑到强制位移型加载方式成本高、耗时长,NREL于2004年提出混合型疲劳测试方式[16],其中,挥舞方向和摆振方向分别采用共振型和强制位移型加载方式,如图10所示。
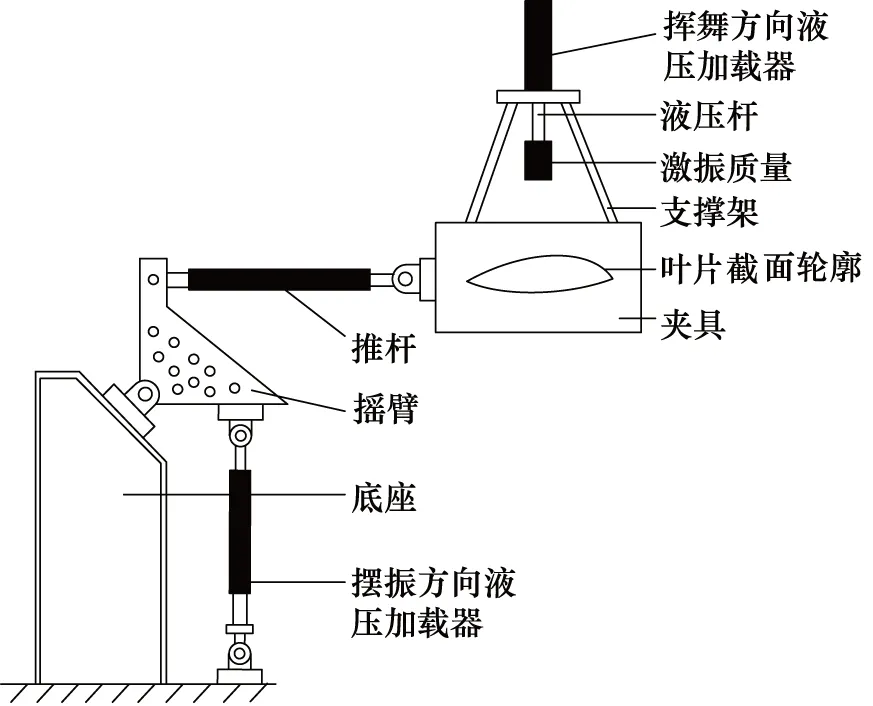
图10 双轴混合型疲劳测试装置示意图[16]
该方法与双轴强制位移型疲劳测试相比,消耗的能量和时间分别降低了65%,50%,且设备以及操作成本更低[16]。但随着叶片尺寸增大,测试中挥舞方向叶片位移增大,使得摆振方向液压加载器行程随之增大,测试成本增加。此外,为使摆振方向测试弯矩接近目标弯矩,需要多个摆振方向液压加载器,进一步增加测试成本[17]。
3) 共振型
为了降低测试成本,各机构分别开发不同的双轴共振型疲劳测试系统。英国国家可再生能源中心(National Renewable Energy Centre)开发的名为紧凑共振质量系统(Compact Resonant Mass system)的双轴共振型疲劳测试系统[18],并在长40 m的叶片上完成测试。图11为NREL开发的惯性共振激振器(Inertial Resonant Exciter),并于2014年在截断后长为45.5 m(原长49.7 m)的叶片上完成双轴测试[19],其中挥舞方向激振器与摆振方向激振器安装位置不同。测试时,通过改变液压缸进油方向驱动固定于活塞杆上的激振质量往复运动,激振质量产生频率与叶片固有频率相近的激振力激发叶片共振。
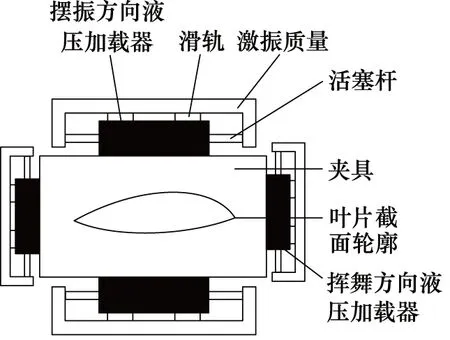
图11 惯性共振激励系统示意图[19]
3 弯矩匹配理论发展
3.1 目标弯矩设计过程
理想情况下,疲劳测试中施加在叶片上的载荷应与叶片实际服役期间承受的载荷完全一致,才能保证对叶片造成的测试损伤与叶片实际损伤完全相同。但叶片服役期间的载荷谱通常包含超过上亿次不同载荷比的载荷循环,完成数量如此庞大的载荷循环测试需要耗费巨量时间[2]。为了缩短时间,疲劳测试执行前测试机构通过以下步骤减少载荷循环次数[9]:
(1) 根据国际标准采用仿真软件模拟获取实际载荷谱;
(2) 根据载荷谱对叶片截面进行梁应变分析;
(3) 采用雨流计数法统计应变时间历程并将其代入Palmgren-Miner线性损伤公式求得实际损伤;
(4) 根据等效损伤原理,将实际损伤转化为百万次由目标弯矩定义的恒幅恒频载荷。疲劳测试通过施加恒幅恒频载荷使叶片振动百万次,且在振动过程中保证叶片上测试弯矩与目标弯矩相等,即可使叶片产生与实际损伤等效的测试损伤,从而检验叶片实际寿命是否满足设计要求。
3.2 弯矩匹配方法
以往叶片尺寸小,强制型疲劳测试通过改变施加力的幅值和施力装置的数量进行弯矩匹配。但随着叶片尺寸逐渐增大,凭借成本低、测试周期短等优点,共振型疲劳测试已成为主流加载方式,故时下弯矩匹配的研究对象多为共振型疲劳测试。
共振型疲劳测试主要通过在叶片上安装配重降低系统固有频率以降低叶片质量产生的非线性弯矩并引入配重质量产生的线性弯矩,从而调节截面上的弯矩分布,降低弯矩误差。该方式的重点与难点在于配重数量、位置和质量的选取,若数量、位置和质量选取不合理,不仅会扩大弯矩误差,还会增加不必要的能量损耗。包括激振器上的配重在内,叶片配重数量通常为2~4个,激振器数量通常为1~2个[7,9,12,20]。目前获得计算弯矩的方法主要包括有限元法和传递矩阵法(Transfer Matrix Mehood,简称TMM)。其中有限元法采用的有限元模型包括壳模型和梁模型。
1) 有限元法
(1) 壳模型
采用壳模型作为结构分析对象的方法由NREL提出[21],并得到广泛应用[22-25],其中ZHANG等将其应用于弯矩匹配领域。ZHANG[7]采用叶片壳模型作为有限元分析对象,相比于仅用单个节点描述截面的梁模型,壳模型采用足够多的节点来描述叶片截面形状,可以更精准地模拟叶片实际振动方向。在此基础上,ZHANG以配重位置和质量、激振器位置和质量、叶根弯矩幅值以及叶片截断长度作为优化变量,以叶片各关键截面上目标弯矩相对误差平方和为目标函数,通过如图12所示的粒子群算法获得使关键截面弯矩误差最小的配重位置和大小方案。
粒子群算法具体如下:
① 利用MATLAB程序在变量域内随机生成若干个变量方案,也称粒子;
② ANSYS读取粒子信息,并计算粒子对应的叶片测试弯矩;
③ MATLAB读取测试弯矩,计算并判断各粒子相对弯矩误差是否在预设范围内,若满足,计算并比较各粒子的目标函数值,也称适应值,记录各粒子和所有粒子的适应值的最小值以及对应的粒子信息,若不满足,则根据公式(1)更新粒子信息并从第2步迭代;
④ 判断迭代次数是否满足要求,若满足要求,则输出所有粒子目标函数值最小值对应的粒子信息,否则根据公式(1)更新粒子信息并继续从第2步迭代。
根据该方法,ZHANG对38 m叶片进行弯矩匹配,结果显示在0~20 m叶片范围内弯矩误差基本小于5%,匹配效果良好。
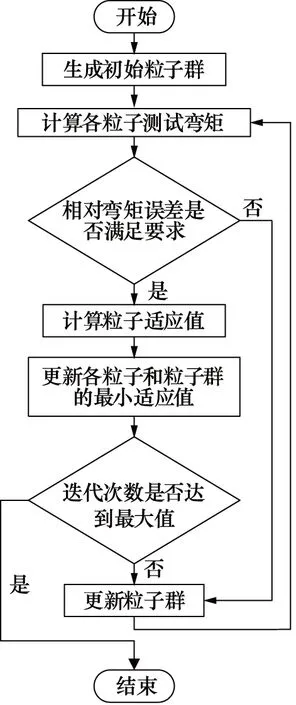
图12 优化流程图[7]
(2) 梁模型
壳模型虽然能够准确表达出叶片振动方向,但结构复杂,有限元仿真计算量大,所以许多学者采用梁模型作为结构分析对象[26-29],其中LEE[8]将其应用于弯矩匹配领域。为了减少计算量,LEE将叶片简化为等截面对称梁,大大降低结构复杂度,并通过将有限元计算结果与试验数据的对比验证了梁模型的可行性,结果显示根据梁模型计算得到的测试弯矩与试验数据基本吻合。在梁模型的基础上,LEE提出分布确定配重位置和质量,首先以分线段法确定配重位置,之后在配重位置确定的条件下,通过有限元梁模型计算并比较不同配重质量方案对应的弯矩误差来获得使叶片关键截面弯矩误差最小的最优配重质量,具体流程如图13所示。
2) TMM法
TMM法是上世纪20年代建立起来用于研究弹性构件一维线性振动问题的方法。之后, 传递矩阵法凭借编程简单、计算快速等优点,在各个领域内得到了广泛应用。譬如,1943年在MYKLESTAD[30]将其用于计算飞机机翼与其他类型梁的非耦合弯曲振动固有模态。RUI等[31]于2008年在该方法的基础上对火箭发射系统位移动态响应进行分析。FEYZOLLAHZADEH等[32]于2016年将TMM运用于海上风机塔的动态分析,且计算得到的系统一阶固有频率与实验数据误差仅为1.77%。
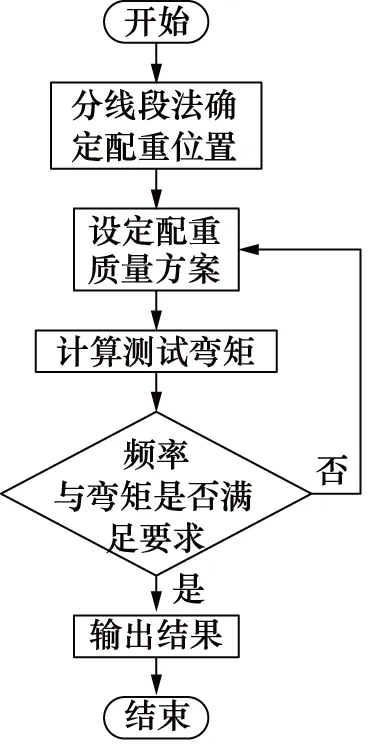
图13 生成配重方案流程图[8]
壳模型法与梁模型法,统称为有限元法,都需要利用有限元模型计算测试弯矩,采用此类方法获取配重信息需要消耗大量时间。为了减少计算时间,WU等[20]基于叶片结构类似于悬臂梁且叶片振动是典型的一维振动问题的事实将TMM用于求解叶片截面弯矩,并根据实际条件确定位置和配重质量范围,之后梯度选取多种配重质量方案,最后比较TMM计算得到的安装配重后叶片关键截面弯矩相对误差的标准差,将标准差最小的方案确定为最优配重质量。
TMM计算弯矩误差标准差过程如图14所示,具体如下:
① 根据传递矩阵法将叶片简化为有限个截面形状相同的单元,每个单元由无质量梁段和集中质量组成,如图15所示;
② 根据受力分析建立各单元左右端截面状态矢量间的传递方程,如公式(1)所示,其中状态矢量由挠度、转角、弯矩、剪力构成;
③ 将单元间的传递矩阵依次相乘获得叶根截面状态矢量与叶尖截面状态矢量间的传递方程,如公式(2)所示;
④ 根据公式(2)和公式(3)所示的叶根与叶尖之间的传递矩阵以及边界条件获得公式(4),采用二分法求解叶片一阶固有频率;
⑤ 将计算得到的固有频率以及边界条件代入公式(1)计算各截面测试弯矩;
⑥ 根据各截面测试弯矩以及目标弯矩,计算关键截面相对误差的标准差。
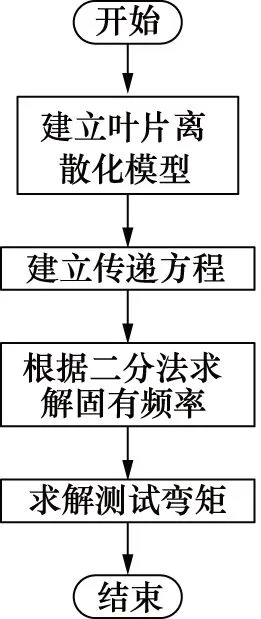
图14 TMM法中弯矩计算流程图[20]

图15 TMM叶片离散化模型[20]
单元左侧与右侧之间的传递方程:
Zri=HiZli
(1)
其中,Zli,Zri,Hi分别为单元i左右侧状态矢以及传递矩阵。
叶根与叶尖之间的传递方程:
Zt=HnHn-1,…,H1Zr=HZr
(2)
其中,Zt,Zr,H分别为叶尖状态矢量、叶尖状态矢量、以及叶根和叶尖之间的传递矩阵。
叶根与叶尖之间的传递矩阵:
(3)
其中,hij为矩阵H第i行第j列元素,i=1,2,3,4,j=1,2,3,4。
传递矩阵部分元素构成的方程:
h33h44-h34h43=0
(4)
3) 其他方法
由于通过安装配重来实现弯矩匹配会降低系统固有频率,延长测试周期,并增加结构冗余度,EDER M A等[33]提出无需安装配重的弯矩匹配方法,该方式通过改变两激振器的激振力来实现弯矩匹配,其中两激振器激振频率分别与叶片一阶、二阶固有频率相等以激发叶片不同共振模态。
3.3 弯矩测量技术
如3.2节所述,LEE对比有限元计算结果与试验数据验证梁模型的可行性,其中试验数据通常通过以下步骤获得:
(1) 在叶片关键截面处的表面安装应变计;
(2) 疲劳测试前,在叶尖施加静态点载荷,使各应变计获取相应的应变,根据载荷和应变计算各截面的静态应变-弯矩比;
(3) 疲劳测试时,将各应变计获得的动态应变除以各截面静态应变-弯矩比即可获得各截面测试弯矩的试验数据[34]。
4 结论
疲劳测试作为衡量叶片疲劳寿命是否满足要求的试验,是叶片认证必不可少的一环。本研究对目前疲劳测试技术以及弯矩匹配方法进行总结,为大尺寸叶片疲劳测试技术的开展提供支持。
