基于功能损伤的装备有效毁伤幅员仿真方法研究

2020-02-18陈材石全尤志锋王亚东戈洪宇张芳

兵工学报 2020年1期

陈材，石全，尤志锋，王亚东，戈洪宇，张芳

(1.陆军工程大学石家庄校区，河北石家庄 050003；2.中国白城兵器试验中心，吉林白城 137001；3.32178部队，北京 100012)

0 引言

开展装备战斗损伤规律的研究，对于提升部队实战化水平、打赢高新技术背景下的现代战争具有十分重要的意义。充足的装备战斗损伤数据是进行战斗损伤规律研究的基础，虽然很多学者采用数值仿真的方式对战斗损伤规律相关问题进行了研究，但若缺少实际数据进行验证，其模型可信度则仍待考证。

目前，通过在靶场进行实装实弹试验，是获取损伤数据最有效的途径，在这方面国外起步较早[1]，国内近年来也多次开展此类型试验。鉴于高昂的试验成本，在试验过程中必须保证每次试验均能够收集到损伤数据，同时也能够根据试验需求达到最佳的试验效果，收集到最为有效的数据。其中需要解决的关键问题就是科学地布置弹药同受试装备(即弹药- 目标)之间的相对位置。为解决这一问题，主要从两个角度来进行考虑：一是从弹药毁伤幅员角度，即保证装备位于试验弹药的毁伤幅员内。孙业斌[2]给出了弹药爆炸后破片和冲击波有效杀伤范围的理论推导和经验公式；高鹏等[3]、刘建斌等[4]研究了不同条件下火箭杀伤爆破弹毁伤幅员的分布形态以及影响规律，通过对弹药发射和终端作用过程进行数学建模，建立了可视化仿真平台，实现了实时输出杀伤爆破弹毁伤幅员；王树山等[5]建立了针对不同打击对象的杀伤爆破弹综合威力评估模型。二是从目标毁伤幅员角度，即保证弹药位于受试装备的毁伤幅员内。刘怡昕[6]给出了部分老装备的毁伤幅员；王广彦等[7]以装备损伤概率为判断指标，建立了坦克中弹概率分布图；张庆捷等[8]根据炮兵作战行动的特点，分析了火炮毁伤幅员的计算方法。事实上，装备的损伤过程是一个弹药- 目标综合作用的过程，虽然有学者提出可根据所研究的具体问题灵活选择毁伤幅员[9]，但在实际试验时，仅从弹药或装备单方面的毁伤幅员进行弹药- 目标相对位置设计是不完善的。目前试验方案的设计多是依据其中某一种毁伤幅员，同时结合专家经验进行设计，虽能实现损伤数据的采集，但采集费效比过高，难以满足对损伤数据的现实需求。

本文针对战斗损伤试验中数据收集盲目性大且可用数据量少的问题，提出利用装备有效毁伤幅员进行弹药- 目标设置的方法。以破片打击为主要毁伤元，建立了装备有效毁伤幅员求解模型，提出了广义毁伤幅员和基于任务的装备功能损伤概率概念，分析了装备物理损伤仿真模型和装备功能损伤仿真模型的建立方法及步骤。为实现物理损伤仿真模型向功能损伤仿真模型的转化，提出了损伤注入的概念，并分析了其实施原理及方法。

1 装备有效毁伤幅员分析

假设试验场地面积为2Lf×2Ld，如图1所示，根据试验精度要求，用平行于两坐标轴且间距分别为Δx和Δy的两组平形线，将场地划分为网格状样式。

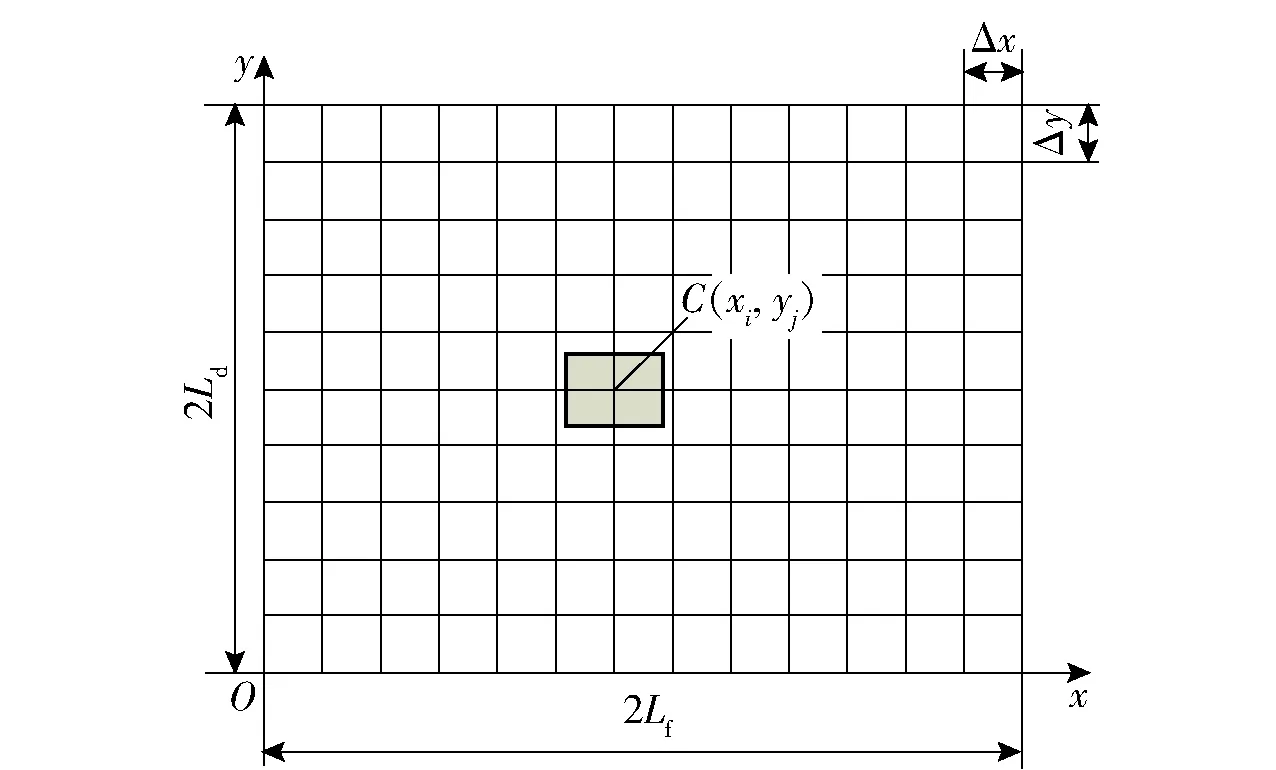
图1 试验场地划分示意图

以第j行第i列网格顶点C(xi，yi)作为单个装备的几何外形中心，设装备有效毁伤幅员面积为Se，其定义为

(1)

式中：Ph(x,y)为当试验弹药布置于试验场地中任意点(xi,yj)时，其爆炸后产生的破片对装备功能造成损伤的条件概率。显然，Ph(x,y)的值与毁伤因素的烈度和目标装备的结构、强度都有关系，前者取决于破片毁伤效能，后者取决于装备本身结构及性能特点。而破片毁伤效能的最直观体现是其对装备外形结构造成的物理损伤，如穿孔、变形等，在物理损伤的基础上，结合不同类型装备的结构和性能特点，可分析出由此造成的功能损伤。为此，将概率Ph(x,y)分解，可得

Ph(x,y)=P(KΔxΔy|H)·P(K|KΔxΔy)，

(2)

式中：H表示弹药在区域ΔxΔy中发生爆炸的事件；KΔxΔy表示装备发生物理损伤的事件；K表示装备发生功能损伤的事件；P(KΔxΔy|H)为弹药在区域ΔxΔy中爆炸后能够对装备造成物理损伤的条件概率，表示破片毁伤效能的强弱；P(K|KΔxΔy)为当装备发生物理损伤后，能够转化为装备功能损伤的条件概率，反映了装备结构和性能等本质属性的特点。则(1)式可转化为

(3)

这里引入广义毁伤幅员SΔ的概念，与有效毁伤幅员Se不同的是，广义毁伤幅员的范围更广，弹药在任意点(xi,yj)爆炸后，只要能够对装备造成物理损伤，则点(xi,yj)附近区域ΔxΔy就包含于广义毁伤幅员SΔ之内，而无需考虑此物理损伤是否对装备造成功能损伤。装备部件发生物理损伤，并不一定会引起装备的功能损伤，因此有效毁伤幅员Se隶属于广义毁伤幅员SΔ，二者相对关系如图2所示。

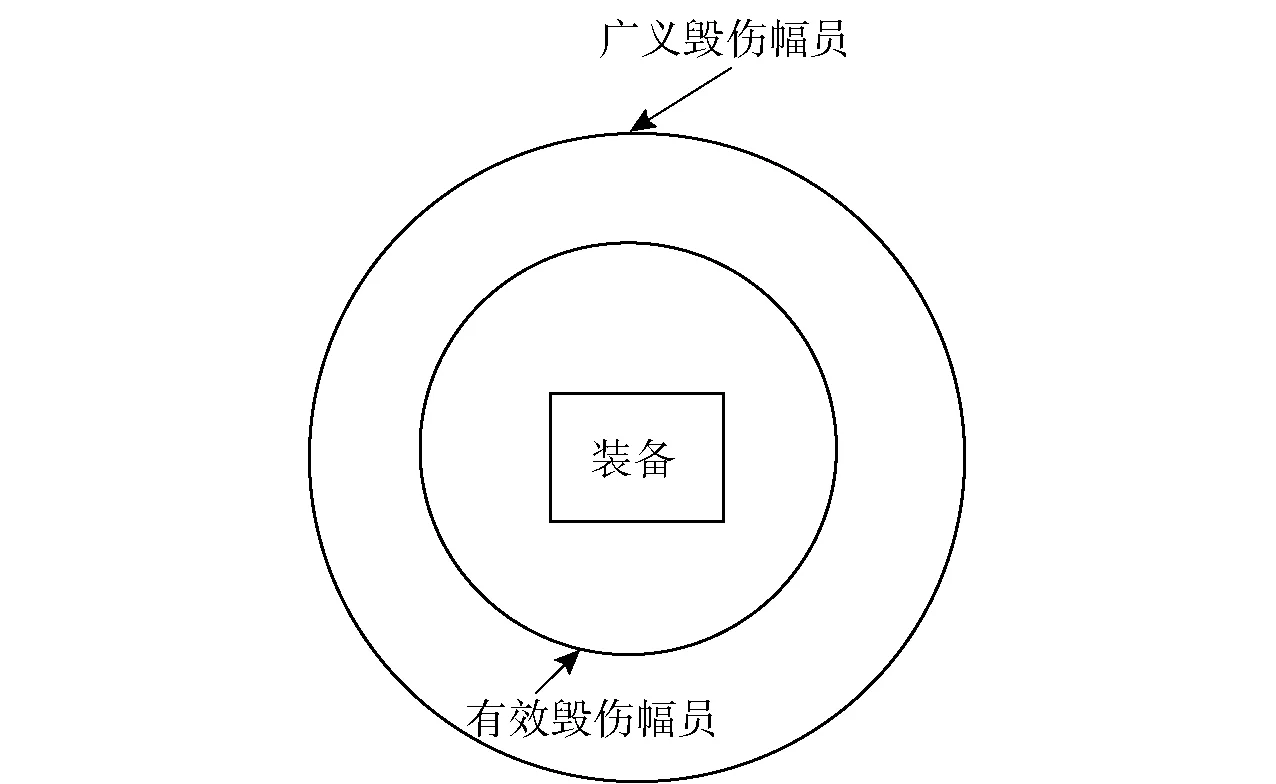
图2 两类毁伤幅员相对关系

于是，(3)式可转化为

Se=SΔ·P(K|KΔxΔy)，

(4)

(5)

由(4)式可知，若已知广义毁伤幅员SΔ，只要能够得到装备功能损伤概率，就可求得装备有效毁伤幅员，便可指导试验方案中弹药- 目标摆放相对位置的设计，实现战斗损伤数据的有效采集。因此，确定弹药广义毁伤幅员以及实现装备功能损伤概率的定量分析，是求取有效毁伤幅员的关键所在。

2 广义毁伤幅员分析

由广义毁伤幅员定义及(5)式可知，判断炸点附近区域ΔxΔy是否属于广义毁伤幅员的依据是装备是否发生物理损伤，而装备是否发生物理损伤既与弹药的爆炸强度有关，也与破片对装备的损伤机理有关。其中弹药爆炸强度决定了破片与装备作用的初始条件，损伤机理则影响着装备部件是否产生物理形态变化以及物理形态变化的程度及模式。

在确定广义毁伤幅员的过程中，建立装备物理损伤仿真模型是关键。

图3 装备物理损伤仿真原理

装备物理损伤仿真模型包括破片毁伤效能模型、面向破片损伤仿真的装备描述模型、装备破片损伤响应模型和装备损伤仿真过程模型。图3为装备物理损伤仿真原理和各类模型之间的关系，首先建立破片毁伤效能模型和装备描述模型，然后确定弹药和装备型号，以及弹药同装备之间的位置、角度等参数，利用装备损伤仿真过程模型进行驱动，获得破片与装备作用初始时刻的相关参数，再通过装备损伤响应模型确定装备部件的物理损伤模式及损伤程度。利用仿真获取的物理损伤数据，使用数理统计分析方法，即可确定弹药的广义毁伤幅员。

2.1 破片毁伤效能模型

破片从形成到飞散受到诸多因素影响，包括装药类别、装药质量、弹药长径比以及破片形状、质量等。这些因素共同决定破片打击装备的毁伤效能大小，为了迅速直观地获知破片的毁伤威力，通常以破片飞散角和破片初始速度作为判断标准[10]。随着计算机仿真技术的迅速发展，加之数值模拟具有成本低、可重复性好、数据量丰富的特点，辅以少量实弹试验数据进行仿真参数修正，就可在允许误差范围内真实还原实弹爆炸情景，因此成为获取破片毁伤效能数据最经济和最可信的方法。破片毁伤效能模型的建立原理如图4所示。首先分析弹药特点，明确弹药几何尺寸、材料特性、装药质量和破片制造工艺等关键参数，利用这些参数在仿真软件中建立弹药模型；随后通过数值仿真的方式模拟弹药爆炸的全过程，获得破片飞散角和速度参数，在此基础上，利用实弹试验数据对仿真数据进行修正，直到二者误差值在允许范围内为止；最后，利用仿真获取的丰富数据，即可建立完善的破片毁伤效能模型。

图4 破片毁伤效能模型原理图

2.2 面向破片损伤仿真的装备描述模型

破片损伤是各种常规弹药以及导弹对装备损伤的最常见形式[1]。通过建立装备描述模型，能够真实描述装备零部件材料的物理、化学特性，以及零部件的几何特性和空间位置信息。其基本原理如图5所示，将装备描述模型划分为4个层次，即装备—基本项目—基本元素—基本几何元素。图5中p、q、w分别为相应的基本项目、基本元素和基本几何元素的数量。

首先，将装备描述为若干基本项目，基本项目包括基本功能项目和基本结构项目，前者是指那些受到损伤后将对作战任务产生致命性影响的项目，后者是指可能对基本功能造成遮挡关系的项目，将装备描述成由基本项目构成，可大大简化装备结构。其次，将每个基本项目分解为若干具有一定形状、机械、物理和化学特性的基本元素。再将各基本元素分解为若干具体几何形状的基本几何元素，最终建立起装备结构简化模型。

2.3 装备破片损伤响应模型

当破片以不同的形状、速度、入射角度等特征参数作用于装备不同零部件时，需要迅速准确地知道零部件发生了何种类型的损伤模式，这是建立装备物理损伤仿真模型的关键。本文通过损伤相图的方式，确定装备部件的损伤模式及损伤阈值。装备部件的损伤模式通常表现为几种离散化的具体形式，如跳飞、嵌入、穿孔等，而装备部件的结构响应特性则表现为连续性的变量，如靶板的侵彻深度，这就需要将连续的结构响应特性离散化为具体的战斗损伤模式，是损伤相图的构建搭建基础。结构响应特性与战斗损伤模式二者间映射关系如图6所示。

图5 装备描述模型分层结构示例

图6 结构响应特性与典型损伤模式之间的映射关系

以破片侵彻靶板为例说明建立映射关系的方法和过程。影响破片侵彻靶板响应特性的输入参数主要有破片入射速度v、入射角度α和破片质量mf.若考虑破片侵彻靶板的深度h这一结构响应特性，则有h=g(v,α,mf)，其中函数g(·)是数值模拟软件所能够反映出的映射关系。由于数值模拟软件只能够分析出破片侵彻靶板时的侵彻深度h，无法辨识靶板的损伤模式，因此需要结合软件的可视化功能和已有经验公式，判断分析在不同的侵彻深度下能够产生的损伤模式，从而建立起装备物理损伤模式同破片侵彻深度之间的映射关系。如(6)式所示，h与损伤模式Mk之间的映射关系为

(6)

式中：Mk为装备部件的第k种损伤模式；[hk-1,hk]表示破片侵彻靶板发生损伤模式Mk时所对应的侵彻深度。

由以上分析可知，复合函数f(g(v,α,mf))反映出了输入参数v、α、mf同损伤模式Mk之间的映射关系，而装备部件损伤相图反映的也正是这个映射关系。在实际运用中，为降低损伤相图的构建难度，同时加快损伤模式判别速度，故只采用二维形式的损伤相图，每张图中反映两个参数对装备部件损伤模式的影响规律，其查询示意图如图7所示。

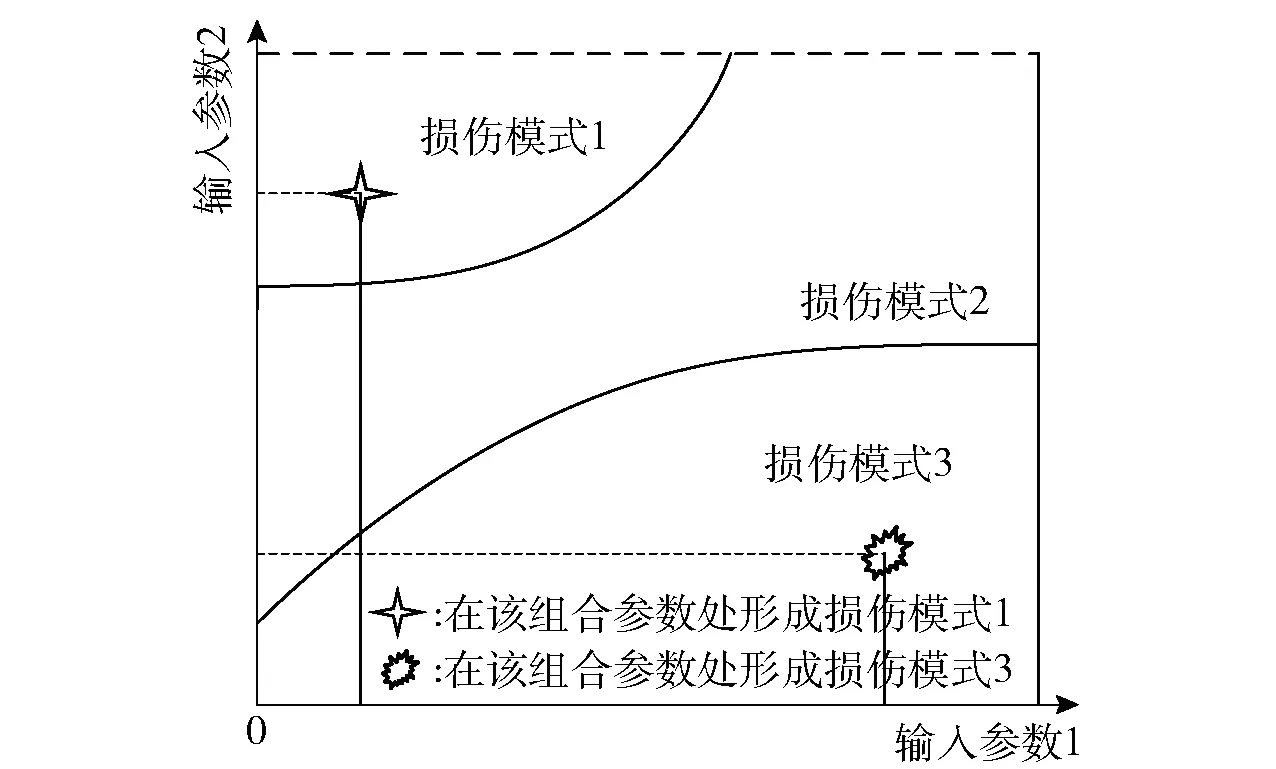
图7 损伤相图查询方法示意图

在此基础上，建立损伤相图数据库，实现不同输入参数同损伤相图的相互关联，从而在一次仿真中，能够根据输入参数查找到对应的损伤相图，并确定装备部件的损伤模式。

2.4 装备损伤仿真过程模型

图8 装备破片损伤仿真过程模型

装备损伤仿真过程模型是装备物理损伤仿真的驱动器，通过建立损伤仿真过程模型，能够保证装备物理损伤仿真模型的正确平稳运行。单个装备在多枚弹药作用下的破片损伤仿真流程如图8所示。首先确定装备部件和弹药数量，运用Monte Carlo法生成弹着点散布坐标[11]，再根据弹药参数，模拟得到单枚弹药爆炸后形成的破片场数据，分析破片在空中的飞行规律，确定破片到达装备不同部件时的初始毁伤参数，最后调用破片损伤响应模型，确定装备部件最终的损伤模式。

3 装备功能损伤仿真模型的建立

装备功能损伤仿真模型是在装备物理损伤仿真模型上衍生出的更高层次损伤模型，王广彦等[12]从定性分析角度对二者之间的联系和转换方法进行了初步分析，而要实现装备有效毁伤幅员的划分，则需要建立定量化的分析模型，这是装备功能损伤仿真模型的核心内容。在建立装备物理损伤仿真模型的基础上，本文提出采用损伤注入的方法，实现装备功能损伤仿真模型的建立。

3.1 装备物理损伤仿真模型与装备功能损伤仿真模型的映射关系

装备物理损伤仿真模型中，装备零部件的损伤模式具有多态性的特点，导致装备功能损伤也呈现出多态性的特点。设装备某子系统功能为F，组成此子系统的零部件形态分别为C1,C2,…,Ca，则有

F=fd(C1,C2,…,Ca)，

(7)

式中：函数fd(·)为装备物理损伤仿真模型同装备功能损伤仿真模型间的映射关系；a为组成此子系统的零部件形态总数量。当零部件形态C1,C2,…,Ca处于完好状态时，子系统能够正常运行，当装备发生物理损伤后，子系统相应零部件则发生ΔC1,ΔC2,ΔC3,…,ΔCa的形态变化，这种变化可能对子系统性能带来影响，并向上影响到装备功能。使用自然语言的方式描述这种关系为

IFC1=C1+ΔC1,C2=C2+ΔC2,…,Ca=Ca+ΔCa，THENF+ΔF=f(C1+ΔC1,C2+ΔC2,…,Ca+ΔCa)，

(8)

式中：ΔF为子系统功能的变化。由于零部件几何外形各异，其在装备各子系统中的运行机制也各有特点，单纯的物理损伤有时并不会对装备功能造成影响，或者在类似的物理损伤模式下，不同的零部件对装备功能的影响程度不同。因此若要得到定量且精确的功能损伤结果，还需结合装备运行机制进行分析。

3.2 装备损伤注入概念及实施步骤

装备损伤注入可类比装备故障注入，后者是针对装备在非战斗情况下的故障模式进行研究，前者是针对装备在战斗情况下的损伤模式进行研究。

3.2.1 损伤零部件种类和损伤模式类型的确定

按照已有的分类规则对受损零部件种类进行划分，同时通过零部件的损伤特征对其损伤模式进行判断和划分。

1)损伤零部件分类分析。装备机械零部件种类繁多，不同结构特征的零部件在遭到破片攻击后的损伤模式多种多样，而对于同一个损伤模式，当其分别发生在结构特征不同的零部件时，对装备性能带来的影响也将不同。可从两个角度对受损零部件进行分类：1)按照零部件结构特征进行分类，参照机械零件分类编码系统[13]，将装备机械零部件分为回转体和非回转体两类，每类又可继续细化，如表1所示；2)按照机械零部件运动特性分类，以机械零部件在装备系统中是否参与机械运动作为判断标准，将其分为静止类零部件和运动类零部件。

表1 机械装备零部件分类

2)零部件常见损伤模式分类分析。按照物理损伤是否立即造成装备功能损伤，将装备物理损伤类型分为隐性损伤和显性损伤。隐性损伤指当装备发生物理损伤后，虽然零部件的形态发生了一定的变化，但在短期内仍能维持正常的运行状态，只有当某些参数值超过最大阈值时，系统才会出现功能损伤的损伤类型。而若装备零部件发生物理损伤后，装备功能立即受到影响，这样的损伤则称为显性损伤。根据破片打击装备的损伤机理以及装备机械部件的结构特点，可得到以下5类常见损伤模式：①磨损损伤；②断裂损伤；③变形损伤；④运动副损伤；⑤运动特性改变损伤。

3.2.2 装备损伤描述模型的建立

装备损伤描述模型是对装备物理损伤的抽象化描述，同时也是对物理损伤公共属性的表征，不同的损伤描述模型具有不同的损伤注入方法。对于某一类确定的机械零部件，由于不同损伤模式的损伤机理不同，使得零部件表现出的功能损伤特点也各不相同；而对于某一类确定的损伤模式，由于不同类型零部件的结构特征和运动特性不同，也就造成最终的功能损伤特点不同。对于这种复杂的对应关系，需要找到它们对装备功能产生影响的共性，即装备零部件在发生物理损伤后其本质属性的变化。设发生变化的本质属性为E，损伤模式为α，零部件类型为β，它们之间的关系为

E=fb(αr,βs)，

(9)

式中：fb表示损伤模式同零部件类型之间的作用关系；r=1,2,…,mt，s=1,2,…，nt，mt和nt分别为损伤模式和零部件类型的数量。不管零部件类型和损伤模式如何组合，其最终结果都是对装备某一本质属性产生影响，这些本质属性不仅反映了装备结构损伤及运动特性的变化特点，更为损伤注入方法的确定奠定了基础。损伤描述模型建立过程如图9所示。

图9 装备描述模型建立过程

由图9可知，不同损伤模式的主要损伤特点比较明显，但是它们的损伤机理、损伤形式等基本属性也存在着交集。因此，当某一零部件同时发生几类损伤模式后，需要对这些损伤模式的本质特征进行分析，找出它们对装备性能的共同影响，即找出不同损伤模式所能影响到的同一个装备基本属性，从而建立装备损伤描述模型。对于装备机械零部件，可建立3类损伤描述模型：1)装备部件几何属性变化模型；2)装备运行工况变化模型；3)装备特征参数变化模型。

3.2.3 损伤注入的实施

通过建立装备损伤描述模型，能够对不同损伤模式界定划分明确的界线，而不同的损伤描述模型又对应不同的损伤注入方式，根据3.2.2节中建立的装备损伤描述模型，建立以下3种类型的损伤注入方式：

1)改变装备几何物理属性。利用仿真平台中的布尔运算命令，直接在虚拟样机模型上通过改变装备几何外形结构来实现损伤注入，对于损伤形式比较复杂的情形，则需要借助第三方建模软件(如三维计算机辅助设计软件Pro/E、Solidworks等)构造出发生物理损伤后的装备模型，再通过专业接口将模型导入仿真平台中进行运算。

2)改变装备工况设置。工况是装备运行时所处外部环境的总称，其对机械装备最直接的影响就是对某些零部件的应力水平产生影响，从而成为诱发装备功能损伤的重要因素之一。在仿真平台中，有专门的模块对零部件的应力、负载和转速等工况进行设置，能够迅速方便地进行损伤注入。

3)改变装备部件特征参数。对某些损伤模式，可以抽象为装备部件的某些特征参数发生了改变。如弹簧由于破片侵彻发生刚度下降，可等效为其刚度系数k的减小。此外，还可以根据功能损伤仿真模型的需求对材料的强度、摩擦系数等特征参数进行调整。

实施损伤注入，需要首先建立能够反映实际装备在未受损情况下正常运行状况的虚拟样机模型，其建立方法已有相关文献进行分析[14-16]，本文不再赘述。通过在虚拟样机模型中实施损伤注入，即可通过仿真得到受损后的装备功能损伤规律。

4 装备功能损伤概率定量分析

与装备物理损伤仿真不同的是，装备功能损伤概率分析，只需关注到基本项目层即可。此外，在实际作战中，由于装备所承担的作战任务不同，对其发生功能损伤的判断标准也就不同，如雷达在一次作战任务中轮胎被击中报废，虽然其运动功能遭到了破坏，但在天线完好的情况下，依然能够执行搜索、定位的功能。在靶场试验中，有时会将装备的某一项或某几项功能作为特定的任务对象，而其他功能在本次试验中则较为次要或忽略不计，故本文提出基于任务的装备功能损伤概率，从装备完成具体任务角度出发对其功能损伤概率进行计算。

设基于任务的装备功能损伤概率为Pt，其定义为

(10)

式中：nb为装备基本项目数量；Au为针对装备具体任务所确定的基本项目赋值系数，若基本项目u对装备此次任务有影响，则赋值Au=1，若无影响，则赋值Au=0；Pu为基本项目u所对应的功能损伤概率，设仿真运行N次，有

(11)

PuI为基本项目u在第I次仿真中的功能损伤概率，其确定需结合不同基本项目的结构特点及运行机理。通过构造仿真模型，对遭受物理损伤的基本项目进行分析，利用仿真结果和损伤判据来判断基本项目是否发生功能损伤，从而在此基础上求取功能损伤概率。

5 实例分析

本文在装备物理损伤仿真建模的基础上，开发了装备战斗损伤仿真平台，以某型预制破片弹药为威胁源，某型自行火炮为受试装备，对装备的有效毁伤幅员进行了分析。

5.1 破片毁伤效能模型的建立

如图10所示，通过建立弹药数值仿真模型，利用实弹试验数据对仿真数据进行修正，即可得到弹药破片的速度及飞散角分布规律。

图10 破片毁伤效能参数获取原理图

5.2 装备描述模型的建立

对某型自行火炮，按照装备—基本项目—基本元素—基本几何元素 4个层次绘制其基本项目结构树，如图11所示。在此基础上，根据基本几何元素层几何元素的参数信息，建立该型装备的结构简化模型，如图12所示，图中X轴、Y轴、Z轴为装备战斗损伤仿真平台中建模型块坐标轴。

图11 某型自行火炮基本项目结构树

5.3 装备损伤响应模型的建立

运用AUTODYN有限元仿真平台建立破片及装备部件的实体模型，设置部件材料参数以及破片毁伤效能参数，通过一次仿真得到一组实验结果；改变破片毁伤效能参数进行多次仿真，将不同破片毁伤效能参数下的实验结果在坐标系中进行标记，利用回归分析的方法画出对应曲线，得到装备部件在此坐标系下的损伤相图，其过程如图13所示。改变破片毁伤效能参数类别，即可得到破片打击装备的损伤相图库。

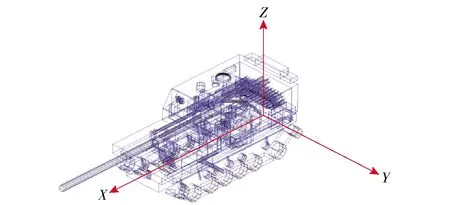
图12 某型自行火炮实体结构简化模型

5.4 装备物理损伤仿真的实施

利用装备损伤仿真过程模型进行驱动，即可在装备战斗损伤仿真平台中对该火炮的物理损伤情况进行分析。仿真过程如图14所示，平台以三维可视化的方法再现了弹药模型、装备模型和二者间的相互作用，可得到装备零部件的损伤情况、损伤模式以及损伤程度。

5.5 广义毁伤幅员的确定

为了判定炸点(xi,yj)附近区域ΔxΔy是否在弹药广义毁伤幅员之内，需按照图1中划分网格的方式，在火炮周围设置若干炸点，得到弹药在不同炸点爆炸后装备各部件的命中弹片数，以弹片总数为试验指标，利用假设检验的方法即可求得广义毁伤幅员，具体计算方法见文献[17]。最终可得火炮广义毁伤幅员如图15所示，其中炸点间距Δx、Δy均为1 m，总面积达388 m2.

5.6 装备有效毁伤幅员的确定

假设某次试验任务主要是采集火炮传动系统的损伤数据，由(10)式可知，只需要对火炮传动系统进行功能损伤建模。以传动系统中变速箱为例，结合5.4节物理损伤仿真结果，可知变速箱损伤模式主要为齿轮齿面的切削。根据3.2.2节中装备损伤描述模型的分析，确定变速箱损伤注入方式为改变几何物理属性，即根据物理损伤程度对轮齿进行齿面的切削，由此可建立变速箱功能损伤仿真模型，如图16所示。

齿面的切削会对轮齿危险截面处的应力产生影响，当切削量达到一定程度时，会使危险截面处的应力值大于轮齿许用弯曲应力。一般情况下，轮齿许用弯曲应力可通过试验的方法获取，其经验表达式为

(12)

式中：σFlim为齿轮的齿根弯曲疲劳极限；SFmin为弯曲疲劳强度的最小安全系数；YN为弯曲疲劳强度计算的寿命系数；YX为尺寸系数。通过查表[18]，可得4个参数的具体数值，如表2所示。将表2中数值代入(12)式中，可得轮齿许用弯曲应力σF为278 MPa.

图13 装备损伤相图绘制过程(右为生成相图)

图14 物理损伤仿真过程可视化场景

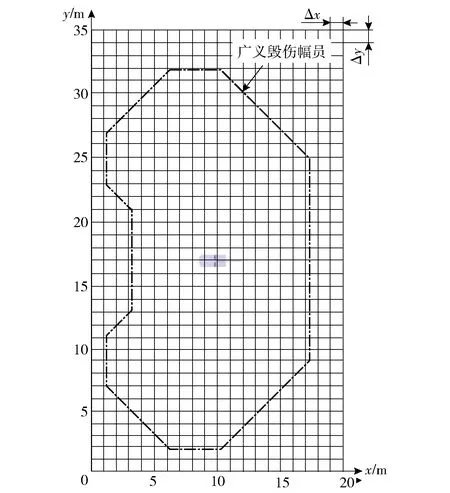
图15 广义毁伤幅员示意图

图16 齿轮传动系统功能损伤模型

在ADAMS仿真平台中对变速箱的运行进行仿真，可得不同切削程度下齿根处的最大应力值σmax.当损伤轮齿根部应力σmax超过σF时，轮齿就会断裂，从而使变速箱发生功能损伤，以此为判断标准，可得轮齿功能损伤图，如图17所示。

表2 许用弯曲应力相关参数

图17 齿轮轮齿功能损伤图

将上述仿真过程重复20次，由(11)式可得变速箱功能损伤概率为0.60.同理，可得传动系统其余部件功能损伤概率，由(10)式可求得在此任务下火炮的功能损伤概率为0.71.因此由(4)式可知，某型火炮有效毁伤幅员为275.48 m2，其示意图如图18所示。将弹药布置在有效毁伤幅员范围内，即可保证收集到有效的满足此次试验任务的火炮战斗损伤数据。