轻骨料混凝土桥梁地震易损性分析

台玉吉，惠迎新，师新虎，金宝宏，徐赞

轻骨料混凝土桥梁地震易损性分析

台玉吉1，惠迎新1，师新虎2，金宝宏1，徐赞1

(1. 宁夏大学 土木与水利工程学院，宁夏 银川 750021；2. 西南交通大学 土木工程学院，四川 成都 610031)

为提高强震区桥梁的抗震性能，采用轻骨料混凝土替代普通混凝土以降低结构自重、提高墩柱变形能力，从而降低地震响应。以一座强震区典型中小跨径连续梁桥为研究对象，基于OpenSees建立轻骨料混凝土桥梁有限元分析模型，进行非线性时程分析，生成地震易损性曲线来评估桥梁的抗震性能。研究结果表明：与普通混凝土桥梁相比，仅上部结构或下部结构采用轻骨料混凝土对降低桥梁整体的损伤概率并不明显，而全桥均采用轻骨料混凝土的桥梁能够显著降低桥墩、桩基和支座的损伤概率以及桥梁整体的损伤概率。建议在强震区进行桥梁建设时，全桥均采用轻骨料混凝土来替代普通混凝土以提高桥梁抗震性能。

桥梁工程；轻骨料混凝土；地震易损性；概率性地震需求模型；一阶界限法

桥梁在以往地震中的震害形式大致可分为主梁破坏、支座破坏、墩台破坏、桩基破坏及其他构件破坏。其中桥墩、桩基和支座在地震力作用下发生损伤的概率最高，如汶川地震中的百花大桥(桥墩弯曲破坏)、美国洛马普列塔地震中Struve Slough 桥(桩基侧向弯曲变形)、加拿大Saguenay地震中的Shipshaw独塔斜拉桥(支座的抗拉力锚杆断裂)。桥墩、桩基和支座作为桥梁的重要组成部分，其抗震性能直接影响桥梁整体的失效概率，因此有必要降低关键部位的地震失效概率，从而提高桥梁整体的抗震性能。降低桥梁失效概率可通过提高结构的抗震能力或降低地震需求，提高墩柱的抗震能力可通过增加箍筋数量或提高混凝土强度，但地震需求、结构造价以及施工难度也随之增加。降低地震需求可选用质量轻、变形能力好的结构材料，轻骨料混凝土因具有轻质、高强和变形能力好的特点，将其应用于桥梁结构是降低桥梁损伤概率的有效途径。而文献中关于轻骨料混凝土的研究主要集中在材料性能[1-2]、结构构件[3]和房屋建筑[4]抗震效果，在桥梁方面研究较少，沈永林等[5-6]对轻骨料混凝土桥梁进行了地震响应研究，均指出轻骨料混凝土能够降低墩底响应，但同时增加了墩顶位移。降低地震需求的同时也可能降低结构的抗震能力，而且桥梁作为一个整体，各构件之间相互作用，仅通过单一构件并不能说明轻骨料混凝土在桥梁结构中的整体抗震效果，而易损性分析能够很好地表达结构在地震作用下的抗震效果和损伤概率，但关于轻骨料混凝土桥梁地震易损性方面，目前鲜有研究。因此，本文以一座强震区常规中小跨连续梁桥为例，分别建立普通混凝土和轻骨料混凝土桥梁的有限元模型，选取100条实测地震波进行非线性时程分析，生成地震易损性曲线，以概率方法对轻骨料混凝土桥梁的抗震性能进行分析。

1 轻骨料混凝土模拟

本构关系反映物质宏观性质的数学模型，准确模拟混凝土的本构关系是确保结构地震易损性分析正确的关键所在。在本文中，轻骨料混凝土采用OpenSees有限元程序进行模拟。

1.1 轻骨料混凝土本构关系

在OpenSees中提供了常用的6种混凝土本构模型，其中Concrete02本构模型(如图1所示)考虑了混凝土的拉伸强化并将受拉软化段处理为线性变化[7]，能够很好地模拟纵向钢筋和箍筋对核心混凝土的约束效应[8]以及混凝土压弯构件在反复荷载作用下的滞回特性[9]，在相关文献[10]中应用较多，因此，本文对于普通混凝土模拟采用Concrete02本构模型。根据文献[11]可知，轻骨料混凝土与普通混凝土的本构关系相似，2种混凝土主要在混凝土密度c，弹性模量，混凝土达到轴心抗压强度设计值时的压应变0和极限压应变cu有所差别，因此对轻骨料混凝土可采用Concrete02本构模型。c和可根据《轻骨料混凝土结构技术规程》[12]进行选取，对于0和cu取值，王振宇等[13]在对结构轻骨料混凝土进行大量研究得出了LC10-LC55的0和cu的取值，陈桂斌等[14]通过数值模拟方法得出了轻骨料混凝土0和cu的结果并与王振宇试验所得结果进行了对比，两者结果基本一致。因此，在本文中0和cu的取值采用王振宇实验结果进行模拟，LC50，LC30以及相应的普通混凝土所对应的Concrete02模型的参数如表1所示。

图1 Concrete02本构模型

图2 理论与实验本构关系对比

以LC30为例，通过表1计算得出的数据，代入到Concrete02本构模型中，绘制出LC30的本构关系并与文献实验结果进行对比，由图2可知模拟方法正确。

1.2 钢筋本构模型

钢筋在单向受拉时会经历弹性阶段、屈服阶段、强化阶段和破坏阶段，在地震力较大时，钢筋同样会发生这个过程。本文采用streel01对普通钢筋进行模拟，该模型能较好地描述反复荷载作用下钢筋屈服和强化过程，因而应用广泛，其本构关系如图3所示。

图3 streel01本构模型

2 桥梁地震易损性分析

2.1 构件易损性

桥梁结构的地震易损性分析是建立桥梁结构损伤与地震动强度之间的联系过程，涉及到地震需求、抗震能力和地震动强度指标，由于结构自身的随机性远小于地震动的随机性，因此本文没有考虑模型的不确定性。易损性理论分析法主要有非线性动力分析、非线性静力分析和反应谱分析，其中非线性动力分析又分为基于概率地震需求分析的线性拟合法(PSDA)[15]、基于增量动力分析的超越极限状态的频数分析法(IDA)[16]和基于损伤指数的能力需求比模型的曲线拟合法[17]，相比之下PSDA不需要进行地震波缩放，计算量较少，因此本文采用PSDA进行计算地震易损性。

式中：和为统计回归系数。

式中：D为第条地震波作用下结构的地震需求峰值；为地震波的数量。

3) 通过上式计算，将其代入到基于概率性地震需求的地震易损性函数，该函数可表示为：

式中：S和β表示抗震能力的均值和对数标准差。

2.2 系统易损性曲线

桥梁是由不同结构部位组成的整体，不同构件的地震易损性曲线不同，不能够完全表明结构整体的损伤概率，仅通过构件的最大损伤概率来评估结构系统的易损性，往往会严重低估结构系统的抗震能力，因此需要采用系统易损性进行分析。目前常用的方法有一阶界限法(宽界限法)和二阶界限法(窄界限法)。一阶界限法计算量少，结果保守，因此本文采用一阶界限法进行计算。

一阶界限法假定不同构件的破坏概率之间是相互独立的，其相关性=0[19]：

式中：sys为全桥系统失效概率；P为第种构件发生破坏的概率。假设各构件串联，将构件破坏概率的最大值作为结构失效概率的下限值；假设各构件并联，全部构件失效的概率作为结构失效概率的上限值。

表1 Concrete02模型中各试件混凝土参数值

注：1)为箍筋的体积配箍率；yh为钢筋的屈服强度；本文中桥墩和桩基的体积配箍率分别为0.25%和0.24%，钢筋屈服强度为335 MPa。

2)fc为核心混凝土和保护层混凝土参数的比例系数。

3 工程算例

以一座强震区典型中小跨径连续梁为例，桥跨布置为4×30 m，桥宽12.5 m，桥墩采用柱式墩、桩基础，墩高均为20 m，桩基长度均为33 m；支座在过渡墩和连续墩处均采用普通板式橡胶支座。桥墩和桩基的纵向钢筋配筋率分别为1.3%和1.2%，桥址处地面峰值加速度为0.2。桥梁总体布置图如图4所示。

单位：cm

采用OpenSees有限元程序建立三维有限元模型，主梁、盖梁及系梁均采用线弹性梁柱单元模拟，桥墩和桩基础采用非线性梁柱单元模拟，利用零长度单元模拟桩土作用，弹簧刚度根据土层的m法值进行计算。普通板式橡胶支座采用零长度单元模拟，水平剪切刚度根据支座型号选取，通过软件OSLite可显示有限元模型如图5所示。

图5 有限元模型

3.1 方案设计

为研究上部结构、下部结构或全桥采用轻骨料混凝土对结构地震易损性的影响。设计以下4种不同方案分别建立有限元模型。

方案1：上部结构和下部结构分别采用普通混凝土C50和C30；

方案2：上部结构采用轻骨料混凝土LC50，下部结构采用普通混凝土C30；

方案3：上部结构和下部结构分别采用轻骨料混凝土LC50和LC30；

方案4：上部结构采用普通混凝土C50，下部结构采用轻骨料混凝土LC30。

3.2 地震波的选取

依托桥梁地处Ⅱ类场地，地面峰值加速度为0.2，场地特征周期为0.45 s。采用E2水平向设计反应谱在太平洋地震工程研究中心(PEER)中进行地震波的匹配，从东西和南北分量分别收集合成大的地震数据记录。选取符合场地类型为Ⅱ类场地的100条地震波，地震波的PGA分布如图6所示，由图6可知，所选地震波的PGA在0.1~0.3范围内较多，100条地震波的反应谱图如图7所示，其中粗线为100条地震波的平均值，在地震易损性分析时未调整其峰值加速度，按其实际记录情况输入。

图6 100条加速度时程地震波PGA分布图

图7 100条加速度时程地震波的反应谱图

seismic waves

3.3 损伤指标的确定

对桥梁进行地震易损性分析，要确定结构的损伤等级和损伤指标[20]。损伤等级可分为无损伤、轻微损伤、中度损伤、严重损伤和完全损伤5个等级，用来定义墩柱的损伤指标有曲率延性、位移延性、钢筋应变、混凝土应变、侧移角、残余位移、塑性转角、滞回耗能和Park-Ang 指标[21]，定义支座损伤指标有位移、位移比及剪切应变等。

3.3.1 桥墩和桩基

通常定义桥墩的损伤指标采用曲率延性和位移延性。但关于定义桩基损伤指标的研究相对较少，未有明确界定损伤状态的方法。因此本文对桥墩和桩基均采用曲率延性比作为损伤指标。采用Xtract对墩底和桩顶截面进行弯矩曲率分析，分别以纵筋的首次屈服曲率、等效屈服曲率和混凝土应变达到0.004时的曲率和极限曲率来定义轻微损伤、中等损伤、严重损伤和完全损伤[22]，损伤指标计算如式(6)所示，其中桥墩和桩基的纵筋首次屈服曲率如表2所示。

3.3.2 支座

普通板式橡胶在地震作用下具有良好的柔性，能够产生一定的剪切变形。从安全的角度考虑，支座的容许剪切应变γ需计入安全系数，按下式计算[23]：

式中：max为地震作用下容许的最大支座相对位移；a为容许剪切应变。

规范规定固定型支座设计剪应变为1.0，容许剪应变为1.5，极限剪应变为2.5，本文支座选择的剪切应变为1.0，1.5，2.0和2.5。

表2 4种方案桥墩和桩基纵筋首次屈服曲率

4 分析与讨论

4.1 概率需求模型

对4种方案模型进行纵向激励，记录构件的最大动力响应和对应的地面加速度峰值，将其在对数坐标中绘制并进行直线拟合，得到如图8所示的概率性地震需求模型。从图8可以看出，方案3和方案4的桥墩和桩基的地震需求明显小于方案1和方案2的，方案2和方案3的支座地震需求明显小于方案1和方案4的，综合来看，方案3能够同时降低桥墩、桩基及支座的地震需求，具有明显降低地震响应的效果。

(a) 桥墩；(b) 桩基；(c) 支座

4.2 构件易损性曲线

结构的地震易损性还与结构的抗震能力有关，因此通过2.1所述方法绘制出地震易损性曲线，图9为地震力作用下桥墩、桩基和支座的地震易损性曲线，对桥墩截面进行分析绘制P-M曲线如图10所示。就桥墩的损伤概率来看，全桥采用轻骨料混凝土的损伤概率相比普通混凝土降低最为明显，由表2可知，虽然抗弯能力有所降低，但地震响应降低更为显著，因此使得损伤概率降低，其次是下部结构采用轻骨料混凝土的桥梁，也能够明显降低桥墩和桩基的损伤概率。上部结构采用轻骨料混凝土的桥梁反而较普通混凝土桥梁的桥墩更易受损，由图10可知，当墩底轴力在段时，随着轴力的增大其抗弯能力也随之提高，经计算4种方案的墩底轴力均在段，由此可知方案2虽然上部结构采用轻骨料混凝土后能够明显降低结构自重，从而降低墩底响应，但是由于自重减轻导致墩底轴力降低，其墩底抗弯能力也随之降低，桥墩的抗弯能力相比方案1明显减小，因此导致墩底更易受损。对于上述桥墩易损性的结论同样适用于桩基，可见下部结构采用轻骨料混凝土能够明显降低桥墩和桩基的损伤概率。

图10 普通混凝土和轻骨料混凝土桥墩P-M曲线

支座损伤概率最低的是上部结构采用轻骨料混凝土和全桥采用轻骨料混凝土的桥梁，显然降低上部结构自重能够明显降低支座位移，从而降低支座损伤概率，而仅下部结构采用轻骨料混凝土的桥梁与普通混凝土桥梁的支座损伤概率基本一致，可见上部结构采用轻骨料混凝土能够明显降低支座损伤概率。

4.3 系统易损性曲线

采用一阶界限法计算形成系统易损性曲线如图11所示，从图11可以看出，全桥采用轻骨料混凝土桥梁的损伤概率明显小于其他3种方案，可见全桥采用轻骨料混凝土能够明显降低强震区桥梁的损伤概率。因此，在强震区进行桥梁建设时，建议采用全桥轻骨料混凝土桥梁，能够明显降低不同结构构件和结构整体的损伤概率。

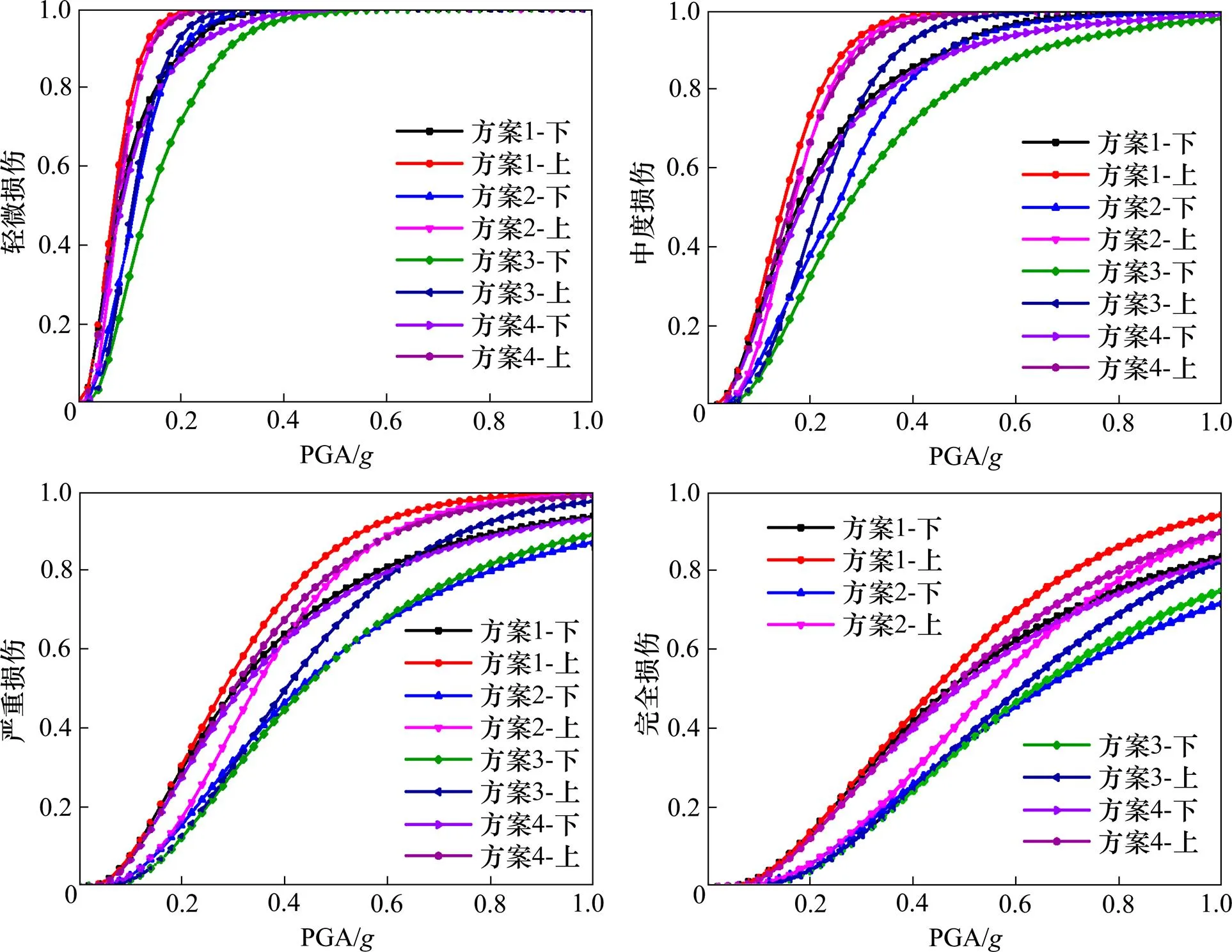
图11 系统易损性曲线

5 结论

1) 与普通混凝土桥梁相比，仅下部结构采用轻骨料混凝土的桥梁能够明显降低墩底和桩顶的地震需求；仅上部结构采用轻骨料混凝土的桥梁能够明显降低支座的地震需求；全桥采用轻骨料混凝土的桥梁能够同时降低桥墩、桩基和支座的地震需求。

2) 仅上部结构采用轻骨料混凝土的桥梁与普通混凝土桥梁相比能够明显降低支座损伤概率，但桥墩和桩基的损伤概率反而有所提高；仅下部结构采用轻骨料混凝土的桥梁能够明显降低桥墩和桩基的损伤概率，但不能降低支座的损伤概率；全桥采用轻骨料混凝土的桥梁能够明显降低桥墩、桩基和支座的损伤概率。

3) 从桥梁整体抗震性能来看，全桥采用轻骨料混凝土的桥梁具有明显降低结构整体损伤概率的优势，因此在强震区进行桥梁建设时建议采用全桥轻骨料混凝土桥梁。

[1] Rossignolo J A, Agnesini M V C. Durability of polymer-modified lightweight aggregate concrete[J]. Cement and Concrete Composites, 2004, 26(4): 375-380.

[2] Kayali O. Fly ash lightweight aggregates in high performance concrete[J]. Construction and Building Materials, 2008, 22(12): 2393-2399.

[3] 潘亮, 魏慧, 刘喜, 等. 高强轻骨料混凝土柱抗震性能研究进展[J]. 世界地震工程, 2016, 32(4): 259-265. PAN Liang, WEI Hui, LIU Xi, et al. Progress of study on seismic behavior of high-strength lightweight aggregate concrete columns[J]. World Earthquake Engineering, 2016, 32(4): 259-265.

[4] 刘哲锋, 苏志力, 杨伟军. 轻骨料混凝土与普通混凝土框架结构的抗震性能分析[J]. 建筑结构, 2010, 40(2): 22-24, 32. LIU Zhefeng, SU Zhili, YANG Weijun. Seismic performance analysis of lightweight aggregate and ordinary concrete frame structures[J]. Building Structure, 2010, 40(2): 22-24, 32.

[5] 沈永林, 马芸仙. 普通混凝土和轻质混凝土高墩桥抗震性能及经济性比较[J]. 公路, 2009(3): 48-51. SHEN Yonglin, MA Yuxian. Comparison of seismic performance and economic performance of normal concrete and lightweight concrete high pier bridges[J]. Highway, 2009(3): 48-51.

[6] 尹红亮. 轻质混凝土连续刚构桥地震响应分析[D]. 西安: 长安大学, 2011. YIN Hongliang. The seismic response analysis of lightweight concrete continuous rigid rrame bridge[D]. Xi’an: Chang’an University, 2011.

[7] 刘丽娟. 基于OpenSees的高强混凝土梁柱及框架的非线性有限元分析[D]. 合肥: 合肥工业大学, 2012. LIU Lijuan. Nonlinear finite element analysis of high-strength concrete beam column and frame based on opensees[D]. Hefei: Hefei University of Technology, 2012.

[8] 杨军平. 大震作用下考虑退化特性的RC框架结构抗整体性倒塌能力分析评估[D]. 兰州: 兰州理工大学, 2012. YANG Junping. Investigation on global collapse resistance of RC frame subjected to severe earthquake considering deterioration characteristic[D]. Lanzhou: Lanzhou University of Technology, 2012.

[9] 成文山, 邹银生, 程翔云. 钢筋混凝土压弯构件恢复力特性的研究[J]. 湖南大学学报, 1983, 10(4): 13-23. CHENG Wenshan, ZOU Yinsheng, CHENG Xiangyun. Research on the characteristics of restoring force for reinforced concrete members with flexure and axial force[J]. Journal of Hunan University, 1983, 10(4): 13- 23.

[10] 陈志强, 郑史雄, 陈志伟, 等. 高墩大跨连续刚构桥梁IDA分析结果离散原因[J]. 铁道科学与工程学报, 2018, 15(4): 962-969. CHEN Zhiqiang, ZHENG Shixiong, CHEN Zhiwei, et al. The cause of the discreteness of IDA analysis results for high pier and long span continuous rigid frame bridge[J]. Journal of Railway Science and Engineering, 2018, 15(4): 962-969.

[11] Lim J C, Ozbakkaloglu T. Stress–strain model for normal- and light-weight concretes under uniaxial and triaxial compression[J]. Construction and Building Materials, 2014, 71: 492-509.

[12] JGJ 12—2006, 轻骨料混凝土结构技术规程[S]. JGJ 12—2006, Technical specification for lightweight aggregate concrete structure[S].

[13] 王振宇,丁建彤, 郭玉顺. 结构轻骨料混凝土的应力-应变全曲线[J]. 混凝土, 2005(3): 39-41, 66. WANG Zhenyu, DING Jiantong, GUO Yushun. Stress-strain full curve of structural lightweight aggregate concrete[J]. Concrete, 2005(3): 39-41, 66.

[14] 陈桂斌, 王立成. 轻骨料混凝土应力-应变全曲线的数值模拟[J]. 建筑材料学报, 2008, 11(2): 138-143. CHEN Guibin, WANG Licheng. Numerical simulation on full compressive stress-strain curves of lightweight aggregate concrete[J]. Journal of Building Materials, 2008, 11(2): 138-143.

[15] Nielson B G, DesRoches R. Seismic fragility methodology for highway bridges using a component level approach[J]. Earthquake Engineering & Structural Dynamics, 2007, 36(6): 823-839.

[16] ZHANG Jian, HUO Yili. Evaluating effectiveness and optimum design of isolation devices for highway bridges using the fragility function method[J]. Engineering Structures, 2009, 31(8): 1648-1660.

[17] Pan Y, Agrawal A K, Ghosn M. Seismic fragility of continuous steel highway bridges in new york state[J]. Journal of Bridge Engineering, 2007, 12(6): 689-699.

[18] Cornell C A, Jalayer F, Hamburger R O, et al. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines[J]. Journal of Structural Engineering, 2002, 128(4): 526- 533.

[19] 吴文朋, 李立峰. 桥梁结构系统地震易损性分析方法研究[J]. 振动与冲击, 2018, 37(21): 273-280. WU Wenpeng, LI Lifeng. System seismic fragility analysis methods for bridge structures[J]. Journal of Vibration and Shock, 2018, 37(21): 273-280.

[20] 周长东, 王朋国, 田苗旺, 等. 多维地震下钢筋混凝土双曲线冷却塔结构易损性分析[J]. 振动与冲击, 2017, 36(23): 106-113, 151. ZHOU Changdong, WANG Pengguo, TIAN Miaowang, et al. Seismic vulnerability analysis for a RC hyperbolic cooling tower under multi-dimensional earthquakes[J]. Journal of Vibration and Shock, 2017, 36(23): 106-113, 151.

[21] 李宏男, 成虎, 王东升. 桥梁结构地震易损性研究进展述评[J]. 工程力学, 2018, 35(9): 1-16. LI Hongnan, CHENG Hu, WANG Dongsheng. A review of advances in seismic fragility research on bridge structures[J]. Engineering Mechanics, 2018, 35(9): 1-16.

[22] 陈志伟, 蒲黔辉, 李晰, 等. 行波效应对大跨连续刚构桥易损性影响分析[J]. 西南交通大学学报, 2017, 52(1): 23-29, 37. CHEN Zhiwei, PU Qianhui, LI Xi, et al. Fragility analysis of large-span continuous rigid bridge considering wave passage effect[J]. Journal of Southwest Jiaotong University, 2017, 52(1): 23-29, 37.

[23] 谢旭. 桥梁结构地震响应分析与抗震设计[M]. 北京: 人民交通出版社, 2006: 309-310. XIE Xu. Seismic response and earthquake resistant design of bridges[M]. Beijing: China Communications Press, 2006: 309-310.

Analysis of seismic vulnerability of lightweight aggregate concrete bridges

TAI Yuji1, HUI Yingxin1, SHI Xinhu2, JIN Baohong1, XU Zan1

(1. School of Civil Engineering and Hydraulic Engineering, Ningxia University, Yinchuan 750021, China;2. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China)

In order to improve the seismic performance of bridges in strong earthquake areas, lightweight aggregate concrete can be used to replace normal concrete to reduce the structural weight and improve the deformation capacity of the pier and column. It reduces the seismic response. Taking a typical medium and small span continuous beam bridge in a strong earthquake area as the research object, the finite element analysis model of lightweight aggregate concrete bridge was established based on OpenSees. Nonlinear time history analysis was carried out, and the seismic vulnerability curve was generated to evaluate the seismic performance of the bridge. The results show that compared with normal concrete bridges, the use of lightweight aggregate concrete for the upper structure or the lower structure is not obvious for reducing the overall damage of the bridge. Lightweight aggregate concrete bridges in the whole bridge can significantly reduce the damage probability of bridge piers, pile foundations and supports, and the overall damage probability of bridges. It is recommended that when constructing bridges in strong earthquake areas, the whole bridges use lightweight aggregate concrete instead of normal concrete to improve the seismic performance of the bridge.

bridge engineering; lightweight aggregate concrete; seismic vulnerability; probabilistic seismic demand model; first-order boundary method

10.19713/j.cnki.43-1423/u.T20190235

U448

A

1672 - 7029(2020)01 - 0129 - 10

2019-03-28

宁夏高等学校优青培育基金资助项目(NGY2017005)；国家自然科学基金资助项目(51608283)

惠迎新(1985-)，男，内蒙古阿拉善盟人，副教授，博士，从事桥梁抗震研究； E-mail：huiyx@seu.edu.cn

(编辑 阳丽霞)