考虑高铁客运产品间交叉弹性的动态票价策略

车瑶，符卓，袁雪莹

考虑高铁客运产品间交叉弹性的动态票价策略

车瑶，符卓，袁雪莹

(中南大学 交通运输工程学院，湖南 长沙 410075)

将由特定高铁列车所提供的起讫点间的旅客运输服务定义为单个高铁客运产品。随着高速铁路越来越“公交化”，同一起讫点间客运产品间的可替代性越来越强，票价的调整有了更精细化的要求。用经济学中的交叉弹性理论描述客运产品间的可替代程度，用指数需求函数描述客运产品的需求与票价的关系，构建并求解高铁动态票价优化模型，对客运产品间不同可替代程度下的最优动态票价策略进行研究。结果显示：高铁客运产品间的可替代性会影响票价策略的选择，且客运产品间可替代程度的增加是否有利于客票收益的提高与可行折扣票价集合的选取有关。

高速铁路；旅客运输；可替代程度；交叉价格弹性；动态定价

目前，固定单一的票价体系已经很难适应市场经济的需要和动态的旅客需求，不利于高铁运营企业提高自身的经济效益。铁路总公司目前正在不断推进铁路市场化改革，暨2017年4月对东南沿海高铁进行第1次跨省调价后，又公布从2019年4月19日起到“五一”小长假之前对海南环岛高铁及江湛铁路部分动车组列车实行浮动票价。近些年，来高速铁路发展迅速，运行组织模式越来越“公交化”，同一区段列车间的可替代性越来越强，市场化改革体制下高速列车的票价可以根据客流状况上下浮动，这使得高铁票价有了更多可优化的方向。高铁客运需求弹性是指高铁客运的需求对于其影响因素变化做出反应的敏感程度，可以描述需求与票价的变化关系。因此，本文基于客运需求弹性探讨考虑客运产品间可替代性的高铁动态票价优化问题，以提高高铁运营企业的客票收益。目前，除了将经济学中的需求弹性理论应用于产品自身的需求弹性分析外[1-3]，还有诸多学者将经济学中的交叉弹性理论应用于产品间可替代性的分析。在交通运输领域，李文君等[4]通过实际运营数据测算和分析高速铁路对公路的交叉速度弹性和交叉价格弹性；陈伯阳等[5]考虑公交与其他交通方式之间的竞争，对实际运营数据进行分析，得到公交与其他交通方式之间的交叉弹性值。在其他经济领域，王维等[6]利用Logistic方程分析交叉弹性对企业知识共享行为的作用和影响，结果表明当交叉弹性值维持在一定范围内时，2企业会摆脱“囚徒困境”，选择知识共享。高铁动态票价优化问题可以分为单列车动态票价优化问题[7-8]和多列车动态票价优化问题，其区别在于多列车动态票价优化问题考虑列车间的可替代性。多列车动态票价优化问题属于多产品动态定价问题。CHEN等[9]考虑客户需求的转移影响，研究可替代产品的动态定价问题，并利用多项式时间近似方法对动态规划算法进行优化；刘海英等[10]研究考虑记忆窗口的多产品动态定价问题，研究结果表明：从长期来看，企业收益不仅与初始价格有关，还与客户记忆窗口的长度有关。诸多学者将多产品动态定价理论应用于交通运输领域，ZHANG等[11]针对同一OD间多个航班的动态票价优化问题，建立基于剩余座位数和票价的动态规划模型，并对定价策略进行分析。李博等[12]研究同一OD对间可替代较强的2趟高铁列车的动态票价优化问题，建立离散时间的动态规划模型，分析2列车的最优定价与预售时间、剩余座位数之间的关系。在铁路运输领域，学者多从整个高铁市场的角度出发，将交叉弹性理论用于分析不同交通方式间的可替代性，对铁路客票价格的调整起到了参考作用。随着高铁越来越“公交化”，同一区段提供的运输服务间的可替代性越来越强，但少有文献对高铁内部运输服务间的可替代性进行分析。并且已有文献在探讨高铁动态票价优化问题时，虽然有考虑到不同客运产品间的可替代性，但少有文献对客运产品间可替代程度的大小与动态票价策略的关系进行分析。因此，本文将经济学中的交叉弹性理论应用于高铁内部运输服务中，探讨考虑客运产品间可替代程度大小的高铁动态票价策略制定问题。

1 问题描述

从微观的角度出发对高铁内部运输服务的可替代程度进行描述和测算。考虑客运产品间的可替代性，客运产品会互相受到某些因素变化的影响。本文要探讨的是考虑高铁客运产品间可替代性的动态票价策略，因此仅考虑价格因素变化的影响。

交叉价格弹性的定义为一种可替代的运输服务的价格每变动1%将引起的另一种可被替代的运输服务的需求量变化的百分比。客运产品提供的服务也是运输服务的一种，因此，若将定义中的运输服务换为客运产品，该定义依然成立。设有2种高铁客运产品和，则用弧弹性中点公式计算客运产品对客运产品的交叉价格弹性的表达式如式(1)所示；由于客运产品对客运产品的交叉价格弹性即为客运产品的需求价格弹性，则客运产品的需求价格弹性也可用式(1)计算：

若客运产品对客运产品的交叉价格弹性值大于0，说明的价格变动使得的需求同方向变动，说明对来说，具有可替代性。

2 模型构建

在构建高铁动态票价优化模型前，根据本文的研究背景，首先对旅客需求的特性做如下假设：

1) 各OD对之间的需求相互独立，某个OD的票价发生变化，其他OD的需求不会受到影响；

2) 铁路企业能够完全掌握客运产品的需求信息，客运产品的需求为确定型需求。

考虑到同一区段间的客运产品具有可替代性和不同预售期客运产品的需求对票价变化做出反应的敏感程度不同的情况，本节构建高铁动态票价优化模型。其中“动态”是相对于传统的“差异化”定价而言，即票价会随着预售时间的推移而变化。

2.1 需求函数

定义单位时间内的购票旅客数量为需求密度，用()表示，则在独立确定型需求的假设下，客运产品的服务属性没有变化时，其需求只与自身价格相关。本文对票价优化的思路是在基础票价上进行上下浮动从而得到优化票价，采用经济学研究中普遍使用的指数需求函数来描述需求和票价的关系，一般表达式如式(2)所示：

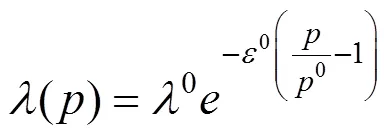
式中：表示产品的价格；0表示基础价格；0是基础价格下的需求密度；0是产品在基础价格下的需求价格弹性绝对值。

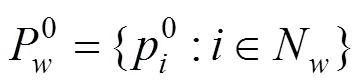
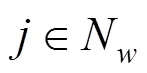
由于客运产品对客运产品的交叉价格弹性即为客运产品的需求价格弹性，则式(3)可以简化为式(4)：

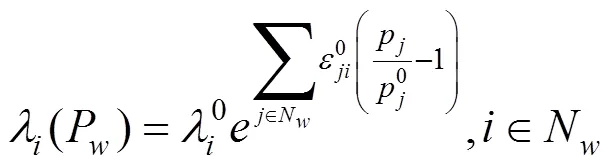
2.2 模型建立

2.2.1 分阶段

研究根据客运产品的需求特性制定调价决策。在非节假日时，出行确定性高的旅客例如学生、游客会提前很久购票，这些旅客对票价会比较敏感，而出行不确定性高的旅客例如商务人员一般倾向于当天或提前几天购票，这些旅客对票价不太敏感。因此，旅客预售期购票规律曲线中需求突变的时间点可以作为划分旅客在客票预售期上的分布情况的依据。由此可知，若将需求突变时间点作为划分预售期的依据，则可使得同一个阶段内的旅客对票价变化做出反应的敏感程度比较统一，从而可将客运产品的预售期划分为T个阶段。用=1,…,T表示阶段，其中=1表示预售期初始阶段，=T表示客运产品的最后一个阶段。用d,i表示客运产品的第个阶段的时间长度。

2.2.2 决策变量

2.2.3 售票数

2.2.4 目标函数

在客票预售期已经被划分为不同阶段的基础上，以整个预售期所有高铁客运产品的总收益最大为目标得到目标函数的表达式如式(6)所示：

2.2.5 售票数约束

本文探讨的是客运产品间不同可替代程度大小下的动态票价策略，而在求解模型过程中，由于售票数约束条件的限制可能会导致最优票价策略被筛选掉，影响本文的分析结果。因此，本文假设资源充足，不对客运产品的售票数进行限制。

2.2.6 票价取值约束

本文用离散时间动态定价模型对动态票价问题进行分析，则用离散的可行票价集合D来约束客运产品的票价取值范围，票价取值约束条件如式(7)所示：

3 算例分析

以A，B和C 3站间运行的2趟列车G1和G2为例(图1)进行算例分析。图1中有4个客运产品，分别为G1+AB(=1)，G1+BC(=2)，G1+AC(=3)和G2+AC(=4)，记为客运产品1，2，3和4。

图1 G1和G2列车示意图

为了使各参数的取值更接近实际情况，本文按如下规定对参数进行取值。

1) 考虑到客运产品G2+AC为直达客运产品，往往会更受旅客的欢迎，设定其各阶段的需求密度均大于客运产品G1+AC。

2) 考虑到存在可替代产品的区段间的旅客会更倾向于晚购票，设定客运产品G1+AC和G2+AC第1阶段的长度大于其他客运产品第一阶段的 长度。

3) 考虑到当距离发车时间较长时，旅客的出行规划不确定性高，对票价的变动更敏感。设定距离发车时间越长的阶段的需求价格弹性和交叉价格弹性越大。

4) 客运产品G1+AB和G1+BC的区段长度小于客运产品G1+AC和G2+AC，考虑到距离越长，票价越高，在相同票价折扣下，旅客对票价变动的敏感程度越高，设定客运产品G1+AB和G1+BC的需求价格弹性小于客运产品G1+AC和G2+AC的需求价格弹性。

5) 所有客运产品中只有客运产品G1+AC和G2+AC间存在可替代性，考虑到直达客运产品会更受欢迎，设定客运产品G2+AC对G1+AC的交叉价格弹性(客运产品G2+AC的需求对客运产品G1+AC票价变化的敏感程度)小于客运产品G1+AC对G2+AC的交叉价格弹性。

以所有高铁客运产品的实际票价为基础，则所有高铁客运产品的基础票价折扣方案为1。采用matlab2018a编程求解本文所建模型。

本文给出的算例中客运产品1和2均不存在可替代产品，2客运产品的交叉价格弹性值均为0，因此，客运产品3和4的交叉价格弹性值的大小便可表示整体高铁客运产品间的可替代程度。记算例中交叉价格弹性值所表示的可替代程度的大小为程度3，算例中交叉价格弹性值的一半所表示的可替代程度的大小为程度2，交叉价格弹性值为0(即客运产品间不具有可替代性)所表示的可替代程度的大小为程度1。数字越大，代表可替代程度越高。则客运产品间的交叉价格弹性值与可替代程度值的对应情况如表1所示。

在资源充足和其他参数取值不变的情况下，求解不同可行折扣票价集合下客运产品不同可替代程度情况下的最优票价策略，结果如表2和表3 所示。

表1 客运产品间的交叉价格弹性值与可替代程度值的对应情况

表2 可行折扣票价集合为(1.0,0.9,0.8)时不同可替代程度下的最优票价策略

从表2中的结果可以看出：随着客运产品间可替代程度的增强，最优票价策略出现变动，且最优票价策略对应的总收益在减少，可以得出在本文给出的3个可替代程度等级下当可行折扣票价集合为(1.0,0.9,0.8)时，客运产品间的可替代程度越小，选择最优票价策略所能获得的总收益越大。

表3 可行折扣票价集合为(1.1,1.0,0.9)时不同可替代程度下的最优票价策略

从表3中的结果可以看出：随着客运产品间可替代程度的增强，最优票价策略出现变动，且最优票价策略对应的总收益先减小后增大，可以得出在本文给出的3个可替代程度等级下当可行折扣票价集合为(1.1,1.0,0.9)时，随着客运产品间可替代程度的增加，选择最优票价策略所能获得的总收益先减小后增加。

当客运产品间的可替代程度为1时，对比表2和表3中总收益列的第1行的数据可知，选取可行折扣票价集合(1.0,0.9,0.8)时最优票价策略对应的总收益更大；当客运产品间的可替代程度为2和3时，对比表2和表3中总收益列的第2行和第3行的数据可知，此时选取可行折扣票价集合(1.1,1.0,0.9)时最优票价策略对应的总收益更大。

根据以上分析可以得出：客运产品间可替代程度的增强是否有利于客票收益的提高与可行票价折扣集合的选取有很密切的关系。因此，在高铁越来越“公交化”的现实背景下，高铁企业在制定票价策略时应对客运产品间的可替代性及其可替代程度进行分析，充分利用客运产品间的可替代性，制定合理的票价策略和可行折扣票价集合，以提高高铁运营部门的客票收益。

4 结论

1) 考虑客运产品间存在的可替代性，将经济学中的交叉弹性理论应用于高铁内部运输服务中，对如何测算高铁客运产品间的可替代程度进行描述，构建并求解高铁动态票价优化模型，得到客运产品间不同可替代程度下的高铁动态票价策略。

2) 本文构造的算例验证了客运产品间的可替代性会影响动态票价策略的制定，且其是否有利于客票收益的提高与可行票价集合的选取有关，今后可以依据本文构建的模型分析大算例下客运产品间的可替代性与动态票价策略的关系。

3) 今后考虑构造大算例，从以下2个角度出发做进一步研究：1) 根据客运产品的可替代情况和预售期规律对客运产品进行归类，减小算例的规模；2) 针对大算例，构造智能优化算法进行求解。

[1] Givoni M. Development and impact of the modern high-speed train: A review[J]. Transport Reviews, 2006, 26(5): 593-611.

[2] Martijn Brons, Eric Pels, Peter Nijkamp, et al. Air travel demand elasticity concept issues and measurement[D]. Waterloo, ON, Canada: University of Waterloo, 2002.

[3] 韦涛. 铁路客票销售策略的需求弹性控制方法研究[J]. 铁道运输与经济, 2018, 40(12): 24-28, 92. WEI Tao. A research on demand elasticity control method of ticketing strategy for railway passenger transport[J]. Railway Transport and Economy, 2018, 40(12): 24-28, 92.

[4] 李文君, 符卓. 高速铁路客运需求弹性分析[J]. 铁道科学与工程学报, 2016, 13(11): 2115-2124. LI Wenjun, FU Zhuo. Elasticity analysis for high-speed railway passenger transport demand[J]. Journal of Railway Science and Engineering, 2016, 13(11): 2115- 2124.

[5] 陈伯阳, 蒋明清, 四兵锋, 等. 多方式竞争下城市公交需求价格弹性实证分析[J]. 交通运输系统工程与信息, 2016, 16(4): 241-247. CHEN Boyang, JIANG Mingqing, SI Bingfeng, et al. Empirical analysis of demand-price elasticity for urban public transit in multimodal transport system[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(4): 241-247.

[6] 王维, 周鹏. 考虑需求交叉弹性的企业知识共享行为分析——基于集群创新网络环境[J]. 科技进步与对策, 2013, 30(20):128-132. WANG Wei, ZHOU Peng. A behavior analysis of enterprise knowledge sharing under the cross elasticity of demand--based on cluster innovation network[J]. Science & Technology Progress and Policy, 2013, 30(20): 128- 132.

[7] 史峰, 郑国华, 谷强. 铁路客票最优动态票价理论研究[J]. 铁道学报, 2002, 24(1): 1-4. SHI Feng, ZHENG Guohua, GU Qiang. Optimal dynamic pricing of railway passenger ticket[J]. Journal of the China Railway Society, 2002, 24(1): 1-4.

[8] 宋文波, 赵鹏, 李博, 等. 高速铁路动态定价的稳健优化模型[J]. 哈尔滨工业大学学报, 2018, 50(9): 25-30. SONG Wenbo, ZHAO Peng, LI Bo, et al. Robust optimization model of dynamic pricing for high-speed railway[J]. Journal of Harbin Institute of Technology, 2018, 50(9): 25-30.

[9] CHEN Shaoxiang, Gallego G, Li M Z F, et al. Optimal seat allocation for two-flight problems with a flexible demand segment[J]. European Journal of Operational Research, 2010, 201(3): 897-908.

[10] 刘海英, 罗新星, 邓丽. 基于记忆窗口与参照效用的多产品动态定价[J]. 系统工程, 2016, 34(5): 36-42. LIU Haiying, LUO Xinxing, DENG Li. Multi-product dynamic pricing based on customers' memory window and reference effects[J]. Systems Engineering, 2016, 34(5): 36-42.

[11] ZHANG Dan, Cooper W L. Pricing substitutable flights in airline revenue management[J]. European Journal of Operational Research, 2009, 197(3): 848-861.

[12] 李博, 赵鹏, 李云峰, 等. 基于旅客分类的高速铁路平行车次动态定价研究[J]. 铁道学报, 2017, 39(9): 10-16. LI Bo, ZHAO Peng, LI Yunfeng, et al. Research on dynamic pricing of parallel trains of high-speed railway based on passenger segment[J]. Journal of the China Railway Society, 2017, 39(9): 10-16.

Dynamic ticket price strategy considering the degree of cross price elasticity between high-speed railway passenger products

CHE Yao, FU Zhuo, YUAN Xueying

(School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)

In this paper, the passenger transport service between origin and destination provided by a specific high-speed train is defined as a single high-speed passenger transport product. As the high-speed railway becomes more and more “public transportation”, the substitutability between passenger products of the same OD becomes stronger and stronger, and the adjustment of pricing has more refined requirements. In this paper, the cross-elasticity theory in economics was applied to the internal transport service of high-speed railway to analyze the degree of substitution and the relationship between ticket price and demand was described by Log-Linear function. A fare optimization model for multi-passenger products was established and solved. The choice of optimal fare strategy under different substitutability was studied. The results show that the substitutability between passenger transport products will affect the formulation of fare strategy, and whether its increase is conducive to the increase of passenger ticket revenue is related to the selection of feasible fare discount set.

high-speed railway; passenger transportation; the degree of substitution; cross price elasticity; dynamic pricing

10.19713/j.cnki.43-1423/u. T20190434

U293

A

1672 - 7029(2020)01 - 0025 - 06

2019-05-21

国家自然科学基金高铁联合基金资助项目(U1334207)；国家自然科学基金资助项目(71271220)

符卓(1960-)，男，海南文昌人，教授，从事交通运输规划与管理等研究；E-mail：zhfu@csu.edu.cn

(编辑 阳丽霞)