基于有限元仿真的列车-桥梁防护墙碰撞研究

吕思雨，钟睦，鲁寨军，刘项

基于有限元仿真的列车-桥梁防护墙碰撞研究

吕思雨1, 2, 3，钟睦1, 2, 3，鲁寨军1, 2, 3，刘项1, 2, 3

(1. 轨道交通安全教育部重点实验室，湖南 长沙 410075；2. 轨道交通安全关键技术国际合作联合实验室，湖南 长沙 410075；3. 轨道交通列车安全保障技术国家地方联合工程研究中心，湖南 长沙 410075)

针对桥梁防护墙防护能力研究较为匮乏的现状，基于有限元理论，运用Hypermesh软件建立有砟无砟轨道桥梁上动车组头车与防护墙碰撞的有限元模型，采用数值仿真方法对动车组头车碰撞防护墙过程进行分析和研究，获得不同速度和不同冲角碰撞工况下防护墙的受力与变形及列车运行轨迹的变化。研究结果表明：动车组头车以较低速度、较小冲角碰撞防护墙时，防护墙受损破坏程度较轻；当碰撞速度较高、冲角较大时，防护墙受损程度较重，头车有轻微爬墙现象。加高防护墙后建立相关工况下的碰撞模型进行仿真计算，通过分析其碰撞过程和碰撞力、头车偏转角及速度随时间的变化情况，发现增高后的防护墙能有效抑制列车爬墙现象，列车运行稳定性较好。

动车组；防护墙；有限元仿真；碰撞过程

动车组列车在为人们生活提供便捷，大大加速国民经济发展的同时，也会出现列车脱轨事故，这对铁路列车的运行安全性提出了严峻的考验[1]。列车若在桥面上脱轨，可能导致车厢坠落甚至砸伤地面行人，损失较为严重。国内外针对各自规范制定了安全限度标准，并根据各自国情采取不同的安全防护措施[2]：法国采用有砟道床，安装护轮轨防止列车脱轨后冲出桥面；瑞典通过加高挡砟墙来降低列车脱轨后坠桥的几率；德国主要采用电缆槽墙体作为列车的安全防护措施，并增设混凝土挡块防止列车脱轨后冲出轨道过远；日本则采用在车体上安装反L型车辆导向装置并在轨道两侧设立护轮轨的方式。我国在客货共线铁路桥梁设计中提出要设置防护墙，在防护墙设计过程中，需考虑列车脱轨后对防护墙的撞击力，目前，作用在防撞墙上的荷载按与轨顶面平齐，横向200 kN/m考虑。由于列车脱轨问题本身的复杂性和极端性，目前还没有关于桥梁上脱轨列车—防护墙碰撞过程的实车试验，故采用理论推导和数值仿真的方法评价桥梁防护墙的防撞性能。在理论推导方面，向俊等[3−5]推导出高速铁路桥梁防撞墙受力计算公式，计算出脱轨摇摆力为630 kN，防撞墙所受到的撞击力为33 002.4 kN，但理论推导简化了很多条件，不够贴合实际。在数值仿真方面，毕继红等[6−8]基于ANSYS/ LSDYNA显式动力算法的仿真分析模拟磁悬浮列车擦撞并侵入混凝土护栏，最终导致护栏局部失效散裂的破坏效应，且撞击角度越大，护栏的破坏程度越严重，但其用质量块代替列车进行仿真，无法研究列车碰撞后的运行状态。相比于碰撞试验，列车的碰撞仿真克服了费用高昂、测试周期漫长、可重复性差和不可控因素多等缺点，且可获得更多的数据，具有较高的经济性和可行性[9−11]。关于脱轨后的车辆与防护墙发生碰撞的仿真分析，在汽车领域已开展了不少研究，但在铁道领域，还很少有人对此进行研究[12−13]。在此，本文基于铁路列车脱轨行为，对铁路列车脱轨后与轨道防护措施碰撞过程进行建模仿真分析，进而对桥梁脱轨防护措施的防护性能进行评估。

1 动车组与防护墙碰撞初始条件假定

动车组脱轨后与桥梁防护墙碰撞是一个较为复杂的过程，整个过程分为“脱离轨道并掉落”、“继续行驶”和“碰撞”3个阶段，其中“碰撞”过程为本文研究对象。为方便建模及计算，对前2个阶段进行简化，动车组受重力掉落至道砟，沿脱轨速度方向继续行驶，继续行驶时受到道砟的摩擦速度降低。

1.1 动车组及桥面结构的确定

选用我国客货共线铁路上具有代表性的某型号动车组作为研究对象，其头车模型如图1所示。该动车组运营时速为200 km，头车模型由车辆与2个转向架组装构成，动车组头车模型总长25 000 mm，高3 700 mm，宽3 370 mm，总质量为54.058 t，单个转向架质量为6.625 t。

图1 动车组头车几何模型

根据所选用动车组，参考时速200 km客货共线铁路有砟桥面预应力混凝土双线整孔简支箱梁通用参考图，选择有砟轨道直线梁作为后期整体建模的桥梁参考图。根据参考图中相关尺寸可知，防护墙距离轨道中心线2 285 mm，由此确定防护墙的具体位置，防护墙厚度为200 mm，防护墙高1 050 mm，轨顶所在平面距离防护墙底端约710 mm，因此防护墙最终高出道砟340 mm，整体示意如图2所示。

1.2 碰撞速度及冲角的确定

根据该动车组实际运营情况，本文选取碰撞速度80，120和200 km/h的工况进行研究。

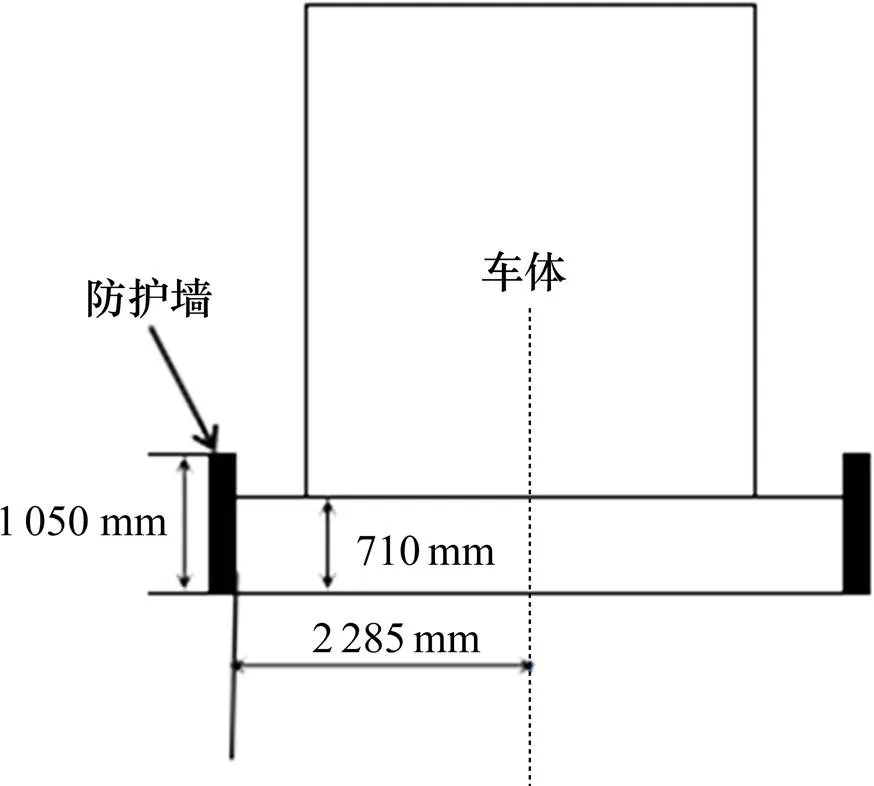
图2 防护墙断面示意图

图3 脱轨冲角示意图

2 车体−防护墙有限元模型的建立

有限元模型对数值模拟计算结果有很大影响，其中2个重要元素分别为有限元模型与实物的近似程度和网格的大小、数目及形状。数值模拟所分析得到的结果精度、可靠性以及计算成本均取决于有限元模型。本文选用Hypermesh软件划分网格、设置相关参数。

2.1 有限元模型及网格划分

由于动车组头车在脱轨后需继续前进一定时间后才能与防护墙发生碰撞，为节约计算成本，将列车沿线路脱轨处平移至与防护墙较为接近的位置，并对动车组−桥梁有限元模型进行相应简化。网格密度是关系整车碰撞计算仿真的精度和效率的重要因素，密度过小会降低计算效率，密度过大则会降低计算精度。为得到比较精确的结果，转向架、排障器、设备舱等易碰撞部位网格单元尺寸取为50 mm，其他取为100 mm。划分网格后，列车−桥梁防护墙碰撞的有限元模型如图4所示，动车 组头车模型中单元数为119 317，节点(Node)数为 117 500。

图4 列车−防护墙简化有限元模型示意图

2.2 材料参数

车体主要由铝合金构成，主要涉及的材料参数如表1所示。

表1 动车组用铝合金材料参数

防护墙主要由混凝土材料构成，在仿真过程中，车辆以较高的速度撞向防护墙，可以将其认为是混凝土结构受到压缩甚至发生侵彻的问题。经查阅资料，并对初步仿真模拟结果进行分析和对比，确定混凝土的材料采用MAT72R3模型，其主要应用于高应变率、大变形下的混凝土与岩石模拟，采用该模型进行仿真得到的结果可靠性更强。该模型只需设置表2所示参数，其他参数由其内部程序自动计算。

表2 防护墙用混凝土材料参数

由于本文重点研究防护墙的防撞性能，因此为便于计算，将道床假设为刚性墙，采用MAT20材料模型。

2.3 接触及边界条件

对防护墙墙体底端和地面建立全自由度约束，对车体施加重力加速度。参考相关文献[14−15]，轮轨之间的静摩擦因数设置为0.3，动摩擦因数设置为0.05。车与防护墙碰撞后会擦撞前行，因此也需考虑车与墙之间的摩擦力，车墙之间的静摩擦因数设置为0.3，动摩擦因数设置为0.15。在车轮与桥面之间、车体与防护墙之间建立接触，接触类型为自动面面接触(Automatic Surface to Surface)。

3 现有防护墙碰撞结果分析

碰撞初始条件的不同主要体现在碰撞速度和冲角的不同，分别设置碰撞速度为80，120和200 km/h，在不同冲角下建立有限元模型进行仿真。

3.1 80 km/h速度级下碰撞结果

图5为碰撞速度为80 km/h时各冲角的碰撞力随时间变化的情况。不同冲角下曲线趋势大致一致，在碰撞过程中均出现了2次峰值力，第1次峰值力是由于动车组头车头部直接碰撞导致，第2次峰值力是由于在列车的“甩尾”作用下头车尾部碰撞导致，在2次峰值力之间，由于头车向前固有的运动趋势导致动车组与防护墙上端发生持续的擦撞，防护墙上端部位产生了一定程度的破损。

图5 碰撞时速80 km时不同冲角下碰撞力−时间曲线

图6为碰撞速度为80 km/h时各冲角的2次峰值力。碰撞过程中的峰值力随冲角增大而变大，当冲角达到1.5°时，碰撞力峰值增大明显，头车直接碰撞产生的峰值力约为1.0°冲角工况中峰值力的1.25倍，之后其增长幅度变缓。第2次峰值力均大于第1次，说明列车“甩尾”作用产生了较大的力。

图6 碰撞时速80 km时不同冲角下碰撞力峰值

图7为碰撞速度为80 km/h时各冲角下头车偏转角随时间的变化情况，头车偏转角度指头车与防护墙发生碰撞后其运行方向偏离脱轨时运行方向的角度。由图7可知，随碰撞时间的增长，头车偏转角变大，说明动车组头车由于受到防护墙横向撞击力，与防护墙分离并发生一定程度向轨道内侧的偏转。当头车偏转角等于其脱轨冲角时，说明头车运行方向已摆正。在计算终止时刻，1.0°冲角工况下的头车偏转角为0.91°，1.5°冲角工况下的头车偏转角为1.54°，2.0°冲角工况下的头车偏转角为2.15°，2.5°冲角工况下的头车偏转角为2.51°，故头车方向已大致摆正。因此防护墙在计算时间内已将脱轨头车完全推离，动车组头车与防护墙碰撞后贴着防护墙继续前行。

图7 时速80 km不同冲角下头车偏转角−时间曲线

3.2 120 km/h及200 km/h速度级下碰撞结果

对120 km/h及200 km/h速度级动车组头车进行有限元仿真，从车体受力云图可知碰撞主要集中在图8所标示部位，其中部位1为排障器，部位2为设备舱端部。冲角为1.0°和1.5°时，部位2碰撞防护墙；冲角为2.0°和2.5°时，部位1和部位2同时碰撞防护墙。部位1 和部位2的共同特点是比较尖锐，因此车体以较高速度冲向防护墙时，碰撞产生的力较大，墙体最上层单元被其侵蚀，不利于防护脱轨列车，且防护墙上端被碰撞后损坏导致防护墙变矮，列车设备舱底部有爬墙趋势，但仍能对脱轨列车发挥限位导向作用。

分析碰撞时速为120 km和200 km时各工况下各方向碰撞力随时间的变化可知：碰撞发生初期，车体对防护墙的垂向撞击力占主导，随后总碰撞力主要来自车体对防护墙向前的推力。选取时速200 km，冲角2.0°工况进行说明，防护墙受力情况如图9所示，其中Resultant force指碰撞总力，-force指沿防护墙向前的作用力，-force指垂直于防护墙侧面的作用力，-force指沿防护墙向下的作用力，图中分别给出了碰撞力上升时刻及下降时刻的受力云图。由图9可知，碰撞初期的力主要来自与车体对防护墙的垂向冲击(即-force)；此后由于部位2结构的特殊性，在豁口处对防护墙产生向前的推力(即-force)，该力增大明显，并成为碰撞总力的主要来源；设备舱端部底板有轻微爬墙趋势，对防护墙向下的作用力(即-force)逐渐增大，此时防护墙破损程度较为严重。

图10为碰撞时速为120 km和200 km时各冲角下动车组头部直接碰撞防护墙产生的峰值力(即第1次峰值力)，碰撞速度相等时，碰撞力随冲角的增大而增大，200 km/h速度级下的碰撞力远大于120 km/h速度级下的碰撞力，因此碰撞速度越高、冲角越大，碰撞导致的危险系数就越高。

图8 车体主要碰撞部位

图9 时速200 km冲角2.0°防护墙受力情况

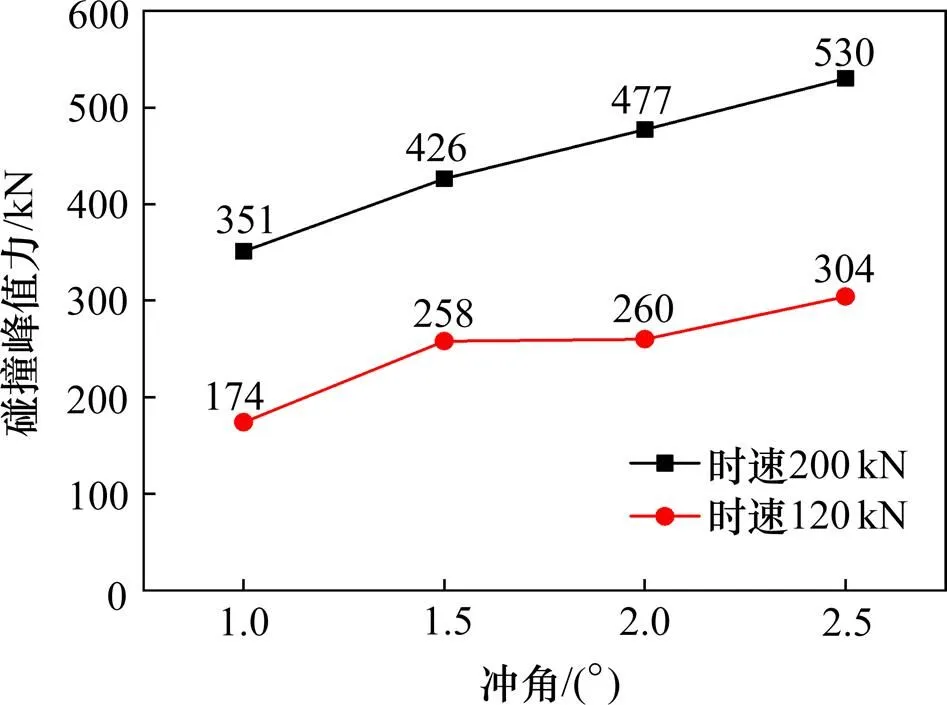
图10 各工况下碰撞力峰值

3.3 防护墙防护性能评估及优化方案

通过对碰撞仿真的结果进行分析可知，碰撞速度为80 km/h时，防护墙有较好的防护导向作用；碰撞速度达到120 km/h时，由于防护墙上层单元被尖锐的设备舱端部侵蚀导致其被严重破损而变矮，动车组的设备舱底部易出现爬墙趋势，从而影响行车稳定。

防护墙高度的改变可直接影响头车与防护墙的碰撞位置，车体不同位置处结构不同，碰撞过程也有所差异，设备舱端部和排障器的边缘位置碰撞刚度较弱且设备舱在此碰撞位置下容易出现爬墙趋势，因而危险系数较大。将防护墙高度增高至超过设备舱端部，则可避免动车组尖锐部位对防护墙的碰撞，减轻撞击对墙的损坏。

4 加高防护墙后碰撞结果分析

将原始高度为1 050 mm的防护墙增高至超过设备舱端部，取其高度为1 390 mm，则防护墙高出道砟的高度由340 mm变为680 mm。加高防护墙后研究200 km/h 速度级下碰撞过程，建立有限元模型并进行仿真计算。

4.1 防护墙受力分析

碰撞时速为200 km时，加高防护墙后不同冲角下动车组头车与防护墙的碰撞力随时间变化的趋势如图11所示，其碰撞力峰值如图12所示。车体在计算时间内出现2次峰值力，且冲角低于2.5°工况中，车体“甩尾”产生的峰值力略大于头车冲撞防护墙产生的峰值力，但冲角为2.5°时，第2次峰值力明显大于第1次峰值力，约为第1次峰值力的1.33倍。冲角低于2.5°时碰撞力较小，但在2.5°时碰撞力峰值增大明显，说明冲角大于2.0°后，碰撞强度增大明显，故冲角达到一定程度后碰撞危险系数明显增高。

图11 碰撞时速200 km不同冲角下碰撞力−时间曲线

选取时速200 km，冲角2.0°工况对加高后的防护墙进行受力分析，与原始高度防护墙的受力情况进行对比，其总碰撞力和各方向碰撞力如图13所示。由图13可知，加高防护墙后垂直于防护墙的力(-force)与总碰撞力(resultant force)随时间变化的趋势一致且占总碰撞力的主体，说明碰撞主要来自于列车对防护墙的垂向撞击，而其他方向的力较小，加高防护墙后可有效避免设备舱端部对防护墙的纵向推撞，因而可减轻防护墙的损坏程度。防护墙高度的增高改变了动车组与防护墙的接触位置，增高后的防护墙能更好地发挥限位导向作用。

图12 碰撞时速200 km不同冲角下碰撞力峰值

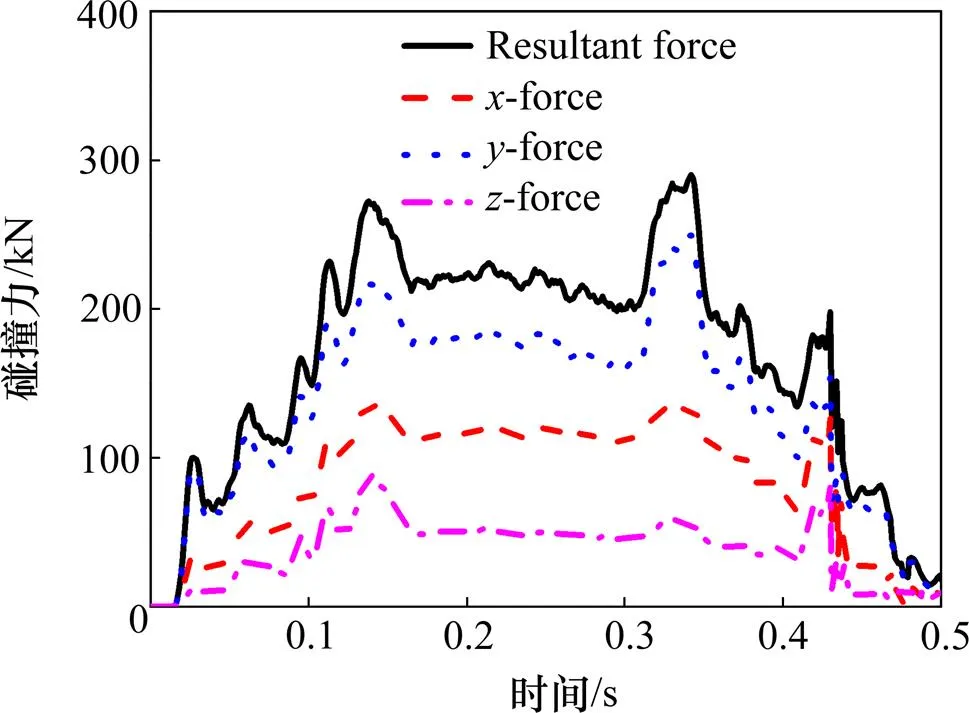
图13 加高防护墙后时速200 km冲角2.0°防护墙受力情况

4.2 动车组运行姿态分析

图14为碰撞时速200 km时不同冲角下头车偏转角随时间的变化情况，在计算时刻为0.46 s左右，1.0°冲角、1.5°冲角和2.0°冲角工况下的头车方向已摆正，在计算时刻为0.49 s左右，2.5°冲角工况下的头车方向已摆正，说明防护墙在计算时间内已将脱轨头车完全推离，动车组头车与防护墙碰撞后贴着防护墙继续前行。

图14 时速200 km不同冲角下头车偏转角−时间曲线

5 结论

1) 基于Hypermesh/Ls-dyna建立某型号动车组头车与现用时速 200 km客货共线铁路有砟桥面防护墙的有限元模型，模拟列车脱轨后与防护墙碰撞的整个过程。通过计算结果可知，列车脱轨后先碰撞防护墙，在“甩尾”作用下前后发生两次碰撞且第二次峰值更大，之后沿防护墙继续向前行驶，防护墙能够起到限位和导向的作用，减少了列车脱轨后坠桥的几率。

2) 碰撞危险系数随动车组碰撞速度和冲角的增大而变高，碰撞速度达到120 km/h时，防护墙破损情况严重，动车组会出现轻微爬墙现象，但仍能对脱轨列车起到限位和导向作用。

3) 加高防护墙后再次进行碰撞仿真计算，由于车体碰撞部位的改变，车体不易出现爬墙现象，防护墙破损程度减轻，动车组与防护墙碰撞后沿防护墙擦撞前行，防护墙能更好地发挥限位导向作用，列车碰撞后的运行安全性有所提高。

[1] 王文斌, 康康, 赵洪伦. 列车耐碰撞系统有限元和多体动力学联合仿真[J]. 同济大学学报(自然科学版), 2011, 39(10): 1552−1556. WANG Wenbin, KANG Kang, ZHAO Honglun. Joint simulation of crashworthy train set based on finite element and multi-body dynamic[J]. Journal of Tongji University (Natural Science), 2011, 39(10): 1552−1556.

[2] 肖沁凯. 高速铁路桥梁安全防护措施分析[J]. 铁道标准设计, 2010(6): 70−72. XIAO Qinkai. Analysis on safety protection measures of high-speed railway bridges[J]. Railway Standard Design, 2010(6): 70−72.

[3] 向俊, 龚凯, 毛建红, 等. 高速列车运行安全性与桥梁防撞墙受力分析[J]. 铁道学报, 2011, 33(12): 83−87. XIANG Jun, GONG Kai, MAO Jianhong, et al. Analysis on the running safety of high-speed train and the force of bridge collision-proof wall[J]. Journal of the China Railway Society, 2011, 33(12): 83−87.

[4] 向俊, 曹晔, 刘保钢, 等. 客运专线板式无碴轨道动力设计参数[J]. 中南大学学报(自然科学版), 2007, 38(5): 981−986. XIANG Jun, CAO Ye, LIU Baogang, et al. Dynamic parameters of slab track of passenger transport line[J]. Journal of Central South University (Science and Technology), 2007, 38(5): 981−986.

[5] XIANG Jun, ZENG Qingyuan, LOU Ping. Transverse vibration of train-bridge and train-track time varying system and the theory of random energy analysis for train derailment[J]. Vehicle System Dynamics, 2004, 41(2): 129−155.

[6] 毕继红, 姜嘉琳, 关健. 混凝土护栏在超高速磁悬浮列车碰撞下的有限元分析[J]. 铁道科学与工程学报, 2018, 15(9): 2196−2201. BI Jihong, JIANG Jialin, GUAN Jian. Finite element modeling of concrete guardrail's responses under impact of ultrahigh speed maglev train[J]. Journal of Railway Science and Engineering, 2018, 15(9): 2196−2201.

[7] Kim K J, Han J B, Han H S, et al. Coupled vibration analysis of Maglev vehicle-guideway while standing still or moving at low speeds[J]. Vehicle System Dynamics, 2015, 53(4): 587−601.

[8] WANG J, JIN X, CAO Y. High-speed maglev train guideway-tunnel-soil modeling of ground vibration[C]// Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2011.

[9] 高祥. 基于ANYSY/LS-DYNA的铁道车辆单车碰撞问题建模与仿真研究[D]. 北京: 北京交通大学, 2008. GAO Xiang. Study on modeling and simulation of crash problems of single railway vehicle based on ANSYS/LS- DYNA[D]. Beijing: Beijing Jiaotong University, 2008.

[10] ZHOU Hechao, ZHANG Jimin, Hecht M. Three- dimensional derailment analysis of crashed freight trains[J]. Vehicle System Dynamics, 2014, 52(3): 341− 361.

[11] XIE Suchao, ZHOU Hui. Research on the crashworthy structures of subway vehicles[J]. International Journal of Crashworthiness, 2014, 19(6): 555−566.

[12] Baykasoğlu C, Sünbüloğlu E, Bozdağ S E, et al. Railroad passenger car collision analysis and modifications for improved crashworthiness[J]. International Journal of Crashworthiness, 2011, 16(3): 319−329.

[13] 王川. 客货共线铁路桥梁列车脱轨后与防护墙碰撞过程研究[D]. 长沙: 中南大学, 2014. WANG Chuan. Research on the process of collision between derailed trains and protective walls on mixed passenger and freight railway bridges[D]. Changsha: Central South University, 2014.

[14] 肖乾, 王成国, 周新建, 等. 不同摩擦系数条件下的轮轨滚动接触特性分析[J]. 中国铁道科学, 2011, 32(4): 66−71. XIAO Qian, WANG Chengguo, ZHOU Xinjian, et al. Analysis on the characteristics of wheel/rail rolling contact under different friction coefficient[J]. China Railway Science, 2011, 32(4): 66−71.

[15] 肖乾, 林凤涛, 王成国, 等. 变摩擦系数条件下的轮轨滚动接触特性分析[J]. 铁道学报, 2012, 34(6): 24−28. XIAO Qian, LIN Fengtao, WANG Chengguo, et al. Analysis on wheel-rail rolling contact characteristics with variable friction coefficient[J]. Journal of the China Railway Society, 2012, 34(6): 24−28.

Study on train-bridge protecting wall collision based on finite element simulation

LÜ Siyu1, 2, 3, ZHONG Mu1, 2, 3, LU Zhaijun1, 2, 3, LIU Xiang1, 2, 3

(1. Key Laboratory of Traffic Safety on Track, Central South University, Ministry of Education, Changsha 410075, China;2. Joint International Research Laboratory of Key Technology for Rail Traffic Safety, Changsha 410075, China;3. National & Local Joint Engineering Research Center of Safety Technology for Rail Vehicle, Changsha 410075, China)

The research on protection capability of bridge protecting wall structure is scarce, and the actual vehicle experiment is almost zero. Based on the finite element theory, the model of the collision between the train and the protecting wall on the unballasted track was established by Hypermesh. The process of collision was analyzed and studied by numerical simulation method. After analysis and research, the force and deformation of the protecting wall and the motion character of the train under different speeds and different angles of impact were obtained. The results show that when the train collides with the protecting wall at a lower speed and a smaller angle of attack, the protecting wall is less damaged. When the collision speed is higher and the angle of attack is larger, the protecting wall is more damaged, and the train has a slight climbing phenomenon. But it can still play a role of limiting guidance for derailed trains. After the protecting wall is raised, the collision model under the relevant working conditions is established for simulation calculation. It is found that the increased protecting wallcan effectively inhibit the train from climbing the wall by analyzing the collision process, the impact force, the deflection angle and the speed. The train has better running stability.

train; protecting wall; finite element simulation; collision process

10.19713/j.cnki.43−1423/u. T20190725

T270.2

A

1672 − 7029(2020)01 − 0008 − 08

2019−08−17

鲁寨军(1975−)，男，湖南醴陵人，教授，博士，从事轨道车辆结构和动力学研究；E−mail：qlzjzd@csu.ed.cn

(编辑 阳丽霞)