高职“4.5+0.5”人才培养模式下数学课程改革研究

周丽霞

（无锡城市职业技术学院 会计系，江苏 无锡 214000）

一、高职“4.5+0.5”人才培养模式解读

所谓“4.5+0.5”人才培养模式［1］，指的是江苏省关于初中起点的五年制高等职业教育所实行的“4.5+0.5”人才培养模式。五年人才培养计划分为两个阶段，在校学习时间为九个学期即4.5 年，校外顶岗实习时间为一学期即0.5 年，该人才培养计划是依据教育部及江苏省教育厅的相关文件，将五年制高职专业的人才培养模式由“4+1”模式转变而来。

这次人才培养计划调整，最大的变化在于突出了对文化课的重视。“4+1”模式强调的是专业技能的学习，语文、数学等公共基础课程的课时较少，文化课教学内容的深度和广度不够。想继续学历深造的学生，必须参加有关高校的入学考试，其中语文、数学、英语是必考科目，由于“4+1”人才培养计划的文化课课时较少，教学内容较少，这对有深造学习需求的学生形成了很大的障碍。调整后的“4.5+0.5”人才培养方案，增加了公共基础课课时，尤其是数学课程从之前的两年四个学期增加到四年八个学期，内容从初等数学到高等数学，更加注重学生的继续教育问题，注重学生的终身学习以及与专业知识的结合，提升专业学习能力。同时新的人才培养方案中首次提出了职业教育的学业水平测试，在高职三年级上学期由江苏省联合职业技术学院牵头进行全省性的学业水平测试，包括公共基础、专业基础、专业技能三部分。该项测试对各职业院校的公共基础课程教学提出了较高的要求，随着学业水平测试从普通教育延伸到职业教育，文化课的重要性必然会在职业学校教学中得以体现，直接促进了传统数学教学模式和教学方法的改革。

二、数学课程教学内容的改革

在原有“4+1”人才培养模式下，数学课程开设为两年四学期，内容只涉及初等数学部分，包括集合与不等式、函数、三角函数、复数、立体几何、解析几何、排列组合、概率统计等内容，这些内容是高职学生的短板，一是对很多专业课所需要的数学基础知识学得太肤浅，很多专业课需要使用高等数学知识来解决相关专业问题，而学生在两年的数学学习中根本未学习高等数学知识，为学生的后续学习造成了困扰，专业课教师也烦恼；二是对很多有升学愿望的学生来说，要经过成人高考、专接本等考试才能升入本科院校进一步深造，而这些考试不可避免地要考核数学，如果不能很好地掌握高等数学考核的内容，升学考试很难取得理想的成绩，很多学生因此导致不能进一步深造。

新的“4.5+0.5”人才培养方案很好地解决了数学课程存在的两个问题。根据新的人才培养方案，数学课程授课计划由两年延伸为四年，总课时增加了近一倍，教学内容也从初等数学延伸到高等数学，包括导数与微积分、空间解析几何、微分方程、线性代数、多元函数微分及多重积分等内容。增加课时可以拓展学生掌握知识的深度和广度，同时增加高等数学内容，可以让学生储备足够的学习专业课所需的数学基础知识，从而让学生在后续学习专业理论课时更加得心应手，对专业知识的掌握和理解更快，比如机械专业的学生在学习专业课程中的圆轴扭转时，横截面上的应力和强度条件需要用到微分的概念，利用微分进行近似计算；再如电气自动化专业学生在学习电机原理与电力拖动课程时，变压器、三相异步电动机的原理分析需要用到函数与极限、导数等数学知识，如果没有高等数学知识的学习，专业课的学习将无从下手。

三、数学课程教学模式的改革

人才培养模式的改变直接影响高职院校的数学课程体系，教学模式必然要进行相应的改革，以弥补“4+1”人才培养方案的短板，如何找到一个更优化的教学模式，最大限度地发挥新的人才培养方案的优势，需要进行专门的课题研究，探索出一套行之有效的教学模式和教学方法。高职的教学模式基本还是参照高中的教学模式，以应对职业学校学业水平测试，高等数学课程侧重于研究如何和专业课对接、如何更好地服务于专业，如何让学生学会学习，以达到终身学习的目的。下面以线性代数［3］的学习为例，探讨教学模式和教学方法的改革与实践。

根据人才培养方案要求，线性代数章节作为电气自动化专业必修内容进行教学，这一内容的学习在原有人才培养方案中并未涉及，也没有现成的教学模式可供参考，学校教研室在充分研讨后决定，采用以信息化教学为主导的教学模式，联合学校的超星慕课平台以及机房等设备，将课堂放入机房，使数学课程与信息化手段完美融合，比如关于行列式的计算，我们传统的计算是定义法，即按行（列）展开并利用性质计算，这种方法在低阶行列式的计算中很容易求解，但对于高阶行列式，人工计算不但耗时，而且容易出错。我们以Matlab解决这一典型问题为例，来求方阵行列式的值。

我们先用传统的计算方法，利用行列式的性质计算如下：

其中，D1是一个范德蒙德［4］行列式，则根据范德蒙德行列式计算公式可得

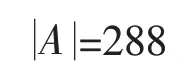
接下来我们应用数学教学软件进行解题。

对于给定的方阵A，在Matlab 中求解行列式的公式为：det（A），该公式可以直接显示行列式的计算结果，演示如下：

在软件中输入行列式：

显而易见，数学软件在这一知识点的应用上得心应手，大大简化了计算量，并且一目了然，程序简单，适合初学者进行研究性学习。

从实践效果来看，每节课都能利用多媒体课堂、机房教学，在讲解线性代数相关理论原理的基础上熟知数学软件的使用，使线性代数的教学和信息化软件的应用有机结合，同时又不至于弱化理论教学，提升学生对线性代数的学习兴趣，激发学生学习线性代数的积极性。

四、结合人才培养计划开展课题研究

由于新的人才培养方案增加了数学教学课时，坚持以实用性为目的，把教学的侧重点定位在对学生数学应用能力和终身学习能力的培养上，培养学生的数学素养，使学生终身受益，对学生的后续发展起到以点带面的重要作用。这就需要借助现代信息技术手段，引入新的教学模式和教学方法。

数学教研室针对机电类专业的学生进行五年制高职数学建模与Matlab相融合的教学实验研究，在机电工程系和自动化工程系五年制高职的1511、1512、1513、1514四个班级进行试点，通过课题研究和实践，师生普遍认为原本枯燥乏味的高等数学如果和生活实际联系起来，特别是学生身边的实际问题联系起来，就变得有了价值，学习也有了驱动力。同时，基于信息化课程开发的数学实验课让学生体验到崭新的数学学习模式，基于开放式的网络教学平台，其灵活的学习方式都可以成为学生自主学习的催化剂，学生学习数学的积极性以及学习能力的提升效果都相当明显。

在课题研究中，把数学建模和数学软件相结合并应用于数学教学实验，对数学教师提出了更高的要求。首先，教师必须不断更新自身的知识，以适应时代发展的需要和数学学习的需要；其次，教师要对数学建模的方式和相关软件的应用进行学习，这样才能对高职生的数学学习进行指导；最后，为了更好地实现教学目标，完成教学任务，教师在具体的教学实验之前，还要学习录制相应的微课或慕课，帮助学生做好课前的预习或课后的学习补充整理，这些都需要教师利用课余时间自主学习。随着课题研究的深入开展，我们课题组的许多教师由传统的经验型向科研型、学者型转变，教师的业务素质、教育素养和教学能力等都有了较大的提高。

在教学实验中引入数学软件，给学生的数学解题带来了便利，也起到了一个很好的引导和示范作用，有个别对计算机比较感兴趣的学生就此抓住机会，利用课余时间自学数学软件。学生在使用数学软件的过程中，势必先要掌握数学知识，遇到问题会主动与任课教师讨论，学习的主观能动性被挖掘出来了。

利用现代教学技术辅助线性代数教学，既能激发学生学习兴趣，解放学生学习压力，提升课程内涵，又能兼顾线性代数学科体系特征，凸显应用功能的重要途径。将数学软件作为一个重要工具引入线性代数的研究，已成为高职数学教学改革的热点。