融合初值校准与二阶逼近的单星测频定位算法*

张金艺，王 彬，秦 奋,，朱浤涛

(1. 上海大学 通信与信息工程学院， 上海 200444； 2. 上海大学 微电子研究与开发中心， 上海 200072；3. 上海航天电子技术研究所， 上海 201109)

深空探测对人类研究宇宙、开发太空资源具有重大的意义。进入21世纪以来，各国对于外太空的探索愈发白热化。探测器定位是深空探测中一个重要的组成部分，在地外星体探测中，围绕特定星体构建全球定位系统的成本难以估量。单星定位系统借助其成本低、体积小、结构简单的优势，可以迅速发射部署，为目标实现定位服务[1]。单星定位可以分为单星测向定位和单星测频定位。单星测向定位通过干涉仪求解相位模糊得到定位目标到卫星的方向角和俯仰角，并结合地球模型实现单脉冲瞬时定位[2]。然而干涉仪天线结构复杂，使得方向角和俯仰角求解困难，其定位误差达几十千米[3]。单星测频定位利用多普勒效应，由卫星与定位目标相对运动造成的多普勒频移来反演地面定位目标的位置[4]，其误差为几千米，因而单星测频定位相对于单星测向定位适用性更高。然而单星测频定位具有定位固有信息不足的缺陷，使得定位精度难以达到实用的要求，近年来，借助外部辅助信息来提升定位精度是一种常用的手段。

为提高单星测频定位的精度，陆安南等提出一种测频测相位差组合定位算法[5]，定位精度相对单一方法较高，达到千米级，但是该方法需多次测量信号的频率，仅适用于长时间通信信号的定位。Zhu等提出了消除二阶导数的影响从而提高多普勒频率测量精度的算法[6]，但是没有在方程求解层面解决定位误差问题。徐义、Liang等提出一种利用网格搜索法求解最优值的单星测频定位算法[7-8]，网格搜索法简单易行，但是实际运用中计算量大而且精度受限。Yang、狄慧等提出一种基于径向加速度的单星定位算法[9-10]，利用运动学原理通过到达脉冲提取径向加速度，之后采用粒子群优化(Particle Swarm Optimization, PSO)算法求解定位目标位置，在一定程度上减小了定位误差，但该算法对径向加速度估计精度要求很高，且计算复杂度较高。Zhao等提出一种基于神经网络的波束扫描单星定位算法[11]，通过获取波束的坐标信息近似预测目标位置，利用反向传播(Back Propagation, BP)神经网络学习波束信息以得到定位结果，但是波束扫描对卫星发射机功率要求过高，因此该算法实际应用效果不佳。

对于单星测频定位而言，传统的求解算法由于初值选取问题导致误差过大，而将优化方案引入定位求解又会增加额外的计算开销。为了解决这个问题，本文提出了融合初值校准与二阶逼近的单星测频定位算法，利用初值校准降低算法迭代次数，通过二阶逼近提高定位精度。

1 多普勒单星定位问题剖析

1.1 基于多普勒效应的单星测频定位算法

单星测频定位基于多普勒效应，当卫星经过地面静止定位目标的上空时，由于卫星与定位目标具有相对运动，卫星接收信号频率与定位目标发射信号频率存在偏差。通过数字信号处理从接收信号中得到多普勒变化率，进而反演出目标源的位置。单星测频定位只需要一颗卫星多次测量即可实现，具有结构简单、功耗低的优点。

(1)

将卫星速度、位置以及待求定位目标位置代入式(1)可得定位方程：

(2)

式(2)中，卫星的位置和速度信息已知，发射频率和接收频率可测，待求量只有定位目标的位置(x，y，z)。理论上，对于3个未知量，联立3个不同时刻的定位方程可求解出定位结果。为求解联立的非线性方程组，可以通过将方程线性化、选取合适的初值迭代来实现。多普勒单星定位算法在整体求解过程中，存在初值选取和定位方程求解2个问题。

图1 单星测频定位原理图Fig.1 Schematic of single-satellite localization from frequency measurements

1.2 初值选取问题剖析

(3)

但是式(3)所示的非线性方程组求解困难，为了快速得到初值，多普勒单星定位算法选取t0时刻卫星星下点作为迭代求解的初值。假设t0时刻卫星的位置为(X0，Y0，Z0)，卫星的轨道高度为h，则初值的坐标可以表示为：

(4)

然而在实际应用中，定位目标并不一定与卫星轨道在同一平面内(如图2所示)。当定位目标与卫星轨道平面垂直距离增大时，星下点距真实位置的误差变大，以星下点为初值会造成算法复杂度增加甚至迭代算法不收敛。

图2 星下点与定位目标不匹配示意Fig.2 Mismatch between sub-satellite point and localization target

1.3 定位方程求解问题剖析

定位方程求解决定了定位精度，在多普勒单星定位算法中，非线性方程组难以直接求解，一般通过泰勒展开将定位方程组线性化，把星下点(x0，y0，z0)作为迭代初值，迭代求解线性化的定位方程。

为便于分析，由式(2)，将定位方程写为如下形式：

fi=gi(x,y,z)

(5)

将其在(x0，y0，z0)点泰勒展开并略去高阶项可以得到：

gi(x0,y0,z0)+gi(x0,y0,z0)

(6)

进一步简化可以得到：

(7)

式中，Δfi=fi-gi(x0,y0,z0)为ti时刻的多普勒频移，Δx=x-x0、Δy=y-y0和Δz=z-z0分别表示迭代前后3个坐标轴的估计差值。联立3个时刻的线性化定位方程组求解估计差值，或者联立3个以上的方程组通过最小二乘法获取估计差值最优解，并设定阈值或迭代次数得到最终定位结果。

将定位方程泰勒展开的本质是用多项式去逼近原有的定位方程。然而在其线性化的过程中，复杂的高阶项被舍去，仅含一阶级数的泰勒展开式往往无法较好地拟合原有定位方程，一些复杂的定位信息在舍去高阶项的过程中被略去，造成单星定位的误差始终无法减小。在多普勒单星定位算法中，算法的缺陷使提高频率测量精度等手段对定位精度的提高有限，本文将对定位方程的求解提出新的思路。

2 高精度快速单星测频定位算法

多普勒单星定位算法中的初值选取问题和定位方程求解问题极大地影响了定位求解的速度和精度。通过观察单星测频定位方程式(2)可以发现，定位方程右边是由常函数、指数函数、幂函数等基本函数经过数次有理运算得到的初等函数，其在零点附近区域连续。同时，在物理世界中卫星收到了目标源发射的信号，因此定位方程必有解。在这两个条件下，由收敛性可知当初始值位于零点附近区域时，迭代法的结果必定收敛。本文提出的融合初值校准与二阶逼近的单星测频定位算法通过初值校准使得初始值更加逼近定位目标的真实位置(即定位方程的根)，进而减少迭代次数；通过定位方程泰勒展开式保留二阶定位信息，更好地拟合原有方程，提高定位精度，从而实现高精度快速单星测频定位算法。

2.1 初值校准

图3 初值校准模型Fig.3 Initial value calibration model

由t0时刻定位目标和卫星的几何关系可以得到，卫星的速度矢量V0与由地心O、位置P0以及定位目标位置S构成的平面垂直，因此可以很容易地得出下列3个方程。其中式(8)表示该时刻卫星运动方向和定位目标与地心的连线垂直，式(9)为△OSP0的余弦定理，式(10)表示定位目标处于球体表面。

(8)

(9)

x2+y2+z2=r2

(10)

式(8)和式(9)为三元一次方程，联立式(8)和式(9)可以得到x0和y0关于z0的表达式，将其代入式(10)可以得到一个关于z0的一元二次方程。本文所提出的初值计算方法解决了多普勒单星定位算法初值选取困难的问题，相比优化法引入大量计算代价的做法降低了定位解算时间、提高了定位效率。在实际应用中，直接获得多普勒频移为零时的测距信息可能存在一定的困难，可以在多普勒频移由正到零到负的时间段(即卫星靠近定位目标、卫星与定位目标相对距离最近、卫星开始远离定位目标)不间断地测距，选取多普勒频移绝对值最小时刻的位置、速度以及测距信息代入上面方程组，求解出校准的初值。

在初值校准模型中，求解初值方程组时会得到两个实数解。其中S点为定位目标真实点，S′为定位目标关于卫星轨道平面的镜像点。一般可以通过两种方法去除镜像点：①定位过程中目标点总是位于轨道平面的一侧。利用这个特点，将卫星接收天线的主瓣朝向目标点一侧，将副瓣朝向镜像点一侧，在定位期间判断接收信号的来波方向确定目标点位置。②在不增加新的硬件和设备信息的前提下，可以通过卫星的轨道特性来解决。通常单星测频定位的卫星为低轨道卫星，随着地球的自转，卫星轨道平面在地球坐标系下的位置将发生变化，将两次单星测频定位结果作对比，其交集即为目标点。

2.2 含二阶定位信息的方程求解

牛顿迭代法求解定位方程组的本质是通过泰勒展开，用一个有限的多项式去逼近原有的方程，使得方程的求解简单化。在多普勒单星定位算法中，泰勒展开的高阶项被舍去，定位方程简化为一个线性方程，算法复杂度大大降低。然而，高阶项的舍去也造成了一定的后果，即多项式方程组与原定位方程拟合度不够。在一些其他的非线性方程组求解中，高阶项的舍去不会造成比较大的偏差，然而在多普勒单星定位方程中，待求的坐标点S(x，y，z)可以由cosθi演绎获得，那么定位方程的展开实质是对cosθi的泰勒展开。当θi的误差在1°左右时，cosθi的误差在可忽略的数量级，但星球体的巨大半径(例如在地球上，经度每相差1°，实际距离相差在111 km左右)会使得最终的定位结果产生数千米甚至数十千米级的误差。如果单星测频定位方程组的泰勒展开项不足以逼近原有的方程，那么在求解过程中就人为地引入了千米级的误差，这也是单星测频定位误差难以减小的原因。为了解决这个缺陷，将泰勒展开的二阶级数平方项保留，并提出了求解算法。

将式(2)泰勒展开，保留二阶级数平方项：

(11)

式(11)中含有平方项，难以直接求解。在本文提出的算法中，初值校准使得初始点位置接近目标的真实位置，因此每次迭代后，x、y、z三个方向上的差量较小，平方项和一次项对于最终定位结果的影响在同一级别。为了简化迭代过程，令Δu=Δx2，Δv=Δy2，Δw=Δz2，将式(11)化为线性方程：

(12)

其中，Δfi为ti时刻多普勒频移，Δx、Δy和Δz分别表示前后两次3个坐标轴的估计差值，Δu、Δv、Δw分别表示前后两次3个坐标轴的估计差值的平方。选取6个或以上时刻的观测数据代入式(12)，可以得到定位方程组：

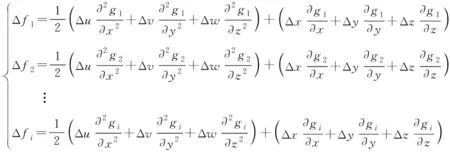
(13)

在线性方程组(13)中，令

(14)

(15)

(16)

将方程组改为矩阵形式：

F=GS

(17)

对于式(17)，当观测数据超过6个时用最小二乘法求解：

S=(GTG)-1GTF

(18)

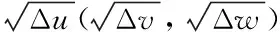
3 仿真与结果分析

3.1 STK仿真平台搭建

本文利用卫星工具包(Satellite Tool Kit, STK)软件来搭建仿真平台。为了验证所提算法的适用性，选取仿真环境为火星，设置卫星轨道为圆轨道，高度为800 km，轨道倾角为45°，载频为4.5 GHz，信号采样时间为1 s。在卫星通信的最大范围内随机选取10个定位点，利用STK的access报告获取卫星星历信息、速度位置信息以及多普勒频移信息，作为算法的输入参数。

3.2 实验结果分析

在3.1小节搭建的仿真平台中，分别设置外部测距的误差为1 km和0 km，设置卫星接收机采样频率为1 Hz，利用STK获取多普勒频移为0时的卫星位置及运动状态数据。在仿真过程中，由式(1)可以得到定位期间接收频率随时间减小的特性，在选取观测量时只需判断其是否在前一秒和后一秒观测量值组成的区间内来避免观测异常值对结果的影响。为了保证仿真结果的严谨性，选取多普勒频移为0前180 s、120 s、60 s以及多普勒频移为0后60 s、120 s、180 s共6组接收频率数据，对多普勒单星定位算法[12]和本文算法各自建立6个方程联立的定位方程组，从初值误差、迭代收敛次数和定位误差方面与多普勒单星定位算法进行对比，从定位误差方面与基于神经网络的单星波束扫描定位算法[13]进行对比。

3.2.1 初值误差分析

在3.1小节的仿真平台中，将获得的卫星位置及运动状态数据代入2.1小节中的初值方程组进行求解，并与多普勒单星定位算法的星下点初值进行对比，结果如图4所示。

图4 初值误差对比Fig.4 Comparison of initial value error

从图4可以看出，多普勒单星定位算法的初值平均误差在18.77 km左右，而本文提出算法的初值平均误差在测距误差为1 km的情况下为6.23 km，减小了66.8%左右。从图中还可以看到，测距误差为0 km时，初值平均误差与测距误差在1 km情况下的非常接近，这是因为在离地800 km的高度，初值校准的结果对1 km级别的测距误差并不敏感，这也印证了2.1小节中阐述的“初值校准对测距误差要求很低”的说法。精确的初值不仅可以减少后续迭代算法的次数，同时还可避免迭代不收敛情况的发生。

3.2.2 迭代收敛次数与定位误差分析

为了验证“初值校准”和“二阶逼近”对于定位效果的影响，在前文的10个初值基础上设置4组实验进行对照实验。第一组为多普勒单星定位算法；第二组为测距误差1 km下的二阶逼近算法；第三组为测距误差0 km下的二阶逼近算法；第四组为多普勒单星定位算法初值代入二阶逼近迭代算法。记录以上4组实验的迭代收敛次数和定位误差，结果如表1和表2所示。同时，将所提出的算法与基于神经网络的单星波束扫描定位算法在定位误差方面进行对比，结果如图5所示。

表1 迭代收敛次数对比

表2 定位误差对比

联合表1和表2进行综合比对：比较第一组和第三组可以得到，多普勒单星定位算法的迭代收敛次数在6～8，平均误差在2.247 km左右，而本文提出的算法迭代收敛次数为3～5，平均误差在0.935 km左右，本文算法在迭代收敛次数和定位误差上均有较大提升；比较第二组和第三组可以得到，本文算法在外部测距误差为1 km和 0 km 情况下的迭代收敛次数和定位误差一致，说明最终的定位误差不受测距误差的影响；比较第三组和第四组可以得到，第四组的迭代收敛次数高于第三组，第三、第四两组的定位误差一致，说明初值校准降低了算法迭代次数，并且避免了定位结果不收敛情况的产生；比较第一组和第四组可以得到，两者的迭代收敛次数基本相同，第四组的定位误差低于第一组，说明二阶逼近实现了定位误差的降低，提高了定位精度。

图5 定位误差对比Fig.5 Comparison of localization error

由图5可以得到，本文提出的算法的平均误差为0.935 km，与基于神经网络的单星波束扫描定位算法平均0.880 km的误差十分接近。仿真表明，本文提出的算法在迭代次数和定位误差方面相比多普勒单星定位算法分别降低了49.5%和58.4%左右，同时杜绝了定位结果不收敛的情形，对于传统算法而言是一次较大的突破。其定位误差与基于神经网络的算法十分接近，并且由于计算量低，具有更好的适用性。

4 结论

针对单星测频定位误差较大的问题，提出了一种融合初值校准与二阶逼近的单星测频定位算法，利用测距得到多普勒频移为零时卫星与定位目标的距离信息，代入轨道平面与定位目标的几何关系解算出校准的定位初值，将校准初值代入含二阶定位信息的定位方程泰勒展开式，联立6个时刻的定位方程组迭代求解出最终结果。本文提出的算法无论在迭代次数还是定位精度上，相比多普勒单星定位算法都有很大的提高。同时，算法改进使得定位方程组数量增加，在实际应用中选取多普勒频移零时刻前后各3个时间点列出定位方程，能够有效地利用测量数据，降低频率测量的随机误差对定位结果的影响。