基于傅里叶级数分析的各向异性参数估计及裂缝预测

宋维琪,徐月森,张云银,张营革,高秋菊,魏欣伟,张明秀

(1.中国石油大学(华东)地球科学与技术学院,山东青岛266555;2.中国石油化工股份有限公司胜利油田分公司物探研究院,山东东营257055)

随着各向异性介质理论研究的发展与完善,非常规致密油气储层作为当前油气勘探的重点领域之一,相关的地震预测技术也在不断深入发展,并逐渐应用到生产实际领域[1-2]。实际地球物理介质都不同程度地存在着各向异性的特性。作为非常规致密油气藏,裂缝储层是典型的各向异性介质[3-4]。地下地层中发育的近垂直裂缝,不仅是良好的油气运输通道,也是良好的油气存储空间,因此研究裂缝储层具有重要的实用价值[5]。

各向异性介质理论在19世纪末被引入地球物理勘探领域,并在近二、三十年得到了长足的发展与应用。CRAMPIN[6-7]提出方位各向异性和横波分裂等概念,极大地推动了各向异性理论在应用领域的发展;THOMSEN[8],HUDSON[9]先后提出不同的各向异性理论模型,对该理论的实际应用做出了重要贡献;RUGER[10]提出具有水平对称轴的横向各向同性介质(HTI)纵波反射系数近似方程,推动了利用纵波方位各向异性信息预测裂缝技术的发展;王顺昌等[11]研究了倾斜裂缝地层qP波方位反射系数椭圆特征,将qP波方位反射系数拟合成椭圆,得到了椭圆参数与裂缝密度、裂缝倾向和裂缝倾角的关系;杨敏等[12]研究了裂缝参数对地震方位各向异性特征的影响,发现HTI介质、裂缝介质的各向异性特征随裂缝密度增加而增强,P波速度、反射系数随方位角呈现椭圆、周期性变化,各向异性椭圆方位指示裂缝发育方向;王洪求等[13]分析了不同地震属性的方位各向异性并展开裂缝预测;杨勤勇等[14]研究了纵波方位各向异性及其在裂缝检测中的应用,证实了垂直裂缝存在方位各向异性特征,提出了基于二维多方位预测的精确解法和基于三维多方位预测的最小二乘法;王康宁等[15]研究了基于HTI模型的纵波方位各向异性反射系数近似公式的傅里叶级数展开式;多位学者研究了具有两组正交对称轴的各向同性的纵波反射系数近似公式的傅里叶级数展开[16-20]。本文将纵波反射系数近似公式展开成傅里叶级数形式,并针对不同方位角范围的数据,利用二倍角公式进一步展开,避免了在最小二乘拟合条件下提取傅里叶级数系数,造成同一个cosnφ项对应两个各向异性反射系数而导致的拟合结果非唯一,将该傅里叶级数系数拟合方法应用于HTI模型和实际地震资料,可实现各向异性参数估计和裂缝预测。

1 基于傅里叶级数分析的各向异性参数预测

1.1 基于HTI模型的纵波反射系数公式傅里叶级数展开式

随地震观测方位发生变化的纵波反射系数序列可以表示为周期为2π的函数,傅里叶级数展开形式为[15]:

(1)

式中:φ为方位角;a0,an,bn(n=1,2)为常数。假设裂缝介质为HTI介质,结合SCHOENBERG等[21]裂缝介质理论模型,得到傅里叶级数形式的纵波方位各向异性反射系数RPP(i,φ)的近似公式[15]为:

RPP(i,φ)=a0+a2cos2φ+a4cos4φ

(2)

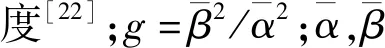
传统的地震属性方位各向异性椭圆拟合方法通常基于Ruger两项近似方程,当选定某一个固定的入射角时,将纵波反射系数公式进行傅里叶级数展开,提取二阶项系数a2,可直接得到裂缝发育密度。

1.2 基于二倍角的纵波反射系数公式傅里叶级数展开式

利用纵波反射系数公式的傅里叶级数展开式预测裂缝发育密度和走向,通常采用反演方法或拟合方法。考虑到实际地震资料信噪比低的特点,本文采用拟合方法估计各向异性参数。

当地震数据方位角的范围为0～45°时,针对(2)式,可采用最小二乘拟合方法计算傅里叶级数系数a2;但对于方位角范围在0～90°的地震数据,采用(2)式拟合a2并不合适,因为此时一个cos4φ项在拟合时会对应两个RPP值,导致拟合结果非唯一。因此需要利用二倍角公式将(2)式展开成如下形式再进行拟合:

RPP(i,φ)=a0+a2cos2φ+a4cos4φ

=2a4cos22φ+a2cos2φ+(a0-a4)

(3)

针对实际应用中方位角范围为0～180°的地震数据,需要将(3)式继续用二倍角公式展开,否则在拟合时,一个cos2φ项也会对应两个振幅值,导致拟合结果不确定。如图1所示,拟合傅里叶级数系数a2时,一个cos2φ项本应对应一个振幅值,但因为数据方位角范围扩大至0～180°,使得一个cos(2φ)项对应两个振幅值,导致拟合结果存在非唯一性。图中蓝色曲线代表0～180°方位角范围的实际地震数据,小圆圈代表9个不同方位的振幅值,紫色曲线代表拟合数据。

根据二倍角公式将(3)式展开为:

RPP(i,φ)=8a4cos4φ+(2a2-8a4)cos2φ+
(a0-a2+a4)

(4)

对于方位角范围在0～180°的数据,一个cosφ项对应一个RPP值,拟合结果的唯一性得到保障。

图1 未用二倍角公式展开时错误的拟合结果

2 HTI介质理论模型试算

HTI介质是具有水平对称轴的横向各向同性介质,弹性系数矩阵由5个独立的弹性常数表示。本文采用的双层HTI介质理论模型各向异性参数如表1所示。

各向同性面平行于纵轴,i为入射角。越靠近各向异性对称轴,介质的各向异性就会越强。利用最小二乘拟合的方法,根据双层HTI介质理论模型拟合a2,结果如图2a所示,小圆圈代表不同入射角时的a2值,紫色曲线为拟合曲线,可以看出随着入射角的增加,a2的绝对值不断增大,拟合得到的a2变化趋势与各向异性参数理论公式计算结果(图2b)一致,说明本文方法能有效地反映介质的各向异性特征。

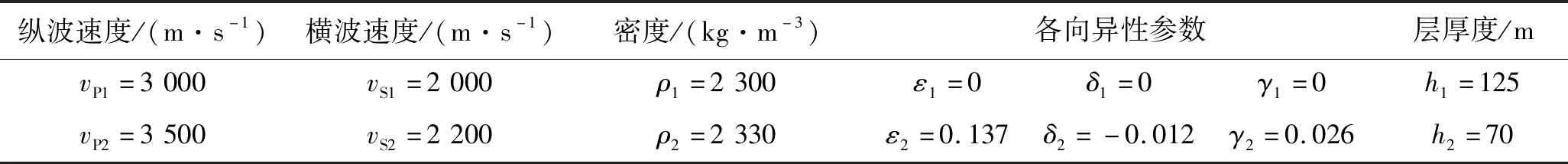
表1 双层HTI介质理论模型各向异性参数

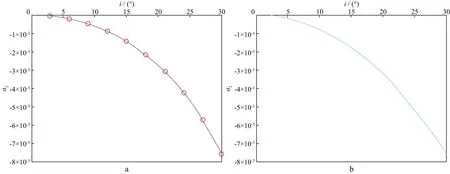
图2 傅里叶级数系数a2随入射角变化情况a 本文方法拟合; b 理论公式计算

3 实际应用

将本文方法应用于渤南地区四扣工区致密砂岩的储层研究。研究区内地质构造复杂,断层、裂缝等发育;致密砂岩储层基质颗粒杂乱,分选性差,渗透率低,非均质性强,岩性变化大;地层的形成和演化过程非常复杂,各向异性特征明显。利用基于两项Ruger方程的地震属性方位各向异性椭圆拟合方法即传统方法,对比验证本文方法的有效性和精度。

渤南地区地震资料包含9个方位角(0～180°)数据,在远、中、近3个固定偏移距上各自形成了9个分方位角道集叠加的地震数据,每隔20°划分一个方位角道集,提取每个方位角的平均振幅属性,将每一个点的振幅属性值A按照其方位角分解为:

(5)

式中:φ为该方位角道集的中心方位角;Ax,Ay分别为沿横轴、纵轴方向的振幅属性值。

因近偏移距地震数据各向异性不明显,远偏移距地震数据的信噪比低而且数据不完整,故本文使用中偏移距的地震数据进行计算。首先将某一个坐标点9个方位的每一个地震振幅属性值都分别分解为Ax和Ay,然后进行振幅属性方位各向异性椭圆拟合,最后得到的椭圆拟合长短轴之比的结果如图3所示。采用地震属性方位各向异性椭圆拟合方法预测裂缝发育密度和走向时,对属性值波动大、信噪比低的数据,得到的计算结果精度低,抗噪能力差。

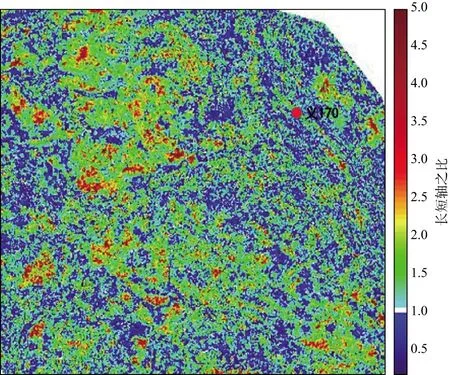
图3 中偏移距地震数据椭圆拟合长短轴之比的结果

由图4可知该地区发育北西—南东向的断层,由图5可知,本文方法拟合结果与实际一致,说明本文方法在预测裂缝发育密度和走向时计算精度高,抗噪能力强,效果优于传统的椭圆拟合方法。采用本文方法对该地区地震资料进行计算,拟合傅里叶级数第2项系数a2,对比未利用二倍角公式展开和利用二倍角公式展开后的傅里叶级数系数a2拟合结果(图5)发现,后者的拟合精确明显提高,更为准确地实现了各向异性参数估计和裂缝预测。

图4 义170井裂缝玫瑰图

图5 利用中偏移距地震资料拟合的傅里叶级数系数a2a 未用二倍角公式展开; b利用二倍角公式展开后

4 结论

将HTI理论模型纵波反射系数公式的傅里叶级数展开式,利用二倍角公式进一步展开,避免了同一个cosnφ项对应两个RPP值导致的拟合结果非唯一性问题,提高了基于拟合的各向异性参数估计和裂缝预测的准确性。本文方法在HTI模型和实际地震资料应用结果表明,相较于传统的椭圆拟合方法,本文方法抗噪能力更强,计算精度更高,更为准确地实现了渤南地区各向异性参数估计和裂缝发育的预测。