面向近地表品质调查的微测井采集及应用效果分析
2020-02-07刘宜文杨晓海王晓涛
蒋 立,刘宜文,范 旭,杨晓海,王晓涛
(中国石油天然气股份有限公司新疆油田分公司勘探开发研究院地球物理研究所,新疆乌鲁木齐830013)
在进行近地表Q补偿时,无论是采用补偿系数法[1],还是采用粘弹波动方程延拓方法[2],都必须准确计算出近地表品质因子Q。利用地震数据的频率和振幅计算出的Q值被称为相对Q值[3-4],其准确性较差,利用相对Q值进行近地表Q补偿会造成地震数据高频端稳定性变差,信噪比降低。为了提高近地表Q场的精度,李国发等[5]采用双井微测井实测近地表Q值;王静等[6]利用全井段VSP资料计算近地表Q值,利用实测Q值约束相对Q场,建立准确的近地表Q场。于承业等[7]利用双井微测井资料,通过求解地面和井下检波器的峰值频率变化方程组,获得了近地表Q值的解析解,但该方法没有考虑炮检点耦合对Q值计算结果的影响。丁冠东等[8]发现激发深度和检波器耦合效应会影响微测井信号的频谱特征,利用共激发点资料消除激发条件差异,但其对于检波点耦合差异,只是通过提高工艺水平来消除。翟桐立等[9]提出深井激发、浅井和地面短排列接收的近地表Q值估算方法,该方法可避免底部界面虚反射对子波的干涉,但没有涉及如何消除炮检点耦合的影响。另外,杨智超等[10]基于双井微测井数据,利用谱比法求取单点Q值,王晓涛等[11]在厚沙漠区采用了单双井微测井等多种采集方法计算近地表Q值。
现有微测井采集方法为井中激发、地面接收方式,井中激发一般采用雷管,激发的地震波频率较高,可以提高初至时间拾取的精度,从而准确反演近地表速度变化。但这种方法用于近地表Q调查时存在炮点和检波点耦合问题,且激发频率越高,耦合问题越严重。本文提出了一种炮检点对称的双激发微测井采集方法,采用电火花激发方式,激发井深度大于低速带厚度,井间的距离约大于激发井深度,检波点等距离(约1~3m)布置在两井之间。计算近地表Q值时可通过对称互换的方法消除炮点和检波点耦合对Q值反演的影响。
1 问题分析
利用微测井资料计算近地表Q值时,如何消除炮检点耦合影响是一个十分关键的问题。图1a展示了一个地下不同深度点激发、地表检波器接收的微测井记录,数据道的炮检点距离从左至右逐渐增加。按照地震波衰减理论,传播距离越长,地震波高频成分衰减越多,频带宽度越窄,而实际记录相反,传播距离长的深度(地下39m处)激发的数据道初至频带宽度(图1b)大于传播距离短的深度(地下1m处)激发的数据道初至频带宽度(图1c)。究其原因,是地下1m处激发点地层疏松、激发耦合条件差[12],而39m处激发点地层压实好、密度大、耦合条件好。因此,炮点耦合对数据频率衰减的影响远大于传播距离的影响,如果计算地层品质因子时不考虑炮点耦合的影响,则会计算出一个负的Q值,不符合常规地震波传播衰减理论。
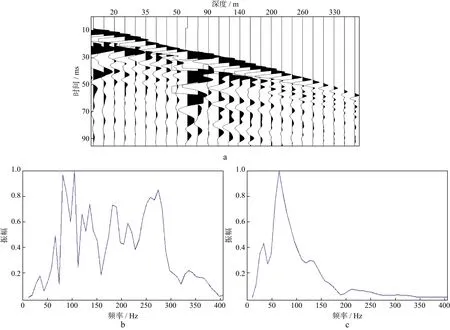
图1 共检波点微测井记录及频谱a 不同深度点激发的共检波点微测井记录; b 深度39m激发道初至频谱; c 深度1m激发道初至频谱
检波点耦合问题在近地表Q值计算过程中同样突出。图2展示了同一个激发点(深度为30m),距离激发井1m到32m布置的近地表不同检波器接收的微测井记录(图2a)及其初至波瞬时谱(图2b),数据道从左至右炮检点距离逐渐增加。初至波瞬时谱采用S变换方法[13]计算,按照地震波传播理论,地震波的高频应该随着传播距离的增加而逐渐衰减,但图2b 所示的初至波瞬时谱变化毫无规律。究其原因,是检波点耦合差异破坏了地震波的衰减规律。近地表检波器的耦合条件好于井中检波器,使用井中检波器接收数据计算Q值时,更需要考虑检波点耦合的影响。
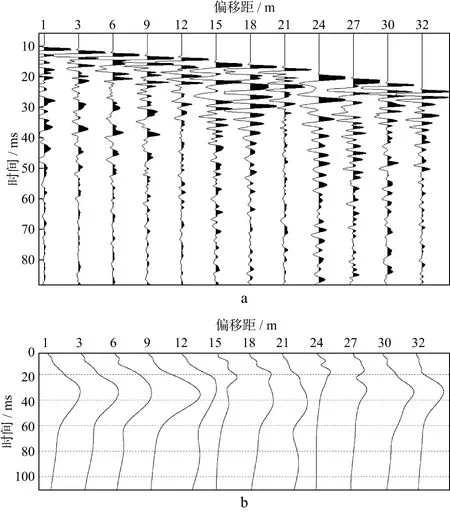
图2 相同炮点不同近地表检波点微测井记录(a)及频谱(b)
2 方法原理
双井激发、地表接收采集方式如图3所示。激发点1和激发点2的深度相同,接收点1与激发井1的水平距离等于接收点2与激发井2的水平距离。
假设激发点1的耦合响应为s1(f),激发点2的耦合响应为s2(f),接收点1的耦合响应为r1(f),接收点2的耦合响应为r2(f),f表示频率,则有:
y11(f)=x11(f)×s1(f)×r1(f)
(1)
y12(f)=x12(f)×s1(f)×r2(f)
(2)
y21(f)=x21(f)×s2(f)×r1(f)
(3)
y22(f)=x22(f)×s2(f)×r2(f)
(4)
式中,y表示受炮检点耦合影响的信号,x表示不受炮检点耦合影响的信号,x和y下标的第1个数字表示激发点序号,第2个数字表示接收点序号。
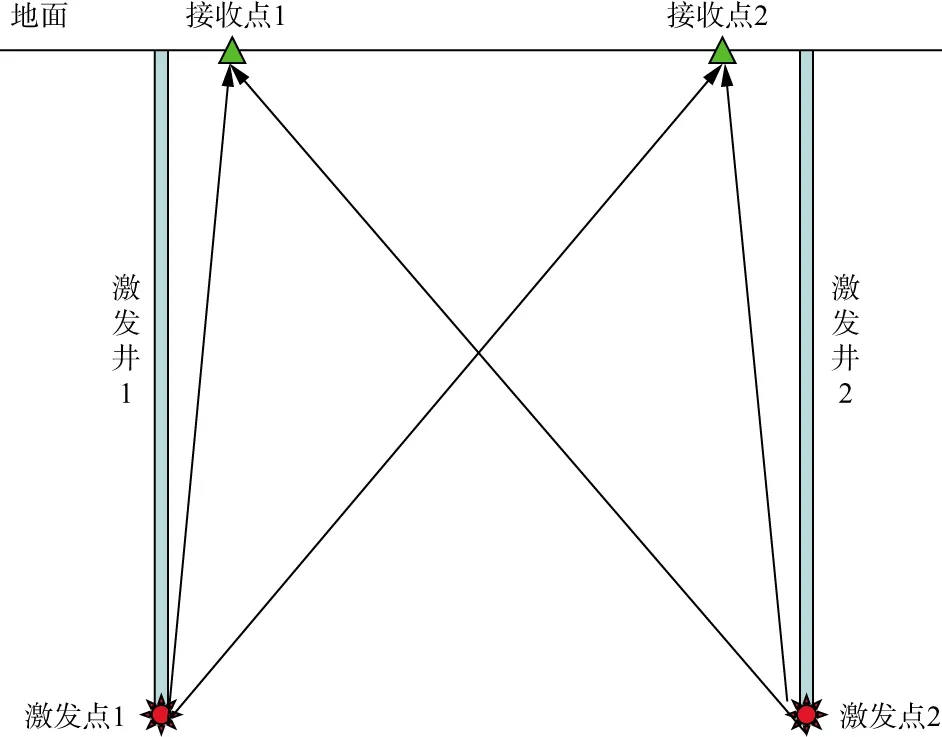
图3 双井激发、地表接收方式
利用谱比法计算Q值时,需要计算衰减前后数据谱比的对数(消除炮点耦合条件的影响),即:
ln[x11(f)]-ln[x12(f)]+ln[r1(f)]-
ln[r2(f)]
(5)
ln[x22(f)]-ln[x21(f)]+ln[r2(f)]-
ln[r1(f)]
(6)
式中:A1(f)是针对激发点1的两个接收点谱比对数,A2(f)是针对激发点2的两个接收点谱比对数。假设激发井1和激发井2之间地层的Q值在水平方向上基本不变,那么其平均谱比对数为:
A(f)=[A1(f)+A2(f)]/2=
{ln[x11(f)]-ln[x12(f)]+ln[x22(f)]-
ln[x21(f)]}/2
(7)
A(f)就是消除了炮检点耦合影响的谱比对数。
实际数据初至波附近的频谱采用S变换方法[13]得到,计算公式为:
(8)
式中:S表示h(t)函数的S变换,f为频率,t为时间,用于控制高斯窗函数在时间轴上的位置。S变换主要用来求取初至时间处的瞬时频谱,它使用频率参数调节时窗长度,频率越低,时窗长度越大,频率越高,时窗长度越小。因此,S变换克服了常规傅里叶变换时窗长度固定不变的缺点,计算出的频谱较好地展示了初至波时刻的频率特性[14]。
用直线A=af+b对计算出的谱比对数的n个数据点(Ak,fk)(k=0,1,…,n)进行回归分析[15-16],得到谱比对数的斜率a,由下式计算地层品质因子Q:
Q=π×t/a
(9)
式中:t为地震波传播时间。
3 应用实例
实际数据采用图3所示双井激发、地表接收采集方式,激发点1的两个接收道记录如图4所示,激发点2的两个接收道记录如图5所示。图4b、图4d、图5b和图5d是用S变换方法计算出来的初至频谱,代表初至时刻的瞬时谱。从激发点1到接收点1的地震波传播距离小于从激发点1到接收点2的传播距离,其频带宽度(图4b)也大于后者(图4d),符合地震波传播衰减规律。从激发点2到接收点1的传播距离大于从激发点2到接收点2的传播距离,但其频带宽度(图5b)大于后者(图5d),不符合地震波传播衰减规律,这主要是受检波点耦合的影响。
如果只用激发点1的两个接收道计算Q值,其谱比对数(图6a)的斜率为0.0092,通过拾取微测井记录的初至起跳时间得到初至时间,两个接收道之间的初至时差为0.00325s,据此求得的Q值为1.1098,小于真实的Q值。这是因为该谱比对数的斜率受检波点耦合的影响偏大,根据公式(9)计算的Q值必然偏小。如果只用激发点2的两个接收道计算Q值,其谱比对数(图6b)的斜率为-0.0058,两个接收道之间的时差为0.00325s,求得的Q值为-1.7603,不符合地震波传播理论。
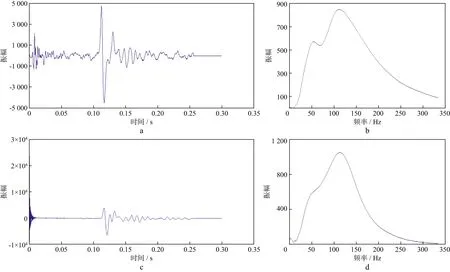
图4 激发点1两个接收点记录及频谱a 接收点1记录; b 接收点1初至频谱; c 接收点2记录; d 接收点2初至频谱
对两个谱比对数求平均(图6c),则消除了检波点耦合的影响。对平均谱比对数数据点进行回归分析,得到谱比斜率为0.0017,两个接收道之间的初至时差为0.00325s,根据公式(9)计算的Q值为6.0059。
图6所示的谱比对数图中,低频部分(小于20Hz)呈现非线性特征,主要原因是炮检点相距较近时出现了近场效应[17],在进行回归分析时应将其剔除。
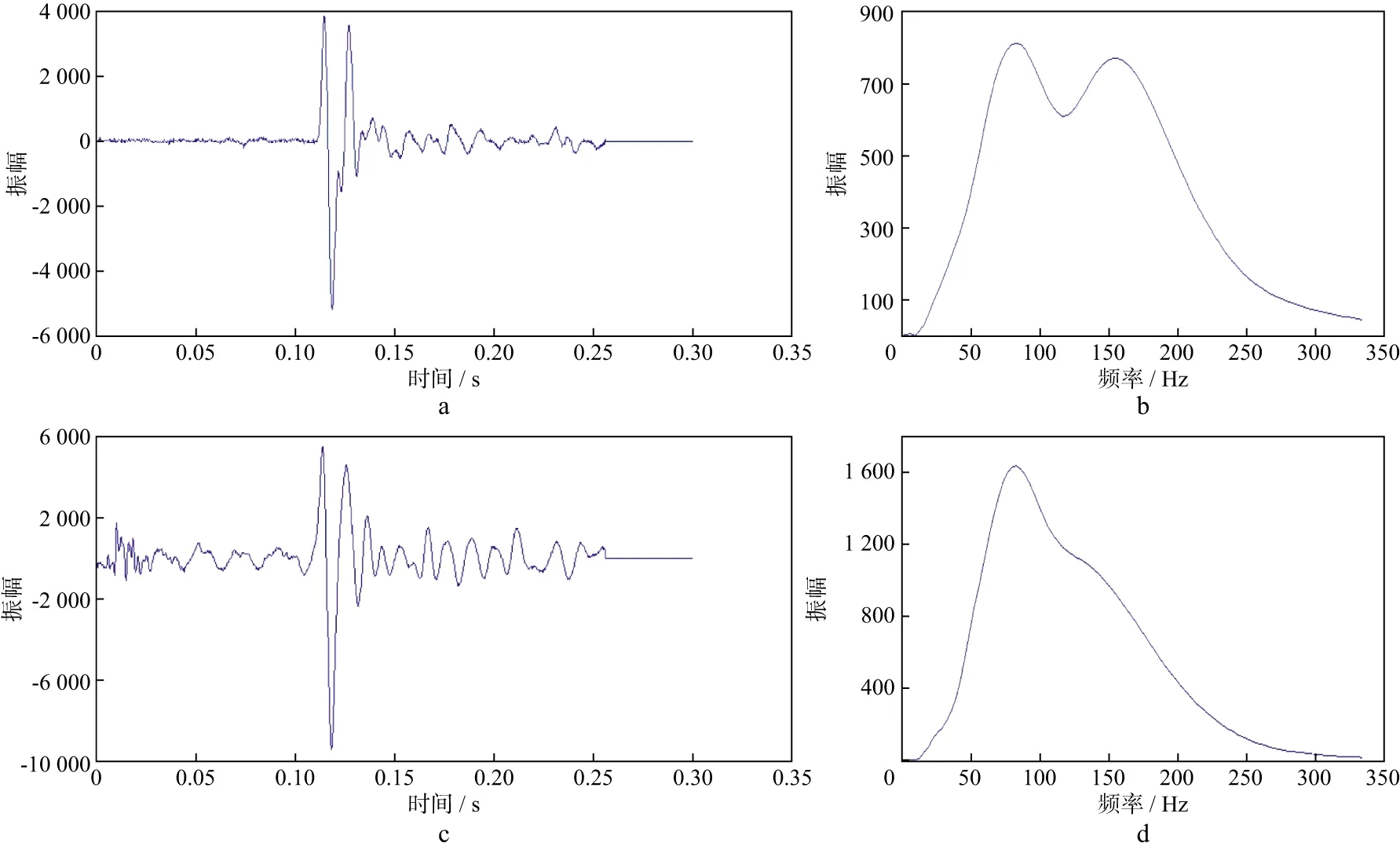
图5 激发点2两个接收点记录及频谱a 接收点1记录; b 接收点1初至频谱; c 接收点2记录; d 接收点2初至频谱
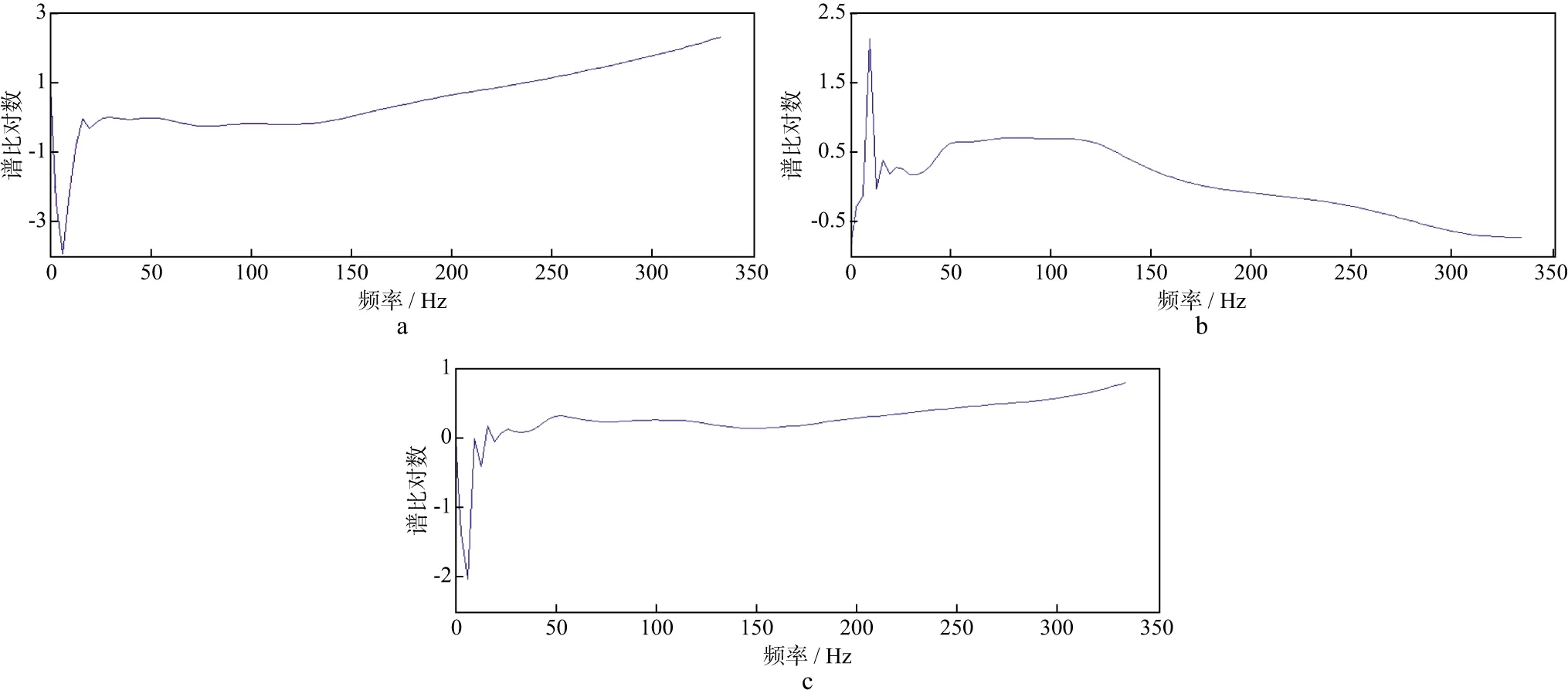
图6 双激发双接收谱比对数a 激发点1谱比对数 ; b 激发点2谱比对数; c 激发点1和激发点2平均谱比对数
为了与常规双井微测井Q采集方法进行对比,在激发井1旁边布置1口接收井,井口和井底各布置一只检波器,仍然在激发点1进行激发(图7)。图8展示了地面(图8a、图8b)和井底(图8c、图8d)接收的记录和初至频谱以及谱比对数(图8e)。可以看出,谱比对数与频率的关系没有出现线性特征,主要原因有两个:①检波器通过重锤下到井中并向井中灌注泥浆后,虽然经过一定时间的沉淀,但仍然无法保障井中检波器的耦合条件,其耦合特征也与地面检波器耦合存在较大差异;②井中检波器与激发点1的距离较近,接收到的信号稳定性较差,尤其是低频端,在计算谱比斜率时需要将低频端的许多数据点剔除,这使谱比斜率的准确性降低了不少。
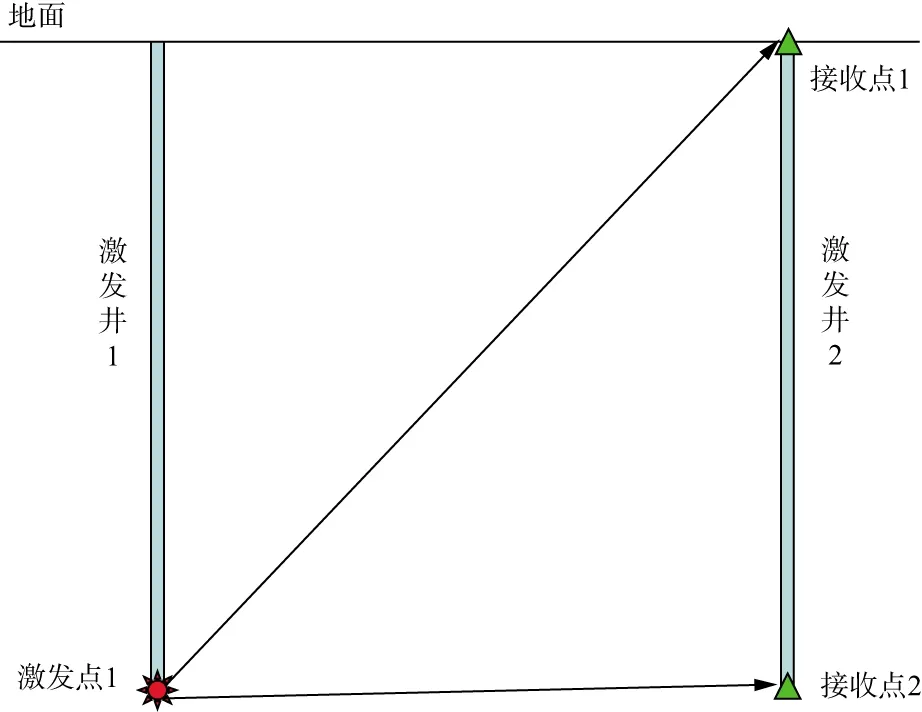
图7 常规双井微测井激发接收方式
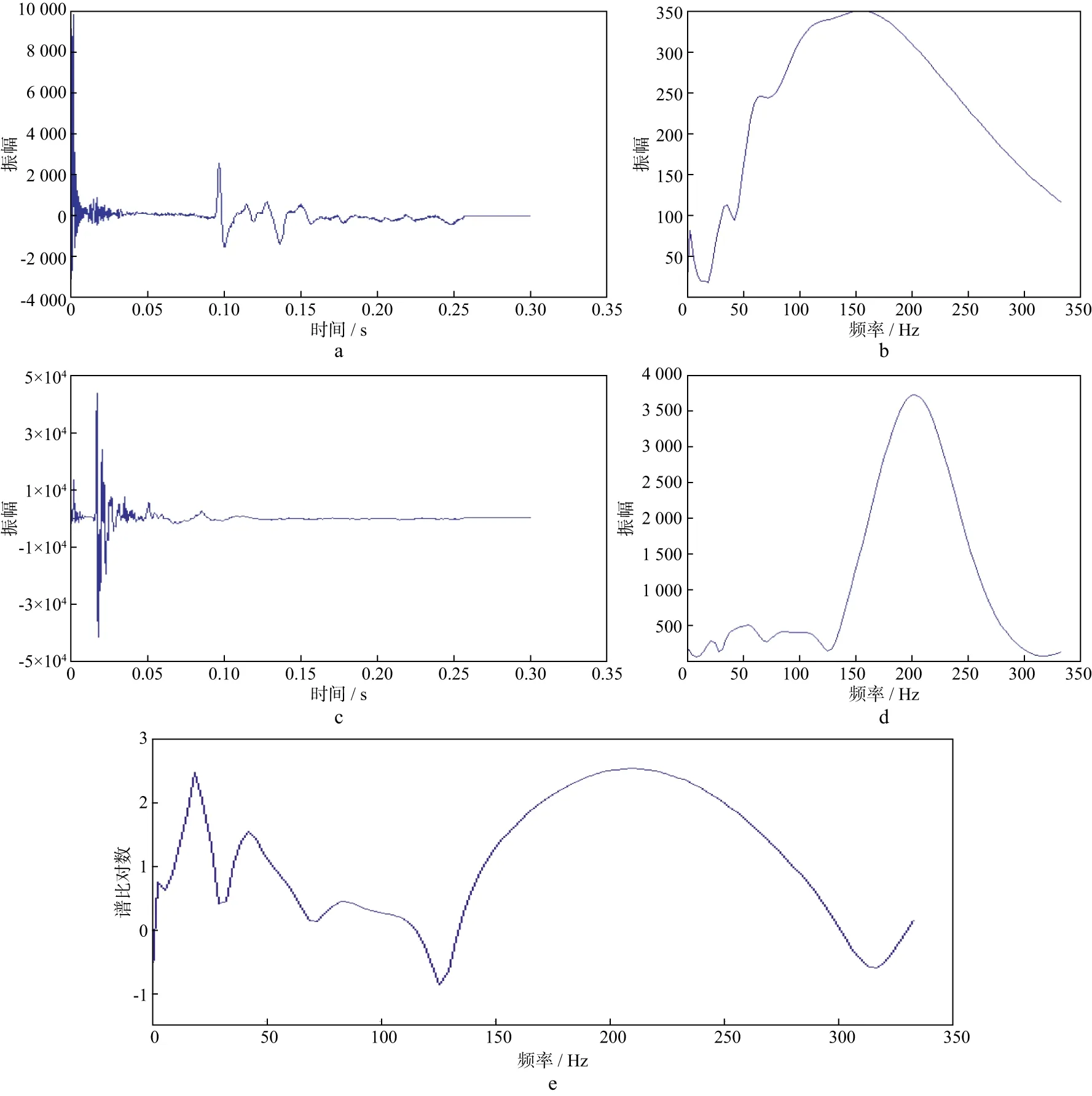
图8 常规双井微测井记录对比a 地面接收记录; b 地面初至频谱; c 井底接收记录; d 井底初至频谱; e 井底与地面记录的谱比对数
由此可见,常规双井微测井Q采集方法得到的数据谱比斜率规律性差,无法准确计算出近地表Q值。另外,井中检波器采集的资料信噪比远低于地面检波器采集的资料(图9),这必然会对近地表Q值计算产生不利影响。
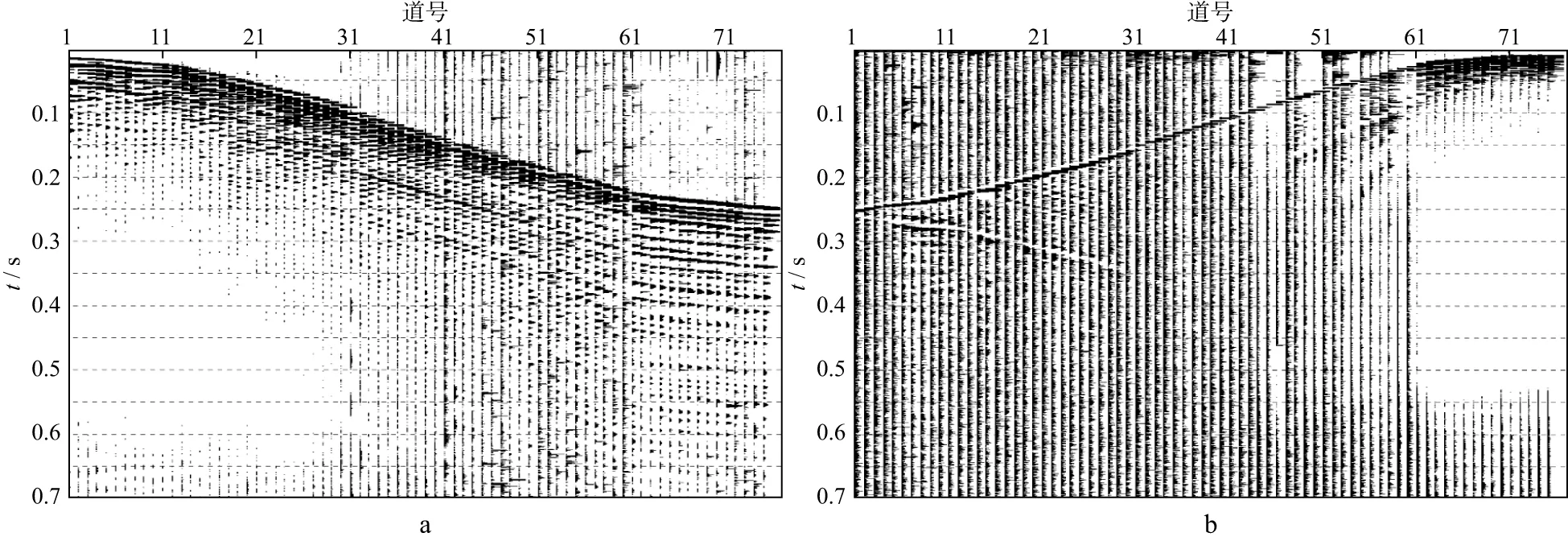
图9 地面检波器(a)与井中检波器(b)资料对比
4 结束语
本文提出双井激发、井间地表布置双接收点,且激发点与接收点对称分布的近地表Q采集方法,通过使用相同炮点、不同检波点的谱比斜率消除了炮点耦合的影响,通过两个激发点的平均谱比斜率消除了检波点耦合的影响,大大提高了近地表Q的采集及计算精度。
在野外数据采集中,可以通过增加激发点与接收点的距离来增加接收信号的稳定性,避免利用回归分析方法计算谱比斜率时大量剔除低频端异常数据点,从而提高Q值计算的稳定性。
需要指出的是,该方法需要假设两个激发井之间水平方向的Q差异性较小,近地表结构变化剧烈时无法满足这一假设条件。
