考虑剪滞效应和剪切变形的曲线箱梁自振研究

兰玮琦，姚激，黄坤

(昆明理工大学 建筑工程学院，云南 昆明 650500)

曲线箱梁因占地面积小、抗扭刚度大、自重轻等优点，在城市桥梁建设中被广泛应用。但是箱型截面的应力分布相比实心截面的更复杂，特别是剪力滞效应。曲线梁桥中，由于曲率的影响，曲线简支梁桥会受到弯曲、扭转、剪力滞及剪切耦合作用，相比于直线梁桥的受力更加复杂。许多学者对曲线箱梁的动力分析进行了大量的研究[1−3]，研究结果表明：剪力滞效应在箱型梁结构的动力分析中，会产生较大影响。

Reissner[4]首次使用能量变分法，建立了闭合矩形箱梁的剪力滞效应微分方程。Chen[5]等人利用能量变分法，推导出简支波纹钢腹板和桁架组合箱梁桥的剪力滞系数实用计算公式。Gyani[6]等人对复合材料悬臂箱梁的剪力滞效应进行分析，推导出悬臂梁的控制微分方程，并进行了求解。潘旦光[7]等人基于模态摄动法，将变高度箱梁剪力滞微分方程组转化为代数方程进行求解，简化了部分复杂箱梁剪力滞系数的计算。蔺鹏臻[8−9]等人分析了抛物线型纵向位移函数中产生的附加轴力，建立了截面应力自平衡的纵向位移函数，对剪力滞效应中翼缘板纵向位移函数的选取有重要参考价值。时元绪[10]等人将箱梁的翼缘板简化为一定刚度弹簧连接的弹性体，结合变分原理，推导出不同的纵向位移函数，并带入剪力滞效应微分方程进行求解，将其计算结算与实测值和有限元模型计算结果进行对比。卢海林[11]等人基于能量原理，推导出悬臂箱形梁的剪力滞系数计算公式，揭示了剪力滞效应沿曲线箱梁全跨的分布规律。实际桥梁工程中，其动力特性较为复杂，学者们进行许多研究。蔡恒[3,11−12]等人考虑剪力滞效应对自振频率的影响，运用能量变分法，推导出不同翼缘板纵向位移函数的微分方程，并利用伽辽金法进行近似求解。陈玉骥[14−15]等人分别假设不同的翼缘板纵向位移函数，采用能量变分原理，推导出弯、扭、剪力滞效应耦合作用下的几何非线性控制方程。马驰[16]等人结合能量变分原理，考虑剪力滞效应和翼缘板不同材料的属性，推导出箱梁的微分方程。但这些研究成果都没有考虑到剪切变形的影响。而曲线箱梁在弯、扭耦合作用下出现破坏，是因为箱梁腹板薄弱，抗剪能力不足。所以在结构动力特性分析中，对剪切变形的考虑十分必要。针对腹板的剪切变形和剪力滞后双重效应作用下，结构自振频率的研究较少。因此，作者拟基于能量变分原理和哈密顿原理，推导出弯、扭、剪力滞效应和剪切耦合作用下简支曲线箱梁的自由振动微分方程，并根据假设模态法对微分方程分离参数进行近似求解。依据本研究推导公式，利用MATLAB 编程进行求解，得到自振频率，并将其与ANSYS 有限元模计算结果进行对比分析。

1 振动微分方程及边界条件

1.1 基本假定

分析曲线箱梁自由振动，需要进行假定：①无阻尼影响，材料处于线弹性阶段；②箱梁翼缘板不满足平截面，箱梁腹板满足平截面；③翼缘板纵向位移函数沿板宽按三次抛物线分布；④忽略翼缘板平面外的横向应变和剪应变[8]。

简易曲线箱梁截面示意图如图1 所示，坐标轴采用曲线坐标轴，x 轴为顺桥向，y 轴指向圆心，z轴为竖向。所有参数取值与坐标轴的方向箭头指向一致为正，相反则为负。在图1 中，h1、h2、h3、h4分别为顶板厚度、悬臂板厚度、底板厚度、腹板厚度；b1、b2、b3、b4分别为顶板宽度、悬臂板宽度、底板宽度、腹板高度。

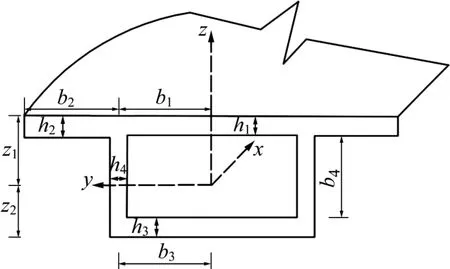
图1 曲线箱梁截面示意Fig.1 Section of curved box beam

假设翼板的纵向位移为：

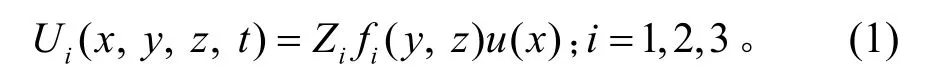
其中，

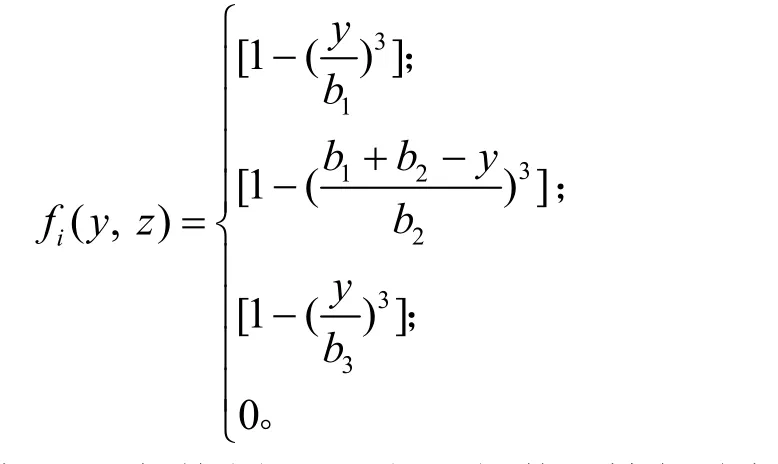
式中：u(x)为翼缘板和腹板之间剪切转角最大值；fi(y,z)为纵向位移分布函数；Zi为上下翼缘板距形心的距离。

式(1)中，当i=1 时，为顶板的；i=2 时，为悬臂板的；i=3 时，为底板的；i=4 时，为腹板的。

在弯扭耦合作用下，箱梁的正应变为：

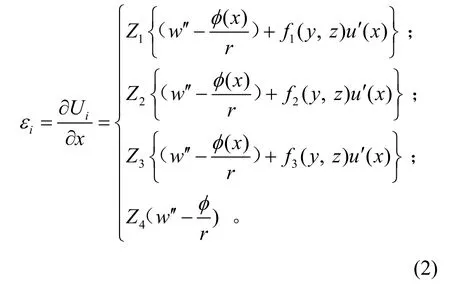
箱梁的切应变为：

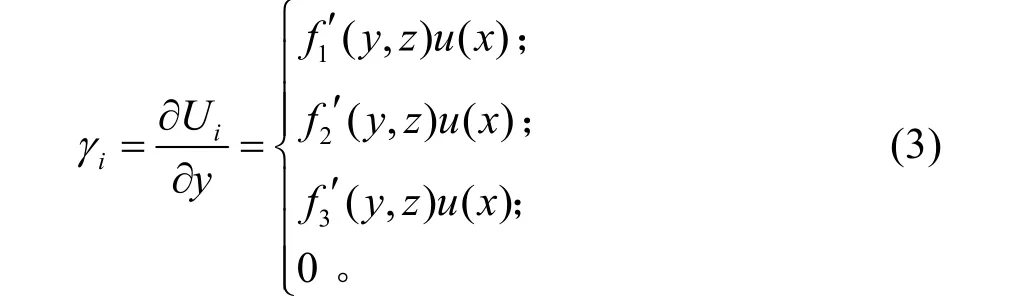
1.2 箱梁的应变能和动能

顶板弯曲应变能为：

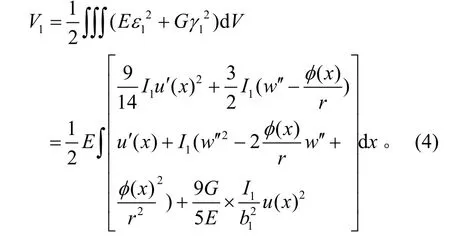
式中：E 是弹性模量；G 是剪切模量。

同理可得，悬臂板弯曲应变能：

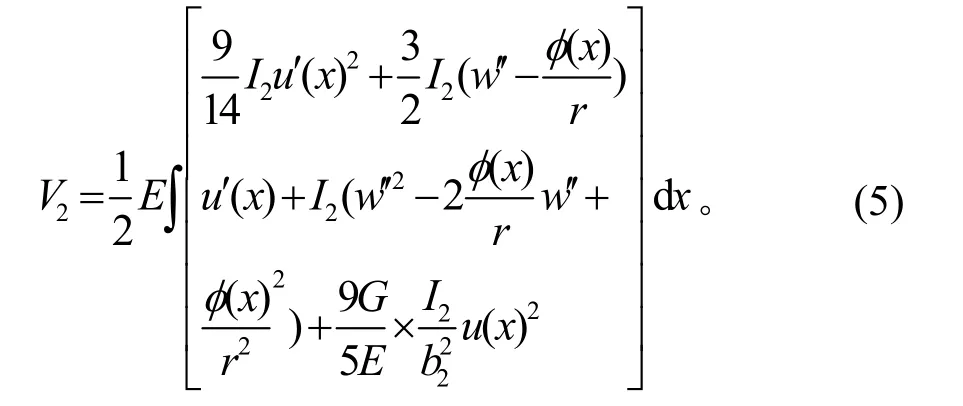
底板弯曲应变能为：

腹板弯曲应变能为：

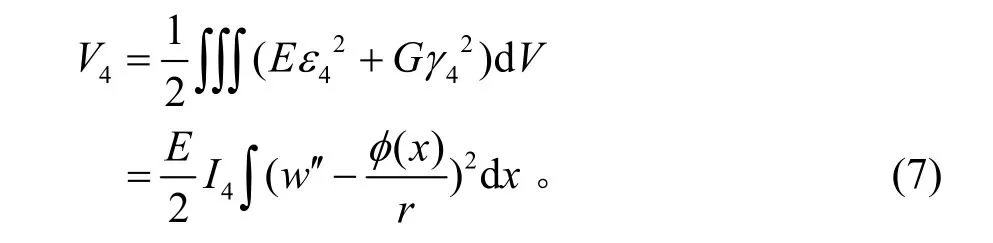
箱梁腹板的剪切应变能为：

式中：A4为腹板面积；θ 为截面转角。

自由扭转应变能为：

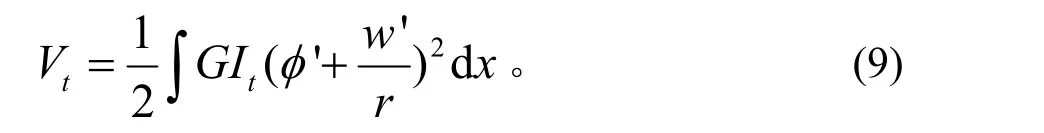
式中：It为桥梁抗扭惯性矩；

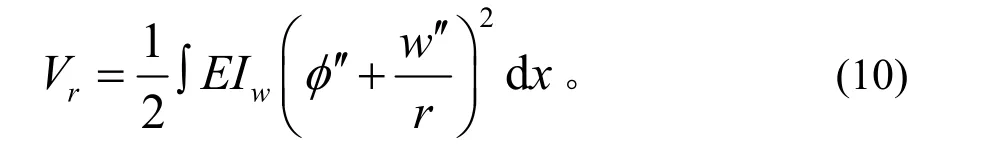
式中：Iw为桥梁扇形惯性矩；

整理可得，箱梁总应变能为：

式中：Is为翼缘板惯性矩，Is1为翼缘板广义惯性矩。

箱梁的动能（仅考虑竖向振动）为：

式中：m 为单位长度质量，t 为时间。

外荷载所做的功为：

式中：P(w, t)为外荷载。

1.3 振动微分方程及其边界条件

由于自由振动，无外荷载做功，可根据哈密顿原理得到：

式中：t1、t2为积分的起始时间和终止时间。

整理得到曲线箱梁的振动微分方程为：

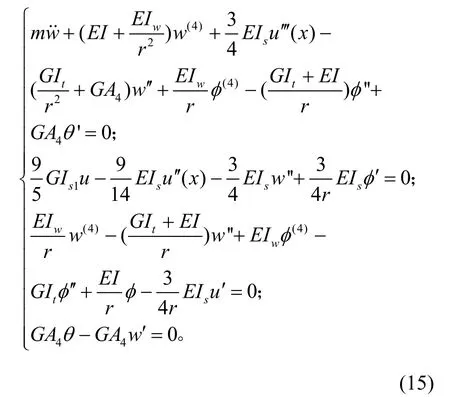
其中，

式中：I 为箱梁截面惯性矩，I=I1+I2+I3+I4。

2 自振频率的计算

由于弯、扭、剪切及剪力滞效应耦合的偏微分微分方程求解难，因此，利用假设模态法对其分离变量近似计算。假设曲线箱梁的位移场函数为：

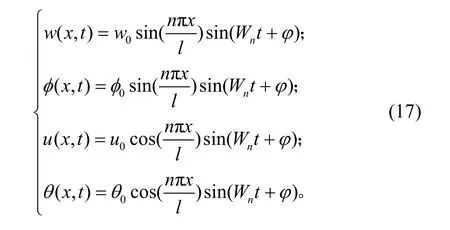
式中：Wn为振动角频率；φ 为振动的初相角；n 为振型阶数；l 为跨径；w0为竖向位移幅值；0φ 为扭转角幅值；u0为剪切转角幅值；θ0为转角幅值。

将式（17）带入式（15），化简可得到：

式（18）是关于w0、u0、0φ 、θ0的齐次方程组，其有意义的条件是方程组有非零解，即系数行列式为零。其计算式为：

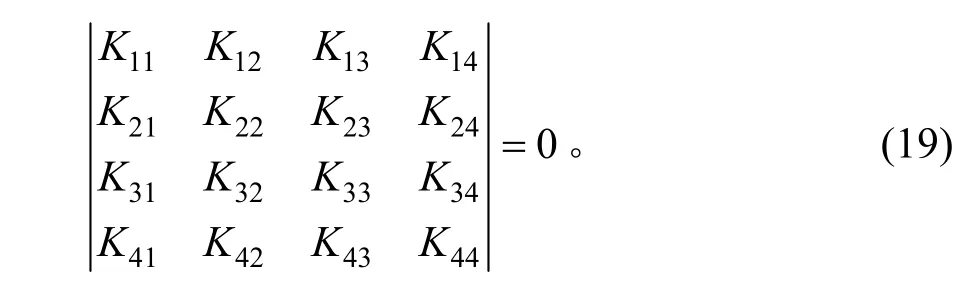
其中，

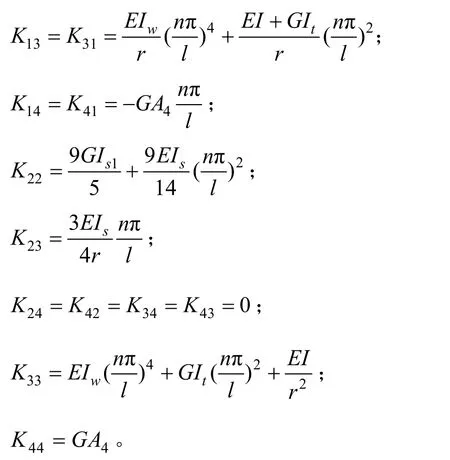
可以求出曲线箱梁的自振频率为：

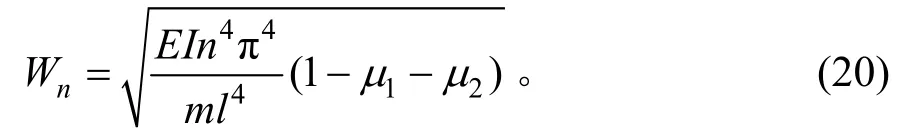
式中：μ1为剪滞效应影响系数；μ2为剪切效应影响系数。

其中，a1=l2/r2；a2=Iw/Il2；a3=GIt/EI；a4=Is/I；a5=GIs1/EI；a6=GA4/EI；D1=9 a24/16；D2=π2a2+a3+1；D3=π4a2+π2a3+a1；D4=9a4/14+9a5l2/5π2。

当r→∞时，曲线箱梁自振频率与文献[17]相同。

当μ1、μ2为0 时，即不考虑剪力滞效应和剪切变形，箱梁的自振频率与初等梁理论的简支梁自振频率相同为：

表明：考虑剪力滞效应和剪切变形推导出的公式具有一定的通用性。

3 算例

采用简支箱型截面梁为例，具体尺寸标注如图1 所示，几何参数和材料参数为：弹性模量E 为3.5×1010Pa，泊松比为0.3，b1=2 m，b2=1.5 m，b3=2 m，b4=2 m，h1=0.3 m，h2=0.3 m，h3=0.3 m，h4=0.3 m，密度=2 500 kg/m3，截面面积A=4.59 m2。根据式(20)，利用MATLAB 计算的值与ANSYS 软件计算结果进行对比验证。模型如图2 所示。在ANSYS 建模分析过程中，采用solid185 单元，自底向上的建模方式，边界条件为简支。其计算结果见表1。

图2 ANSYS 模型Fig.2 The ANSYS model

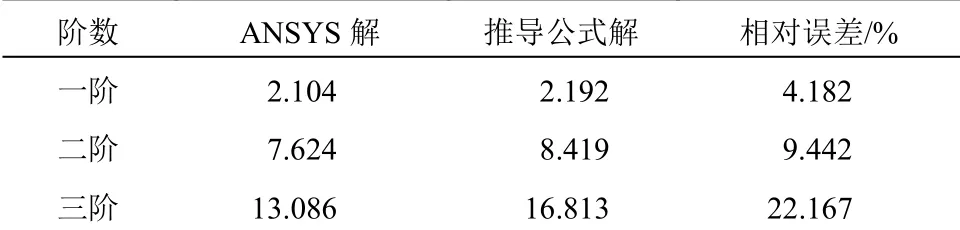
表1 自振频率计算结果表Table 1 Calculation result of natural frequency

由表1 可知，推导公式的求解值大于ANSYS有限元计算值。在振型阶数为一阶时，相对误差较小，为4.182%；在振型阶数为三阶时，相对误差较大，为22.167%。当振型阶数为一阶和二阶时，振型周期以平动为主；当振型阶数为三阶时，横向振动和箱梁畸变、翘曲变形对振型周期的参与系数变大。由于本研究只考虑了竖向弯曲振动，未考虑对于横向振动、箱梁畸变和翘曲变形，导致推导公式所得结果与ANSYS 结果出现较大误差。表明：在振型阶数为一阶时，该方法得到曲线箱梁的自振频率，精确度较高且有一定程度的实用性。

利用MATLAB 编制程序，分别计算跨径30,35,40,45,50 m 和曲率半径为50,100,150,200 m 时20 种工况曲线箱梁的自振频率、剪滞效应贡献度及剪切变形贡献度。

3.1 跨宽比

采用控制变量法，对同一曲率半径的不同跨径曲线箱梁的ANSYS 计算结果和推导公式解进行统计，结果如图3,4 所示。从图3 可以看出，自振频率随着跨宽比的增大而降低。当跨宽比为4.29 时，一阶自振频率为5.096 9 Hz；跨宽比为7.14 时，一阶自振频率为2.104 3 Hz。表明：跨宽比越大，桥梁结构的相对刚度越低，柔度增加使得自振频率降低。从图4 可以看出，剪力滞效应贡献度随着跨宽比的增大而增加，但剪切效应贡献度随着跨宽比的增大而降低。当跨宽比为4.29 时，剪力滞效应贡献度和剪切变形贡献度分别为10.48%和13.62%；当跨宽比为7.14 时，剪力滞效应贡献度和剪切变形贡献度分别为22.42%和13.67%。表明：在跨宽比较小时，剪切变形对自振频率的影响较大，使得曲线箱梁的相对刚度减小，剪力滞效应对自振频率的影响较小。但剪切变形贡献度约为14%时，剪力滞效应贡献度随着跨宽比的增大而大幅度上升。

图3 跨宽比对自振频率的影响Fig.3 The influence of span-width ratio on natural frequency

图4 剪力滞效应和剪切变形贡献度Fig.4 The contribution of shear lag effect and shear deformation

3.2 曲率半径

同一半径3 种不同曲率的ANSYS 结果和推导公式解如图5,6 所示。

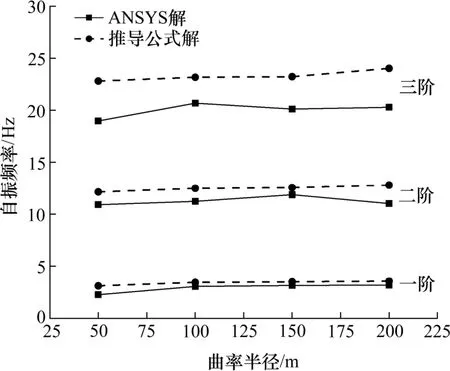
图5 曲率半径对自振频率的影响Fig.5 Influence of curvature radius on natural frequency

图6 剪力滞效应和剪切变形贡献度Fig.6 Contribution of shear lag effect and shear deformation

从图5 可以看出，自振频率随着曲率半径的增大而增加，但是增加幅度不大。当曲率半径为50 m时，一阶自振频率为2.259 3 Hz；当曲率半径为200 m 时，一阶自振频率为3.175 4 Hz。从图6 可以看出，曲率半径越大，剪力滞效应贡献度减小，剪切变形效应贡献度小幅度减小，大约稳定在14%。当曲率半径50～100 m 时，剪力滞效应贡献度急剧减小，从29.73%降至15.3%；当曲率半径100～200 m时，剪力滞效应贡献度从15.3%下降到9.5%。表明：曲线箱梁的剪切变形对刚度的影响，不完全取决于曲率半径的变化。剪力滞效应对刚度的影响，会因为曲率半径的增大而减小。因为曲率半径的增大，会导致曲线箱梁的应力分布接近于直线箱梁。此时，弯扭耦合作用程度的减小，引起剪力滞效应不明显，进而使得剪力滞效应对相对刚度的影响减弱，从而导致自振频率有小幅度增加。

5 结论

通过对简支曲线箱梁的自振特性分析，得到的结论为：

1) 在振型阶数为一阶时，推导公式的计算值与ANSYS 有限元的计算结果较为吻合。表明：该推导公式具有一定的通用性和准确度。

2) 剪切变形对曲线箱梁自振频率的影响随着跨宽比的升高和曲率半径的增加而减弱。但是剪切变形贡献度变化幅度不大，大约为14%。

3) 剪力滞效应对曲线箱梁自振频率的影响随着跨宽比的降低和曲率半径的增大而减弱。但是曲率半径在50～100 m 时，剪力滞效应对自振频率的影响急剧减小，剪力滞效应贡献度在15%～30%；曲率半径在100～200 m 时，剪力滞效应贡献度在10%到15%。

4) 曲线箱梁的自振频率，会随着跨宽比的升高和曲率半径的降低而降低，主要取决于跨宽比的影响。

本推导公式只考虑了竖向弯曲振动，对于横向振动、箱梁畸变和翘曲变形的分析，有待进一步地研究。