英语环境下预选机制投资组合优化实验研究

翟静　栗方　郭浩　梁娜　严洪轩

[摘 要]投资组合优化问题是指为了同时获得最大的整体回报和最小的整体风险，选择不同的资产进行投资。目前，我国许多中小企业家在国际化投资中，找到一个最好的投资组合方案问题的复杂性往往随着可供选择资产数目的增多而变大，而且语言障碍也是一大难题。为了给出英语环境下大规模投资组合的最优解，基于智能优化算法提出了两种考虑个别资产收益和风险的资产预选方法。文章借助于粒子群优化算法对资产进行优化选择，并设计了4组不同设置的实验。从4组实验的数据可以得出，所提出的预选择方法不但确保了优化问题的准确度，同时通过人工智能技术给投资者提供国际化投资组合建议。

[关键词]粒子群优化算法;预选机制;投资组合策略

[DOI]10.13939/j.cnki.zgsc.2020.02.032

1 投资组合优化的前景

国际环境下的投資者需要分析若干个资产的相关英语文件，进一步从一个庞大的可能性集中形成一个单一的投资组合方案，以便最大限度地提高回报和减少风险。投资组合优化算法可以辅助每一个投资者找到一个最适合的投资组合策略。正如“商业周刊”所述，对付风险最好的武器就是用不相关或者负相关的资产[1]，因为几个这样的资产合并在一起，组合后方案的总体风险可能小于单一资产的风险[2]。因此，找到一组最合适的投资组合方案获得了投资者和学者的广泛关注。在1952年出版的Markowitz的投资组合选择理论使投资组合优化得到了重大突破[3]。随着可供选择的资产数量大量增加，优化问题的复杂程度和优化的计算时间将会不可想象[4]。在本文中，笔者考虑了中国沪深股票市场近五年的日线数据，使用最多的股票数量是1000只。为了实现大规模投资组合优化，本文提出了两种资产预选流程，使得要考虑的资产数目可以增加到几千个或更多，本文把粒子群优化算法（PSO）作为优化工具，测试了预选过程的有效性。

2 使用MATLAB对股票数据进行优化

2.1 股票数据的获取

本文选用中信证券客户端下载股票数据，此方法可以无限制批量下载股票的历史数据，生成的CSV文件可直接通过MATLAB函数导入，也便于后期的数据处理。

2.2 资产收益风险的求解

2.2.1 对每个单个资产进行收益风险评估

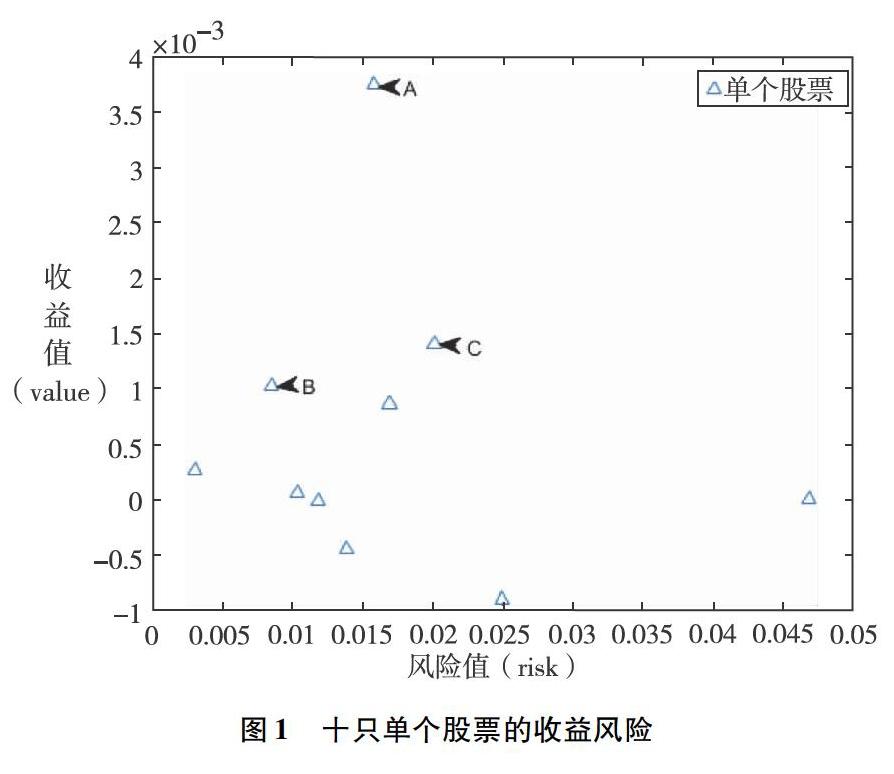
在已知投资组合中各资产权重的情况下（在单个资产优化过程中，每一个单个资产都被当作是一个投资组合，故所有资产的权重全为1），在MATLAB中可以使用PORTSTATS（ ）函数计算投资组合的收益与风险，为了测试这个函数，本文随机选取了10只沪深日线的股票进行了绘制，绘制结果如图1所示。

从图中可以看出，资产A是最优的单个资产，其次是资产B、资产C。如果投资者想要从这十只股票中选取三只股票进行投资，那么此方法下最优的投资组合方案即为[资产A，资产B，资产C]。

2.2.2 对两个资产进行组合

本文第一节中提到，对付风险最好的武器就是用不相关或者负相关的资产，因为几个这样的资产合并在一起，组合后方案的总体风险可能小于单一资产的投资组合风险。如若已经计算得出总体中所有股票的收益风险值，MATLAB可以调用PORTSTATS（ ）函数来模拟组合后的收益与风险值，此次的各资产权重不再设置为1，而是按照约束处理编码方式进行设置， 为了展示组合后的方案效果，从上述提到的十只单个股票中选择了两个负相关的资产，并且标记出了组合后的收益风险值，结果如图2所示。

从图中不难发现，资产B与资产C呈负相关，当这两种资产组合后可以大幅度地提高资产价值，并降低组合后的资产风险值。如果对所有的两两资产进行组合评估，就能得到所有资产中最优的投资组合方案。由于组合后的资产风险随着组合资产数量的增加而增加[5]，故本文只考虑两两资产组合的情况。

3 基于预选方法的大规模投资组合优化

资产选择过程的方案是观察到每项资产有自己的风险值和回报值，这些风险和回报值可以绘制出来，也可以接受非线性排序过程[6]，同时过滤掉大量不良资产。基于这些观察，本文提出了两种资产预选流程，具体如下。

资产预选流程M-1：很容易理解，好的单一资产（具有高回报和低风险的股票）可能对最终优化的投资组合方案具有贡献。因此，在资产预选流程M-1中，根据单个资产的收益和风险使用粒子群算法来选择资产。在这个过程中，每个资产都会被看作是一个投资组合，并且这些资产在预选过程中会对其进行价值排序。选择基于分配给每个资产的价值等级，直到所选资产的数目达到预定义的（用户定义的）数量。虽然M-1的概念很简单，但是它对于减少不良资产是非常有效的，并且对最终的投资组合方案具有比较大的贡献。

资产预选流程M-2：虽然资产预选流程M-1简单有效，但是在需要高绩效的投资组合方案时，仅考虑个别资产的风险和回报是远远不够的，因为两个负相关的资产也有可能根据他们负相关的程度降低风险，从而提高投资组合的总体价值。因此，在资产预选流程M-2中，考虑了单个资产和具有负相关属性的资产对。图2显示了如何使用资产预选流程M-2选择资产。假设希望从10项资产A-J中选择3项资产，所有的资产都会根据其回报值和风险值进行标记。在10项资产中，假设只有B资产和C资产呈负相关，由B资产和C资产可以得到一组投资组合，称为BC，这一组合将会对最终的投资组合方案提供最大的贡献。很明显，BC点占资产C的主导地位。因此，资产A、B和C将被选为最佳的3个资产。

4 实验与结果

4.1 实验设置

为了测试所提出预选方法的可行性，本文下载了1000只中国沪深股票市场的1000天收盘价（从2014年7月7日起），并将其作为模拟历史股票的数据。对于所提出算法进行实验，具体的实验内容和设置如下。

实验E-1，不使用预选方法，对1000只股票进行收益风险计算，使用传统办法（冒泡排序法）选择最有价值的3只股票。

实验E-2，不使用预选方法，对1000只股票进行收益风险计算，使用粒子群优化算法优化出最有价值的3只股票。

实验E-3，使用资产预选流程M-1从1000只股票中预选出100只最有价值的股票，再使用PSO算法从中选出3只最优股票。

实验E-4，使用资产预选流程M-1从1000只股票中预选出100只最有价值的股票，再使用资产预选流程M-2和PSO算法从100只股票中优化出3只最优股票。

4.2 实验结果

4.2.1 实验结果展示

实验E-1、E-2结果如图3所示，这两个实验的结果图（收益风险图）相同，得到的三只最优股票相同，但是运算时间不同。实验E-3、E-4的结果分别如图4、图5所示，实验所得数据如表1所示。

4.2.2 实验结果分析

通过对四组实验的结果进行分析，可以得出这样一个结论。

对比实验E-1和实验E-2可知，粒子群优化算法在计算速度方面有很大的提高，在确保准确性的情况下，大大缩短了计算的时间，由此可见粒子群算法在处理大规模优化问题的时候，能起到提高计算效率的功效。通过对实验E-2与实验E-3的实验结果分析，可以证实资产预选流程M-1在资产预选时可以过滤掉大量不良资产，从而减少优化问题的维度，缩短优化过程的时间。实验E-4是在综合了粒子群优化算法和资产预选流程M-1后，对筛选出的优良资产再次进行优化，此次试验采用资产预选流程M-2对筛选后的100只优良股票进行负相关组合，对所有的两两股票进行模拟组合投资，选出最优的两只股票作为最终投资组合方案供投资者选择。

为了证明预选过程的有效性，图3和图4分别绘制了无（1000只股票）和有（100只股票）资产预选流程（M-1）的收益风险图。从这两张图中可以看出，在应用预选方法M-1后，不良资产大幅度减少。预选过程去除了不良股票，并保留那些可能对投资组合有贡献的股票。该方法不仅减少了计算的时间，而且提高了求解的质量，更能提高算法的计算效率。

從图4和图5中还可以看出资产预选方法2（M-2）比资产预选方法1（M-1）的效果好，其原因是显而易见的。M-2同时考虑单只股票（高回报、低风险）和负相关对，而M-1只考虑单只股票。负相关对能进一步提高投资组合方案的质量。然而，当精度要求不高时，M-1仍然有用，因为这种方法比M-2快，更能快速获得有价值的股票。

综合所有实验的结果，使用预选方法的优势变得更加明显。资产预选流程M-1简单轻巧，能大幅度过滤掉不良资产，计算时间少。资产预选流程M-2虽然在计算时间上花费比较多，但是能找到最优的股票负相关对，找到最好的投资组合方案。

5 结论

本文介绍了一种解决国际环境下的投资组合优化问题的有效方法。提出了两种不同的资产预选流程。实验结果表明，由于资产预选程序，特别是资产预选流程M-2，即考虑单一资产和负相关对的选择过程，产生的有效投资组合的质量显著提高。本文提出的优化方法对投资者英语环境下国际化投资具有很强的辅助性。

参考文献：

[1]林春艳.多种环境下的证券投资组合优化及其应用[D].大连：大连理工大学， 2004.

[2]丁晓东，肖琳灿，罗和治.带边际风险控制的投资组合问题的半定规划松弛[J]. 浙江工业大学学报，2017（1）：68-72.

[3]李善民，徐沛.Markowitz投资组合理论模型应用研究[J].经济科学， 2000（1）：42-51.

[4]徐金发，黄亮华. 基于可变相关系数的投资组合研究[J].技术经济与管理研究，2004（5）：60.

[5]郭晓霞.我国证券市场中资产数量与组合风险关系的实证研究[D].保定：河北大学， 2006.

[6]张兆印，耿学新.非线性数据快速排序算法的BASIC实现[J].黑龙江大学自然科学学报，1989（2）：47-48.