基于ANSYS参数化语言的密封舱结构优化

姚远明，赵启林*，施丽铭，邓宇华，范柄辉

(1. 南京工业大学机械与动力工程学院，南京 211800； 2. 北京空间飞行器总体设计部，北京 100094； 3. 江苏狄诺尼信息技术有限责任公司，南京 210000)

1 引言

加筋薄壳结构的航天器密封舱由蒙皮和横纵肋条组成，相较早期航空航天常用的杆板结构，既有足够的局部弯曲刚度，又能参加总体承力，极为广泛地应用于各种航天器结构[1],如PROTON-M运载火箭的结构支承舱[2]。

目前加筋薄壳结构优化设计已有不少研究。毛佳等[3]建立了轴向载荷作用下正置正交薄壁加筋圆柱壳结构优化设计的数学模型和有限元分析模型，应用 Ansys 软件进行优化计算，讨论了外载荷、材料屈服极限对优化设计的影响以及结构参数对薄壁加筋圆柱壳结构的临界载荷和屈曲模式的影响；孙志彬等[4]提出了一种金属加筋薄壁圆台结构的二级布局优化方法，算例结果表明，该方法简单且优化效率高[4]；舒恪晟[5]针对机身加筋壳结构布局优化设计问题，首先采用一种基于二次曲线的参数化建模方法来建立机身几何模型，然后提出一种基于等效模型的简化模型的方法，实现了加筋壳结构的快速化结构布局优化设计。加筋薄壳结构的优化一般选择较少数量的设计变量，如舒恪晟[5]在机身加筋壳结构的优化中，只抽取机身的一部分加筋壳结构来进行优化，并且假设桁条、隔板宽度和腹板高度之间存在倍数关系。采用较少数量的设计变量，主要是为了提高优化效率，防止优化结果陷入局部最优解，但是较少的设计变量无法满足精细化设计的要求，对目标改善有限。但若是增加过多的设计变量，虽然满足精细化设计要求，增加了找到最优解的可能性，但同时也会使优化算法搜索困难，容易陷入局部最优解。

针对该矛盾，本文结合实际工程，按截面形状和应力状态对肋条进行分组，提出4种分组方案来设置不同数量的设计变量；通过研究设计变量数量对密封舱优化迭代过程、优化结果的影响规律，来确定最合适的设计变量数，使得优化结果既满足精细化设计的要求又缓和优化算法对大规模设计变量的搜索困难。

2 基于ANSYS的优化设计步骤

ANSYS的优化和数学规划法一样，命令流中主要包含3大优化变量：设计变量X、状态变量和目标函数Y。

通常ANSYS的优化流程如下：

1)生成循环所用的分析文件，包括参数化建立模型、求解、提取并指定状态变量和目标函数；

2)在ANSYS数据库里建立与分析文件中变量相对应的参数；

3)进入OPT，指定分析文件(OPT)；

4)声明优化变量；

5)选择优化工具或优化方法；

6)指定优化循环控制方式；

7)进行优化分析；

8)查看设计序列结果(OPT)和后处理(POST1/POST26)。

优化数据流向见图1。

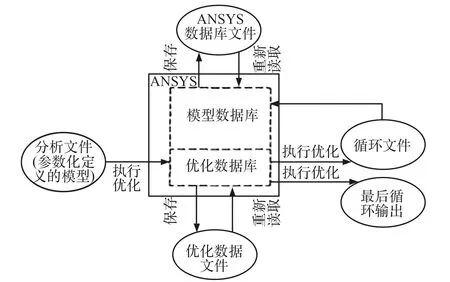
图1 优化数据流向Fig.1 Optimization data flow

本文采用ANSYS提供的零阶算法进行优化。该算法首先通过对目标函数添加罚函数，将问题转化为非约束的优化问题，然后用曲线拟合来建立目标函数和设计变量之间关系来实现逼近，每次优化循环生成一个新的数据点。这是一个完善、通用的方法，可以有效地处理大多数的工程问题[6]。

3 参数化建模

密封舱基本构型为球形，如图2所示，球体由上、下蒙皮、舱门以及横纵肋条构成。蒙皮、肋条均采用铝合金，为方便后续对肋条进行分组，对肋条进行命名，如图3、4所示。

图2 密封舱结构Fig.2 Structure of capsule

图3 纵肋Fig.3 Longitudinal rib

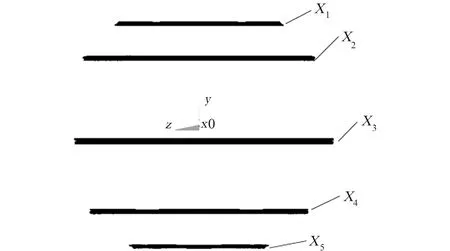
图4 横肋Fig.4 Annular rib

利用ANSYS-APDL语言对密封舱模型进行参数化模型。根据密封舱结构和受力特点，蒙皮选用SHELL181单元，横纵肋选用BEAM188单元进行建模。由于密封舱的几何形状较为规整，对舱体部分采用映射网格划分，对上舱门、侧舱门附近采用自由网格划分，划分的网格形状为四边形网格，建立的有限元模型如图5所示。整个密封舱结构共有40 580个节点，40 607个单元。

图5 密封舱有限元模型Fig.5 Finite element model of capsule

选取特定工况施加荷载，并将各荷载乘以相应的荷载安全系数，详见表1。密封舱上各设备分布情况为：设备1的质量为180 kg，安放在横肋X5上；设备2的质量为100 kg，位于模块顶端，安放在对接框上表面；设备3的质量为100 kg，安放在横肋X2上；其他设备共250 kg，质量均布在各加强筋上。上述各设备质量将乘以惯性荷载及安全系数，以均布荷载的形式作用在相应部位。横肋X4为固接。

利用ANSYS solution模块进行求解，并提取蒙皮节点最大应力、肋条的最大轴向应力、稳定性特征值系数以及密封舱总质量，以便为后面的优化提供目标函数及状态变量。

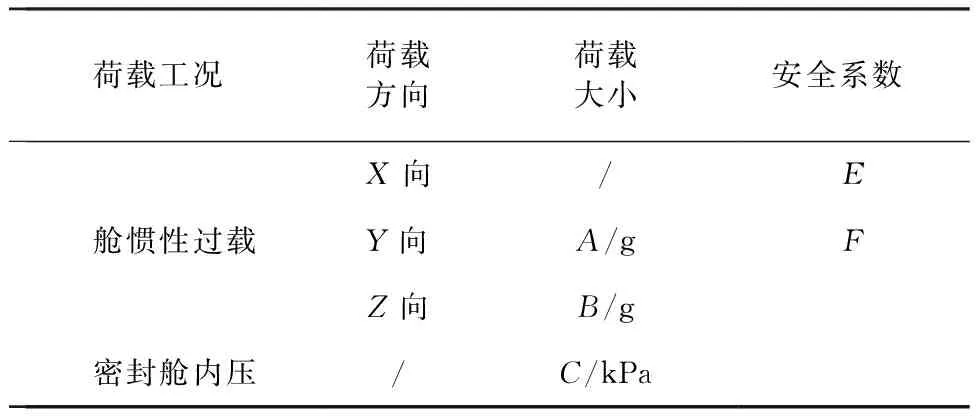
表1 荷载

4 优化

4.1 设计变量

设计变量包含蒙皮厚度和肋条截面尺寸两部分。蒙皮分为上蒙皮和下蒙皮，肋条截面形状为帽形，共2种截面形状，如图6、7所示。除图中45 mm、90°为定尺寸，其余标注尺寸均为肋条截面设计变量。

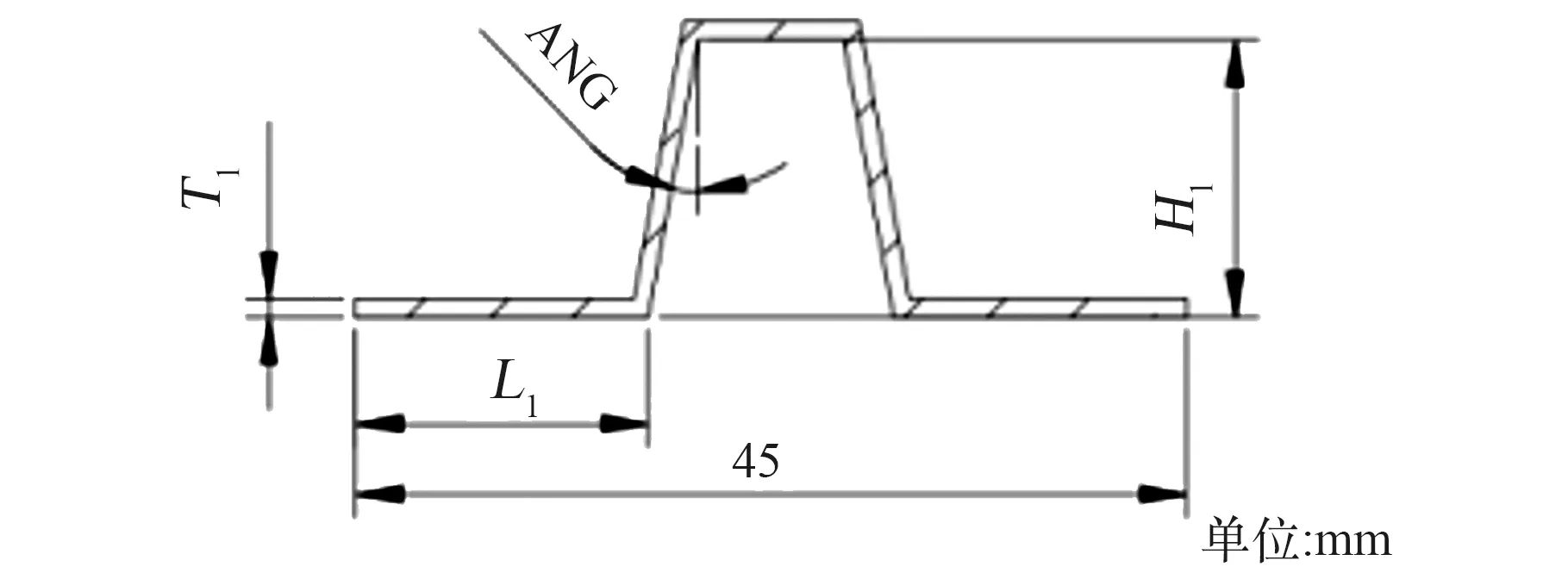
图6 帽形截面1Fig.6 Hat cross section 1

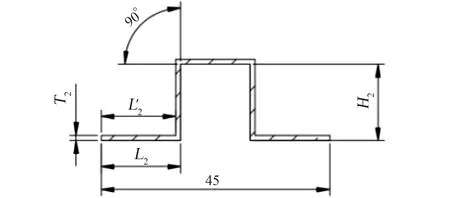
图7 帽形截面2Fig.7 Hat cross section 2

对肋条提出4种分组方案，以设置不同数量的设计变量，具体分组情况如下：

1)仅按截面形状分组(方案一)。X2、X4肋条安装在密封舱外侧，用来安装外部设备，截面为帽形截面2，其余肋条安装在内部，均为帽形截面1。故X2、X4为一组；其余同截面形状肋条为一组,共2组。

2)按截面形状和应力状态分组(方案二)。在方案一的基础上，将X2、X4分为一组，其余为帽形截面1的肋条因数量较多，将按应力状态进行分组。X5为地板框，安放设备1，Y1、Y2靠近侧舱门，三者应力均大于100 MPa，故分为一组；其余肋条应力小于100 MPa为一组。故：X2、X4为一组；X5、Y1、Y2为一组；Y3、Y4、……、Y10、X1、X3为一组。共3组。

3)按截面形状和应力状态分组(方案三)。在方案二的基础上，对于Y3、Y4、……、Y10、X1、X3，考虑到横纵肋条所受荷载差别较大，Y3、Y4、……、Y10应力均在80 MPa左右，而X1、X3在30～40 MPa之间。故X2、X4为一组；X5、Y1、Y2为一组；Y3、Y4、……、Y10为一组；X1、X3为一组，共4组。

4)仅按应力状态分组(方案四)。将应力状态接近的分为一组，故X5、Y1、Y2为一组；Y3、Y4、……、Y10为一组；X1、X3为一组；X2为一组；X4为一组，共5组。

利用式(1)计算各方案设计变量数：

X=ω×i+2

(1)

式中：X表示总设计变量个数；ω为组数；i为肋条截面所定义的设计变量数；2为蒙皮的设计变量数。故各方案的设计变量数为：方案一10个；方案二14个；方案三18个；方案四22个。

4.2 优化数学模型

优化设计的数学模型是描述实际优化问题的实际内容、变量关系、有关实际条件和意图的数学表达式，是进行优化设计的基础[6]。密封舱优化数学模型为式(2)：

(2)

采用零阶算法将各方案依次进行优化，设置优化迭代次数为50次，并设置算法的允差[7]为0.25。

4.3 优化结果及验证

将上述各方案优化后的设计变量重新带入到ANSYS模型中进行验证，各方案mises应力云图如图8所示，均满足强度要求。各方案的荷载屈曲系数λ分别为-0.36、-0.35、-0.36及-0.36，表明结构不会失稳，均满足约束条件。各方案目标函数迭代曲线如图9所示，各方案优化结果列表如表2所示，其中“Δ”为优化结果相对原始质量的变化，负值表示减少。

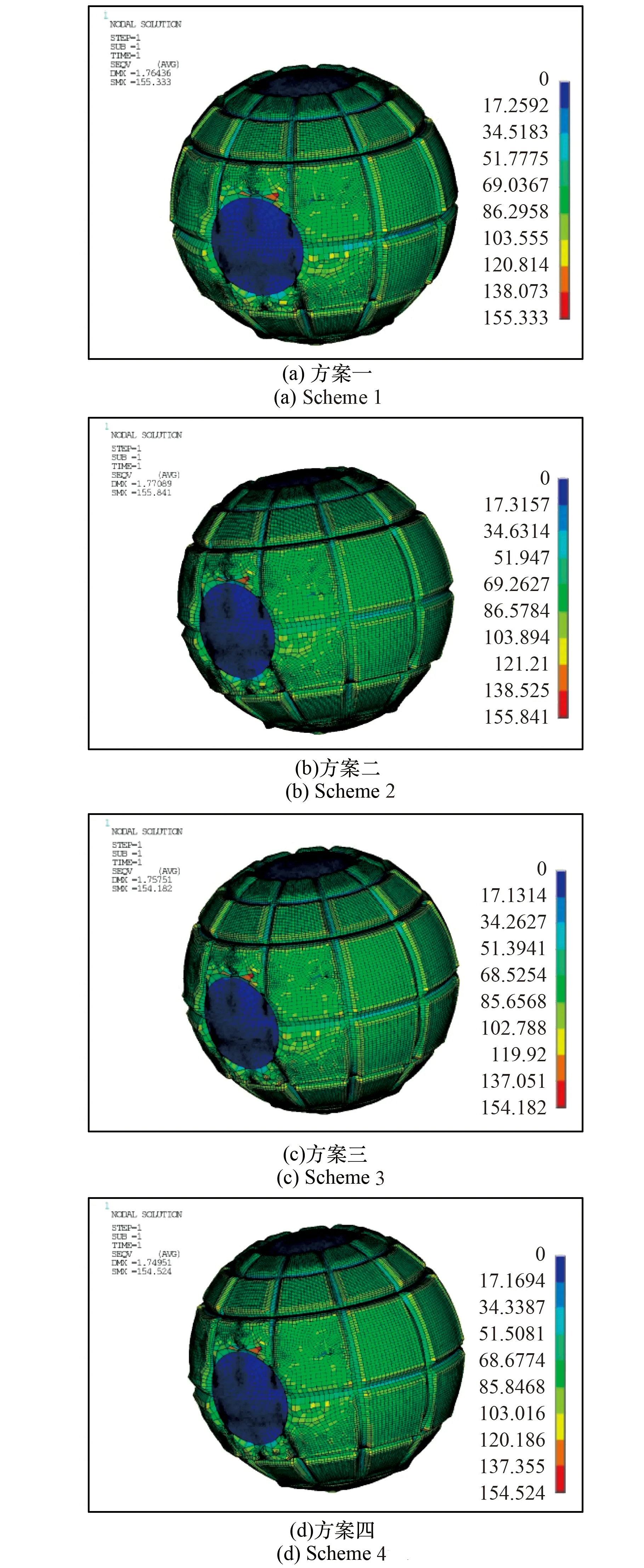
图8 Mises应力云图Fig.8 Cloud picture of Von Mises

图9 目标函数迭代曲线Fig.9 Iteration curve of objective function

表2 优化结果

5 结果分析

由图9、表2可知，从方案一到方案四，随着组数增加，设计变量不断增加，优化曲线越来越不容易收敛，优化结果质量呈现先下降后上升的趋势。

从方案一到方案二，优化效果上升是因为随着设计变量的增加，设计空间更加广阔，能够单独进行优化的肋条数量增加，增大了搜寻到最优解的可能性。

从方案三到方案四，优化结果质量上升是因为方案三、方案四对肋条的分组过细，致使设计变量数量过多，使得①搜索次数呈指数级上升，导致算法无法有效探测巨大的搜索空间；②随着问题维度的升高，问题的局部最优解的数目增多，导致算法容易陷入局部最优解，从而难以找到全局最优解，所以优化效果不升反降。

6 结论

1)通过对肋条进行适当的分组，增加设计变量个数能最大程度上降低目标函数质量，获得更优的设计方案。

2)若不分组，设计变量过少，优化效果不明显。相反，若分组过多，导致设计变量过多，也不能取得理想的优化结果。只有适当的将肋条进行分组，将设计变量数量控制在合适的范围之内，才能充分降低目标函数。

3)在4种方案中，方案二的优化后质量最低，为62.994 kg，比原始设计质量减少了10.7%，可为实际工程中结构参数的选取提供参考。