润物细无声

朱群

一、案例背景

众所周知，函数是高中数学的重要概念之一，函数的思想和方法贯穿了整个高中数学教学，教学要求用集合与对应的语言刻画函数概念，教学要通过对函数概念的理解，让学生达到从直观感知到抽象思维的发展，难度较高。

二、案例描述

师：（大家好！）这节课我们要学习函数，初中已经学过函数，大家能不能举例几个例子说明什么是函数？

生1：买作业本，需要付的钱随作业本的数量变化而变化，付的钱是作业本的函数。

生2：早上上学离开家的距离和时间成正比例函数。

生3：y = 2x+1

师：不错，刚刚大家已经举了一些函数的例子，那我们来看看课本上的例子（多媒体展示）。

（课本例题）：一枚炮弹发射后，经过26s落到地面击中目标.炮弹的射高为845m，且炮弹距地面的高度h（单位：m）随时间t（单位：s）变化的规律是h=130t-5t2炮弹距地面高度h是时间t的函数吗？为什么？

几何画板演示：函数图像上的动点P标出横、纵坐标，拖动点P，显示时间和高度，直观反映炮弹距离地面的高度随时间t的变化情况。

（学生的眼神亮了）

生：（众答）炮弹距地面的高度h是时间t的函数。

师：炮弹的高度h随飞行时间t的变化而变化，所以炮弹距地面高度h是飞行时间t的函数。飞行时间t的变化范围是数集A={t|0≤t≤26}，炮弹距地面的高度h的变化范围是数集B={h|0≤h≤845}，数集A中的任意一个时间t，在数集B中都有唯一的高度h和它对应。

师：现在老师给出3个问题（PPT展示）。

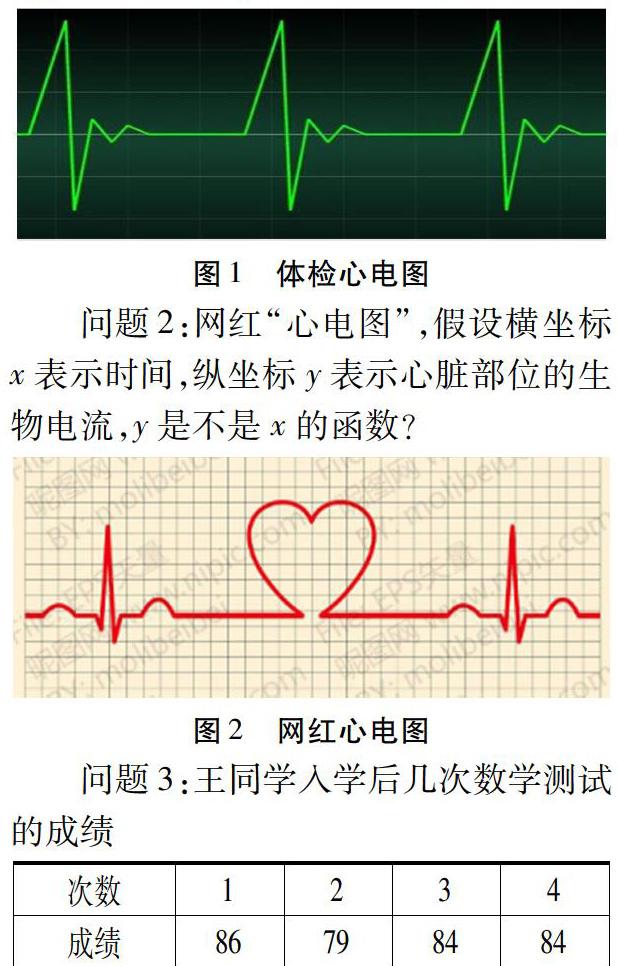
问题1：体检时的心电图，图上点的横坐标x表示时间，纵坐标y表示心脏部位的生物电流，y是不是x的函数？

激励讨论后，各组代表陈述观点：

组1代表：1是函数，2也是函数，因为可以用图象表示。

组2代表：1是函数，2不是函数，感觉有诈，但说不出来。

组3代表：同意一组观点。

组4代表：1是函数，2不是函数，函数中y随x的变化而变化，（上讲台指图）可是这一段中，x逐渐增大的时候，y不知道咋个取值。

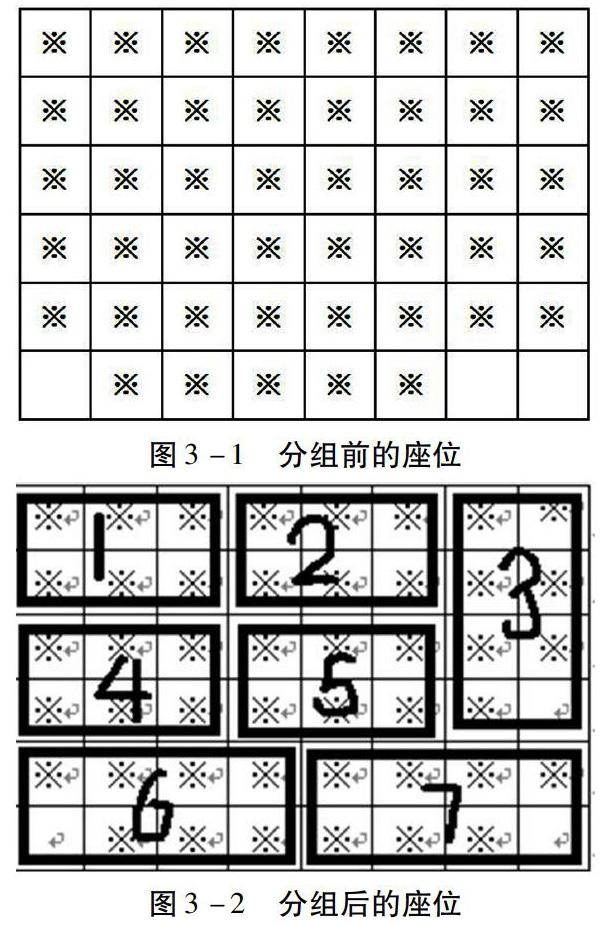
组5代表：网红心电图不是函数，心形部分y的变化有增加，有减小，不知道该算哪一段（指图发言）。考试成绩是考试次数的函数，成绩随次数变化而变化。V组6代表：网红心电图不是函数，成绩也不是，因为没有解析式，也没有图像。

组7代表：同意六组结论。

师：各组都发表了自己的意见，到底是不是函数拿什么作为依据？这几个题拿初中的定义来判断似乎有点为难，那怎么办？

生：（众答）看书。（笑）

（学生阅读）

一般地，我们有：设A、B是非空的数集，如果按照某种确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f（x）和它对应，那么就称f：A→B为从集合A到集合B的一个函数（function），记作：y=f（x）

其中，x叫作自变量，x的取值范围A叫作函数的定义域（domain），与X的值相对应Y值叫作函数值，函数值的集合叫作函数的值域。

师：拿题目1对比，A相当于什么？

生4：（指图）这一段时间，测心电图的这段时间。

师：B相当于什么？

生5：（指图）这部分生物电流职。

师：对应关系f是什么？

生：（犹豫）……

师：不太确定？这个对应关系能不能理解为这是图像的对应关系？

生6：可以。但写不出解析式。

师：一定要有解析式吗？课本定义如何描述？

生7：确定的对应关系。喔，所以不一定要有解析式。

师：集合A中的任意一个时间x，能否在B中都有唯一的值和它对应？

生8：能。

师：所以结论是？

生：（众答）是函数。

师：题目1中，任意一个时间，都能找到唯一的y值，生物电流和它对应，y是x的函数。

师：现在根据定义，请一组纠错问题2。

组1代表：题目2中，心形位置，一个时间，有几个y值和它对应，y不是x的函数。

师：请六组纠错问题3。

组6代表：一次考试对应一个成绩，是函数。

师：非常好，如果例3中，在第三次考试的时候，王同学生病请假了，没有成绩，请问，王同学的数学成绩是不是考试次数的函数？

生9：不是函数，第三次考试没有对应的。

师：非常好，A中的元素3没有和它对应的值，我们再来解读概念中的关键词？

生10：两个非空的数集A、B，对应关系f，任意一个数，唯一确定的数和它对应。

概念探究结束。

三、案例分析

“以学为主”的课堂教学绝非“学为中心”，也非“教为中心”，而是教与学的有效结合，教学强调学生的主体性，通过学生探索、学习获得新知，形成学科思维。教师在课堂教学中充当的角色是引导者，设置合理有效的问题，是课堂教学有效性的保障。

1.问题情境创新化，激发学生学习兴趣

高中数学课的通病是课堂气氛不活跃，学生不愿意回答问题，其深层次的原因是老师在问题设置中没有创新，学生兴趣没有被激发，难以融入课堂。创新型问题情境，能引发学生的认知和对课堂浓厚的兴趣，激发学生思维，增强学生学习的内动力，从而达到以学为主的目的。

2.问题设置基础性，注重探究问题本质

《高中数学课程标准》（2017版）中指出：数学学科核心素养是数学课程目标的集中体现，是在数学学习和应用的过程中逐步形成和发展的。数学学科核心素养包含：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析。数学抽象是指通过对数量关系与空间形式的抽象，得到数学研究对象的素养。主要包括：从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系，从事物的具体背景中抽象出一般规律和结构，并用数学语言予以表征。高中数学课程标准强调教学活动是学科素养培养的主要途径。对大部分学生而言，高中数学概念比较抽象，自主学习往往不知所措，找不到研究问题的入手点，也难深究其本质，没有形成良好的数学思维，因而达不到高中数学核心素养要求，因此，概念教学中要注重体现基本概念的形成过程，从学生认知出发，设置基础性问题，引导学生探究概念的本质，使学生经历从具体实例中抽象出数学概念，促使学生准确理解和掌握概念，提高从数学角度发现和提出问题的能力、分析和解决问题的能力。

3.问题设置层次化，引导学生探究新知

高中数学课程标准中强调返璞归真，努力揭示数学概念、法则、结论的发展过程和本质。数学课堂要讲逻辑推理，更要讲道理，通过典型例子的分析和学生自主探索活动，使学生理解数学概念、结论逐渐形成的过程，体会蕴含在其中的思想方法，把数学的学术形态转化为学生易于接受的教育形态。高中数学概念教学中，问题设置层次化的目的在于引导学生由浅入深，一步一步发现问题的本质，构建良好的数学思维模式。问题之间要合理的衔接，要有启发性，要照顾到不同层次的学生，让所有学生都“有事做”，能思考，积极参与到课堂教学中。

学习的有效性依赖于学生愿不愿学，当学生能自觉参与和思考，学习的有效性自然就提高了。“以学为主”的课堂模式中，合理、有效地预设问题，为学生探究问题明确方向，让学生在探究中体验成功的快乐，并逐渐构建学科知识体系。

（作者单位：云南省昆明市第三十中學）