基于学情活用教材，打造高效课堂

李亚平

【摘要】教材是教师教和学生学的主要依据，教师在教学过程中要基于教材，又不能拘于教材。教师应从学生实际情况出发，基于学情活用教材，拓宽课堂教学空间，真正提高课堂教学的实效，从而更好地促进学生的发展。

【关键词】平行四边形面积；教材；学情

中图分类号：G623.5文献标识码：A文章编号：0493-2099（2020）33-0096-02

Use Teaching Materials Basedon Academic Conditionsto Create Efficient Classroomss

——Take the Teaching of "Area of Parallelogram" of PEP Edition as an Example

（Primary SchoolAffiliated to Huaibei Normal University，China） LIYaping

【Abstract】Textbooks are the main basis for teachers to teach and students to learn. Teachers should base their teaching on textbooks and not be limited to textbooks. Teachers should start from the actual situation of students， use teaching materials based on their academic conditions， broaden the classroom teaching space， and truly improve the effectiveness of classroom teaching， so as to better promote the development of students.

【Keywords】Parallelogram area； Textbook；Academic situation

在学校举办的同课异构活动中，三位年轻的教师都执教了《平行四边形的面积》。三位教师中有两位教师秉承教材的设计进行教学，另一位教师则另辟蹊径。两种教学思路最大的不同是：第一种教学借助了方格图，从“正面强化”入手，先感知，再动手验证，推导出面积公式；第二种教学弃用教材中的方格图，直接让学生求平行四边形的面积，先猜想“试误”，再引导学生割补转化。这两种教学思路哪一种更符合学生的学情？怎样融合两种教学思路的优点？怎样的教学能引发学生的深度学习？笔者在对《平行四边形的面积》这一教学内容，不同时间、不同版本的教材进行对比研究的基础上，选取了四年级的50名学生（这些学生已经学习了“平行四边形的认识”），试图通过学情前测了解学生的真实想法，寻找学生的真问题，找准教学的起点。

一、教材分析

《平行四边的面积》是人教版五年级上册第六单元多边形面积的第一节课，是小学数学重要的教学内容之一，有着承上启下的作用。面积是指“平面或曲面封闭图形所围的区域的大小”，这个大小可以用一个数量来描述。面积计算的基本方法是“单位面积度量法”，长方形的面积就是通过此方法推导出来的。平行四边形的面积计算是以长方形面积计算为基础，以未知转化为已知的基本方法开展学习。教材呈现的推导手段有两种：一种是“单位面积度量法”（数方格），另一种是“割补法”。通过数方格，沟通两个图形之间的联系，为下一步“割补法”探索平行四边形的面积做准备。接下来是借助几何直观，利用出入相补的原理，将平行四边形转化为等底等高的长方形，从而得到平行四边形的面积计算公式。平行四边形的面积也是学习三角形、梯形及组合图形面积的基础，是发展学生的空间观念、培养学生的推理能力、渗透数学思想的载体。

二、学情前测及分析

教师为学生提供空白的平行四边形（底是6厘米，邻边长是4厘米，高是3厘米，但给学生的图形中没有标注底与高的数据），要求学生求出它的面积。

前测发现：有28%的学生作业是空白的或只测量了几个数据，有8%的学生将面积算成了周长，这两部分学生对平行四边形面积的思维水平还停留在前认知阶段。有32%的学生已经认识到平行四边形面积的相关特征，但受到负面迁移的影响，把面积算成了邻边之积。这部分学生能整体辨认图形，但无法用图形的特征来分析图形。有32%的学生正确地算出了图形的面积是18cm2。

笔者对会计算面积的这16名学生又进行了再次测试，请他们用文字、图形来说明为什么要这样求平行四边形的面积。其中的10人表示不太清楚，这部分学生能分析图形的组成要素及特征，利用这种特征解决几何问题，但无法关联性质，只知其然不知其所以然。还有6位学生能利用“割补法”成功将平行四边形转化成长方形，计算出面积。这部分学生的几何思维水平已经到达了非形式化的演绎水平。

三、思考

（一）探讨方格圖能否使用以及怎么用

通过对学情的分析发现，当学生第一次求平行四边形的面积时，大多数的学生是很难想到用“割补”的方式把平行四边形转化为长方形。受之前长方形、正方形面积以及平行四边形“不稳定性”等学习经验的负迁移，学生认为平行四边形与长方形之间可以相互转化的理由是：平行四边形能拉成长方形，因此可以计算拉成的长方形的面积。很显然，学生对与“怎样变”才是“等积”的，这一转化的关键是疑惑的。如何突破这个难点，方格图是很好的铺垫。笔者认为方格图的作用有三点：提供面积可数的直观，暗示形成割补的思路，实现从数到算的转变。那么方格图究竟怎样用呢？笔者认为可以这样进行：

1.引入。出示情境（两个花坛，一个长方形，一个平行四边形），提出问题：两个花坛哪个大？由于长方形的面积学生已经会算了，那如何计算平行四边形的面积呢？切入主题。

2.学生猜想，交流。

3.演示实验。教师拉动活动的长方形的框架，学生观察：什么没变？什么变了？得出结论：平行四边形的面积不能用“底乘邻边”计算。

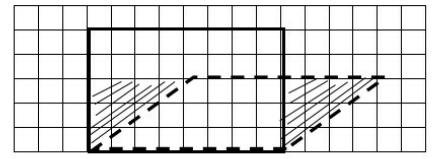
4.深入辨析。把长方形和推拉后的平行四边形放在方格图中。提问：你能数出长方形的面积吗？学生很容易得出结论。

学生经过观察思考后发现，可以把不够一格的合到一起数，或者直接把右边的三角形割补到左边拼成一个新的长方形。通过计算长方形的面积得到平行四边形的面积。接下来是学生的操作验证，探究出平行四边形与转化后的长方形的等量关系，概括出面积公式。有了方格纸为依托，学生后来的探究有了基础，提高了课堂教学效率。

（二）如何凸现转化思想，实践有效建构

在教学中要渗透联系的观点，凸现转化的思想，真正实现意义建构。在本课的教学中，要让学生充分体会转化思想的精髓。转化思想的萌生是源于数平行四边形时出现了“不满一格”的情况；转化的目的在于将“平行四边形的面积”这一新知识转化为已经学过的“长方形的面积”这一旧知识；转化的根据是等积变换。在这里，需要指出的是平行四边形转化为长方形的方法有很多，其本质并没有区别，教师要善于通过变式引发学生思考，通过对比辨析让学生对概念的认识不局限于一个点，而是成为一条线。

（三）教学中需要注意的几个问题

1.不可完全否定平行四边形面积与两条邻边的关系。平行四边形的面积计算公式是底乘相对应的高，但并不是说与邻边没有关系。事实上，平行四边形的面积，可以通过邻边相乘再乘两边夹角的正弦值来计算。2.等底等高的平行四边形形状可以不同，但面积一定相等。面积相等的平行四边形并不一定是等底等高的。3.设计练习题时给出的平行四边形的相关数据要有科学性，不可随意编造。

学生的认知结构和教师教学内容的数学知识结构有时是有区别的，教师要秉承实证精神对学情和教材的编写作出科学分析，以此為基点，围绕跨越障碍，突破难点的核心问题开展教学活动，让数学课堂变得更有深度，更有活力。

参考文献：

[1]靖梅.核心素养视角下小学数学教学过程设计研究——以“平行四边形面积”的教学为例[J].小学教学参考，2020（11）.

（责任编辑袁霜）