融合贝叶斯深度学习的计算机大数据频繁项挖掘算法

刘兴建 原振文

摘要：随着数据每天呈指数级增长，频繁项集挖掘的效率和可伸缩性问题变得更加严重。因此，提出融合贝叶斯深度学习的计算机大数据频繁项挖掘算法（Sequential growth），并在MapReduce框架上实现。为了测试算法的性能，在具有大型数据集的MapReduce框架上进行了不同方面的实验。结果表明，Sequential growth算法具有良好的效率和可扩展性，尤其在处理大数据和长项目集时。

关键词：频繁模式挖掘;频繁项集挖掘;MapReduce;贝叶斯深度学习;可扩展性

中图分类号：TP301文献标志码：A

文章编号：2095-5383（2020）04-0038-05

Frequent Item Mining Algorithm of Computer Big Data

based on Bayesian Deep Learning

LIU Xingjian1， YUAN Zhenwen2

（1.Department of Computer Application Technology， Guangdong Business and Technology University， Zhaoqing 526040， China;2. Artillery Academy， National University of Defense Technology， Changsha 410111， China）

Abstract：

Frequent itemsets mining （FIM） is an important research topic because it is widely used in the real world to find frequent itemsets and mine human behavior patterns. As data grows exponentially every day， the efficiency and scalability issues of frequent itemset mining have become more serious. Therefore， a frequent item mining algorithm （Sequential growth） of computer big data that integrates Bayesian deep learning was porposed in this paper， and it was implemented on the MapReduce framework. In order to test the performance of the algorithm， experiments in different aspects were carried out on the MapReduce framework with large data sets. The results show that the Sequential growth algorithm has good efficiency and scalability， especially when processing large data and long itemsets.

Keywords：

frequent pattern mining; Frequent Itemset Mining（FIM）; MapReduce; Bayesian deep learning; scalability

频繁模式挖掘（frequent pattern mining）是数据挖掘的最重要技术之一，它在各种领域中都有广泛应用，例如市场篮分析、网页点击分析、患者路径分析、DNA序列发现以及最近的无缺陷率改进等[1-4]。频繁项集挖掘（Frequent Itemset Mining，FIM）问题首次出现在1995年，这是基于1994年的工作进行的扩展研究工作，Gupta等[5]介绍了2种基于Apriori的算法，分别称为AprioriAll和AprioriSome，FIM问题逐渐引起了人们的广泛关注，并成为数据挖掘的重要研究课题之一。Apriori算法也成为FIM最重要的概念之一，并以此为基础拓展了许多算法[6-7]。FIM的另一种方法称为Eclat。与Apriori使用自下而上的广度优先搜索策略不同，Eclat使用具有交集的广度优先方法来挖掘频繁项集[8]。 Eclat将事务数据库转换为其垂直格式。 每个项目集与其封面（也称为tid-list）一起存储。垂直数据库D′定义为：D′=ij，Cij=tidij∈X，tid，X∈D，其中Cij是ij的最新列表。在垂直数据库中，项目集Y的支持可以通过与任意2个子集的tid-list相交来计算。它可被表示为supportY=∩tj∈YCij。

基于Apriori的算法以世代扫描方式挖掘频繁项集。将串行Apriori算法应用于MapReduce框架的最便捷方法是MapReduce作业的多次迭代，以生成候选序列并扫描其在数据库中的包含度。但是，MapReduce程序通常会从分布式文件系统（DFS）读取输入数据，并将输出数据写入DFS。基于MapReduce的Apriori FIM算法的开销可能因為MapReduce作业的启动和通信很昂贵。此外，与串行Apriori一样，基于MapReduce的Apriori面临的最关键挑战之一就是昂贵的候选项目集生成和事务数据库扫描。先前的研究表明，基于Apriori的算法在处理庞大的数据集或较长的事务长度时情况更为严峻[9]。为了减少MapReduce迭代，Eclat使用垂直数据库格式为每个项目集构造一个前缀树。它以深度优先的方式遍历前缀树，通过应用任意2个子集的交集来挖掘频繁项集。但这种方式的垂直数据库需要存储在主存储器中，这是处理大规模事务数据库的另一个挑战[10]。

本文提出融合贝叶斯深度学习的计算机大数据频繁项挖掘算法（Sequential growth），算法采用字典顺序的思想来构造候选序列子集，以提高效率，节约成本。另外，Sequential growth以基于支持的广度方法产生频繁的项目集。在每个MapReduce迭代中，不常用的项目集都将被删除。它显著减少了每个MapReduce作业的内存消耗和启动时间。

1 频繁项挖掘算法

1.1 基于MapReduce的Apriori算法

在MapReduce框架上采用串行Apriori算法的最自然的方法是将生成候选项目集和扫描内容的过程转换为map-reduce函数，然后迭代分配作业。以这种方式设计的算法归为k相算法，因为一个长度为k的交易数据库（k是最长的交易长度）最多需要k次迭代才能挖掘出完整的频繁项目集。每个阶段都包含2个MapReduce作业，1个用于生成候选项目集，另1个用于扫描数据库以对它们的出现进行计数。这2个MapReduce作业将继续交替运行，直到没有生成任何候选项集为止[1-4]。由于MapReduce框架不适用于迭代过程，因此开发了基于MapReduce的Apriori算法的服务还原，以通过优化挖掘完整频繁项集所需的MapReduce阶段数来降低启动成本。Lin等[11]提出了2种算法，固定通行证联合计数FPC和动态通行证计数DPC。以n和p为参数，FPC在p个相位后开始生成具有n个不同长度的候选对象，并在一个数据库中对其频率进行计数。DPC算法类似于FPC，不同之处在于n和p根据每个阶段生成的候选数动态确定。

1.2 单相算法

一阶段算法仅需要一项MapReduce作业即可挖掘所有频繁项集。该算法在其map函数中逐行生成所有可能的交易子集（组合），并归纳reduce函数中的全局支持。像这样的方法，候选项目集的增长率与交易的平均长度成指数比例。 例如，在平均长度为k且交易总数为T的情况下，单相需要生成平均C=T×2k-1个候选项目集。生成如此庞大的候选数据集，显然无法满足单相的可伸缩性，有学者提出的一项相关工作称为单次通过计数SPC。SPC与FPC和DPC一起用于分析不同实现对性能的影响。

2 融合贝叶斯深度学习的顺序增长

2.1 字典顺序树

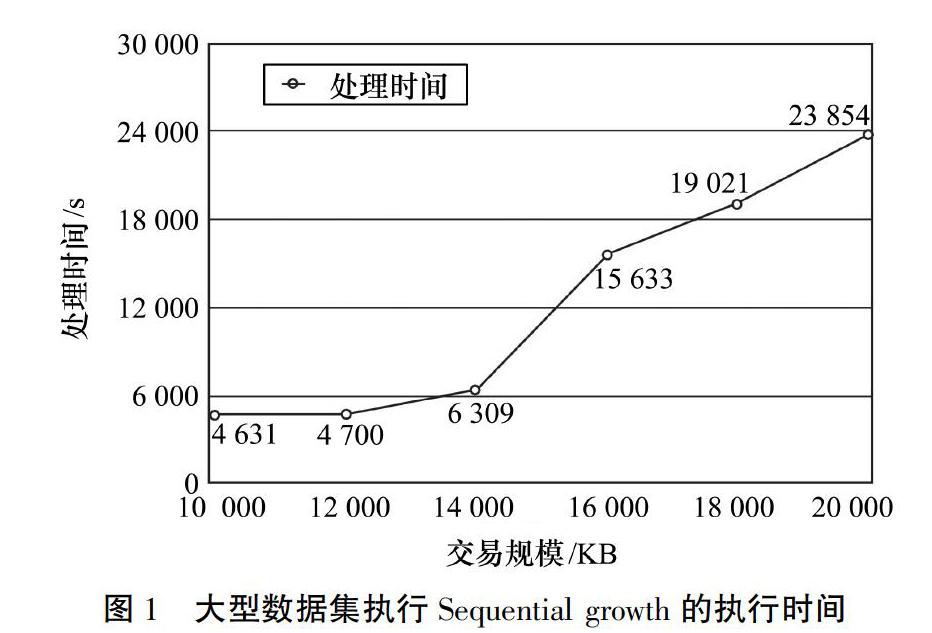
根据已有算法，字典顺序集定义为：设t=j1， j2，…， jk，t′=j′1， j′2，…， j′l。然后t

1）对于某些h，0≤h≤mink，l，对于r

2）k

另外，根据Apriori的定义，序列β=（b1，b2，…，bn）是α=（a1，a2，…，am）的子序列，而α是β的超序列，如果存在整数1≤j1

L=∩n-1l=0plαα∈ql（1）

其中：plα表示pl与α连接。

字典顺序树的功能是构建候选生成空间。字典顺序树中的每个节点表示1个子序列，其高度与该级别上子序列的长度相对应。字典顺序树可以通过以序列增长方式迭代地将每个节点及其后缀串联在一起来扩展。length-（k+1）序列是其父节点（length-k）和父级后缀项的串联。例如，V=（s1，s2，s3）是S的长度3子序列。长度4子集V′={（s1，s2，s3，s4），（s1，s2，s3，s5），（s1，s2，s3，s6），…，（s1，s2，s3，in）}是通过将S中跟在s3之后的每个项目附加到V的末尾而获得的。从长度1开始，到n可以从字典顺序树中检索S的子序列。2020年第4期

刘兴建

，等：

融合贝叶斯深度学习的计算机大数据频繁项挖掘算法

成都工业学院学报http：//paper.cdtu.edu.cn/第23卷

2.2 贝叶斯深度学习

贝叶斯深度学习中的修剪策略也是设计高效FIM算法的重要因素。与单阶段算法在一次迭代中生成交易数据库的所有可能子集的方法不同，Sequential growth以1～k的基数迭代执行以生成候选项目集。将候选项集生成的延迟称为“惰性挖掘”，这是提出的算法的有效修剪策略。将Apriori属性应用于字典顺序树，如果不经常使用某个节点，则可以删除所有子节点。Sequential growth减少了每次迭代的候选项目集的大小，并显着减少了内存消耗。因此，执行可使数据适合主存储器，以防止昂贵的上下文交换过程。 Sequential growth算法是根据字典顺序树的概念和惰性挖掘修剪策略设计的，并在MapReduce框架上实现以实现分布式执行。

2.3 扩展序列增长方法用于轨迹模式挖掘

通常事务中的每个项目都可以分为2个项目集，1个前缀和1个后缀。因此，Sequential growth算法中建立字典顺序树的方法也可以应用于其他关联规则挖掘算法来构造其候选空间。本节提供了一種用于轨迹模式挖掘TPM的示例算法，该算法是Sequential growth的较小微调。由于TPM的研究问题不在本文讨论范围之内，因此本文中的TPM问题得以简化，以易于理解。轨迹记录可以表示为Euclid Math TwoTA@=Euclid Math TwoSA@，Euclid Math TwoAA@，其中Euclid Math TwoSA@=ρ0，ρ1，…，ρn是n+1个移动位置的序列，而Euclid Math TwoAA@=μ1，μ2，…，μn是一组过渡时间，因此μi=Δti=ti-ti-1。轨迹数据库

t=t1，t2，…，tm是一组轨迹。suppDEuclid Math TwoSA@是轨迹数据库

t中Euclid Math TwoSA@的频率。给定最小支持阈值smin和时间公差τ，如果suppDEuclid Math TwoSA@≥smin且每个μi∈Euclid Math TwoAA@的μi≤τ，则

Euclid Math TwoTA@=Euclid Math TwoSA@，Euclid Math TwoAA@频繁，称为T型。TPM是找到所有T-轨迹数据库t中的模式Euclid Math TwoSA@，Euclid Math TwoAA@。采矿程序从发现所有“热点”开始。该步骤类似于在Sequential growth算法中挖掘length-1项集，不同之处在于，如果后缀位置（当前点之后的移动位置）的过渡时间大于时间公差，则不会输出这些位置。算法1包含该步骤的伪代码。在算法1中，通过遍历位置序列以截断那些过渡时间大于时间容限的轨迹（第7至9行）。下一步包括通过反复应用字典顺序树的方法来挖掘所有T模式，以在每个mapreduce作业中将序列长度扩展一个。

算法1：GenHotSpot//生成热点

Input：S：{t|t∈Si，t=<ρ0，…，ρn@μ1，…，μn>};

smin：integer;

τ：integer;

Output：L1：{ρ|ρ∈L1，ρ=};

C1：{c|c∈C1，c=};

Map Task（key，value）

1：for each t in Si do

2： loclist=t.split（“@”）[0].split（“，”）;

3： timelist=t.split（“@”）[1].split（“，”）;

4： for（k=0;k

5：tranTime=0;

6：len=k;

7：while（tranTime+=timelist[len]≤τ）do

8： len++;

9：end while

10：key=loclist[k];

11：if（len≥k）then

12： value=loclist.SubArray（k+1，len）;

13： value+=“@”;

14： value+=timelist.SubArray（k，len-1）;

15：end if

16：Output（key，value）;

17： end for

18：end for

3 實验与分析

实验是在由7台机器组成的完全分布式集群环境中的Hadoop 1.2.1和jdk-7u6上执行的。每个内核包含6个内核，分别为Intel（R）I7-4930 3.4 GHz CPU和64 G RAM。所有机器都在Ubuntu 12.04操作系统上运行。一台机器作为主机和从机，其他机器仅作为从机。实验中使用了由IBM Quest综合数据生成器生成的综合数据集，合成数据集的参数分别是：平均交易长度T，平均最大频繁项集长度I和交易总数D。

首先，使用不同大小的事务数据库来测试Sequential growth算法的可伸缩性。综合事务数据集的大小从50 KB到8 000 KB。对于所有数据集，T=10，I=4，最小支持δ=0.1%。结果表明Sequential growth提供了良好的可伸缩性。斜率（处理时间的Δ/事务大小的Δ）表示增加1 KB事务所需的处理时间。当事务大小从4 000 KB增长到6 000 KB时，处理时间就开始大量增加。即使这样，Sequential growth算法仍具有在合理时间内处理此类大型数据集的能力。为了进一步验证算法处理大数据的能力，使用1 000万到2 000万笔交易的数据集执行Sequential growth，其中T=6，最小支持δ=1%。结果如图1所示，它再次确认了Sequential growth的良好可伸缩性。

除了大量的事务外，广泛的事务长度是FIM处理大数据的另一个挑战。接下来，继续验证Sequential growth可以通过在第2次MapReduce迭代后均匀划分分区并通过其有效的修剪策略来解决此问题，使用2%、4%和8%的最低支持来执行具有不同平均交易时间的Sequential growth。图2显示的结果是，Sequential growth在处理从最短的3 B到最长的107 B处理过程中都是高效且可扩展的。Sequential growth被设计为能够与输入文件平均分区。在MapReduce作业的第2次迭代之后，Sequential growth将1条很长的线分成几条较短的线。因此，输入数据集能够被分区并平均分配给每个映射器。这样可以防止进程等待繁琐的映射程序。该部分的代码在算法2的第21～25行中进行了说明。另一个观察结果是，当平均交易时长从35 s增加到40 s时，用于2%最小支持的处理时间增加了3.4倍。但是，对于最低支持8%。这是因为Sequential growth的“惰性挖掘”修剪策略生效。每

次MapReduce迭代期间使用的最小支持阈值越高，

修剪掉的项目集越多。实验结果证明，基于广度支持的修剪策略是提高序列增长性能的重要因素，尤其是在处理长事务时。

为了进一步评估本文算法，进行了几次实验，以与其他2种基于Apriori的算法MR-Apriori和One-Phase进行比较。首先研究从10 KB到2 000 KB不同大小的事务数据集的3种算法的性能。对于所有数据集，T均为10，最小支持δ为0.1%。结果如图3所示，当数据集的大小>50 KB时，MR-Apriori的执行失败。像串行Apriori一样，MR-Apriori仍需要重复运行1个MapReduce作业以生成候选项目集，而另1个运行以扫描数据库。即使在MapReduce框架上实现算法以进行分布式执行，当数据集的大小变得巨大时，内存使用和计算成本仍然可能非常昂贵。此外，在250 KB之后，单相处理时间显着增加。在事务大小为250 KB时，“单阶段”的执行时间大约是“序列增长”的执行时间的2倍，而在2 000 KB时，它的执行时间要高出3倍以上。基于结果，本文算法在处理比较MR-Apriori和One-Phase的大型数据集时效率更高。

图4显示了使用10 KB合成数据集和不同级别的平均交易长度的三种算法之间的性能比较。即使在相对较短的数据集中处理时，单相的性能更好，但

当事务长度>14时，单相的运行时间会大大增加。原因是映射函数生成的中间数据的大小一阶段算法的数量与交易时间成指数比例。执行无法容纳到主存储器中，因此，当事务长度变长时，单阶段的性能效率低下，甚至不可行。

单相和序列增长算法都挖掘频繁项集，而无需重复扫描整个交易数据库。2种算法之间的关键区别在于，“一阶段”可在单个MapReduce作业中生成事务数据库的所有可能子集。相反，Sequential growth以基于支持的广度方法（惰性挖掘）产生频繁的项集。在以上实验的基础上，进一步比较了Sequential growth和One-Phase算法生成的子集的处理时间和总数。对于“单阶段”，执行时间和子集的大小都显著增长，同时平均交易时间也增加了。当平均交易长度=6时，“单阶段”生成的项目集的总数是“序列增长”生成的总数的2倍。但是，当平均交易时长增加到18时，它大约大了172倍。结果证实了先前的观察，“惰性挖掘”提供了一种有效的Sequential growth修剪策略，尤其是在处理平均交易时长较长的数据集时。

除了MapReduce-Apriori和One-Phase，还比较了分布式FIM算法BigFIM的最新成果。为了建立实验，从BigFIM项目下载源代码并进行相应的构建。首先，尝试比较BigFIM和Sequential growth在不同规模的数据集（从50 KB到4 000 KB）下的执行性能。对于所有数据集，T均为10，最小支持δ为0.1%，2种算法的映射器数量均为42。对于BigFIM，前缀树的深度为3。

图5显示Sequential growth优于BigFIM。请注意，由于BigFIM无法完成生成k-FI的过程，因此即使提出的算法能够处理更大的数据集，结果中显示的最大事务大小仍为6 000 KB。根据观察，BigFIM的较长执行時间主要来自生成k-FI的步骤。 BigFIM改用类似于One-Phase的Apriori算法，以生成k长的前缀项集（在本实验中为3），然后切换到Dist-Eclat算法以继续挖掘阶段。因此，在生成前缀步骤期间，BigFIM会面临相同的单相问题。通过使用真实数据集BMSWebView1（Gazelle）比较两种算法的执行时间以及最低支持水平的变化，进行了第二项实验以测试修剪策略的影响。 BMSWebView1包含来自电子商务的点击流数据的59 601笔交易。序列的平均长度为2.42个项目，标准差为3.22。图6显示了最小支持δ从0.1%到1%的执行时间。以0.1%的最低支持执行，BigFIM比Sequential growth更快。尽管如此，与BigFIM相比，Sequential growth的处理时间从26%减少到47%，最小支持大于0.1%。那是因为贝叶斯深度学习的“惰性挖矿”修剪策略生效。因此，较大的δ值将通过在每次MapReduce迭代期间减少更多的不频繁项集而从Sequential growth的修剪策略中获得更多收益。

4 结论

云计算提供了一种在大数据上挖掘频繁项目集的解决方案。效率和可伸缩性对于设计用于处理此类大型数据集的FIM算法至关重要。但是，当前的分布式FIM算法通常会遇到产生大量中间数据或扫描整个交易数据库以识别频繁项集的问题。本文提出了融合贝叶斯深度学习的计算机大数据频繁项挖掘算法，展示了Sequential growth算法运用字典顺序的思想来构造候选序列子集，而无需

在事务数据库上进行详尽搜索，说明广度的“惰性挖掘”修剪策略可有效消除大量中间数据的生成，因此，算法的执行可以更好地适合主内存。实验结果证明，Sequential growth在挖掘大数据集频繁项集的效率和可伸缩性方面优于现有算法。此外，本文还提供了一个示例算法，以演示可以轻松修改Sequential growth，以使其他关联规则挖掘算法适应MapReduce框架。

参考文献：

[1] 高腾飞，刘勇琰，汤云波. 面向时间序列大数据海量并行贝叶斯因子化分析方法[J]. 计算机研究与发展，2019，56（7）：1567-1577.

[2] 王来兵. 基于贝叶斯与生成式对抗网络的手写字文本识别算法[J]. 黑龙江工业学院学报（综合版），2019（8）：31-35.

[3]姜斌，赵梓良，黄灏. 基于反贝叶斯学习的WDMS光谱自动识别研究[J]. 光谱学与光谱分析，2019，39（6）：12-20.

[4] 来纯晓，武振国，金松林. 基于BP神经网络的小麦抗寒性模型构建[J]. 河南科技学院学报（自然科学版），2019（3）：43-49.

[5]GUPTA R K，AGRAWAL D P. Improving the performance of association rule mining algorithms by filtering insignificantTransactions Dynamically [J]. Asian Journal of Information Management，1994，3（1）：7-17.

[6]ARYABARZAN N， MINAEI-BIDGOLI B， TESHNEHLAB M. negFIN： an efficient algorithm for fast mining frequent itemsets[J]. Expert Systems with Applications，2018，105（6）：11-22.

[7] WU S，WANG M，ZOU Y. Research on internet information mining based on agent algorithm[J]. Future Generation Computer Systems，2018，86（3）：56-62.

[8] NJAH H，JAMOUSSI S，MAHDI W. Deep bayesian network architecture for big data mining[J]. Concurrency and Computation： Practice and Experience，2019（1）：4418-4423.

[9] ALJOBOURI H K，JABER H A，KOAK O M，et al. Clustering fMRI data with a robust unsupervised learning algorithm for neuroscience data mining[J]. Journal of Neuroence Methods，2018，299（8）：421-432.

[10] WANG T，ZHANG D，ZHOU X，et al. Mining personal frequent routes via road corner detection[J]. IEEE Transactions on Systems Man & Cybernetics Systems，2017，46（4）：445-458.

[11] LIN T，BORZABADI-FARAHANI A，LANE C J，et al. Apriori feasibility testing of randomized clinical trial design in patients with cleft deformities and class Ⅲ malocclusion[J]. International Journal of Pediatric Otorhinolaryngology，2014，78（5）：725-730.