考虑架悬电机和车体柔性的高速列车振动分析

郭金莹 王静 喻山峰 邬忠萍

摘要：考虑柔性车体和架悬电机，建立高速动车组动力学模型，推导系统传递函数，分析电机悬挂参数对车体、构架和自身振动的影响。仿真结果表明，除采用极小的悬挂刚度外，架悬电机的刚度和阻尼对车体舒适度的影响极小，故在进行车辆系统动力学性能评价时，可以忽略架悬电机的影响。电机悬挂刚度和阻尼对构架的振动略有影响，由于空间位置的限制和电机自身携带振动源，工程上电机悬挂刚度和阻尼一般都较大，因此其对构架振动影响有限。电机悬挂刚度和阻尼对其自身的振动影响相对显著，随着刚度和阻尼的增大，电机的振动加速度RMS均显著降低，然而当刚度增大到2 MN/m以上后其影响减弱。

关键词：动车组;架悬电机;柔性车体;耦合振动;悬挂参数;舒适度

中图分类号：U270.11文献标志码：A

文章编号：2095-5383（2020）04-0017-06

Vibration Analysis of High-speed Trains Considering Suspension

Motor andCarbody Flexibility

GUO Jinying， WANG Jing， YU Shanfeng， WU Zhongping

（School of Automobile and Transportation，Chengdu Technological University， Chengdu 611730，China）

Abstract： Considering the flexible car body and suspension motor， the dynamics model of high-speed EMU was established，the system transfer function was derived， and the influence of the motor suspension parameters on the car body， frame and its own vibration was analyzed. The simulation results show that， in addition to the extremely small suspension stiffness， the stiffness and damping of the suspension motor have little effect on the comfort of the car body. Therefore， when evaluating the dynamic performance of the vehicle system， the influence of the suspension motor can be neglected. The suspension stiffness and damping of the motor have a slight influence on the vibration of the frame. Due to the limitation of space and the vibration source carried by the motor itself， the suspension stiffness and damping of the motor are generally large， so itsr influence on the vibration of the frame is limited. The influence of suspension stiffness and damping on the vibration of the motor is relatively significant. With the increase of stiffness and damping， the RMS of vibration acceleration of the motor decreases significantly. However， its influence decreases when the stiffness gets up to 2 MN/m and higher.

Keywords：EMU; frame-mounted traction motor; flexibility; coupled vibration; suspension; ride comfort

现代铁道车辆车体常采用轻量化设计，尤其是高速列车，然而这将导致其结构刚度损失和车体弹性模态频率降低，其最低阶模态甚至低于10 Hz[1]。随着列车运营速度的提高，轨道激励的频率也随之提高，车体的低阶弹性模态被激发，导致局部路段出现显著的车体结构弹性振动，降低乘坐舒适性。因此，在分析平稳性指标和舒适度指标时，有必要考虑车体结构模态[2-3]。

减轻簧下质量，降低轮轨间的动作用力是高速动车转向架重要的设计原则，我国高速动车转向架普遍采用了架悬方式。电机弹性悬架装置的使用能够提高车辆的稳定性，改善平稳性，降低轮轴横向力[4]。在对车辆系统进行动力学分析时，一般将其等效为构架上的集中质量，忽略其振动，不考虑其悬挂参数对整车性能的影响。黄彩虹等[5]、姚远等[6]建立了考虑电机的横向动力学模型，分析电机悬挂参数和质量参数对稳定性的影响。但对整车动力学性能的影响研究较少。本文

建立包含弹性车体和电机的车辆系统刚柔耦合动力学模型，分析其振动特性及电机悬挂参数对整车動力学性能的影响。

1 车体与电机耦合系统动力学模型

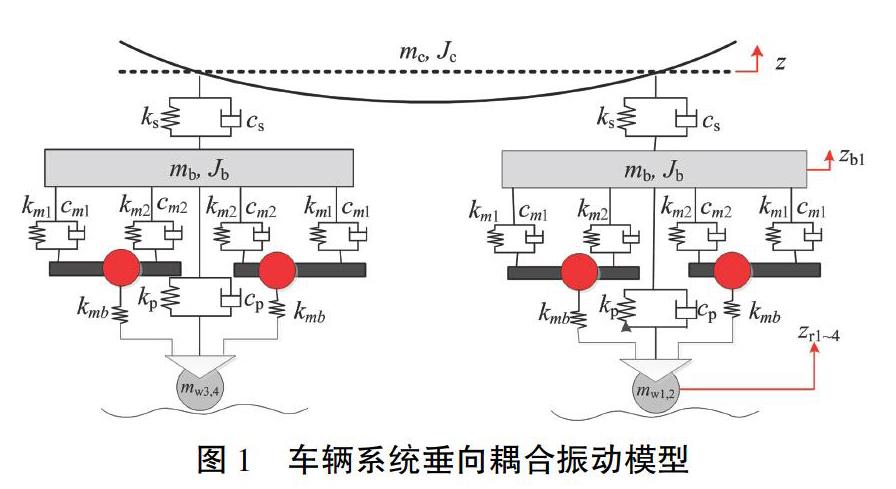
本文以垂向振动为例，介绍考虑车体弹性和设备振动的车辆刚柔系统动力学模型，如图1所示，包括车体、构架和车下设备系统等，以及转向架一系、二系悬挂。

各部件坐标系原点位于质心，以速度v沿轨道中心线x方向运动，坐标系z轴垂直向上。将模型中各个体的坐标系选定在质心处，可以减少惯性力耦合项，使运动微分方程书写更加简洁[7]。模型中仅车下设备的质心与几何中心不重合，考虑设备偏心情况。首先推导悬挂力表达式，进而得到各部件的运动微分方程。系统自由度包括：车体浮沉zc和点头θc、前后构架浮沉zbi（i=1，2）和点头θbi（i=1，2），设备浮沉zmk和点头θmk（k=1～4），以及车体m阶柔性模态，系统总自由度为14+m。

1.1 悬挂力推导

假定轨道刚性无穷大，认为轮对运动与轨道激励完全相同，并假设4条轮对简谐激励分别为：

zr1=z0ejωtzr2=z0ejωt-τ1zr3=z0ejωt-τ2zr4=z0ejωt-τ3（1）

其中：τ1=2Lb/v，τ2=2Ls/v，τ3=τ1+τ2。

一系悬挂力：

Fpi， j=-cpz·bj+（-1）iθ·bj-z·ri-kp（zbj+（-1）iLbθbj-

zri）（2）

二系悬挂力表达式为，

Fsi=-cswcxi，tt-z·bi-kswcxi，t-zbi（3）

其中：i=1，2表示前后构架;wc表示车体垂向运动位移，包含车体的刚性运动和柔性变形，是位置和时间的非线性函数。

电机与构架悬挂力表达式为：

Fbi，mj，1=-cm1[z·biLtθ·bi-z·mj±L1θ·mj]-km1[zbiLtθbi-zmj±L1θmj]Fbi，mj，2=-cm2[z·bi（Lt-L1-L2）θ·bi-z·mjL2θ·mj]-

km2[zbi（Lt-L1-L2）θbi-zmjL2θmj]（4）

其中：i=1，2表示前后构架; j=1～4表示4个电机。

电机与轮对作用力表达式为：

Fmj，rk=-kmb[zmj-zrk]（5）

其中： j=1～4表示4个电机;k=1～4表示4个轮对。

1.2 运动微分方程

车体简化处理为均直欧拉伯努利梁，车体垂向位移为wc（x，t），x为纵向位置，t为时间变量;二系悬挂力为Fs1和Fs2。

其一阶弯曲模态的振型函数为：

Yx=ch βx+cos βx-ch-cossh-sinsh βx+sin βx（6）

其中：和β满足条件1-chcos=0和β=/Lc，

≈（2+1）/2表示弯曲模态阶数。

因此，车体任意位置的刚体位移和柔性变形量的总和表示为：

wc（x，t）=zc（t）+x-Lc/2θc（t）+∑mi=1Yi（x）qi（t）（7）

采用模态叠加法并考虑振型函数的正交性和狄拉克函数特点，可得到车体的3个二阶常微分运动方程：

mcz¨c=∑2j=1FsjIcθ¨c=∑2j=1Fsjxj-Lc/2q¨i+2ξiωiq·i+ω2iqi=∑2j=1Yi（xj）mcFsj（8）

其中：EIβ4iρA=ω2i，μIβ4iρA=2ξiωi。

前、后构架的浮沉运动方程为：

mbz¨b1=Fp1+Fp2-Fs1+Fb1，m1，1+Fb1，m1，2+Fb1，m2，1+F2b1，m2，2Ibθ¨b1=Fp1Lb-Fp2Lb+Fb1，m1，1Lt-Fb1，m2，1Lt+Fb1，m1，2（Lt-L1-L2）-Fb1，m2，2（Lt-L1-L2）mbz¨b2=Fp3+Fp4-Fs2+Fb2，m3，1+Fb2，m3，2+Fb2，m4，1+F2b2，m4，2Ibθ¨b2=Fp3Lb-Fp4Lb+Fb2，m3，1Lt-Fb2，m4，1Lt+Fb2，m3，2（Lt-L1-L2）-Fb2，m4，2（Lt-L1-L2）（9）

同理，电机的浮沉位移和点头位移为：

mmz¨mj=Fmj，rk-Fbi，mj，1-Fbi，mj，2Jmθ¨mj=±（Fbi，mj，1L1-Fbi，mj，2L2）  j=1，3取+; j=2，4取-（10）

综上，系统运动微分方程组包括式（8）～（10），写成矩阵形式为：

M p¨+C p·+Kp=Crz·r+Krzr（11）

p=[zc，θc，q1，…，qn，zb1，θb1，zb2，θb2，zm1，θm2，…，zm4，θm4]T为系统自由度，zr=[zr1，zr2，zr3，zr4]T为轨道激励，M、C和K分别为系统质量、阻尼和剛度系数矩阵，Cr和Kr分别为轨道激励的阻尼和刚度系数矩阵。

1.3 传递函数

对微分方程组（11）进行拉氏变换：

Ms2+CsP+KPs=Crs+KrZrs（12）

将输出Ps与输入Zrs相比得到系统的传递函数，再并将s替换为

jω得到系统的频响函数：

Hω=jωCr+Kr-ω2M+jωC+K（13）

系统频响函数是一个14+m×4阶矩阵，行对应车辆某个自由度的响应，列对应某条轮对激励的响应。例如，第一行为车体浮沉对应4条轮对激励的响应，代数和为该自由度的总响应。基于Matlab编程求解系统运动微分方程。

2 车体和设备耦合振动特征分析

2.1 轨道激励

以德国高低不平顺激励轨道谱为例[7]，

其中：Ω表示波长;Ωc=0.824 6 rad/m;Ωr=0.020 6 rad/m;A为与轨道质量相关的系数，对于低干扰谱A=4.032×10-7 rad·m。已知激励频率可表示为ω=V Ω，V表示车速，则轨道高低不平顺的功率谱密度函数的一般形式为Gω=Sω/V/V，进而转换成：

Gω=AΩ2cV3ω2+V2Ω2rω2+V2Ω2c（15）

2.2 舒适度计算

由公式（13）和（15）可得，车体垂向振动加速度的功率谱密度函数为：

Gacx，ω=GωH-acx，ω2（16）

其中：H-acx，ω为车体在位置x的加速度频响函数，其表达式为：

H-acx，ω=ω2H-zcω+x-Lc/2H-θcω+∑mi=1YixH-qiω（17）

其中：H-zc、H-θc和H-qi分别为浮沉zc、点头θc和弯曲模态qi的位移频响函数，分别对应公式（13）的前3行响应。

指定位置参数x，可以根据式（17）获得车体不同测点处的加速度频响函数。车体中心处的加速度频响函数为：

H-acmx，ω=ω2H-zcω+∑ni=1YixH-qiω（18）

车体在前、后构架上方位置的加速度频响为：

H-acb1，2x，ω=ω2H-zcω±LsH-θcω+∑mi=1YixH-qiω（19）

车体垂向的舒适度指标计算公式为[8]：

NMV=6aWab95（20）

其中：a为指定测点处的垂向加速度均方根值，下脚标表示95%分位数，Wab=Wa·Wb表示垂向加速度的频域加权函数[9]，

Has=s22f22s2+2f1Q1s+2f12s2+2f2Q1s+2f22Hbs=2Kf42f62s+2f3s2+2f5Q3s+2f52f32f52s2+2f4Q2s+2f42s2+2f6Q4s+2f62（21）

其中： f1=0.4 Hz; f2=100 Hz; f3= f4=16 Hz; f5=2.5 Hz; f6=4 Hz;Q1=0.71;Q2=0.63;Q3=Q4=0.8;K=0.4;s=jω。

车体任意点处的加速度均方根值可通过功率谱密度函数计算：

a=1∞0Gacx，ωdω（22）

联合式（16）和（18）可得舒适度表达式：

NMVx=6Φ-10.951∞0Gacx，ωHabω2dω

（23）

其中：Φ-10.95=1.654表示标准正态分布的95%概率密度的分位数;加权滤波器的传递函数

Habω=

HaωHbω，如图2所示。从图2可以看出，在1～40 Hz范围内加速度的加权系数最大。

已知车体上任意测点的加速度频响函数（18）和（19），可以根据舒适度计算公式（23）仿真计算不同工况下的舒适度指标。

2.3 构架和电机振动

构架垂向振动加速度的功率谱密度函数为：

Gab=GωH-zb2（24）

其中：H-zb为构架浮沉加速度频响函数，可利用公式（13）得到，对于前转向架，为第4行，对于后转向架为第6行。

构架点头加速度的功率谱密度函数为：

Gab=GωH-θb2（25）

其中：H-θb为构架点头加速度频响函数，可利用公式（13）得到，对于前转向架，为第5行，对于后转向架为第7行。

电机垂向振动加速度的功率谱密度函数为：

Gam=GωH-zm2（26）

其中：H-zm为电机浮沉加速度频响函数，可利用公式（13）得到，分别对应第8、10、12、14行。

电机点头加速度的功率谱密度函数为：

Gab=GωH-θm2（27）

其中：H-θm为电机点头加速度频响函数，可利用公式（13）得到，分别对应第9、11、13、15行。

3 仿真结果

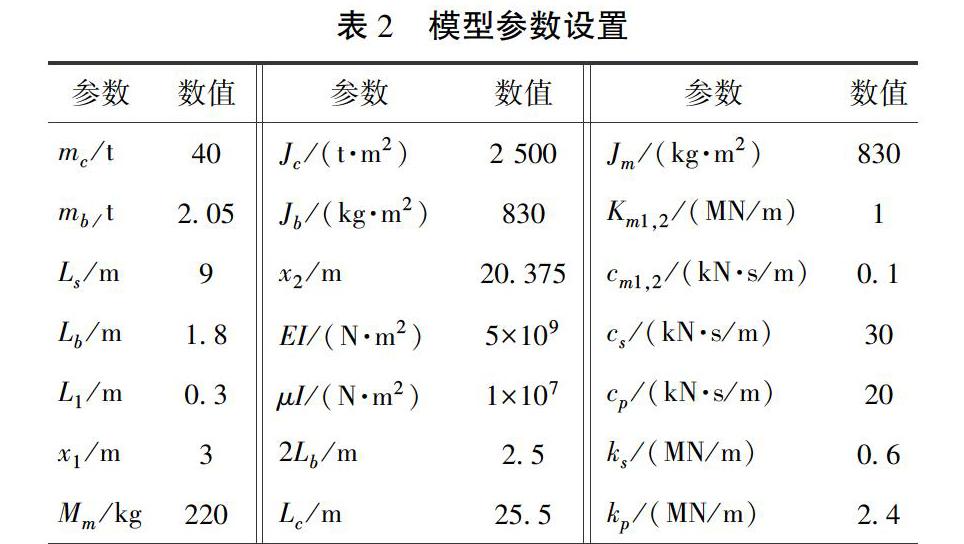
3.1 模型参数设置

参考某时速300 km/h动车组设置模型基本参数，如表2所示。

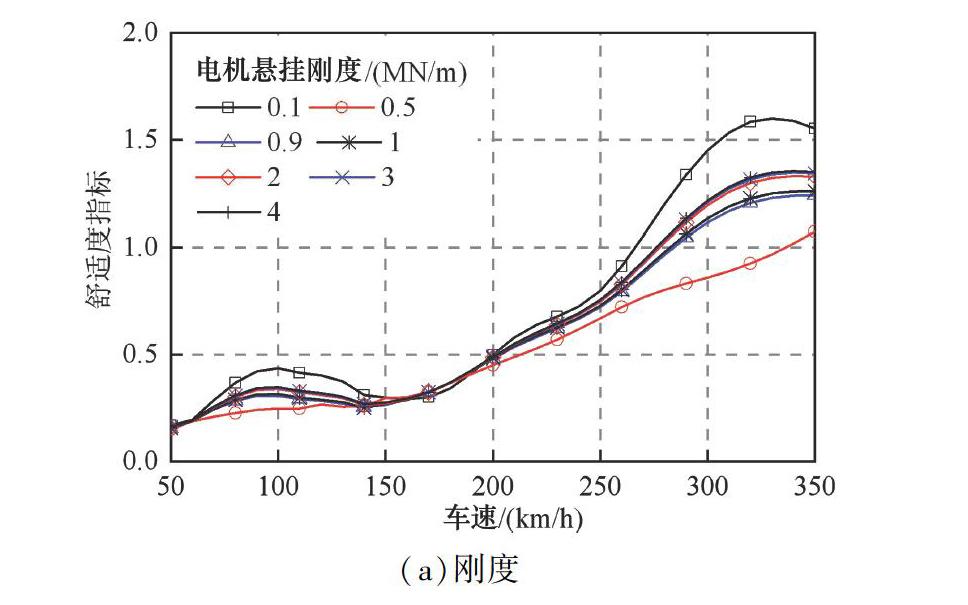
3.2 电机悬挂参数对车体振动的影响

计算不同电机悬挂参数下的车体舒适度指标，见图3。从图3（a）可知，当电机悬挂刚度从0.1MN/m增大到0.5 MN/m时，舒适度指标有所降低，当刚度继续增大后，舒适度指标又增大。然而，电机一般采用较大的悬挂刚度，在1～4MN/m范围内变化时其对车体舒适性影响有限。从 （b）可知，电机悬挂阻尼在100～7 000 N·s/m范围内变化时，对舒适度指标无影响。

3.3 电机悬挂参数对转向架振动的影响

计算不同电机悬挂参数下转向架的振动加速度均方根（RMS），见图4、图5。可知，电机悬挂刚度和阻尼对构架的浮沉略有影響，对构架的点头运动有一定影响，但是构架的运动以浮沉为主，故其影响不显著。当电机悬挂刚度取0.1 MN/m时构架的浮沉运动显著大于其他工况。

3.4 电机悬挂参数对电机振动的影响

计算不同电机悬挂参数下转向架的振动加速度均方根（RMS），见图6、图7。可知，电机悬挂刚度和阻尼对电机的浮沉和摇头都有显著影响。1）当电机的悬挂刚度取值在0.1～0.9 MN/m范围内变化时，随着刚度的增大，电机的点头和浮沉的加速度RMS均显著降低;2）当刚度增大到2 MN/m以上后，其对电机的摇头和浮沉的影响极其有限;3）在各个速度等级上，随着电机悬挂阻尼的增大，电机的浮沉和点头加速度的均方根均有所降低，但是当阻尼增大到3 000 N·s/m及以上时，其对电机的振动和点头的影响有限。

4 结论

1）除电机悬挂刚度采用0.1MN/m外，架悬电机的刚度和阻尼对车体的振动响应很小，而工程实际当中，电机悬挂刚度远大于该值，故可以忽略电机悬挂参数对车辆系统动力学性能的影响。

2）电机悬挂刚度和阻尼对构架的振动略有影响，工程上电机悬挂刚度和阻尼一般都较大，因此其对构架振动影响有限。

3）电机悬挂刚度和阻尼对其自身的振动影响相对显著，随着刚度和阻尼的增大，电机的振动加速度RMS均显著降低，然而当刚度增大到2 MN/m以上后其影响减弱。

综上，电机悬挂应当避免过小的悬挂刚度和阻尼，如果采用橡胶元件进行悬挂，应避免橡胶元件老化导致刚度和阻尼损失过大。

参考文献：

[1]曾京，罗仁.考虑车体弹性效应的鐵道客车系统振动分析[J]. 铁道学报，2007，29（6）： 19-25.

[2]黄彩虹，曾京. 基于约束阻尼层的高速客车车体弯曲振动的抑[J]. 交通运输工程学报，2010，10（1）： 36-42.

[3]李凡松，王建斌，石怀龙，等. 动车组车体异常弹性振动原因及抑制措施研究[J]. 机械工程学报，2019 （12）： 20.

[4]王旭嘉. 牵引电机架悬方式对高速动车动力学性能影响研究[D].成都：西南交通大学，2016.

[5]黄彩虹，梁树林，曾京，等.牵引电机架悬参数对动车转向架稳定性的影响[J].铁道车辆，2014，52（11）：1-5，45.

[6]姚远，张开林，张红军，等.机车驱动系统弹性架悬的机理与应用研究[J].铁道学报，2013，35（4）：23-29.

[7]翟婉明. 车辆-轨道耦合动力学[M].4版.北京： 科学出版社，2015.

[8]European committee for standardization. EN 12299. Railway applications ride comfort for passengers measurement and evaluation[S]. Brussel：European Committee for Standardization CEN，2009.

[9]Traction and rolling stock committee， International Unionof Railways. UIC 513. Guidelines for evaluating passenger comfort in relation to vibration in railway vehicle[S]. Paris：Traction and Rolling Stock Committee，1994.

[10]DUMITRIU M. Influence of suspended equipment on the carbody vertical vibration behaviour of high-speed railway vehicles [J]. Archive of Mechanical Engineering， 2016， LXIII（1）： 145-162.