迎角对NACA63-618型机翼力学特性影响研究

罗金武 郑向华 滕鹏 范煦 张博扬

摘要：为探究机翼迎角参数对力学特性的影响，采用流固耦合的数值模拟方法，实现对NACA63-618型等截面机翼的流场和结构的耦合模拟，并对不同设计迎角下的机翼进行力学特性影响分析。数值模拟结果表明，因翼面形状而产生的升力对机翼的变形起着主要作用，在迎角为6度的情况下，NACA63-618型机翼升阻比相对较高，且拥有合理的压力分布，利于升力的产生和高速下的稳定性飞行。

关键词：NACA63-618翼型;等截面;迎角设计;流固耦合;数值模拟

中图分类号：V211.41+2 文献标志码：A

文章编号：2095-5383（2020）04-0023-07

The Influence of Angle of Attack on the

Mechanical Properties of NACA63-618 Airfoil

LUO Jinwu， ZHENG Xianghua， TENG Peng， FAN Xu， ZHANG Boyang

（School of Intelligent Manufacturing，Chengdu Technological University， Chengdu 611730，China ）

Abstract：

In order to explore the influence of parameters of angle of attack on mechanical properties， the numerical simulation method of fluid-solid coupling was used to realize the coupling simulation of flow field and structure of NACA63-618 airfoil with constant cross section， and and the mechanical properties of airfoil under different angles of attack was analyzed. The numerical simulation results show that the lift generated by the shape of the wing surface plays a major role in the deformation of the wing.. When the angle of attack is 6 degrees， the lift-drag ratio of the wing is relatively high， and has a reasonable pressure distribution， which is conducive to the generation of lift and stable flight at high speed.

Keywords：NACA63-618 airfoil; constant section; angle of attack design; fluid-solid coupling; numerical simulation

固定翼飞行器中的机翼属于核心部件，机翼特殊的截面翼型是产生飞行升力的主要来源。而机翼结构与位置布局直接影响了飞行器的力学特性。因此，需多方面考虑机翼选型和几何参数设计问题来保证力学特性的稳定和提升。其中，飞行迎角就是一项重要的几何设计参数，迎角是机翼前、后缘端点的连线（弦线）与飞行方向所形成的夹角，亦称之为攻角。迎角的大小将直接影响到飞机的飞行特性[1]。所以，对于迎角设计的研究至关重要。

实际飞行过程中，机翼周围的空气呈现复杂而多变的流动状态，这种不稳定的环境因素和机翼自身的特殊性导致了理论研究的困难。尤其对于机翼与空气相互扰动的耦合场景，理论研究中的非线性化程度急剧增大，探求理论解析指导实际设计更是难以实现。目前，工程上常采用风洞试验的方法[2-3]，利用精细化的传感监测仪器和设备获取的机翼周边流场分布以及翼面受力的实验数据，来试验分析机翼的最佳设计迎角。但是，风洞试验运行操作难、周期长、成本高、对试验场地基础设施也有着极高的要求，难以实现试验的普及化。

随着计算机技术的不断完善，数值模拟仿真技术[4-5]给机翼流场分析带来了更为经济有效的研究手段，在指导机翼结构与飞行参数设计方面起到了重要作用[6-7]。本文采用流固耦合（Fluid-structure Interaction，FSI）数值模拟方法，以计算流体力学（Computational Fluid Dynamics，CFD）模拟

求解机翼周围流场状态（如压强、马赫数、升阻比

等），以计算固体力学（Computational Solid Mechanics，CSM）模拟求解固体机翼力学状态（如应力、应变等），实现了对NACA63-183型等截面机翼在不同迎角下力学特性的数值模拟仿真，用以指导高速飞行下的最佳飞行迎角，为机翼力学特性的研究提供了参考。

1 研究对象与方法

1.1 NACA63-618翼型

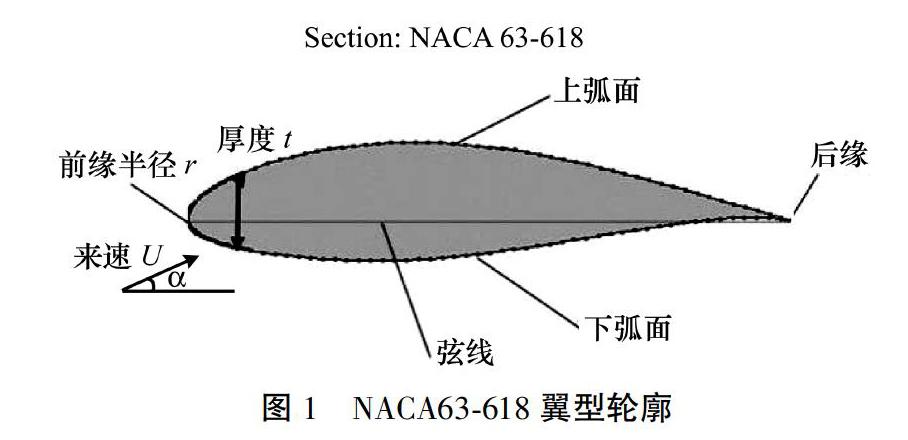
NACA63-618翼型作为美国国家航空咨询委员会（NACA）开发的NACA系列翼型之一[8]，属于层流设计翼型。相对于普通翼型而言，NACA63-618翼型前缘半径更小，翼型最大厚度的位置后移，同时机翼上弧面线形更为平坦，使机翼表面流过的高速空气能够形成较大范围的层流流动，从而减少飞行摩擦阻力。因此，该翼型在高速运行的固定翼飞行器上得到了广泛的应用。

根据NACA提供的翼型生成软件获取如图1所示的NACA63-618翼型輪廓，翼型参数具体含义如图2所示。

1.2 流固耦合

流固耦合计算包含流场分析计算和结构分析计算[9]。利用数值仿真软件STAR-CCM+，将稳态求解后的机翼周围空气压力和速度等数据传递到机翼表面上进行应力、应变单向流固耦合分析，从而获取有用信息。

机翼周围流体的运动遵循质量守恒、动量守恒和能量守恒三大守恒定律[10]。

其中，质量守恒方程为：

其中：u为流体运动速度;F为外力;p为压力;μ为动力黏性系数。

依据弹性力学基本原理，机翼结构力学建立在3个基本方程上：平衡微分方程、几何变形方程以及应力-应变方程（本构关系）[11]。受到流场与自重作用，机翼发生位移变化，基于有限元法构建结构动力学控制方程[12]为：

Msd2δdt2+Csdδdt +Ksδ +  fs=0（3）

其中：Ms为固体质量矩阵;Cs为阻尼矩阵;Ks为刚度矩阵;δ为固体位移; fs为固体受到的外部载荷。再对3个基本方程进行数值求解，即可得到应变、应力和位移的结果数据[13-14]。

流固耦合中计算信息的传递在空气流体计算域与机翼固体计算域形成的交界面中完成[15]。

1.3 力学特性指标

1.3.1 升力系数

升力系数主要用于衡量飞机的举升特性，也称举力系数，是无量纲量，是指飞机所受升力与气体动压及参考面积的乘积之比。定义式为：

CL=L0.5ρV∞2l

（4）

其中：CL为升力系数;L为升力;

V∞

为来流速度;l为特征尺度，对于飞机而言，一般用参考面积（机翼面积）表示。

1.3.2 阻力系数

阻力系数主要用于衡量飞行受阻程度，是无量纲量，是指飞机所受阻力与气流动压和参考面积的乘积之比。定义式为：

Cd=d0.5ρV∞2l（5）

其中：Cd为阻力系数;d为阻力（阻力与来流速度方向相同，向后为正）。

1.3.3 升阻比

升阻比是指升力系数与阻力系数之比，是正常飞行时对飞机力学特性的综合反映。升阻比越高说明机翼获取大升力的同时受阻越小，更有利于力学特性的提高。

1.3.4 压力系数

压力系数是一个无量纲数，它描述流体动力学中遍布整个流场的相对压力，可用于研究机翼关键位置处的压力分布情况。定义式为：

Cp=p0.5ρVSymboleB@2（6）

其中：Cp为压力系数。

1.3.5 失速迎角

达到最大升力系数时所对应的迎角称为失速迎角。当迎角过大超过失速迎角时，机翼上弧面的气流流线无法连贯，层流流动受到的扰动增强，导致机翼上表面后缘方向出现较大范围的流动分离现象，形成封闭的涡流，即分离涡。大尺度分离涡的出现将使上下翼面压差大幅度减小，机翼升力急剧下降，飞行控制也将失灵，导致失速。

2 数值模拟

2.1 几何模型

忽略机身尺寸对机翼周围空气流动的影响，结合对称性的数值模拟方式简化几何模型来建立单个机翼的分析计算域。根据NACA63-618翼型轮廓建立三维、等截面的飞机机翼模型和相对应的流场区域模型。如图3（a）所示，机翼总长4 m，弦长1 m，翼根位于对称面。图3（b）的流场区域模型利用布尔减运算生成，由来流入口、出口、远场、对称面和耦合边界所围成。为保证数值计算的精度和稳定性，让机翼周围气体流动状态充分发展而达到计算的收敛，建立的入口截面为圆弧形，入口最远端距离机翼前缘垂直距离为17 m，出口距离前缘垂直距离25 m，流体区域总高度30 m，宽度10 m。机翼模型与流场模型耦合边界（接触面）需完全贴合，用于数据的准确传输。

2.2 边界设置和网格模型

将几何模型导入STAR-CCM+分配出流体域和固体域，指定基本的边界类型。在耦合边界上流体与固体的求解设置为无滑移壁面Wall，并建立交界面Interface。固体区域的翼根边界为壁面Wall，并设定其为固定端。流场区域的对称面边界为对称平面Symmetry Plane，入口、出口和远场边界均为自由流动Free Steam，并设定自由流方向（1，0，0），马赫数0.8，压强101 325 Pa。

如图4（c）所示，采用STAR-CCM+独有的多面体网格自适应技术进行机翼和流体区域的网格划分。为保证计算精度，对气体流动较为复杂的区域进行网格细化，如图4（a）所示，依次在机翼外围建立近壁加密区和过渡加密区。为机翼边界处划分出棱柱层网格，且第一层网格法向高度为0.1 mm，棱柱层边界层网格步长增长率为1.2，如图4（b）所示。

对计算结果进行网格无关性验证，最终获取的流体区域网格单元为6 392 321个，机翼固体网格单元为37 186个，翼型表面的y+值均小于1，满足翼型气动模拟对计算网格的要求。

2.3 物理模型

流体设置为300 K的空气，密度为1.177 kg/m3、动力黏度为4.58 ×10-5 Pa·s、迎风来速为0.8 Ma（约277.7 m/s），重力加速度9.81 m/s2。迎角取0° ～16° 计算升阻比。假设流体为理想气体，进行三维稳态计算，采用适合于跨音速数值模拟的标准Spalart-Allmaras湍流模型[16]，并使用所有y+壁面处理模型对边界层的第一层网格进行模拟计算。

假设机翼为线性各向同性弹性固体应力材料，考虑自重，机翼密度为7 850 kg/m3、弹性模量为2×1011 Pa、泊松比为0.3，屈服极限为250 MPa，强度极限为460 MPa。在三维、稳态计算中使用有限体积固体应力模型（finite volume solid stress model）求解整个机翼的应力状态。同时激活流体与固体的单元质量校正模型（cell quality remediation model），以限制劣質单元对求解的影响。

采用上文的数值模拟方法对机翼进行气动力学分析，所获结果的可靠性和精度已在多种翼型的计算流体力学问题以及流固耦合问题的研究中得到验证，文献[16]说明了具体的验证过程。

2.4 流场计算与分析

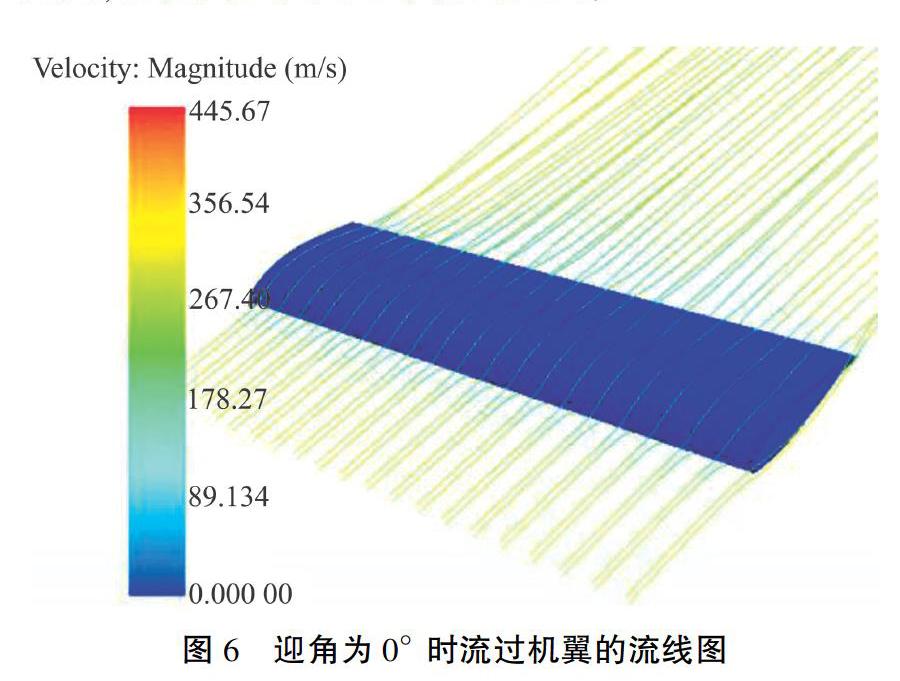
以迎角为0° 时为例，在STAR-CCM+中首先冻结固体应力求解器后进行CFD计算，经过后处理可以观察流场作用在机翼边界处的压力、流过机翼的流线以及距离翼根2 m处截面的马赫数云图，如图5、图6和图7所示。

从图5的压力云图可以看出，最先与来流接触的机翼前缘所受的气体压力最大。机翼上表面中的上缘（厚度较大处）压力远小于下缘处压力，依据伯努利方程，可以推出在机翼的近壁面上缘处的流速更大，这在图6和图7中得到证实。

从图6的流线图可以看出，高速飞行的情况下，流过NACA63-618翼型的流体为层流流动，从而可减少摩擦阻力，层流流动与该翼型的设计特点是一致的，数值模拟结果与实际情况相吻合。分析图7，最大马赫数（流速）位于机翼上弧面靠近后缘的位置，该处拥有较大的速度梯度，会发生层流向湍流的转变，易出现分离涡。

2.5 机翼结构计算与分析

以迎角0° 为例分析，加载机翼翼根处固定端约束，如图8所示，将流体计算的结果通过流固耦合边界直接传递至机翼固体结构中进行求解，此时要求冻结流体域的求解器，解冻固体应力求解器。进而计算获取位移、应力、应变分布情况。

从翼根处开始外伸部位的位移不断增加且最大位移位于机翼的自由端，如图9所示，位移方向总体朝向机翼上方，说明升力足以克服机翼自重。观察图10的应力分布图，可以发现作为悬臂梁的机翼，最大应力位于机翼翼根处，同时在此处出现最大应变，如图11所示，但最大应力点并非因为机翼迎风阻力大而出现在翼型的前缘或后缘，而是位于翼根处的上部，说明因翼面形状而产生的升力对机翼的变形起着主要作用。

3 迎角影响分析

3.1 升力、阻力与升阻比

利用STAR-CCM+中的報告功能，输入101 325 Pa参考压力、277.7 m/s参考速度以及1.177 kg/m3参考密度和受力方向即可分别生成升力或阻力的监测图像和数据，进而获取升阻比。

在设定的迎角范围内，随迎角的增加，升力系数、阻力系数均呈现递增趋势，如图12所示，说明还未达到失速的状态，迎角的增加提高了飞机的举升特性同时增加了飞行阻力。但是分析升阻比曲线则是先增大后减小，在迎角为4° ～8° 附近达到最大值，约4.204～4.457左右，说明4° ～8° 的飞行迎角更有利于提高飞机在高速运行下的综合气动力学特性。

3.2 翼型截面的压力系数分布

流场中机翼各个横截面上的压力分布呈现一致性，如图5所示，故可用距离翼根2 m处的横截面为分析对象，监控、对比不同迎角上下翼型的压力分布情况，获取的压力系数沿翼型分布，如图13所示，迎角较小时，上下翼面的压力分布存在交叉部分，导致机翼上下压差不明显，进一步说明小迎角下的升力较小，不利于飞机举升和高速飞行。对比发现，当迎角达到或高于6° 时，翼面压差分明，能产生足够的升力使得飞机平稳飞行。但是，随着迎角的不断增加，机翼后缘处流体边界分离的情况越发严重，如图14所示，边界分离的起始点不断向前缘移动，导致气体来流的分离涡提前产生，这就增大了飞机失速的可能性。故迎角既不能过小也不能过大，取6° 左右较为合理。

3.3 机翼最大应力、应变以及变形量监测

根据不同迎角下的监测数据，可以列出机翼的最大应力、最大应变以及最大变形数值，见表1。分析可知，机翼的最大应力应变和位移都随迎角的增大而增大，且均在许用范围之内，在一定程度上说明了飞机结构的强度、刚度均能够满足要求。

4 结论

综合考虑飞机的实际飞行情况，采用数值模拟仿真的方法实现了对NACA63-618型等截面机翼的流场和结构的耦合模拟，并对不同设计迎角下的机翼进行力学特性影响分析，结论和建议如下：

1）飞行中机翼承受的最大应力、最大应变点位于翼根处上部，机翼外伸部分向上变形发生位移且机翼自由端位移最大，因翼面形状而产生的升力对机翼的变形起着主要作用。

2）在迎角为4° ～8° 度附近机翼升阻比达到最大值，约4.204～4.457左右，有利于提高飞机在高速运行下的综合力学特性。

3）综合机翼周围流场状态和机翼结构力学状态，分析认为迎角6° 的情况下，机翼升阻比相对较高，且拥有合理的压力分布有利用升力的产生，在0.8 Ma的飞行状态下，其尾流边界分离起始点相对靠进后缘，分离涡不明显，这会降低机翼的颤振，也不易发生失速。

4）建议在安装NACA63-618型机翼时，选择6° 作为弦线与水平面的安装角度，起飞时的长距离加速可以使得飞机尽快达到高速状态。升空时虽有迎角以小角度的增加，但是根据图13中的压力分布数据，可以发现迎角的增加使得机翼上下面压力差的显著分布，更有利于飞机的上升运动，并且不会出现失速的状态。待到飞机达到设定高度和飞行速度，即回到设计的迎角，稳定前行。

参考文献：

[1]李其轩.探究迎角对机翼升力的影响及“失速”现象的解释[J].内燃机与配件，2018（5）：209-210.

[2]FAUCI R， NICOLIA， IMPERATORE B， et al. Wind tunnel tests of a transonic natural laminar flow wing[C].American Institute of Aerodynamic and Astronatutics. 25th AIAA Aerodynamic Measurement Technology and Ground Testing Conference. San Francisco： AIAA，2006.

[3]许新，陈德华，程克明，等.大展弦比飞机变翼展洞壁干扰试验与分析[J].南京航空航天大学学报，2019，51（4）：519-525.

[4]MOHAMED M D， WAEL T， MONDHER Y， et al. Numerical

investigation on aircraft wing stiffener composite material integration [J]. Aerospace Systems， 2019，2（2）：137-145.

[5]HUA X，SHAO W，ZHANG C H， et al. Base on imitation seagull airfoil UVA wing numerical simulation [J]. Applied Mechanice and Material，2012，3（1）： 323-326.

[6]杜春志，傅博宇，邱致浩.某型低速飞机复合材料机翼的设计与有限元分析[J].机械设计，2019，36（S2）：55-58.

[7]张义浦，張志春，赵秀影.基于FLUENT的飞机机翼积冰的数值模拟[J].科学技术与工程，2017，17（20）：302-307.

[8]XIEHR， WU YD， OUYANG H， et al. Erratum to： experimental

investigation on a single NACA airfoils nonlinear aeroelasticity in wake induced vibrations [J]. Fluid Dynamics，2019，54（5）：740.

[9]雷晓珊，马勇，蔺世杰.基于单向流固耦合的不同风速下帆板帆翼空气动力性能仿真[J].武汉体育学院学报，2019，53（11）：95-100.

[10]王福军，计算流体动力学分析CFD软件原理与应用[M].北京： 清华大学出版社，2004.

[11]刘超峰，邱菊.气动弹性的流固耦合分析方法[M].北京：北京航空航天大学出版社，2016.

[12]蒋树杰，刘菲菲，陈刚.流固耦合振动效应对机翼气动噪声辐射的影响研究[J].振动与冲击，2018，37（19）：7-13.

[13]王文全，张立翔.计算流固耦合动力学及其应用[M].北京：中国水利水电出版社，2015.

[14]徐敏，安效民，陈士橹.一种CFD/CSD耦合计算方法 [J].航空学报，2006，27（1）： 33-37.

[15]ZHOU Q，LI D F，RONCH A D，et al. Computational fluid dynamics-based transonic flutter suppression with control delay[J]. Journal of Fluids and Structures，2016，66：183-206.

[16]Siemens PLM Software Inc. STAR-CCM+： user guide，version 12.02 [M]. Plano： Siemens PLM Software Inc.，2017.