传感器在炉管泄漏检测互相关算法中的影响

彭小兰1，刘志强2，黄霄2

传感器在炉管泄漏检测互相关算法中的影响

彭小兰1，刘志强2，黄霄2

(1. 湖南省特种设备检验检测研究院，湖南长沙 410111；2. 中南大学能源与动力工程学院，湖南长沙 410083)

将互相关算法应用于炉管泄漏定位中，搭建了一套基于时延测量的炉管泄漏检测系统。时延值是通过传感器相位差计算出来的，传感器的初始相位差以及节点位置都会影响检测结果。实验结果表明：(1) 基于互相关算法的锅炉管泄漏定位系统中的4个传感器的初始相位需要进行一致性匹配；(2) 对子脉冲信号，时延测量不受传感器之间距离的影响；但是对周期性信号，只有在传感器间距对应的时延小于半周期时，互相关算法才能准确计算出时延值；(3) 传感器尺寸小于50 mm时，采用互相关算法测量时延才准确。

泄漏；互相关算法；时延值；传感器；相位差

0 引言

国外早期的锅炉泄漏检测系统体积庞大，结构复杂，调试繁琐，且检测精度、运行可靠性、报警准确率都较差，并且不能进行泄漏的定位[1-3]。近年来，炉管在线泄漏监测装置依靠密集的传感器布置以感知泄漏噪声进行区域性定位，仍存在施工复杂、成本高、定位难的局限性[4-6]。本文设计搭建了一套基于互相关算法的炉管泄漏判定与定位的实验系统。在锅炉管泄漏定位领域，对比互相关算法、波束形成法[6]和高分辨率谱估计法[7-8]三种计算方法，用互相关算法来计算时延值时，需要的传感器最少，定位最精准，现场最为适用。时延值为不同位置传感器接收到某一时刻声源的时间差，结合传感器位置、声速即可对声源位置进行求解。因为时延值的获取是通过相位角的差值来计算得到的，所以定位中最关键、最重要的一个设备是传感器，而在互相关算法中最重要的参数就是传感器的初始相位、相位差及位置。本文具体分析了这三个因素对定位的影响。

1 互相关算法

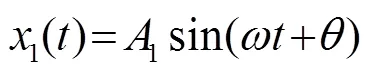
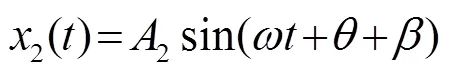
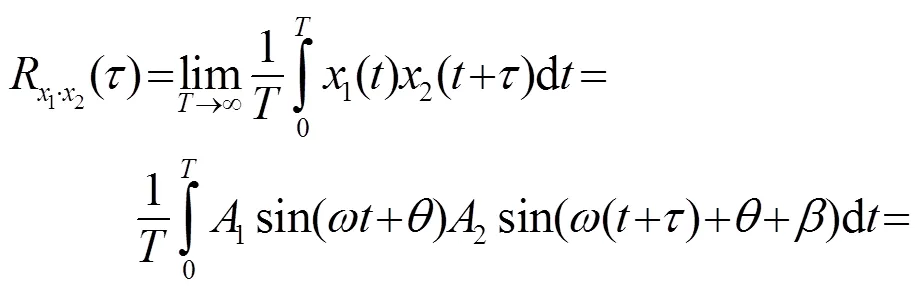
式中：为样本信号的时间长度。

2 实验系统

为了验证互相关算法是否能准确定位并研究影响定位的因素，本文设计并搭建了一套声学定位系统。系统硬件主要有声学传感器、高速数据采集卡、SMB线缆、ICP供电器、便携式工控机。设备选型时声学传感器4个为一组，高速数据采集卡需达到20 kHz以上的采样率并且各通道同步采样，同步传输数据。SMB线缆接口接触良好、稳定。满足以上选型要求的设备是正确采集时延值的基础；系统软件包括数据采集控制界面，用于调节采样率及采样点数。基于MATLAB的互相关程序，对两路信号进行相关分析，自动计算时延值；定位程序，给出声源坐标。实验平台硬件系统的结构图如图1所示。

3 传感器在实验中的影响及分析

传感器阵列引入了声源的位置信息，同一声音到达不同位置传感器的时间(相位)不同，结合传感器之间的几何位置，理论上可以解出声源坐标。阵列中传感器的位置决定了其特点，目前有均匀直线阵列、均匀圆阵列和四面体阵列。以四面体阵列为代表的空间阵列相较于平面阵列的最大优势在于无定位盲区，且不仅能对声源实现方位估计，更能实现精确到坐标点的位置估计。四面体阵有正四面体阵、直角四面体阵、不规则四面体阵三种，从便于安装、设置传感器及定位算法复杂度考虑，选择直角四面体阵列，如图2所示。得到时延值后，声源就处于以这对传感器所处的位置为焦点、时延值所对应的声音传输距离为参数的双曲面上。使用多对传感器得到多个时延值，从而得到多个双曲面。由于阵列形式和随机误差的影响，多个双曲面的交点可能是空集，采用最优化的思想进行求解。

图2 直角四面体阵列(Mi表示传感器，S表示声源)

在自由场条件下，不考虑传声器对声场影响，得到的定位方程如下：

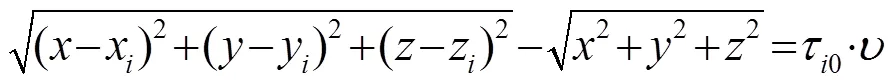
本文采用自由场声音传感器，它测量到的是消除了传感器对声场影响的声压，其基本性能参数如表1所示。

表1 传感器性能参数

3.1 传感器初始相位匹配

为了验证声音传感器的相位是否匹配，将声源置于空间一点，通过改变传感器之间的距离，观察其相位差变化。共做3组实验，将频率统一设置为10 kHz，声速为340 m·s-1。第1组，传感器的间距为0.3 m；第2组，传感器的间距为1.0 m；第3组，传感器的间距为2.0 m，其时延值如表2所示。

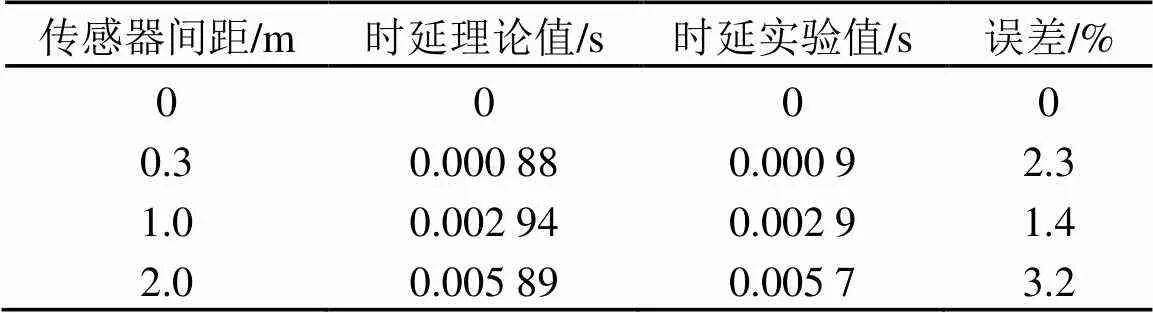
表2 不同传感器间距的初始相位差

由表2可知，传感器初始相位差的实验结果与理论值的误差在4% 范围内，认为实验平台所采用的声音传感器相位匹配度较好，可以进行下一步的实验。

3.2 传感器之间相位差的影响

不论采用何种阵列形式和定位算法，都需要多个传感器对同一段声音进行精确采样。这要求对声音进行同步采集，即使用同一个采样脉冲序列对多个传感器获取的声音信号进行量化。1924年，奈奎斯特就提出当采样频率大于信号中最高频率的2倍时，釆样之后的数字信号会完整地保留原始信号的信息。人耳的听力极限是44.1 kHz，根据奈奎斯特采样定理，采样率只要达到100 kHz，采集到的声音就不会失真。相邻阵元之间利用互相关算法获取时延的过程中，其准确程度与声源频率以及声音传感器之间的相对距离有关。

3.2.1 相位差对脉冲信号的影响

对于频率为2 500～3 000 Hz的脉冲信号用信号发生器生成单个脉冲信号，再用互相关函数进行分析、处理，脉冲信号及其互相关波形如图3所示。

由图4可以看出，当声源为脉冲信号时，用互相关算法计算时延值很准确；无论相位差增大或减小，都不会对时延值结果产生影响。这是因为脉冲信号，可以认定为周期无限长的周期函数或者采样频率无限大的周期函数，所以不会对时延值产生影响。

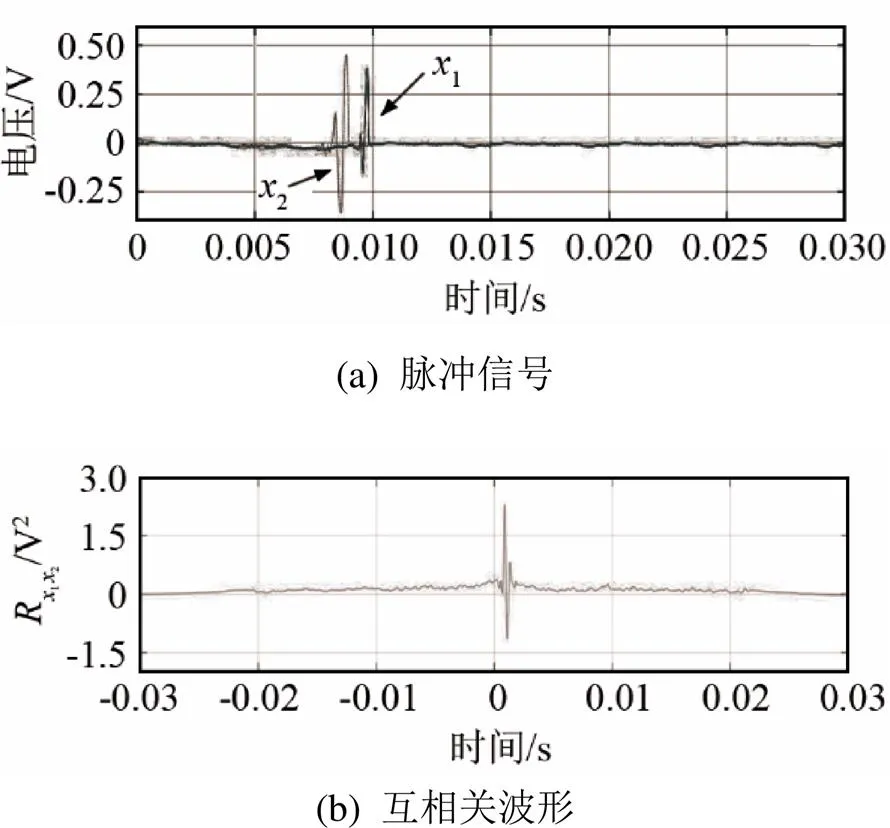
图3 脉冲信号及其互相关波形

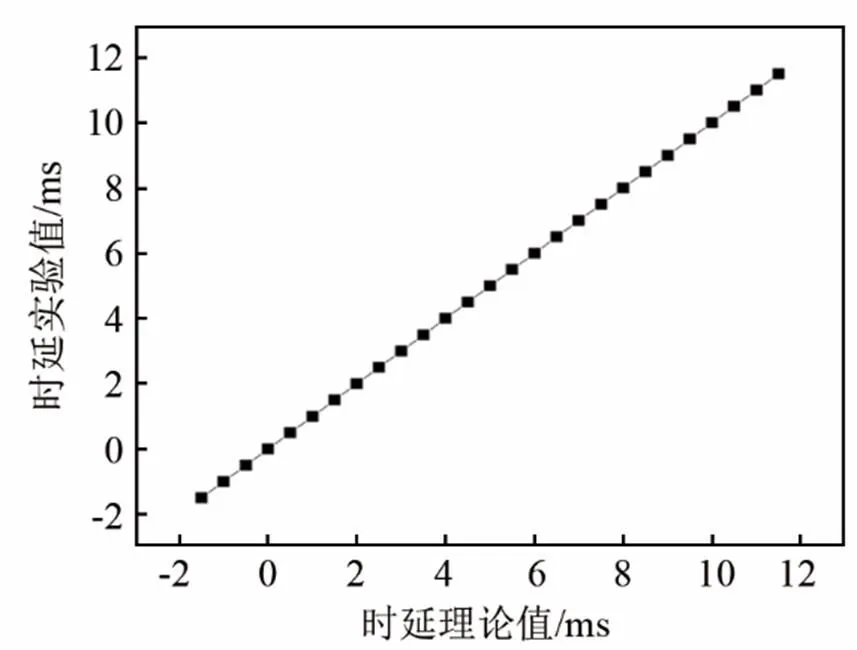
图4 脉冲信号时延计算和实验结果比较

3.2.2 相位差对连续周期信号的影响

信号发生器生成频率为2 500～3 000 Hz的连续周期信号，用互相关函数进行分析、处理，得到的结果如图5所示。

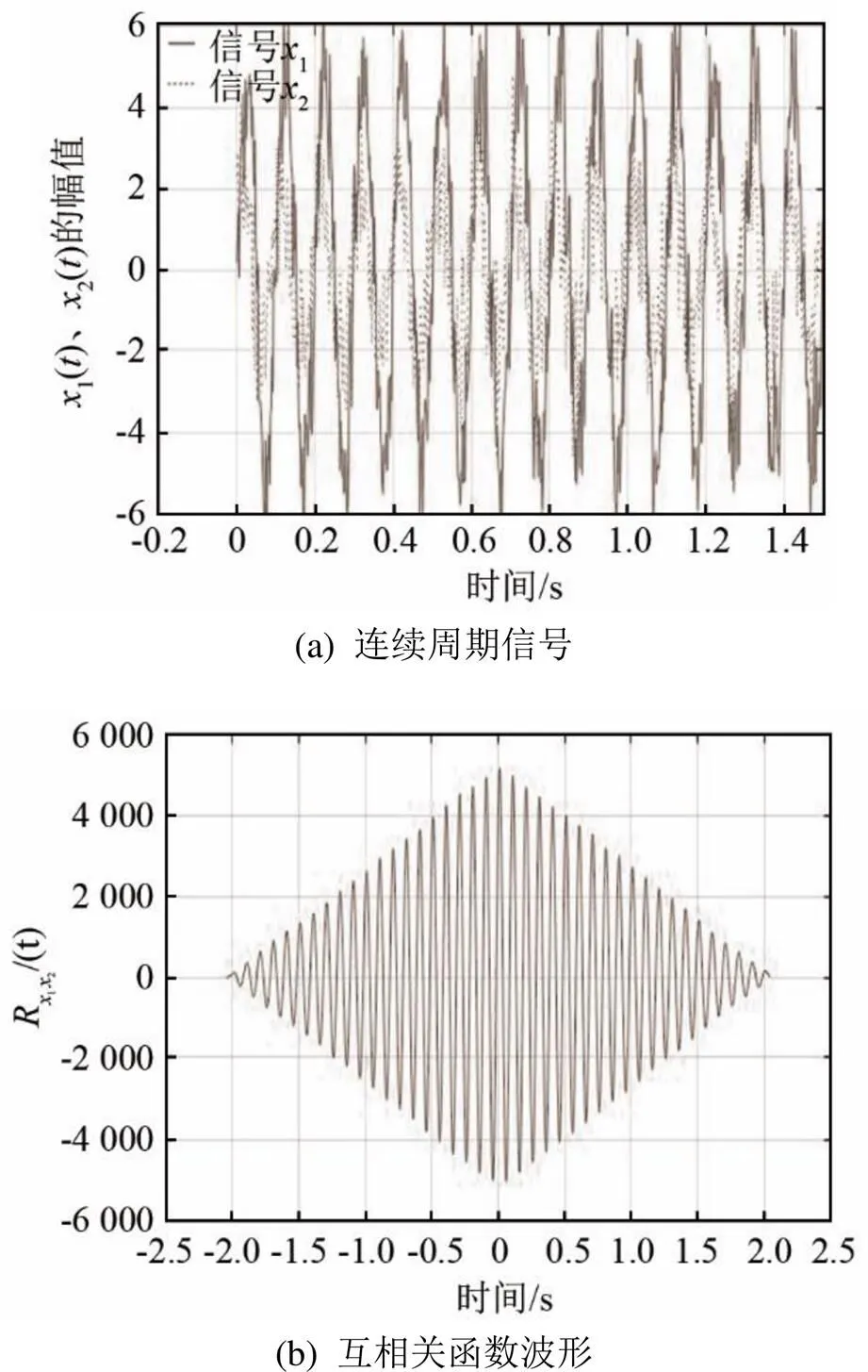
图5 连续周期信号及其互相关波形

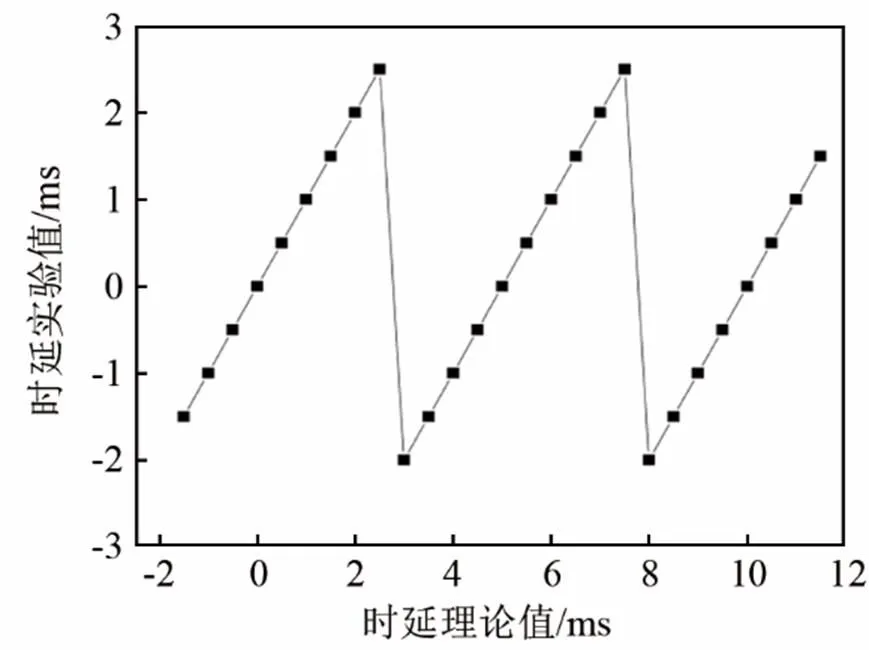
图6 连续周期信号时延计算和实验结果比较

令：

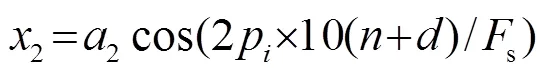
表3 互相关算法的时延计算结果

以上的数据与图像表明：

(1) 在＜50时，互相关函数峰值明显，时延点数计算准确。

可得出结论：互相关算法只有对延迟时间小于一个信号周期的两路信号进行时延估计才是准确的，否则将出现互相关峰重叠问题。另一方面，在传感器之间相对位置已经固定的情况下，声源的频率越低，获取的时延值越准确；当环境有噪声存在时可以先进行带通滤波再做互相关运算，从而保证定位精度。在声源频率固定的情况下，传感器之间的距离不能大于声源信号的波长，在实验中常设置为不能大于声源信号的半波长。

3.3 传感器阵列尺寸校准

从定位方程式(4)可以看出，定位结果还受传感器阵列尺寸的影响。通过在程序中增加传感器阵列尺寸的数值，计算定位结果的误差变化，如图7所示。

结果表明：在不考虑其他误差的情况下，传感器阵列尺寸的测量误差越大，定位结果的误差也越大。当传感器阵列尺寸的测量误差在1%～10%区间变化时，定位结果、、方向的误差分别由2.5%、2%、3.2%增大到16.5%、13.3%、19.2%。

因此，实验时有必要对声音传感器实际位置进行校正。首先在测试区域内某已知点发声，记录测点位置。接着调整定位程序中传感器间距的大小，调整范围不超过±50 mm，直到输出的定位结果与实际测点位置良好匹配。记录此时阵列间距，即为校准后的实际传感器间距。为保证传感器阵列尺寸的准确性，可以采取多个已知点进行校准。

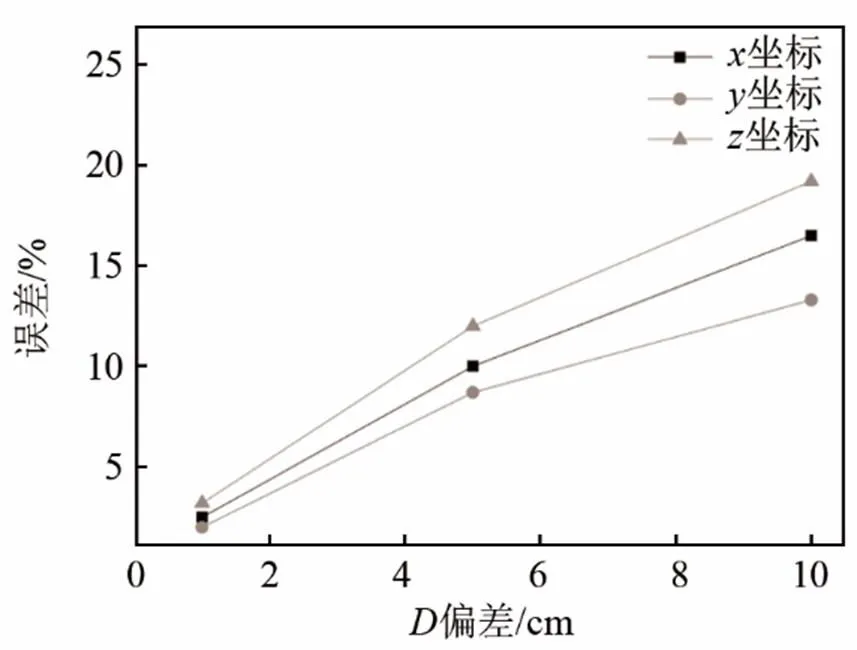
图7 传感器阵列尺寸D的测量误差对定位结果的影响

4 结论

(1) 为保证基于互相关算法的锅炉管泄漏定位系统时延测量结果的准确性，实验中的4个传感器需要进行初始相位的一致性匹配和校准；

(2) 分析互相关算法求取时延值的适用对象：针对脉冲信号，互相关算法的峰值明显，计算结果与理论结果吻合较好；针对连续周期信号，互相关算法没有明显的峰值，计算结果呈现出一个周期性的变化规律，可以表示为(为整数)，与理论结果相差整数倍/2。

(3) 阵列尺寸的测量误差对定位结果的影响：阵列尺寸校准前后，定位结果会发生很大改变，阵列尺寸校准后，定位结果的准确度会有很大提升。传感器作为质点对象研究，只有传感器阵列尺寸小于50 mm时，基于时延的互相关算法才准确。因此，进行声源定位时，需要对阵列尺寸进行校准。

[1] NARAYANANV N H, VISWANAD-HAM N. A methodology for knowledge aequisition and reasoning in failure analysis of systems[J]. IEEE Trans. Systems Man Cyberneties, 1987, 17(3): 274-288.

[2] ZHANG Y, LIANG F, SU F. A fuzzy production rule expert system[J]. Fuzzy Sets and Systems, 1991, 44(3): 291-310.

[3] LUO R, MISRA M, HIMMELBLAU D. Sensor fault detection via multiscale analysis and dynamic[J]. PCA. Ind. Eng. Chem. Res. 1999, 38(4): 1489-1495.

[4] BRANDSTEIN M S, SILVERMAN H F. A practical methodology for speech source localization with microphone arrays[J]. Computer, Speech and Language, 1997, 2(11): 91-126.

[5] 杨卫娟, 周俊虎. 锅炉管道泄漏知识及应用现状[J]. 动力工程, 2000, 20(6): 937-940.

YANG Weijuan, ZHOU Junhu. Knowledge and application status of boiler pipe leakage[J]. Power Engineering, 2000, 20(6): 937-940.

[6] 安连锁, 冯强, 沈国清, 等. 电站锅炉管阵列内声传播特性及时延值测量[J]. 动力工程, 2017, 30(1): 937-940.

AN Liansuo, FENG Qiang, SHEN Guoqing, et al. Acoustic propagation characteristics and time delay measurement in power station boiler tube array[J]. Power Engineering, 2017, 30(1): 937-940.

[7] 吕勇兴. 锅炉“四管”泄漏监测系统的研究[D]. 北京: 华北电力大学, 2011.

LYU Yongxing. Research on boiler "four-tube" leakage monitoring system[D]. Beijing: North China Electric Power University, 2011.

[8] 张成辉. 锅炉炉管泄漏检测系统的研究[D]. 沈阳: 沈阳航空航天大学, 2012.

ZHANG Chenghui. Research on boiler tube leak detection system[D]. Shenyang: Shenyang Aerospace University, 2012.

[9] MUNGAMURU B, AARABI P. Enhanced sound localization systemss[J]. IEEE Transactions on., 2004, 34(3): 1526-1540.

[10] NISHIURA T, YAMAD T. Localization of multiple sound sources based on a CSP aanalysis with a microphone array[C]//Acoustics, Speech, and Signal Processing, 2000. ICASSP00. Proceedings 2000 IEEE International Conference on 2000, 2: 1053-1056.

[11] 王琳. 炉内管道泄漏声检测与定位系统的研究现状[J]. 声学学报, 2010, 29(1): 1-10.

WANG Lin. Research status of sounding and positioning system for furnace pipeline leakage[J]. Acta Acoustics, 2010, 29(1): 1-10.

The influence of sensors on the cross-correlation algorithm for furnace tube leak detection

PENG Xiao-lan1, LIU Zhi-qiang2, HUANG Xiao2

(1. Hunan Special Equipment Inspection & Testing Institute, Changsha 410111, Hunan, China; 2. School of Energy and Power Engineering, Central South University, Changsha 410083, Hunan, China)

The cross-correlation algorithm is applied to locating furnace tube leak, and a set of time delay measurement based furnace tube leak detection system is built. The time delay value is calculated by the phase difference. The initial phase difference and the placed position of the sensor will affect the detection result. Experiments show that: 1. the initial phase differences of the four sensors in the cross correlation algorithm based tube leak location system require consistency matching; 2. for impulse signal, the time delay measurement is independent of the sensor spacing, however, for periodic signal, only if the time delay corresponding to the sensor spacing is within half a period, the cross-correlation algorithm can accurately calculate the time delay value; 3. only when the sensor size is less than 50mm, the time delay measurement by cross-correlation algorithm is accurate.

leakage; cross-correlation algorithm; time delay value; sensor; phase difference

TP31

A

1000-3630(2019)-06-0705-05

10.16300/j.cnki.1000-3630.2019.06.018

2018-04-28;

2018-09-09

质检公益性行业专项项目(201510067)、国家自然科学基金(51376198)资助

彭小兰(1979－), 女, 湖南长沙人, 博士, 教授级高级工程师, 研究方向为炉管泄漏检测。

黄霄,E-mail: 463746420@qq.com