相位编码信号声学多普勒测流中的波形参数优化方法
2020-01-19杨永寿方世良
杨永寿,方世良
相位编码信号声学多普勒测流中的波形参数优化方法
杨永寿1,2,方世良1,2
(1. 东南大学水声信号处理教育部重点实验室,江苏南京 210096;2. 东南大学信息科学与工程学院,江苏南京 210096)
针对相位编码声学多普勒测流中发射信号参数固定引起的适应性不强的问题,在基于信号模糊函数及其模的二阶导数的基础上,提出了两种根据测量需求和环境条件调整发射信号波形参数的优化方法,它们是分层精度约束下取得最佳速度估计精度的波形参数优化方法以及测速精度约束下实现最细分层厚度的波形参数优化方法,分别给出了参数优化的原理和具体的操作步骤。理论分析和实验数据分析结果均表明,相对于缺省参数信号,优化参数方法得到的信号具有明显的性能优势,且优化程度与理论预测基本相符。
声学多普勒;模糊函数;相位编码;波形优化;速度估计
0 引言
声学多普勒测流中常用的发射信号有矩形脉冲(Rectangular Pulse, RP)、相干脉冲串(Coherent Pulse Train, CPT)和相位编码脉冲(Phase Modulated Pulse, PMP)[1],分别应用于脉冲非相干测流法(Pulse to Pulse Incoherent, PPI)[2]、脉冲相干测流法(Pulse to Pulse Coherent, PPC)[3]和宽带测流法(Broadband, BB)[4]。根据信号的模糊函数理论[5]和信号处理常识,可以得到以上信号的特性及其适用的应用场景。(1) 矩形脉冲信号的有效带宽与脉冲宽度成反比,因而脉冲宽度越窄其距离或时间分辨能力越强,但频率分辨能力越差。由于脉冲非相干方法的脉冲重复周期和最大可测流速没有关联,所以探测距离、测速范围都可以很大。但是,受其距离分辨率、频率分辨率不可兼得特性的影响,只适用于对分层精度、测速精度要求都不高的场合。(2) 相干脉冲串信号具有钉板状的模糊图,在保证同等带宽条件下大大延长了信号的持续时间,因此既具有矩形窄脉冲的高距离分辨率特性,又具有较高的频率分辨率。但是,其存在距离-速度模糊缺陷,即探测距离和最大可测速度之间相互限制、不可兼得。因此脉冲相干方法一般应用于浅水、细分层、测速精度要求较高的场景。(3) 相位编码信号具有图钉型的模糊函数。距离分辨能力由调制带宽决定,而频率分辨率由脉冲持续时间决定,两者不再相互限制。通过相位编码与脉冲相干技术的结合,在保证探测距离的基础上提高了速度估计的精度,集合了矩形脉冲和相干脉冲串的优势。另外,由于在声学多普勒测流中既需要测速又需要测距,且水体流动引起的多普勒频移相对较小,所以相位编码信号比线性调频信号(Linear Frequency Modulation, LFM)等其它宽带信号更适用于声学多普勒测量。正因为相位编码信号具有以上技术优势,其应用最为广泛。
本文从信号的模糊函数入手,推导了相位编码信号的距离分辨率、速度估计精度与其码元宽度、编码长度和重复次数等波形参数之间的关系。提出了两种适应不同应用场景的相位编码信号波形参数优化方法。(1) 分层精度及目标流速约束下的波形参数优化方法给出了在满足最大允许分层厚度约束条件时实现最大测速精度的波形参数计算方法。此方法适用于较为关心测速精度,而非分层精度的应用场景,比如深浅流速相差不大的均匀流速剖面测量。(2) 测速精度约束下的波形参数优化方法给出了在满足最低允许测速精度约束条件时实现最小分层厚度的波形参数计算方法。此方法适用于较为关心分层精度,而非测速精度的应用场景,比如深浅流速相差较大的非均匀流速剖面测量。以上两种方法实现了多种场景下的测流性能优化,提高了声学多普勒测流设备的环境适应性。
1 测流信号的模糊函数


1.1 窄带信号的模糊函数
窄带信号以矩形脉冲为例。矩形脉冲的复包络定义为

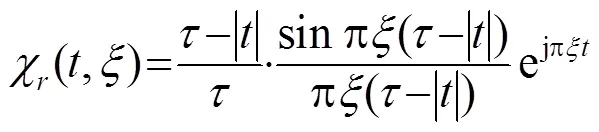
1.2 相位编码脉冲模糊函数
相位编码信号使用一组以不规则间隔出现的1或-1序列,对载波进行相位调制。编码序列的选择标准是其自相关函数在原点出现峰值,离开原点后很快衰减,从而形成一个中心尖峰。相位编码信号分为二相编码和多相编码[6]。二相编码仅有两个可选择的相位状态,通常为0和π。本文仅讨论二项编码的情形。多次重复二相编码信号的复包络可表示为
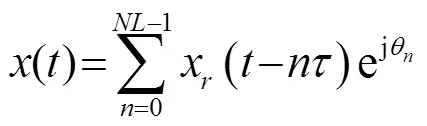
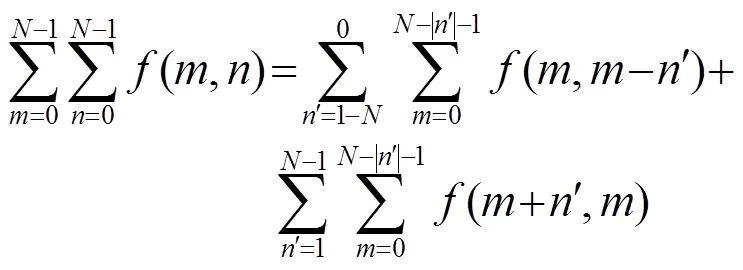
推导得到次重复、位编码脉冲的模糊函数为
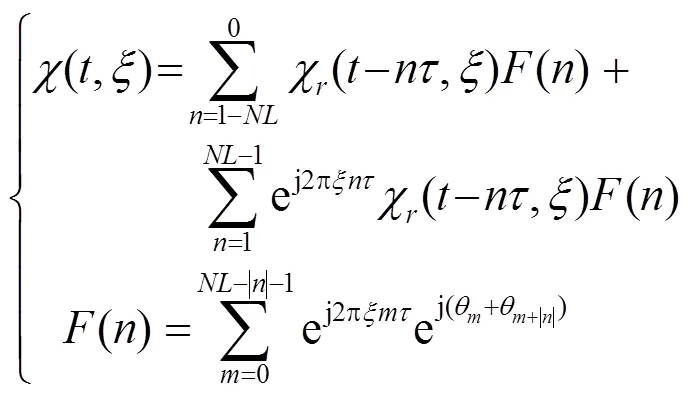
其中,为矩形脉冲的模糊函数,如式(3)所示。由于编码的限制,式(6)的化简程度有限,其图形如图1所示。
2 测流性能代价函数
2.1 距离分辨率


从式(7)可知,相位编码信号的距离模糊函数是由个幅度加权的三角脉冲叠加而成,加权系数由编码序列不同延迟下的自相关特性决定。这些三角脉冲的底宽相同,尖峰幅值不同。
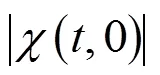

则其距离分辨率为
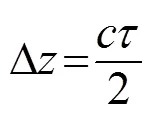
以上分析说明,相位编码信号的距离分辨率只与码元宽度有关,与编码形式无关。也可以理解为码元宽度决定了编码信号的带宽,从而决定了距离分辨率。
2.2 速度估计精度

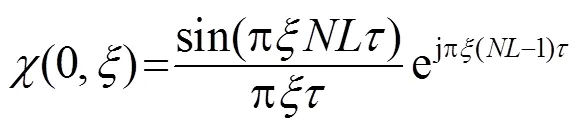


将式(10)代入式(11)中,计算后得到:
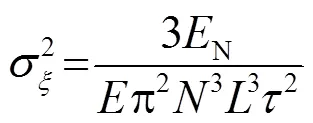
3 相位编码信号的波形参数优化方法
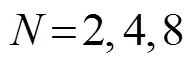
针对实际测流中存在的优先考虑测速精度和优先考虑分层精度两种场景,分别提出了分层精度及目标流速约束条件和测速精度约束条件两种波形参数的优化方法。总的来说,前者是在满足最大允许分层厚度条件下调整波形参数以获得最好的测速精度,而后者则是在满足最低测速精度条件下调整波形参数以实现最细的分层。本节的编码以巴克码为例。
3.1 分层精度及目标流速约束下的波形优化方法

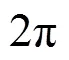
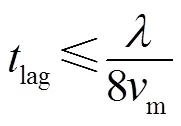


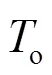

(4) 编码长度,重复次数可以由式(16)确定:

3.2 测速精度约束下的波形优化方法

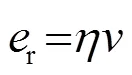


4 实验室数据处理
利用实验室已有的声学多普勒测流岸上测试系统和一台600 kHz ADCP搭建了本方法的验证平台。岸上测试系统产生设定参数的模拟回波,通过换能器的无缝对接模拟ADCP的实测。岸上测试系统由电脑、MATLAB回波仿真软件、任意波形发生器、功率放大器和换能器等组成。平台的实物照片如图3所示。图3左上方是岸上测试系统,右下角是ADCP,左下角是对接起来的换能器。频率为600 kHz的ADCP的系统带宽是100 kHz,编码类型为巴克码二相编码,波束宽度为3°。

图3 实验系统照片
实验方法是同等条件下比较长、短发射波形的测流性能。实验共有两个项目:均匀流速剖面测量和非均匀流速剖面测量。(1) 均匀流速剖面测量实验中各层流速设定为相同数值。理论上长脉冲可以获得更好的测速精度。长脉冲信号参数由第3节中的波形优化方法确定,短脉冲信号参数人为选定。实验中对比了两种脉冲波形在0~40 dB范围内、9种信噪比下的测速性能。每种信噪比条件下,取100次重复测量结果的平均值。(2) 非均匀流速剖面测量实验中各层流速设定在0~2 m·s-1间线性变化,模拟强剪切流场景。理论上短脉冲可以实现更好的分层流速测量。短脉冲信号参数由第3节的波形优化方法确定,长脉冲信号参数人为选定。对比了两种波形的剖面测速结果。
4.1 均匀流速剖面测量实验
岸上测试系统设置为:散射体随机分布,每立方米有105个散射体,线性流速分布且顶层和底层速度均为0.3 m·s-1,编码为巴克码,球形扩展衰减。



图4 长、短脉冲测量均匀流速剖面结果对比
measured by the long pulse and the short pulse
4.2 非均匀流速剖面测量实验
岸上测试系统设置:散射体随机分布,每立方米有105个散射体,线性流速分布且顶层速度为2 m·s-1、底层速度为0,编码为巴克码,球形扩展衰减。

实验的结果如图5所示。实线表示设定分层流速,三角散点表示长脉冲的测速结果,星号散点表示短脉冲的测速结果。由图5可知,短脉冲信号的测点较多,分层精度明显高于长脉冲信号。短脉冲测速结果与设定值吻合较好,长脉冲测速结果虽然围绕设定值波动,但明显更加发散。这是由于长脉冲单层中的流速变化较短脉冲大,测速精度变差。

图5 长、短脉冲测量非均匀流速剖面结果对比
5 结论
在相位编码声学多普勒测流中,发射波形参数直接影响到最终的测流性能。基于信号模糊函数及其二阶导数的推导发现:相位编码信号的距离分辨率由其码元宽度决定,即由信号带宽决定;相位编码信号的速度估计标准差与脉冲宽度的1.5次方成反比。测流中追求高测速精度时在增大信号编码长度、重复次数的同时要考虑分层厚度等约束条件。同理,追求细分层时在减小信号编码长度、重复次数的同时还要考虑测速精度的限制条件。实验室数据分析结果表明,采用本文的优化波形设计方法在均匀、非均匀流速剖面测量中均能明显改善测流精度或分层精度,且改善的程度与理论预测接近。
[1] IVIĆ I R. Effects of phase coding on doppler spectra in PPAR weather radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(4): 2043-2065.
[2] THERIAULT K. Incoherent multibeam doppler current profiler performance: part I--estimate variance[J]. IEEE Journal of Oceanic Engineering, 1986, 11(1): 7-15.
[3] ZEDEL L. Modeling pulse-to-pulse coherent doppler sonar[J]. Journal of Atmospheric and Oceanic Technology, 2008, 25(10): 1834-1844.
[4] BRUMLEY B H, CABRERA R G, DEINES K L, et al. Performance of a broad-band acoustic Doppler current profiler[J]. IEEE Journal of Oceanic Engineering, 1991, 16(4): 402-407.
[5] RICHARDS M A. Fundamentals of radar signal processing[M]. Tata McGraw-Hill Education, 2005.
[6] CHI C, LI Z, LI Q. Design of optimal multiple phase-coded signals for broadband acoustical Doppler current profiler[J]. IEEE Journal of Oceanic Engineering, 2015, 41(2): 302-317.
[7] RIHACZEK A W. Principles of high-resolution radar[M]. Norwood, MA: Artech House, 1996.
[8] 丁鹭飞, 耿富录. 雷达原理[M]. 5版. 北京: 电子工业出版社, 2014.
DING Lufei, GENG Fulu. Radar principle[M]. 5th ed. Beijing: Publishing House of Electronics Industry, 2014.
[9] KAY S M. Detection theory, vol. II of Fundamentals of statistical signal processing[M]. London: Prentice Hall PTR, 2013.
[10] 林伊凡, 陈梦英, 景永刚, 等. 宽带声学多普勒计程仪性能试验分析[J]. 声学技术, 2019, 38(3): 348-353.
LIN Yifan, CHEN Mengying, JING Yonggang. Performance test and analysis of broadband acoustic Doppler velocity log[J]. Technical Acoustics, 1999, 38(3): 348-353.
[11] Teledyne RD Instruments, Inc. RiverRay ADCP Guide[EB/OL]. Poway: Teledyne RD Instruments, 2019[2019-10-10]. http://www. teledynemarine.com/Documents/Brand Sup-port/RD INSTRUMENTS/Technical Resources/Manuals and Guides/RiverRay/RiverRay Getting Started_Jun18. pdf
Optimization of phase coded waveform parameters in acoustic Doppler current measurement
YANG Yong-shou1,2, FANG Shi-liang1,2
(1. Key Laboratory of Underwater Acoustic Signal Processing of Ministry of Education, Southeast University, Nanjing 210096, Jiangsu, China;2. School of Information Science and Engineering, Southeast University, Nanjing 210096, Jiangsu, China)
In order to solve the problem of weak adaptability of the phase coded acoustic Doppler current measurement using the transmitting signal of fixed parameters, based on the signal ambiguity function and the second derivative of its modulus, two optimization methods are proposed to adjust the parameters of the transmitting signal waveform according to the measurement requirements and environmental conditions. One of the two waveform parameter optimization methods is to obtain the best velocity estimation accuracy under the constraint of layered accuracy and the another one is to achieve the most subdivided layer thickness under the constraint of velocity measurement accuracy. The principle and specific operation steps of waveform parameter optimization are given respectively in this paper. The results of theoretical analysis and experimental data analysis show that compared with the signal of default parameters, the signal obtained by the optimized parameter method has obvious performance advantages, and the optimization degree is basically consistent with the theoretical prediction.
acoustic Doppler; ambiguity function; phase coding; waveform optimization; velocity estimation
TN911.7
A
1000-3630(2019)-06-0605-06
10.16300/j.cnki.1000-3630.2019.06.001
2019-10-29;
2019-12-05
中央高校基本科研业务费专项资金资助(2242016K30013)
杨永寿(1985-), 男, 安徽合肥人, 博士研究生, 研究方向为声学多普勒测流技术。
方世良, E-mail: slfang@seu.edu.cn
