Research on adaptive equalization algorithm for sparse multipath channel

LI Wen-yan, ZHU Ting-ting, WANG Qi

Research on adaptive equalization algorithm for sparse multipath channel

LI Wen-yan, ZHU Ting-ting, WANG Qi

(School of Electronic Information Engineering, Xi'an Technological University, Xi'an 710021, Shaanxi, China)

0 Introduction

Inter-symbol interference (ISI) caused by multipath propagation is especially common in underwater acoustic communication and broadband mobile communication[1],which has greatly hindered the transmission of reliable information. In order to offset the inter-symbol interference, the filter needs to adaptively track the change in channel conditions to recover the distortion caused by multipath transmission[2]in the moving environment.

Common underwater acoustic communication and broadband mobile communication are generally sparse multipath channels, that is, the energy of channel impulse response mainly focuses on a few taps with a long interval, and the energy of most taps tends to zero. When the source passes through the channel, inter-symbol crosstalk can be up to dozens or even hundreds of symbol intervals.

1 Adaptive equalization and compression sensing theory

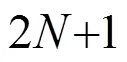
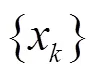
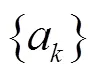
Mean square error is defined as:

According to (1):

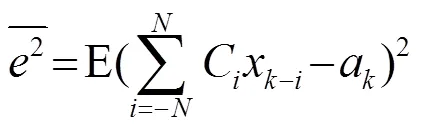
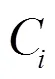
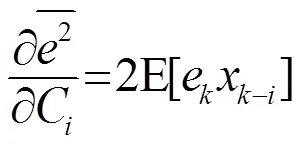
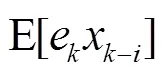
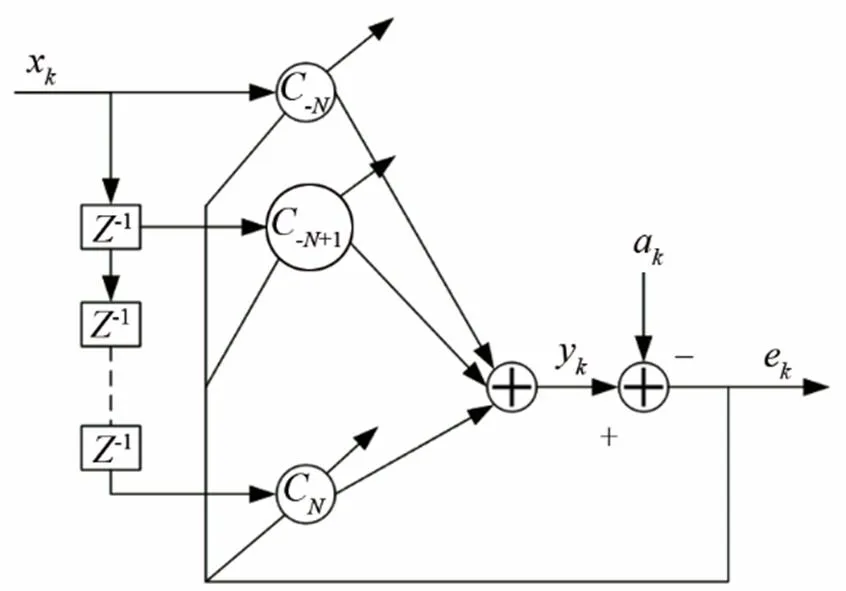
Fig.1 Schematic diagram of adaptive filter

The adaptive convergence of weights in traditional Least Mean Square (LMS) algorithm is slow in sparse multipath channels, where a large number of sequences are required, and the utilization rate of frequency band is not ideal[8].However, impulse response energy of sparse multipath channel is mainly concentrated on several taps with large spacing between each other, and the most of tap energies are tending to zero, so the weights of the equalizer in sparse multipath channel are sparse, and the training process of adaptive equalizer can be regarded as the weighted sum of sparse signals to the dictionary in Compressed Sensing (CS) theory. Many engineering problems involve the process of solving sparse signals, but the CS theory needs to satisfy two necessary conditions: The original signals are sparse in a transform domain and the observation matrix satisfies finite isometric property[9]. CS can reconstruct potential sparse signals from actual observations by solving optimization problems, and the sparse domain is used to restore the original signals, therefore, it has a wide range of applications in medical, communication, imaging and other scientific fields.

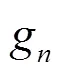
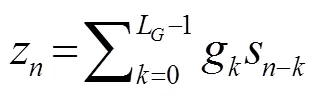
Thus, it can be concluded that:

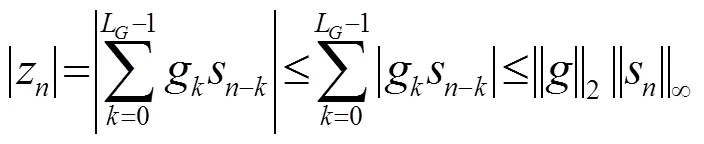
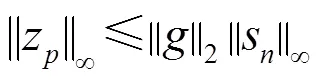
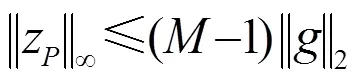
The above equation indicates that under a suitable assumption, the inequality (8) can be written as an equality, given that the transmitting sequence is sufficiently rich in the sense.

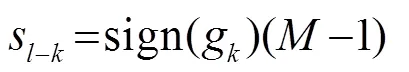
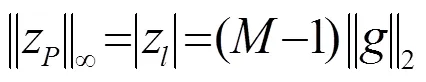
2 Compression sensing adaptive equalization settings

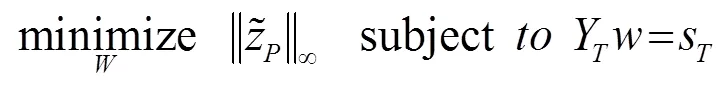
and similarly Noisy-Setting-III can be adapted to the QAM case as Noiseless-Setting-Ⅲ-QAM:

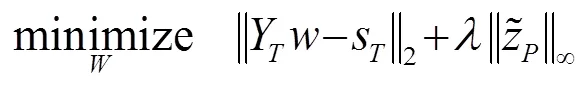
The reason behind this slight modification of theQAM case can be explained by the following equation:

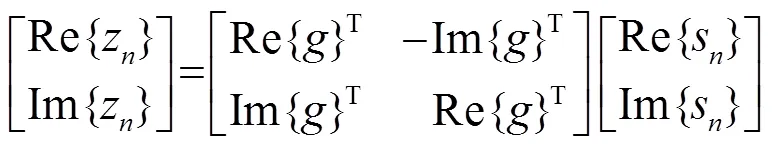
Consequently,

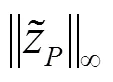
(2) Real equalizer output peaks:

(3) Imag equalizer output peaks:

(4) 2- norm gradient:Ⅲ

(6) Update vector:

(7) Nesterov step:

(8) Normalization:

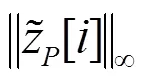
The CoTA algorithm can be used to realize the flexible structure of decision guidance pattern. After the initial iteration, the algorithm can continuously extend the training region by appending the reliable decisions. In the following part, the compressed sensing adaptive equalization without noise is analyzed to judge the impact of training sequence on the results.

2.1 Noiseless case

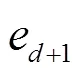
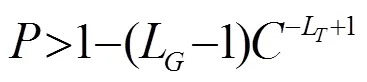
Whereis 4 for QAM and 2 for PAM constellations. Equation (16) is also true for general PAM and QAM constellations. Equation (16) illustrates the phase transition result for the sparse reconstruction problem in compressed sensing as it arises as the equivalent problem to original adaptive equalization problem in noiseless setting.

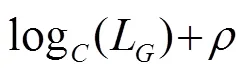
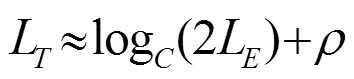
According to the number of equalizer coefficients, for channel propagation:

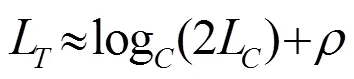
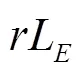
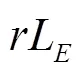
2.2 Noisy case

When SNR is relatively low, the following two performance indicators need to be considered.

ISI level:

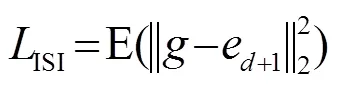
Mean square error:

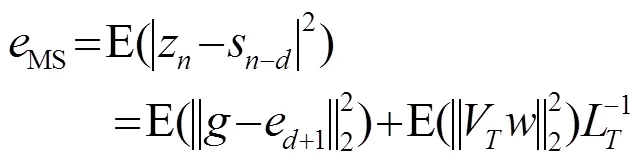
Where, the second term on the right hand side of (15) represents the filtered noise power at the output of the equalizer.

3 Adaptive single-carrier frequency- domain equalization

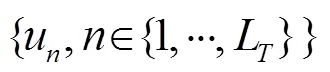
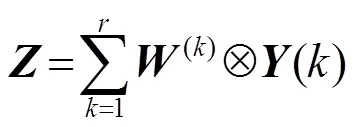
In the adaptive setting, the scenario where the equalizer is trained by using a single block is considered. This is a desired performance for the adaptive algorithm which gives the channel coherence time constraints mandated by wireless mobile environments. The compressed training approach is a good fit for this task, where the goal is to increase the room for the data symbols by restricting the amount of training symbols in the same block (the presented approach can be easily extended to multi-block-based training). For the adaptive compressed training-based SC-FDE, the following optimization setting is designed:

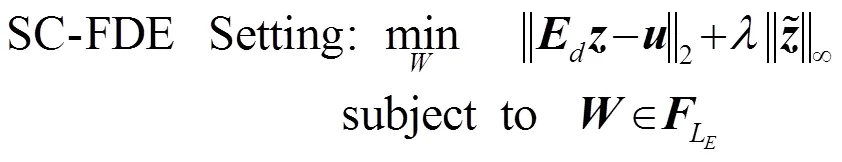
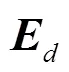
4 Simulation experiment and analysis

In order to verify the performance of the proposed compressed training based adaptive algorithm, the traditional LMS adaptive equalization algorithm is compared. The contrast experiments are conducted in the cases with noise and without noise to show the superiority of compressed training based adaptive algorithm.

4.1 Noisy case

In this case, the input signal is set as

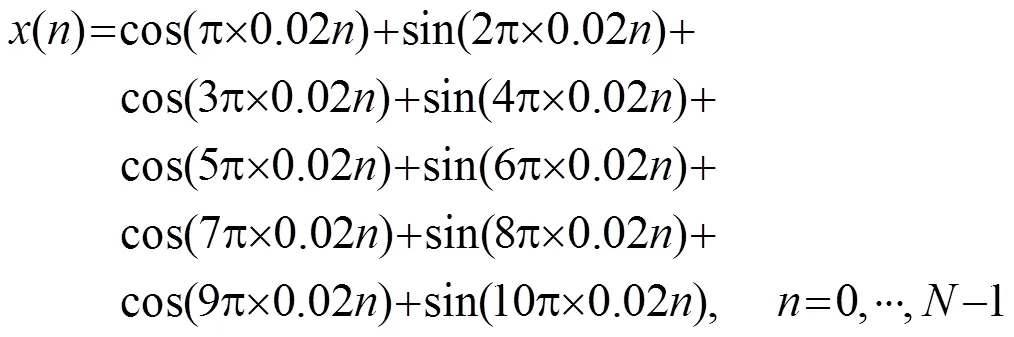
and Gaussian noise with a variance of 0.5 is added to conduct experiments of two different algorithms respectively, in which the number of fixed taps of the compressed training based adaptive algorithm is 5. The experimental results are shown in Fig.2.

From Fig.2(a), it can be seen that the fitting of the actual signal and prediction signal output by the traditional LMS adaptive equalization algorithm is not very ideal and the rate of convergence is slow. The fitting has not converged at the 500thstep of iteration, and even the fluctuation is relatively large, which is mainly caused by the insufficient training sequence. Compared with the traditional LMS adaptive equalization algorithm, the compressed training based adap- tive algorithm in Fig.2 (b) has an ideal fitting with the prediction signal and basically converges in about 150 stepsof iteration. Its convergence speed is obviously much faster than that of the traditional LMS algorithm.

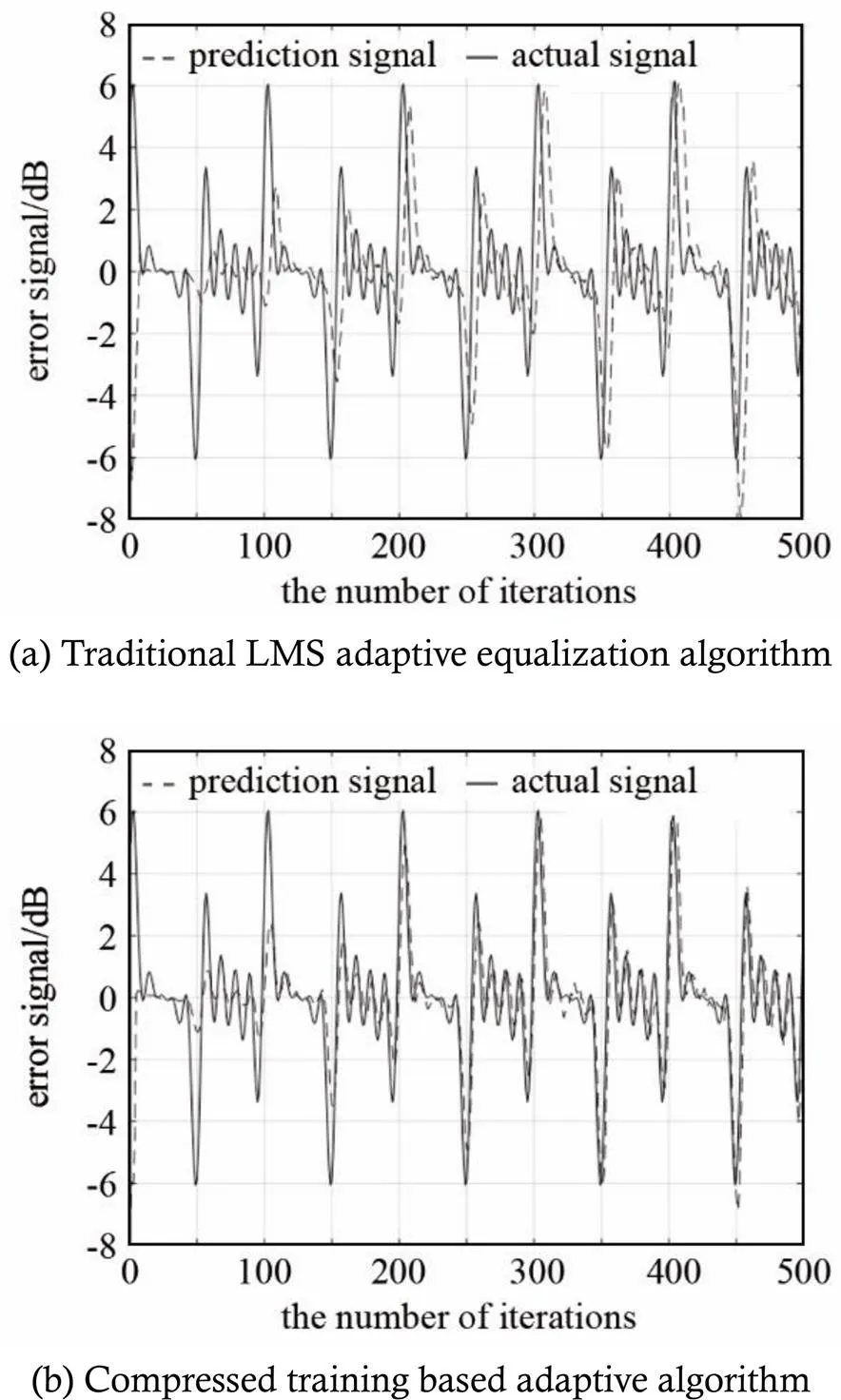
Fig.2 Experimental results of adaptive equalization with noise

4.2 Noiseless case

The above signals are still used in this experiment, except that there is no noise added in this case. The experiment results of two different algorithms are shown in Fig.3.

Similar to the results of the experiment 4.1, the convergence speed of the compressed training based adaptive algorithm is much faster than that of the traditional LMS algorithm. The fitting shown in Fig.3(a) does not converge well even at the 500thstep of iteration, while the fitting shown in Fig.3(b) is basically stable at the 150thstep of iteration.

Therefore, whether there is noise or not, the performance of the CoTA algorithm is better than that of traditional LMS algorithms.

4.3 Comparison with BP algorithm

Fig.3 Experimental results of adaptive equalization without noise

Table 1 Complexity comparison

The simulation experiments of the BP algorithm in the cases of the first 500 sample points with and without noise are conducted, and the results are shown in Fig.4, from which it can be seen that no matter whether there is noise or no noise, a large error exists between the actual output signal and the ideal output signal after the 500thstep of iteration. Especially, when the signal changes rapidly, the error is more serious. which indicates that the convergence accuracy of the BP algorithm is not high and the convergence effect is not very good even at the 500thstep of iteration due to the existance of relatively large fluctuation, which is mainly caused by insufficient training sequences. For the BP algorithm, at least 400 iterations are needed to gradually reach a convergence state, where the actual output signal and the ideal output signal are basically fitted, and the error vector amplitude EVM of the error signal obtained by the simulation is 0.113 2. Such a fitting result is not ideal for modeling in practical application.

Fig.4 Experimental results of adaptive equalization with/without noise by BP algorithm

Compared with the experimental results for CoTA algorithm in Fig.2, it can obviously be found that the convergence speed of CoTA algorithm is faster than that of BP algorithm. By the CoTA algorithm, only 90 iterations are required to achieve a better fitting and reasonable output signal. The error vector amplitude EVM of the output signal obtained by the simulation is 0.006 8, which is two orders of magnitude smaller than the EVM obtained by BP algorithm.

5 Conclusion

[1] VLACHOS E, LALOS A S, BERBERIDIS K. Stochastic gradient pursuit for adaptive equalization of sparse multipath channels[J]. IEEE Journal on Emerging & Selected Topics in Circuits & Systems, 2012, 2(3): 413-423.

[2] ZHANG K, HONGYI Y U, YUNPENG H U, et al. Reduced constellation equalization algorithm for sparse multipath channels based on sparse bayesian learning[J]. Journal of Electronics & Information Technology, 2016.

[3] 周孟琳, 陈阳, 马正华. 一种适用于稀疏多径信道的自适应均衡算法[J]. 电讯技术, 2019, 59(3): 266-270.

ZHOU Menglin, CHEN Yang, Ma Zhenghua. An adaptive equalization algorithm for sparse multipath channels[J]. Telecommunications technology, 2019, 59(3): 266-270.

[4] YILMAZ B B, ERDOGAN A T. Compressed training adaptive equalization[C]//In Proc. IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP’ 16). IEEE, Mar. 2016: 4920-4924.

[5] OYMAK S. “Convex relaxation for low-dimensional representation: Phase transitions and limitations,” Ph.D. dissertation, California Institute of Technology, Jun. 2015.

[6] 宫改云, 姚文斌, 潘翔. 被动时反与自适应均衡相联合的水声通信研究[J]. 声学技术, 2010, 29(2): 129-134.

GONG Gaiyun, YAO Wenbin, PAN Xiang. Research on underwater acoustic communication combined with passive time-inverse and adaptive equalization[J]. Technical Acoustic, 2010, 29(2): 129-134.

[7] JIAO J, ZHENG X J . Extended sparse multipath channel capacity estimation based on adaptive array configuration[J]. Advanced Materials Research, 2013(765-767): 2728-2731

[8] Al-Awami A T, Azzedine Zerguine, Lahouari Cheded, et al. A new modified particle swarm optimization algorithm for adaptive equalization[J]. Digital Signal Processing, 2011, 21(2): 195-207.

[9] DONOHO D L. Compressed sensing, IEEE Transactions on Information Theory, 2006, 52(4), 1289-1306.

[10] 马思扬, 王彬, 彭华. l_0-范数约束的稀疏多径信道分数间隔双模式盲均衡算法[J]. 电子学报, 2017, 45(9): 2302-2307.

MA Siyang, WANG Bin, PENG Hua. Sparse multipath channel fractional interval blind equalization algorithm with l_0-norm constraint [J]. Acta electronica sinica, 2017, 45(9): 2302-2307.

[11] CEVHER V, BECKER S, SCHMIDT M. Convex optimization for big data: Scalable, randomized, and parallel algorithms for big data analytics[J]. IEEE Signal Processing Magazine, 2014, 31(5): 32-43.

[12] 马丽萍. 多模盲均衡算法的稳态性能研究[D]. 大连: 大连海事大学, 2018.

MA Liping. Research on steady-state performance of multi-mode blind equalization algorithm[D]. Dalian: Dalian maritime university, 2018.

稀疏多径信道自适应均衡算法研究

李文艳，朱婷婷，王琪

(西安工业大学电子信息工程学院，陕西西安 710021)

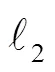
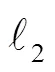
TN911

A

1000-3630(2019)-06-0698-07

10.16300/j.cnki.1000-3630.2019.06.017

2019-07-08;

2019-10-10

Fund: Shaanxi province science and technology key research and development program general projects (2019GY-084)

Author: LI Wenyan (1994－), female, was born in Baoji, Shaanxi province, China. She received the master's degree. Her research fields is information transmission and processing.

LI Wenyan, E-mail: 2963454019@qq.com