利用空间填充曲线和灰度分布估计的声图分割
2020-01-19杨海东孙正凯
杨海东,孙正凯
利用空间填充曲线和灰度分布估计的声图分割
杨海东,孙正凯
(南昌理工学院,江西南昌 330044)
针对声图中的目标分割问题,提出了一种利用空间填充曲线和灰度分布估计的声图目标分割方法。该方法首先利用空间填充曲线将声图由二维矩阵变换为一维向量;其次在一维空间下进行滤波、灰度分布估计、阈值计算、分割处理;最后将分割后的一维向量逆变换为二维矩阵,得到目标分割结果。实际的声图处理验证了方法的有效性。
声图目标分割;空间填充曲线;灰度分布估计
0 引言
成像声呐是探索海底最主要的手段之一,对声图中各类目标的分割及识别是声呐图像处理的主要内容[1-3]。多数声图为二维图像,其后处理也在二维框架下进行[4]。与一维处理相比,二维处理的运算量较大,较难满足实时处理以及需要快速后处理时的需求。因此,如果对二维声图进行降维,并研究在一维情形下的信号处理方法,可极大提高声图后处理的效率,使实时处理和快速后处理易于实现。
空间填充曲线能够将多维空间数据映射为一条曲线,从分形角度看这条曲线的维数仍然为原空间数据的维数,但在数据角度上看其为一维向量[5-6]。对空间填充曲线贡献最大的是数学家康托、皮亚诺和希尔伯特,前者提出了一维到二维的映射理论,后两人则提出了这种映射曲线的做法,他们所发现的曲线分别被称为皮亚诺曲线或希尔伯特曲线[7]。
常见的声呐图像灰度分布模型有威布尔分布、瑞利分布、高斯分布,以及升级的混合分布等模型[8]。其中威布尔分布比瑞利分布能够更好地逼近声呐图像的灰度分布曲线,瑞利分布具有运算效率高的特点。
本文在综合分析典型的空间填充曲线和灰度分布估计的基础上,首先,利用空间填充曲线将声呐图像由二维矩阵变换为一维向量。其次,利用灰度分布估计,计算分布参数,并由此计算声呐图像的目标分割阈值。再次,在声图一维向量基础上进行滤波降噪处理,利用阈值分割目标及阴影。最后,利用空间填充曲线的逆变换将目标所在区域分割出来。
1 任意矩形空间填充曲线
空间填充曲线,顾名思义即指能够将空间填满的一条曲线,其严格的数学定义是:一个维空间填充曲线是一个连续的满射,将单位区间[0, 1]映射到维超立方空间[0, 1]。空间填充曲线有很多种,目前主要有Peano曲线、希尔伯特曲线、Moore曲线、Morton曲线(Z曲线)等。
空间填充曲线将二维图像降为一维向量后,势必会改变原二维图像上像素间的空间位置关系,重点是各像素与其二维邻域空间其他各像素的关系。不同的填充曲线对原有像素间空间关系的保留能力不同,这种能力称为填充曲线的“聚集特性”(clustering properties)。众多空间填充曲线中,数据聚集特性优异且应用广泛的是由希尔伯特在1891年发现的希尔伯特曲线。文献[9]严格证明了希尔伯特曲线在二维空间中比Z曲线拥有更好的聚集特性,并通过仿真表明在二维和三维空间中,希尔伯特曲线的聚集特性优于Z曲线和Gray编码曲线。
1.1 希尔伯特曲线的基本形式及生成方法
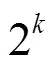
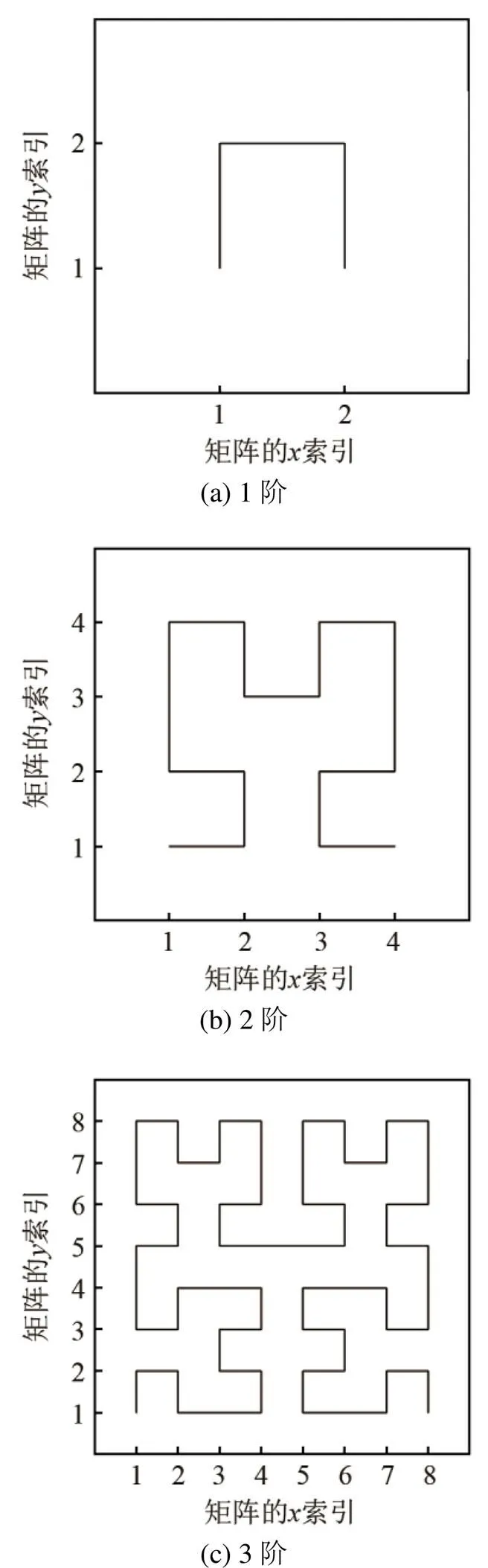
图1 1~3阶希尔伯特曲线

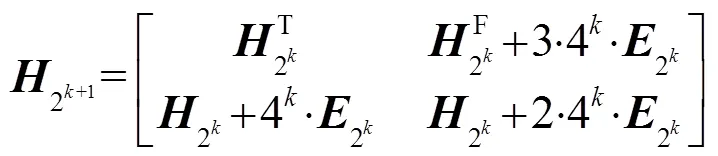
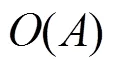

图2 希尔伯特扫描曲线的四种方向
1.2 任意边长正方形的空间填充曲线
设正方形边长为,则可以表示为
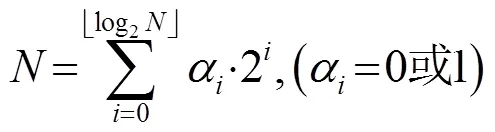
构造扫描矩阵的步骤如下:
设希尔伯特扫描矩阵的起点在左上角,扫描矩阵分层示意图如图3所示。
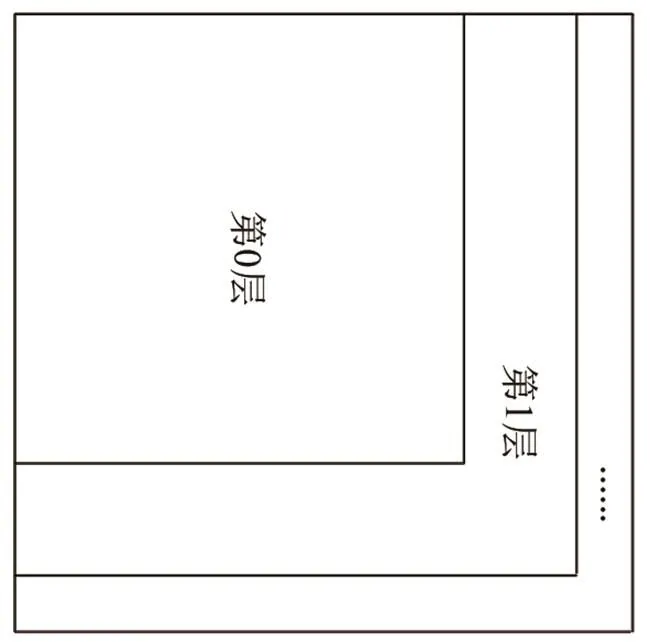
图3 任意边长正方形的希尔伯特扫描矩阵分层示意图
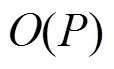

图4 希尔伯特扫描矩阵层的扫描方向
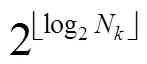
1.3 任意矩形的空间填充曲线
对于任意矩形,其空间填充曲线可由若干个基于正方形的空间填充曲线首尾连接组成。其基本思路是将在矩形中分割出最大的正方形,对其提取任意边长正方形的空间填充曲线,在剩余的矩形中继续执行该操作,直至剩余部分为空。
设矩形的行数和列数(即矩阵的长和宽)分别为和,计算任意矩形的空间填充曲线扫描矩阵的基本步骤如下:
(3) 循环执行上述操作,直至剩余部分为空,将上述矩阵顺次连接后形成扫描矩阵。
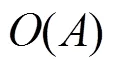
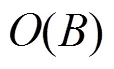
2 声呐图像处理
2.1 降维和滤波处理
声呐图像是水中或水底目标的后向散射强度的体现。一般在内陆河流湖泊、近海港口或渔区的背景较为复杂,在近海其他水域和远海海底背景较为单一、目标较为简单。此外与光学图像相比,声呐图像的分辨率低、噪声较高。因此声呐图像的滤波是目标识别中非常重要的步骤。
首先利用任意矩形空间填充曲线扫描矩阵,将二维声呐图像做降维处理,生成一维向量,如式(3)所示:
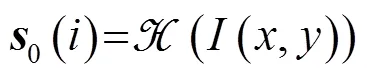
由于声呐图像非直接成像,需要对原始采集数据进行信号处理后才能获得,同时由于声呐分辨率低,水声环境复杂,声呐图像的背景噪声较强。因此在目标分割前对声图进行必要的滤波处理,可提高声呐目标分割的效率和正确率。
对于声图降维后的一维向量,与二维矩阵相比,一些滤波方法的处理效率会得到较大提升。
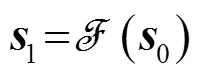
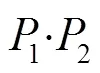
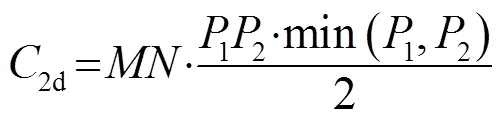
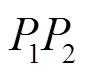
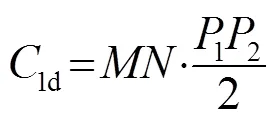
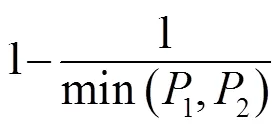
2.2 利用灰度分布估计的目标分割
图像灰度分布估计有很多种模型,典型的如高斯模型、瑞利分布模型、威布尔分布模型,以及升级的混合分布模型等。
根据MIDDLETON提出的海底混响模型[11],成像结果是大量随机相位散射体的叠加(积分),幅度和相位相互独立,并且根据中心极限定理,海底散射混响的幅值服从瑞利分布。瑞利分布是威布尔分布的一种特殊形式,即威布尔分布包含了瑞利分布。大量实验处理结果表明,威布尔分布比瑞利分布更接近声呐图像的灰度分布。当成像区域中有强点目标或散射体较少时,声图灰度分布服从K分布或Gamma分布[12-13]。
实际中大多数成像声呐基于海底混响成像,包括前下视声呐、下视多波束声呐、侧视声呐、侧视合成孔径声呐等。并且海底声图中强点面积一般远小于背景区域,因此威布尔分布适用于大部分声图。威布尔分布的分布函数为

式中,为幅度,为尺度参数,为形状参数。对于图像灰度分布,用来控制概率最大的灰度值所在的位置,用来控制灰度值的集中程度。
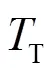
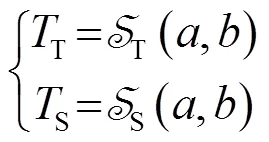
利用威布尔分布参数的阈值分割策略生成目标阈值和阴影阈值,其优点在于可自适应地应用于不同情形下亮度差异较大的图像。
目前主流的图像灰度是位于[0, 225]之间的整数,分析威布尔分布函数,可以看出灰度值与尺度参数近似为正比例关系,与形状参数为指数关系,利用这种关系以及参数和阈值间的定性关系提出目标阈值和阴影阈值的策略函数为
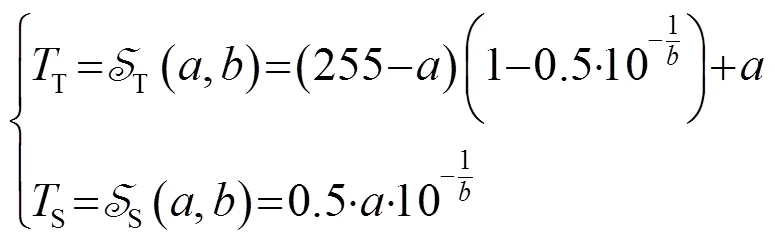
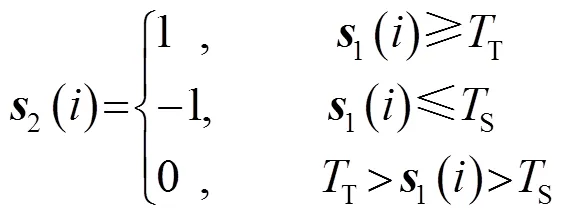
3.3 利用空间填充曲线逆变换为二维目标分割结果
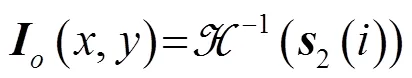
3 实验数据处理
(1) 声呐原图
图5为2幅典型的侧扫声呐图像,图5(a)是由Klein公司的S3900侧扫声呐对遇难者的成像结果[14],图5(b)是S4900型侧扫声呐的成像结果,图中包含了一个水泥台及其上固定的绳缆。

图5 两幅实际的目标声图
(2) 图像进行扫描后的一维向量
对声图利用空间填充曲线矩阵进行扫描,产生一维向量。其中遇难者声图的一维向量如图6(a)所示。作为对照,图6(b)给出了原图按照每行进行扫描后的一维向量曲线。对比可以看出,采用填充曲线矩阵扫描后的一维向量,图中幅度较高处(即声图中的目标部分)较为集中,而采用按行扫描的图像其幅度较高的部分较为分散。
图7是对“绳缆”声图进行空间填充曲线扫描7(a)和逐行扫描7(b)的结果。在本实例中,由于原图总体亮度水平较高,因此在图中灰度值较大处较多,但仍可以从两个结果的对比看出,空间填充曲线扫描结果的集中度更高。
通过对两幅声图分别采用空间填充曲线扫描向量和逐行扫描向量产生的一维向量进行定性分析,可以看出经空间填充曲线扫描向量处理的结果,其目标集中度更好,更有利于后续滤波处理。
(3) 一维向量滤波处理
获得声图一维向量后,即可进行一维滤波处理,在一维向量上进行处理比二维图像域处理速度更快。
图8是遇难者声图对应一维向量的平滑滤波、中值滤波等处理结果的局部。从图8中可以看出,幅度较大部分的中值滤波效果更好。
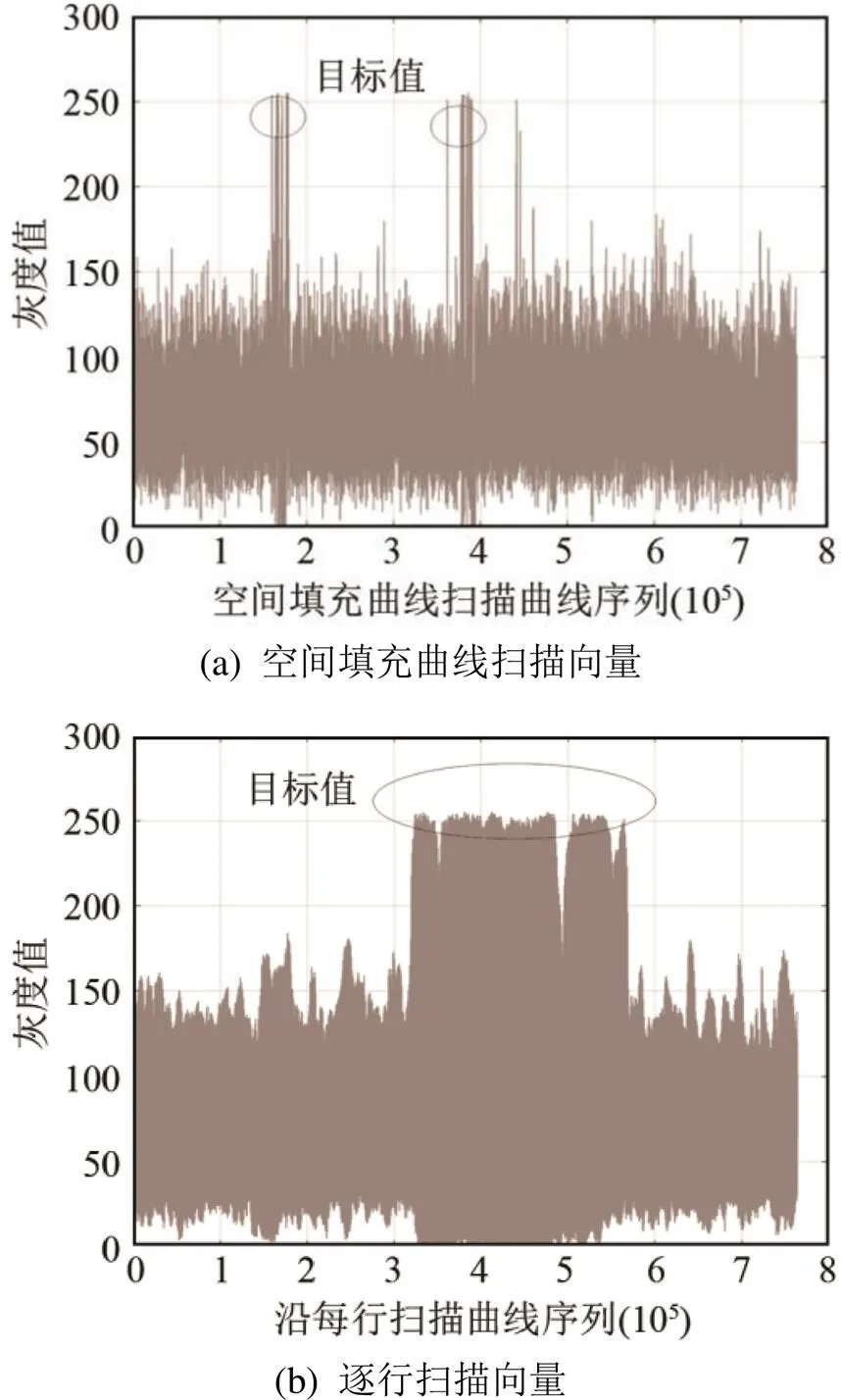
图6 “遇难者”声图扫描向量

图7 “绳缆”声图扫描向量
(4) 威布尔分布估计及阈值计算
对一维向量进行威布尔分布估计,原图灰度直方图分布及威布尔分布曲线如图9所示。
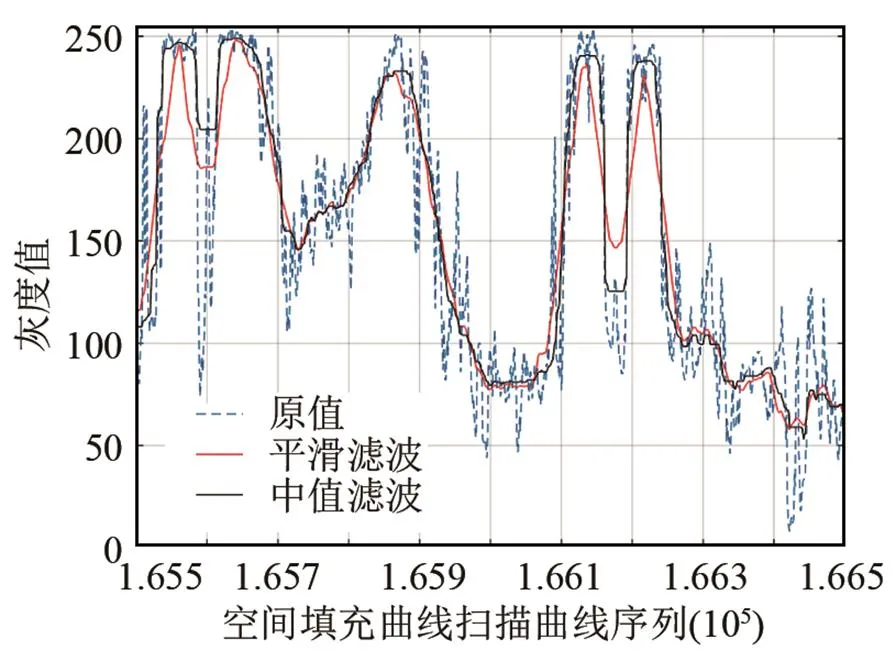
图8 声图扫描向量的滤波
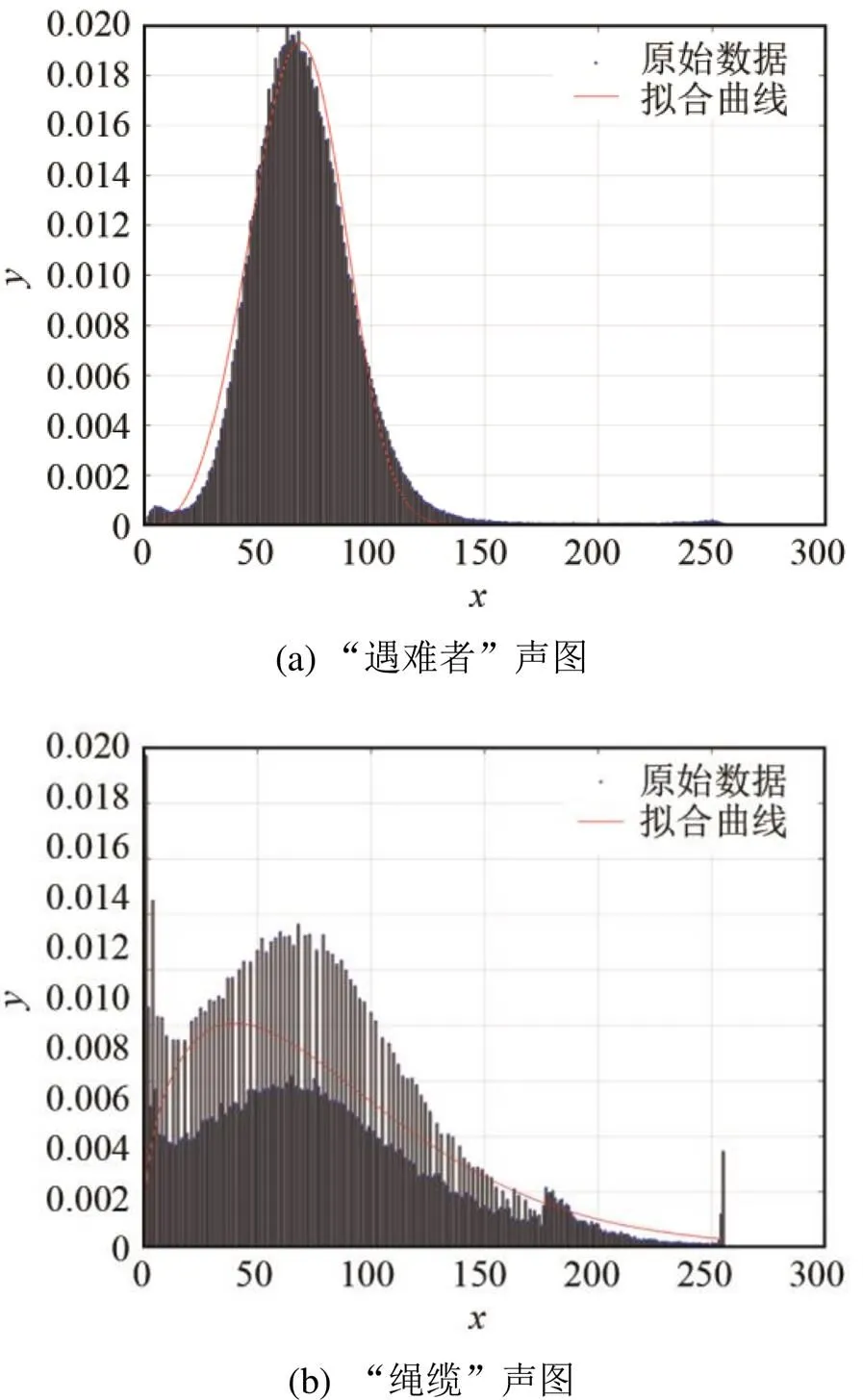
图9 两个目标声图的灰度分布直方图及威布尔分布曲线
利用分布参数计算目标阈值和阴影阈值如表1所示。
(5) 利用阈值的目标分割和阴影分割
针对本文中所使用的图像和计算的目标阈值和阴影阈值,对两幅图像进行分割处理,作为对照,给出在二维图像域上进行分割的其他两种方法,即直接阈值分割、二维中值滤波后分割。

表1 威布尔分布估计参数及阈值
本文空间填充曲线及灰度分布估计(Space Filling Curve and Grayscale Distribution Estimation, SFP-GDE)方法针对直接阈值分割的优点在于其较高的准确率,而针对二维中值滤波后阈值分割方法的优点,在于其运算效率的提高。为此统计上述不同方法针对两幅声图处理时的准确率、运算时间,进行定量比较分析。
利用人工识别在遇难者声图和绳缆声图中使用一个矩形将目标和阴影所在区域选中,区域外的像素点识别为目标或阴影的判定为错误识别,区域内则不计入统计。两幅声图目标区人工选择示意如图10所示。

图10 人工划分目标区
3种方法的分割结果如图11所示。图11中白色部分为分割出的目标部分,灰色部分为分割出的背景部分,黑色部分为分割出的阴影部分。
3种方法的误分率统计和处理时间如表2和表3所示。
通过对分割结果的对比可以看出,采用本文提出的SFP-GDE方法,其误分率与声图在二维域上进行滤波后再进行阈值分割相当,但处理时间则远小于后者,这是因为中值滤波在二维域处理和一维域处理的差异导致。

图11 不同方法的目标声图分割结果:左,本文SFP-GDE 方法;中,二维中值滤波后阈值分割;右,直接阈值分割
与直接阈值分割相比,本文虽然在运算时间上不占优势,但误分率则明显小于直接阈值分割法。
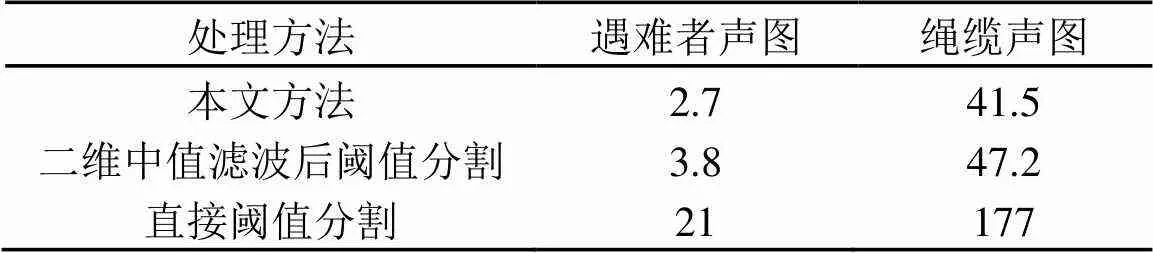
表2 误分率统计结果(10-4)
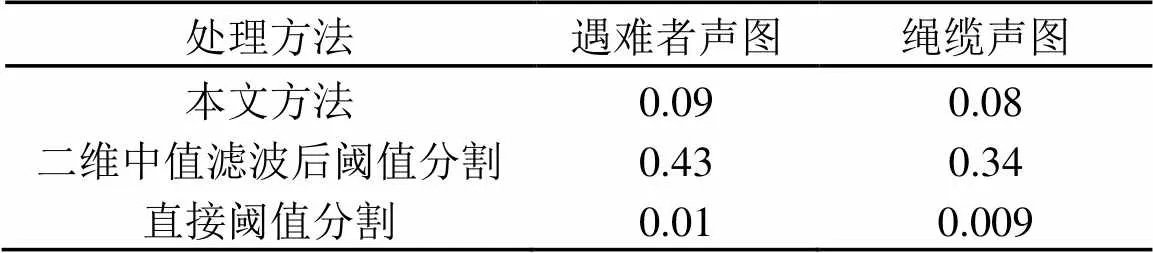
表3 处理时间统计结果(s)
4 结论
声图目标分割是声图处理的一个重要方向,本文提出了利用空间填充曲线扫描矩阵来将声呐图像由二维矩阵变换为一维向量。并在一维空间下进行滤波处理,之后利用灰度分布估计参数获得目标分割和阴影分割的阈值,并将一维向量的元素划分为目标、背景、目标阴影3类。最后将分类后的向量逆变换为二维矩阵,即获得了声图目标的分割结果。本方法的优点主要在于声呐图像的滤波阶段,经降维后可极大降低运算量。利用对实际声图的处理结果,验证了提出方法的有效性。
此外,仍有一些方法在一维域上进行阈值检测比二维域上的检测要更为便利,例如局部峰值检测等。在局部峰值检测后再变换至二维域进行形态学腐蚀也可得到有益的成果。
致 谢 本文中所使用的声呐图像来自于Klein公司网站,该图像是Klein S3900侧扫声呐对假人获得的高清成像结果,在此对Klein公司表示感谢。
[1] MIGNOTTE M, COLLET C, PEREZ P, et al. Sonar image segmentation using an unsupervised hierarchical MRF model[J]. IEEE Trans. Image Process, 2000, 9(7): 1216-1231
[2] 卢逢春, 张殿伦, 郭海涛. 基于属性直方图的图像分割方法及其在声呐图像分割中的应用[J]. 哈尔滨工程大学学报, 2002 , 23(3): 1-3.
LU Fengchun, ZHANG Dianlun, GUO Haitao. Image segmentation based upon bounded histogram and its application to sonar image segmentation[J]. Journal of Harbin Engineering University, 2002, 23(3): 1-3.
[3] 霍冠英, 刘静, 李庆武, 等. 空间约束FCM与MRF结合的侧扫声呐图像分割算法[J]. 仪器仪表学报, 2017, 38(1): 226-235.
HUO Guanying, LIU Jing, LI Qingwu, et al. Side-scan sonar image segmentation algorithm based on space-constrained FCM and MRF [J]. Chinese Journal of Scientific Instrument, 2017, 38(1): 226-235
[4] 姜枫, 顾庆, 郝慧珍, 等. 基于内容的图像分割方法综述[J]. 软件学报, 2017, 28(1): 160-183.
JIANG Feng, GU Qing, HAO Huizhen, et al. Survey on content-based image segmentation methods[J]. Journal of Software, 2017, 28(1): 160-183.
[5] 刘树群, 耿德磊. 二维空间填充曲线的生成方法[J]. 甘肃科学学报, 2010, 22(3): 105-107.
LIU Shuqun, GENG Delei. The generation method of 2D space-filling curves[J]. Journal of Gansu Sciences, 2010, 22(3): 105-107.
[6] 曹奎, 冯玉才. 基于GM模型和Hilbert空间填充曲线的图象压缩方法[J]. 小型微型计算机系统, 2002, 23(11) :1359-1362.
CAO Kui, FENG Yucai. An image compression method based on GM and Hilbert space filling curve[J]. Journal of Chinese Computer System, 2002, 23(11): 1359-1362.
[7] 王笋, 徐小双. Hilbert曲线扫描矩阵的生成算法及其MATLAB程序代码[J]. 中国图象图形学报, 2006, 11(1): 119-122.
WANG Sun, XU Xiaoshuang. A new algorithm of Hilbert scanning matrix and its MATLAB program[J]. Journal of Image and Graphics, 2006, 11(1): 119-122.
[8] 翟厚曦, 江泽林, 张鹏飞, 等. 一种合成孔径声呐图像目标分割方法[J]. 仪器仪表学报, 2016, 37(4): 887-894.
ZHAI Houxi, JIANG Zelin, ZHANG Pengfei, et al. Object segmentation method for synthetic aperture sonar images[J]. Chinese Journal of Scientific Instrument, 2016, 37(4): 887-894.
[9] BONGKI M, JAGADISH H V, FALOUTSOS C. Analysis of the clustering properties of the Hilbert space filling curve[J]. IEEE Trans. Knowl. Data Eng., 2001, 13(1): 124-141.
[10] CHUNG K L, HUANG Y L, LIU Y W. Efficient algorithms for coding Hilbert curve of arbitrary sized image and application to window query[J]. Information Sciences, 2007, 177(10): 2130-2151.
[11] MIDDLETON D. A statistical theory of reverberation and similar first-order scattered fields[J]. IEEE Transactions On Information Theory, 1967, 13(3): 372-392.
[12] GENSANE M. A statistical study of acoustic signals backscattered from the sea bottom[J]. IEEE J. Oceanic Eng., 1989, 14(1): 84-93.
[13] 霍冠英, 刘静, 李庆武. 侧扫声呐图像统计特性研究[J]. 传感器与微系统, 2017, 36(3): 25-28 HUO Guanying, LIU Jing, LI Qingwu. Study of statistical characteristics of side scan sonar image[J]. Transducer and Microsystem Technologies, 2017, 36(3): 25-28.
[14] System 3900 Digital Side Scan Sonar [EB/OL]. http://kleinmarinesystems.com/products/side-scan-sonar/system-3900/.
Research on sonar image segmentation by spatial filling curve and grayscale distribution estimation
YANG Hai-dong, SUN Zheng-kai
(Nanchang Institute of Technology, Nanchang 330044, Jiangxi, China)
Aiming at the problem of target segmentation in sonar images, a method based on space filling curve and grayscale distribution estimation is proposed and named as SFC-GDE Method. In this method, the space filling curve is firstly used to transform sonar image from two-dimension matrix to one-dimension vector, and then, the entire sonar image processing process, including filtering, grayscale distribution estimation, threshold calculation and image segmentation, are carried out in one dimensional space. Finally, the segmented one-dimensional vector is transformed into a two-dimensional matrix by inverse transformation to achieve target segmentation. Actual sonar image has been processed to verify the effectiveness of the proposed method.
sonar image object segmentation; space filling curve; grayscale distribution estimation
TP751
A
1000-3630(2019)-06-0691-07
10.16300/j.cnki.1000-3630.2019.06.016
2018-08-12;
2019-03-02
江西省教育厅2017年度科学技术基金重点项目(GJJ171041)
杨海东(1983-), 男, 山西长治人, 硕士, 讲师, 研究方向为电子信息科学与技术,软件工程。
杨海东, E-mail: yanghaidong_nit@sina.com
