基于数学实验下类切线方程的探讨
2020-01-18张硕
张硕

[摘 要] 圆锥曲线的切线问题,在高考中是一大亮点,一些文献中均有不同方面的探究. 文章主要探究一类形似切线方程,同时借助数学实验探讨该类直线与圆锥曲线的位置关系,根据定点选择的不同,进一步论证了该类切线与圆锥曲线的交点个数,探讨了该知识点的具体几何意义.
[关键词] 圆锥曲线;椭圆;双曲线;抛物线;切线;位置关系
高考中常遇到一些形似于圆锥曲线切线方程的直线问题,这些直线看似切线形式,但由于定点的选择不同,这些直线也将会有自己的实际意义.笔者发现2019年全国Ⅲ卷,2014年广东卷,2013年安徽卷、山东卷、广东卷等均对该知识点做了不同层面的考查和应用.
引理:设P(x■,y■)为圆锥曲线Ax2+By2+Cx+Dy+F=0上一点,则该圆锥曲线过点P的切线方程为:Ax■x+By■y+C■+D■+F=0.
简析:引理的常用证明有,方法1:判别式法,直线代入圆锥曲线;方法2:高等数学方法,隐函数求导,此处详细证明略,主要领会圆锥曲线的一般切线形式和方程思想即可.本文中把形如引理中切线方程的直线,称之为“类切线”.
■提出问题
探究如下问题:已知椭圆方程■+y2=1,定点P■(x■,y■),直线方程为■+yy■=1.
(1)当■+y■=1,则直线■+yy■=1与椭圆■+y2=1的交点个数______.
(2)当■+y■>1,则直线■+yy■=1与椭圆■+y2=1的交点个数______.
(3)当0<■+y■<1,则直线■+yy■=1与椭圆■+y2=1的交点个数______.
■实验探究
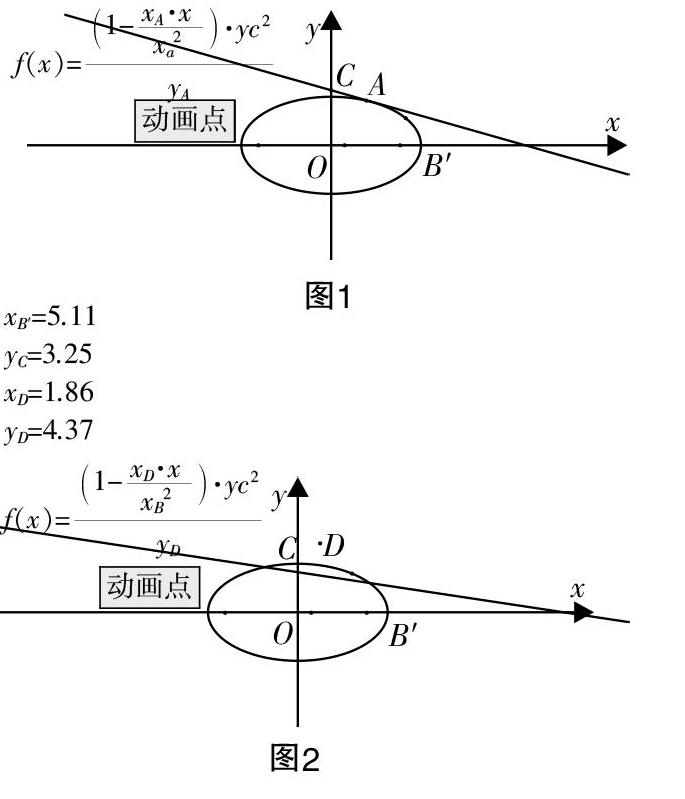
借助数学软件几何画板对不同的数学实验进行探究,即取不同的点P■(x■,y■)使其分别满足上式的条件,通过实验发现(1)式直线即为该椭圆的切线,与椭圆交点个数为一个;(2)式直线与该椭圆相交,交点个数为两个;(3)式直线与该椭圆相离,交点个数为零个. 实验如图1、2、3所示.
通过上面一个具体的例子,我们可以进一步探究,根据定点P■(x■,y■)的三个不同位置,所确定的直线对于一般的椭圆曲线具有不同的几何意义,它们的位置关系也不一样.
■理论证明
由以上实验的探究,可以进一步给出理论上的证明:
椭圆■+■=1(a>b>0) ,定点P■(x■,y■),直线■+■=1,
■+■=1,■+■=1?圯(a2y■+b2x■)x2-2a2b2x■x+a4b2-a4y■=0.
当y■=0时,直线方程可变为■-1=0;
当y■≠0时,Δ=4a4b4x■-4(a2y■+b2x■)·(a4b2-a4y■)=4a6b2y■■+■-1.
(1)当■+■=1,即点P■(x■,y■)在椭圆上时,所以Δ=4a6b2y■■+■-1=0,故直线■+■=1与椭圆■+■=1(a>b>0)相切,有唯一公共点,即为椭圆的切线方程.
(2)当■+■>1,即点P■(x■,y■)在椭圆外时,当y■≠0时,Δ=4a6b2y■■+■-1>0,当y■=0时,■-1=0顯然与椭圆有两个交点,故直线(类切线)■+■=1与椭圆相交,有两个公共点. 事实上过点P■作椭圆的两切线,该类切线即为过两切点的切点弦所在的直线(证明略).
(3)当0<■+■<1,即P■(x■,y■)在椭圆内部且不与原点重合时,当y■≠0时,所以Δ=4a6b2y■■+■-1<0,当y■=0时,■-1=0显然与椭圆无交点,故(类切线)直线■+■=1与椭圆■+■=1(a>b>0)无公共点.事实上过点P■任作一条直线交椭圆于P■,P■两点,过P■,P■分别作椭圆的切线,该两切线交点的轨迹即为该类切线(证明略).
■探源与类比推广
类比思维是数学核心素养逻辑推理中的分支,通过类比可以发现其中的精髓,因此由椭圆中类切线的实验探究及理论证明,容易类比推广到其他的圆锥曲线上,实验和理论都再次证明(限于篇幅,这里略去实验步骤和实验结果图)这样的类比推广是正确的.
(1)抛物线:x2=2py(p>0),定点P■(x■,y■),直线xx■=p(y+y■),
xx■=p(y+y■),x2=2py ?圯py2+2(py■-x■)y+py■=0,Δ=4x■(x■-2py■).
①当x■=2py■,即P■(x■,y■)在抛物线上时,Δ=4x■(x■-2py■)=0,故直线xx■=p(y+y■)与抛物线x2=2py(p>0)相切,有唯一公共点,即为抛物线的切线方程.
②当x■>2py■,即P■(x■,y■)在抛物线外部时,Δ=4x■(x■-2py■)>0,故直线(类切线)xx■=p(y+y■)与抛物线相交,有两个公共点,几何意义同椭圆.
③当x■<2py■,即P■(x■,y■)在抛物线内部时,Δ=4x■(x■-2py■)<0,故直线xx■=p(y+y■)与抛物线x2=2py(p>0)无公共点,几何意义同椭圆.
(2)双曲线■-■=1(a>0,b>0),定点P■(x■,y■),直线■-■=1,
■-■=1,■-■=1?圯(a2y■-b2x■)x2+2a2b2x■x-a4b2-a4y■=0.
当a2y■-b2x■≠0时,Δ=4a4b4x■+4(a2y■-b2x■)(a4b2+a4y■)=-4a6b2y■■-■-1.
①当■-■=1,即P■(x■,y■)在双曲线上时,Δ=-4a6b2y■■-■-1=0,直线■-■=1与双曲线相切,有唯一公共点,即为双曲线的切线方程.
②当■-■<1,即P■(x■,y■)在双曲线两支之间(不含渐近线上点)时,当y■≠0时,Δ=-4a6b2y■■-■-1>0,直线■-■=1与双曲线相交,有两个公共点,几何意义同椭圆.
③当■-■>1,即P■(x■,y■)在双曲线内部时,当y■≠0时,Δ=-4a6b2y■■-■-1<0,直线■-■=1与双曲线无公共点,几何意义同椭圆.
■真题回顾
由以上理论推导不难发现,2019年全国Ⅲ卷,2014年广东卷,2013年山东卷、广东卷、安徽卷等均对该知识点做了不同层面的考查,体现了高考试题“常考常新,推陈出新”的理念. 这些题均可以用类切线知识的通性通法来解答,由于篇幅关系,此处只做简析.
1. (2019年全国Ⅲ卷)已知曲线C:y=■,D为直线y=-■上的动点,过D作C的两条切线,切点分别为A,B.
(1)证明:直线AB过定点;(2)略.
简析:由上面类切线理论推导知,AB即是所谓的类切线,设Dt,-■,所以直线AB的方程形式:
■=■,即tx-y+■=0,所以直线AB过定点0,■.
2. (2013年山东卷)过点(3,1)作圆(x-1)2+y2=1的两条切线,切点分别为A,B,则直线AB的方程为_______.
简析:由类切线知识,可以直接写出直线AB方程为(x-1)(3-1)+1×y=1,即2x+y-3=0.
3. (2013年广东卷)已知抛物线C的定点为原点,其焦点F(0,c)(c>0)到直线l:x-y-2=0的距离为■. 设P为直线l上的点,过点P作抛物线C的两条切线PA,PB,其中A,B为切点.
(1)略;(2)当点P(x■,y■)为直线l上的定点时,求AB的方程;(3)略.
简析:(2)抛物线C的方程x2=4y,由上面类切线理论推导知,AB即是所谓的类切线,所以可以直接得到直线AB的方程形式:x■x=4×■,
即x■x-2y-2y■=0.
在探究直线与圆锥曲线的位置关系中,类切线方程是极其重要的一部分,近幾年各省市高考均对其有不同的青睐. 本文从实验探究开始,利用理论证明、类比推广等方法,比较系统地探究了根据点的位置选择不同类切线与圆锥曲线的位置关系以及几何意义.
