问题导向驱动能力养成,自主探索落实素养生根
2020-01-18李其龙
李其龙
[摘 要] 文章对平面向量基本定理课堂教学进行反思与重构. 从落实数学素养出发,在教师的问题导向驱动下,让学生进行作图操作,层层深入地探究问题. 让学生从被动接受数学概念转向自主探索数学概念,经历和体验概念的产生和完善过程从而提高数学能力,进而达到数学核心素养落地生根的目的.
[关键词] 课堂教学;问题导向;自主探索;素养生根;反思;重构
■引言
新的教学形势下,如何能够让学生从被动接受数学概念转向自主探索数学概念,经历和体验概念的产生和完善过程从而提高数学能力?如何在课堂教学中体现数学素养的渗透和落实?
下面是笔者以平面向量数量积课堂教学为例,对上述问题进行的反思和重构.
■平面向量基本定理课堂教学的若干反思与思考
1. 关于问题情境的反思和思考
向量具有丰富的实际背景,是重要的数学模型和物理模型. 那么,学习数学模型的最好办法是经历数学建模过程[1]. 但是,很多教师不重视课本上的物理背景引入,或者直接跳过这一环节直奔定理内容,这使得学生错过一个用数学的眼光观察世界的机会,更谈不上提高学生发现和提出问题的能力. 纵观平面向量整章内容,几乎每节内容起始部分都有一个实际的物理背景问题,在例题中也反复出现实际的物理问题,这也在提示我们:在实际教学中,要引导学生对现实原型进行观察,充分发挥现实原型对抽象的数学概念的支撑作用. 所以,引导学生根据生活经验,从火箭升空的速度分解,结合力的分解的平行四边形法则,提出“平面内任一向量是否可以用两个不共线的向量来表示”这一问题,是本节内容最好的问题情境.
2. 关于定理抽象过程的反思与思考
平面向量基本定理是高中数学核心概念之一[2],是把一维的向量共线定理向二维平面的推广,也是后面将要学习的三维空间向量的学习基础,处理得当对向量相关内容的学习和研究有纲举目张的作用.
教师满堂灌式的讲解,学生死记数学概念和机械模仿做题固然也能让学生掌握定理,但是缺少学生参与的课堂是没有灵魂的. 只有让学生真正参与课堂研究,进行自主探索数学概念,经历和体验概念的产生及完善的过程才能提高数学能力,进而达到数学核心素养落地生根的目的.
此前,学生对于向量加减法及数乘运算停留在几何直观上,从几何图形认识到代数符号认识需要一个过程. 通过问题驱动,让学生进行数学探索,通过自己动手做数学,培养学生主动探求知识、合作交流的意识,改善数学学习信念,提高学生学习数学、研究数学的能力. 这也是让学生用数学的思维去分析问题,用数学的语言去表述问题的过程.
基于上述思考,笔者尝试通过对物理现象的几何直观认识出发,层层设问,步步深入,展开对平面向量基本定理的探究,让学生在自主探索过程中体会数学定理的产生,体验定理所蕴含的思想,感受数学思维的形成来落实数学素养.
■平面向量基本定理课堂教学的重构片段实录
片段一:问题情境引入
播放火箭升空短视频,让学生思考两个物理现象和一个数学问题.
两个物理现象:(1)火箭升空的某个时刻,火箭的速度可以分解成豎直向上和水平向前的两个分速度;(2)力的分解,一个力可以运用平行四边形法则分解成两个不共线方向上的力的和.
上面两个现象都是从几何直观上说明,向量可以分解成两个不共线的向量,两个不共线向量可以合成一个向量,这些在向量的加法及向量加法的平行四边形法则中有所体现.
问1:那么代数方面,我们能用数学符号表述上述现象吗?
问2:(数学问题)平面内,任意一个向量能否用两个不共线的向量来表示呢?
我们知道,向量可以用一条有向线段表示,这样,我们既可以从形的角度研究向量,又可以从数的方面研究向量.
请大家在坐标纸上画一个向量a,再作出a乘2和-2所得的向量c和d.
(1)学生在平面上任意画一个向量a,再作出a乘一个数所得的向量.
(2)任意画出一个与a不共线的向量b.
学生动手作图并在教师的引导下复习向量共线定理.
问3:实数m乘非零向量a可以得到与a共线的所有向量吗?
生:可以.
问4:能用数学语言描述这一过程吗?
学生叙述向量共线定理,教师板书.
问5:向量b是否可以用向量a表示?
生:不可以.
片段二:学生动手探索,通过做数学来体验定理的产生过程
师:我们先研究下面的若干问题,首先在复习引入的作图基础上完成下面任务.
作图:
(1)2a+b; (2)-2a+b;
(3)2a-b; (4)-2a-b.
问6:上述问题推广到一般,ma+nb合成的向量唯一吗?
问7:若通过取m和n的不同值,ma+nb可以合成平面内任何一个向量吗?
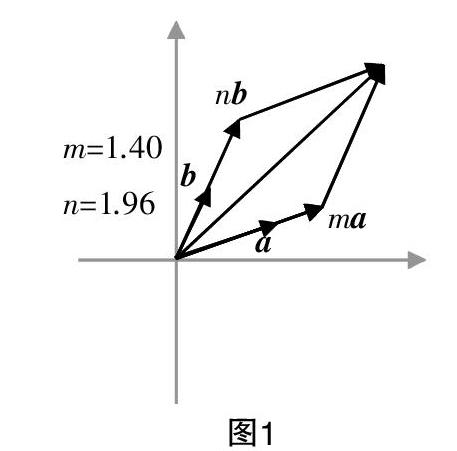
教师用几何画板软件演示向量ma+nb的合成(如图1),并让学生自己通过拖动改变m,n的值观察向量合成的追踪痕迹.
探索结果一:通过取m和n的不同值,ma+nb可以合成平面内任何一个向量.
问8:逆向思考一下,任何一个向量是否可以分解到向量a和向量b的方向上呢?
通过几何画板的作图演示,学生思考并讨论该问题.
探索结果二:在同一平面内,任意一个向量c都可以分解成两个分别在向量a和向量b方向上的向量.
问9:上述几何现象,用代数符号表示是什么样子?
生:c=λ1a+λ2b.
问10:上式中,a与b的系数λ1,λ2是否唯一?
生:由向量共线定理可知,在a和b方向上分解的向量是唯一的,故系数λ1,λ2是唯一的.
探索结果三:在同一平面内,任意一个向量c都可以分解成两个给定向量a和b方向上的向量,分解是唯一的,用代数符号可以表示为:c=λ1a+λ2b,且λ1,λ2是唯一的一组数.
问11:平面上,任意一个向量c能用任意两个不共线的向量表示出來吗?
请学生分组自行探索:一位学生画出一个向量a和任意两个不共线的向量e1,e2,请组内其他学生进行作图分解. 完成后,进行角色交换,再次进行相关探索.
探究结果四:在同一平面内,任意一个向量a都可以分解成两个不共线的向量e1,e2方向上的向量,分解是唯一的,用代数符号可以表示为:a=λ1e1+λ2e2,且λ1,λ2是唯一的一组数.
问12:两个向量e1,e2为何要求不共线呢?请同学们讨论,并结合前面的探究结果进行总结,回答本课开初提出的问题.
生:(1)向量e1和向量e2都为0时不成立. (2)向量e1和向量e2恰有一个为0时,退化为共线向量基本定理. (3)向量e1和向量e2都不为0时,若λ1=0,λ2=0,λ1e1+λ2e2表示0;若λ1与λ2仅有一个为0,退化为共线向量基本定理;一组(λ1,λ2)唯一确定一个向量c.
探究结果五:同一平面内,任意一个向量可以用两个不共线的向量来表示.
类比向量共线定理的符号表示,上述内容用符号语言表述为:如果e1,e2是同一平面内两个不共线的向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2(平面向量基本定理生成).
■课堂重构后的思考
在重构后的课堂教学中,经历了从物理现象到数学问题,从几何直观到代数抽象. 学生自己动手做数学,选用坐标纸作图,教师通过几何画板动画演示向量ma+nb的合成,学生通过拖动改变m,n的值观察向量合成的追踪痕迹,再到任意的分解. 学生进行观察和自己动手参与计算机操作,从视觉和思维上都受到了冲击. 在问题导向的驱动下,分阶段引导学生从几何直观探索平面内任意向量的分解,在探索结果的基础上用代数符号语言进行表述,再对符号语言进行深入的推敲,直至概念的形成. 在探索过程中体会数学思维形成,体验定理所蕴含的思想,感受数学符号语言的魅力,经历从几何直观到代数抽象的升华. 让学生从被动接受数学概念转向到自主探索数学概念的生成. 学生从经历和体验概念的产生及完善的过程中提高数学能力,进而达到数学核心素养落地生根的目的.
数学的大厦不是一天建成的,数学知识的生成是有迹可寻的. 在课堂教学中,要让学生感受到:数学不是高不可攀、与生俱来的,是与人类生活和社会发展紧密相连的. 可以通过运用基础知识、基本技能、基本思想进行探究,在探究的经历中获得基本活动经验,在活动经验基础上提升自己的数学素养.
参考文献:
[1] 单墫. 高中数学教学参考书(数学4)[M]. 南京:江苏教育出版社,2012.
[2] 程仕然,蒋智东. 苏教版《普通高中课程标准实验教科书(必修)数学》中核心概念认知情况的调查报告[J]. 数学教学通讯,2019(15).
