STEM项目研究中的数学作用
2020-01-18刘苏娟
刘苏娟

[摘 要] STEM是推进学校变革、转变学习方式、提升学生综合素质的新生力量. 以人教A版高中数学选修2-1“圆锥曲线”为蓝本,从74个学生的创意中遴选了15个项目,采取文献检索、问卷调查、数据分析、电脑模拟、模型制作等方式,开展了一次“自下而上”的STEM研究. 从中发现,数学之于STEM的作用表现为:以数学知识考证实验猜想、以数学思维寻找创意空间、以数学方法汇通学科融合、以数学语言开展理性协商、以数学思想引领研究进程.建议:STEM研究中习得的方法能有机地回归到学校学习之中.
[关键词] STEM;数学作用;学习方式;综合素质
“STEM”是科学(Science)、技术(Technology)、工程(Engineering)、数学(Mathematics)的简称,旨在以同一主题为引领,打破学科界限,促进跨学科知识的综合运用. 2017年版普通高中课程改革方案强调“普通高中的培养目标是进一步提升学生的综合素质,着力发展核心素养”. 可以预见,随着科技的快速发展和课改的持续深化,STEM将成为推进学校变革、转变学习方式的新生力量.
一个明显的佐证是,“数学建模”在2017年版《普通高中数学课程标准》中占据了前所未有的分量. 当然,建模只是数学应用的美丽一瞥,华罗庚指出:“宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日月之繁,无处不用到数学.”2019年11月,笔者在完成人教A版高中数学选修2-1“圆锥曲线”之后,以本章教材“阅读与思考”为蓝本,带领学生开展了一次“圆锥曲线的光学性质及其应用”的STEM研究. 从首次收集的74个学生的创意中遴选了15个项目,并成立了相应的研究小组. 邀请高校学者、教研专家担任活动顾问,知名高校在读的学长、已从业的学长担任学科顾问,家长、企业主担任社会调研顾问. 采取文献检索、问卷调查、数据分析、电脑模拟、模型制作等方式,历时6个月,让学生体验了一次STEM研究过程. 回顾这一历程,发现数学的作用在STEM中得到了更为生动的体现,远超笔者的预期.
■以数学知识考证实验猜想
数学知识在科学研究中发挥着重要的基础性、工具性作用. 数学知识因其可靠性被大量运用于已有方案的计算、求解等. STEM研究中的问题与平时学生接触到的问题有很大的不同:多数问题没有现成答案,有时还充斥着大量的猜想与失误. 为了让学生体验这种感觉,笔者将生活中常见的台球桌进行了改良,制作了一个微型的椭圆形台球桌,并在球桌内放置了两个玻璃圆片A,B(如图1),设计了一个游戏:师生各自摆放A,B圆片,弹动圆片A,经过椭圆壁反弹后击中圆片B者获胜.
学生跃跃欲试,参与者有很多但命中率很低. 教师摆好圆片后闭上眼睛弹动圆片A,结果百发百中. 胜负悬殊激发了学生的好奇心,于是有了以下对话:
师:老师是否练就了弹指神功?
生1:我观察到老师放置两个小圆片的位置总是固定的,會不会是放在焦点的位置?
师:如果是放在焦点的位置,为什么小圆片经过椭圆壁的反弹就一定会击中另一个圆片?
生1:这好像与物理的入射、反射光线相似,反射镜面也许经过小圆片与椭圆壁碰到那个点的切线,光线从一个焦点出发,经过椭圆壁反射,必定经过另一个焦点.
师:如何验证你的猜想?
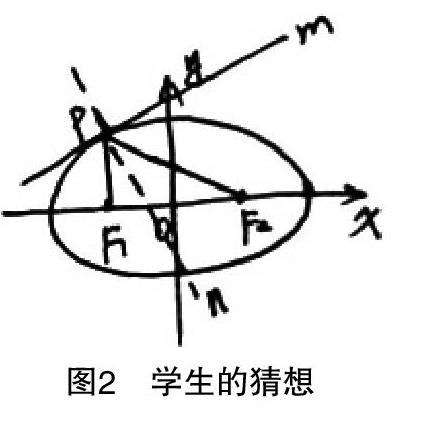
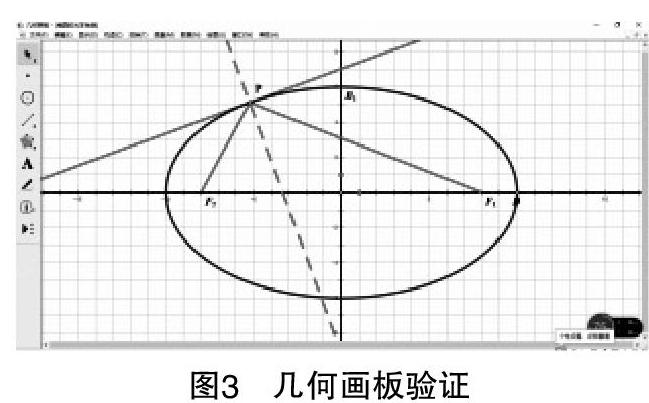
生1:可以用几何画板验证. 如图2,P是椭圆上任意一点,在P点作椭圆的切线m,过点P作直线m的垂线n,连接PF1为入射光线,观察PF1关于直线m对称的反射光线是否经过F2这个点. 如果经过,那说明我们的猜想应该是正确的. (教师根据学生描述的步骤用几何画板验证猜想,如图3)
师:用几何画板验证后,PF1关于m对称的直线好像过点F2,但这样能断定我们的猜想正确吗?
生2:未必!这里可能有误差,需要用代数方法进行计算才能准确证明我们的猜想. 先设点P的坐标,求切线m、垂线n、入射光线PF1以及PF1关于n对称的直线l的方程,判断点F2是否在直线l上.?摇
学生从现实情境中抽象出物理模型,再抽象出数学问题,通过数学问题的解决,得到现实情境的结论,这是数学建模的常见步骤.但在本案中,学生先以“形”初步验证,再利用“切线方程”“点在线上”等解析几何知识,用“数”做出进一步考证,使得数学知识完全地融入猜想的检验、结论的证明之中. 这表明,在STEM研究中,“M”之于“STE”并非简单地提供数学公式、数学定理,还能为“STE”的探索提供可靠的保证,促进“STE”认知领域的扩充.“M”与“S”“T”“E”之间存在着动态的、多向的循环关系(如图4).
■以数学思维寻找创意空间
学生在STEM项目中早期设计的产品大都源于生活经验,一些他们自以为“创新”设计的产品经由网络搜索却已有类似的, 受此挑战,学生亟须寻找新的研究方向. 此时,一些头脑“活络”的学生往往能产生较多创意,笔者发现这种“活络”主要体现在思维品质上,以“纽扣式蓝牙无线助眠耳机”为例.
学生最初试图将抛物线光学性质用于耳机声音的传播,为求最广泛地获得该项目的研究方向,全体成员在“思考——合作——分享”的活动中开展发散思维. 每位学生都写出了从耳机联想到的概念,最后汇集成一个多达五六十个概念的讨论单. 通过系统思维对这些要素进行梳理、分类,剔除了其中过于细枝末节的部分,以及学生觉得他们的能力范围内难以解决的问题,再对余下的概念进行归类、集中,遴选出了“音质效果”“使用体验”“时尚外观”三个类别.
小组成员从自己对现有耳机的需求出发,又选择了“时尚外观”作为主要的研究方向;再次对外观从“炫”“酷”进行选择,最后确定以“酷”为主题,即让耳机随着音乐的节奏而发光. 但搜索网络后发现已有类似的产品,并且用户的使用评价比较满意,学生的早期设计遭遇了瓶颈.
但学生并没有放弃,采用问卷调查、文献检索等方式,集思广益,了解到市场目前的主流需求倾向于格式塔式、骨传导技术设计的耳机. 其中格式塔式耳机——一款通过对外观的时尚设计突出个性,为特殊消费群体“量身定做”的蓝牙耳机;骨传导技术耳机——声音通过颅骨传到内耳,即使以较低的分贝也能实现声音的清晰还原,以避免影响到周围人群. 小组成员通过比较和讨论,他们对骨传导技术产生了极大的兴趣. 紧接着小组成员集中讨论骨传导技术,提出了一个大胆的逆向思考:既然这种耳机可以做到低分贝输入、高分贝输出,根据声音的可逆性,如果可以设计出高分贝输入、低分贝输出的耳机,那么可有效地避免周围人群的打扰. 这一思路立刻引起了大家共鸣. 有学生举例,有时学校的寝室内呼噜声对室友的睡眠干扰较大. 如果把该产品的设计定位于在校学生,那么市场前景将会广阔. 由此确定项目为“纽扣式蓝牙无线助眠耳机”,形成表征(如图5). 以上过程可归纳为图6.
在学生探讨的过程中,貌似没有数学,但始终运用了数学思维. 其中,在思维方式上运用较多的是发散思维和集中思维,发散思维有助于寻找创新源泉,集中思维是为了确定研究方向. 同时在集中、发散的过程中,选择性、批判性的思维品质也开始显露出来. “思维以场的形式存在,通过复杂的中介和不同的方式进行信息加工,以获得关于客观事物的特性、联系和关系的知识.”[1]发现新事物、揭示新规律、发明新技术,“数学从中起到了推动创新性工作的巨大力量”[2].
■以数学方法汇通学科融合
STEM项目研究中的各个环节是多个学科融合的过程,并非“往汤里多加几味调料”. 只有将各学科知识连贯起来进行综合,才能对问题形成系统认识.其中,数学方法是连接不同知识领域的通道,是学科交汇形成的重要阵地.
例如,“抛物线竞技模型组装套材”项目. 这是一组利用电磁能组装的竞技游戏模型,通过抛物面凸透镜的设计,以提高模型中炮弹的命中率. 模型试验初期,项目所需的部分零件通过网购得到,炮弹射击误差较大.
为了解决这个问题,学生从工程视角,用分析法将炮弹精准度问题进行了分解,发现它与数学中的焦点位置、曲面形状、炮弹发射的傾斜度有关. 如何改变这个问题,他们请教了物理老师,得知与物理中的折射系数、透光性、初速度、加速度、动力等相关. 学生试图通过具体的实验操作来检验各个不同数据下的实验结果,但在材料问题上就遇到了困难:有的价格昂贵,有的没有成品而需要定制,还有的无法在短时间内购齐,甚至在参数变换的情况下需要投入大量的实验时间. 为了突破这些囿限,学生转而回到数学:能否通过数学建模的方法设计程序利用电脑仿真模拟实验?例如,通过改变曲面方程,模拟比对椭圆面、抛物面、球面等曲面形状的聚焦效果. 为了找到较为合适的软件,他们又请教了苏州大学光学博士的学长,发现可以在仿真软件Comsol的Optics和Radio Frequency的模块上运行. “数学建模+计算机软件Comsol”为本组装套材的精确度调校找到了一个成本少但运行高效的技术支撑,大大提振了小组成员的研发信心.
在软件运行过程中,还需输入一些参数,如相对介电常数、耗散程度,这又与化学材料相关. 他们又去请教了化学老师,理解了一些相关概念,再回到数学,丰富数学模型中的实验参数进行模拟比对,得到了符合这个游戏套材的理想参数. 经过多次实验、建模,学生获得了各种模具的理想参数.
为了打印模具,他们又去请教了通用技术老师,发现只要有尺寸数据,可根据模具的化学材料选择CNC加工或3D打印来获得模型.为了准确地表达项目的设计,学生采取了数学中的坐标法、图像法,用计算机中的犀牛软件制作成了带有参数的设计图纸. 事实上,在项目研究过程中,学生还参考了若干的外文资料,自学了不少的英文单词;在项目书的撰写过程中,还请教了语文老师.
从这些过程中,我们发现,无论从产品最初的确定还是到材料制作,乃至一个项目书的形成,几乎都是从数学到友邻学科,又从友邻学科回到数学的过程. 这个过程多次循环往复,期间还涉及了心理学、生物学、人体工程学,他们的关系如图7所示. 正如冯纽曼所说:“数学方法渗透并支配着一切自然科学的理论分支,它愈来愈成为衡量科学成就的主要标志.”
在学生上交的74份设计图中,虽然涉及了各友邻学科,但我们几乎可以看到数学方法不仅发挥了学科融合的作用,还延伸至了建筑、工业、军事等多个领域,其中较为典型的设计如表1所示.
■以数学语言开展理性协商
STEM教育以小组合作模式进行,学生在解决项目课题的过程中,团队内部经常需要进行头脑风暴. 一个研究项目在确定主题之前往往需要在多个方案中择优实施,学生在商讨过程中难免各执己见. 这不仅拖慢了研究进度,而且影响到了团队的关系. 理性协商成了凝聚团队向心力、提高沟通效率的重要保障,此时数学语言提供了理性表达的工具.
例如,“神奇的锅”,如图8,学生甲先以立体几何中的直观图描述了产品的整体外观;再用三视图说明了产品的抛物面结构;之后将正视图、侧视图、俯视图放入坐标系中,利用解析几何的坐标法给出了相应尺寸,借鉴Excel中的图表描绘方式,以不同颜色区分不同数据;又用轴截面的光线二维图阐明了设计原理:该产品通过抛物线造型,使太阳光汇聚到焦点,以提供点火、充电等能量,或把手机置于焦点作为扩音器,也可将光源置于焦点形成平行光束,产生舞台追光灯效果.这种借助图形语言描述产品的表达方式瞬间得到了大家的理解和认可.
但是,学生乙从随机数学的角度提出了其中存在的三个矛盾:(1)发热原理高度依赖于阳光,而人们烈日出行的概率反而减少;(2)即使天气晴好,露营地多置于风景秀丽之处,而茂密的植被却又遮挡了阳光;(3)点火项目是最具创意的一项功能,但在携带、使用上远不及防水火柴、打火棒等.
商讨之后数日,学生丙提出了“保暖帐篷”项目,如图9,该项目与甲的方案截然不同. 丙统计了野外生存的必需品,在定义域内罗列了手电筒、点火工具、背包、登山杖、帐篷等物品,进行综合考量之后提出了这一创意. 他也像甲一样用数学语言阐明:(1)原方案的设计原理与能源相关,但发散能源比收集能源更容易做到;(2)根据光线的可逆性,把“太阳光的平行光束汇集到焦点”改为在焦点处放置储电发热管,这样折射出的平行光有助帐篷内温度分布均匀;(3)发热管采用储电功能可以摆脱对天气的依赖.
在此基础上,学生丙又用列表比较的方式,罗列帐篷的缺陷,明确改良的目标,寻找可借鉴的设计、材料,采用映射的“一一对应”进行解决,如图10.
从上面的例子发现,数学语言不仅让一个人的观点能更好地阐述,有力说服他人,还能够在理性协商中发现新的思路与创意. 正如周海中曾言:“数学表达上准确简洁、逻辑上抽象普适、形式上灵活多变,是宇宙交际的理想工具.”
■以数学思想引领研究进程
数形结合、分类讨论、转化思想是高中阶段常见的三种数学思想,在学生解题之中占据着重要的地位,对STEM研究也发挥着重要作用. 笔者发现,一些数学暂差生在STEM研究中对数学思想的应用程度并不比学优生逊色. 而且在大部分的情况之下,这些思想不仅对数学解题水平产生巨大差异,并且还影响着研究的进程和效率.
在STEM项目研究中,数形结合思想运用的较为广泛.例如,“汽车挡光板”项目.某位数学暂差生负责问卷调查,他多次运用数形结合思想,以饼图作为工具来表示产品的满意度,以折线图预测设计关注点的认可度、评估产品未来的市场价值. 在设计环节,沟通和呈现都提倡“用图说话”,用图表达最终设计过程中,需要利用数据集对模型进行验证,才能计算出模型的挡光效果,反复拟合提高挡光强度.
分类讨论思想不仅在资料查找、问卷设计中经常运用,有时还关乎研究进展,甚至项目存亡. 例如,“隧道降噪”,学生在调查现有产品时,最初只单一地查询某寶,发现没有类似产品之后,即着手研究. 然而在完成设计图时,却在中国知网发现了已有类似专利,只能中断. 若在早期调查时就能把大众化网站和专业性网站纳入分类检索对象,就可以避免这一现象发生. 分类讨论不仅可以拓宽学生的思维和视野,还能让他们发现差异,找到新的研究方向. 例如,该项目后来演化为了路边消音板.
转化思想可以使“STE”转化为数学问题,还能在产品研究中出现瓶颈时转变思路. 例如,可折叠的“篮球训练机”项目. 该项目通过篮球架底部为抛物线曲面的设计,解决了训练时费时费力捡球的麻烦,折叠成拉杆箱的设计方便移动篮球架到任何场所搭建训练场. 前期利用软件模拟,评估得知这款篮球架的稳定性远远不够,难以承受篮球投篮带来的压力. 学生试图改变篮球架的抓地力、折叠连接点的牢固性,但无功而返.于是学生把提高承受力转化为减少压力,采取了以下转化:(1)使用人群从任何年龄段改为3~6岁儿童;(2)篮球从直径为24.6 cm的专业篮球改成直径为12 cm的儿童篮球——拍拍球;(3)可折叠设计的目的从方便搭建训练场改为提供组装乐趣以培养儿童的动手能力. 适用人群、设计突破口方向的转变,是对前期研究价值的肯定,同时大大降低了设计难度.
■反思
首先,STEM项目的研究本身就是一个综合提高学生核心素养的过程. 作为数学教育的研究,我们固然需要从不同角度看待数学中的语言、知识、方法、思维、思想等对研究所产生的相应影响;但作为STEM项目的研究,它本身是一个综合的过程,也正因为如此,使得我们在STEM项目研究的过程中,能够自觉地面对学生整体的核心素养,这对于当前教育改革具有重要的启发意义.
其次,在STEM研究中,不能把项目到达产品制造终端作为研究是否成功的评价标准. 高中生尚处于在校学习阶段,最重要的是让学生体验其过程. “学生一旦进行了创造性思考,便说明他们已经充分参与到了学习当中. 学生参与度的提升往往会形成更深层次的学习.”[3]
再次,就数学教学而言,STEM研究最终需回归到数学学习之中. 改变学生的学习方式、数学观念,以更好地促进他们的可持续发展.因此,在STEM过程中所得到的研究问题的方法,我们要把STEM研究中习得的方法引渡回到数学学习之中,为数学探究提供丰富的体验.
参考文献:
[1] 任樟辉. 数学思维理论:学科现代教育理论书系·数学[M]. 广西:广西教育出版社,1998.
[2] 莫里斯·克莱因.古今数学思想(第二册)[M]. 上海:上海科学技术出版社,2002.
[3] 约翰·斯宾塞,A.J.朱利安尼.如何用设计思维创意教学:风靡全球的创造力培养方法[M]. 北京:中国青年出版社,2018.
