高中数学探究式教学的实践研究
2020-01-18王光华
王光华
[摘 要] 新课改风向标下,高中数学课堂教学更加关注学生探究能力和创新精神的培育. 探究式教学作为数学课堂中一种重要的教学方式,教师需依照学情展开研究式教学,引领学生探究知识形成的过程,探究数学概念,探究数学规律,助力学生的数学学习.
[关键词] 探究性教学;数学概念;数学规律;本质
探究即探索,它是数学课堂中一种重要的教学方式. 数学探究就是以问题的解决为目标,以探究性问题为载体,以思考、讨论、互动、自主、评价等活动方式为主线的一种学习活动. 而本文中所指的探究式教学特指的是一种课堂的教学方式,也是建构主义学习理论的一种教学实践模式. 对比传统教学模式,探究性教学更具有实践性和开放性,利于学生的自主探究和学习. 下面笔者结合几个教学片段,谈谈探究式教学的几种类型,为学生的数学学习助力. ?摇
■探究知识形成过程
数学教学的过程不应仅仅是知识的汇聚或是方法的获取,更需要的是对知识形成过程的探究. 基于此,学生的探究性学习品质自然需孕育在探究知识的形成过程中. 然而纵观大量的课堂教学实践,大部分学生还是习惯于“听讲”模式,缺乏數学探究的方法,而知识的建构又是建立在自身的感悟和反思之上的. 因此,教师需要通过“探究式教学”为前提和基础,充分暴露自身的思维过程,进行探究示范,展示知识的形成和发展,使学生在耳濡目染中学会探究的策略与方法,获得丰富的探究体验,进一步地让学生体会概念、公式、法则等结论的来龙去脉,探清知识本质,从而水到渠成地进行自我建构.
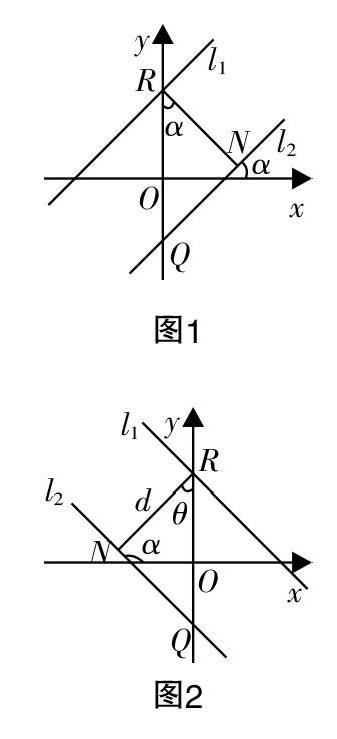
案例1:以“点到直线的距离公式”的探究为例
问题1:已知l■:y=kx+b■,l■:y=kx+b,且有l■∥l■,试求出l■,l■的距离d.
分析:画出图1和图2,即可求出d=RQ·cos(π-α)=■.
问题2:“两平行线间的距离公式”该如何向“点到直线的距离公式”转化?
分析:由平行线间距离处处相等的原理,可在l■上任意取P(x■,y■),则有y■=kx■+b■,可得b■=y■-kx■,代入公式后可得d=■.
问题3:已知直线y=kx+b,点P(x■,y■),试求出点P到l的距离.
分析:只需将问题2中的b■转化为b即可,则有d=■.
问题4:已知直线Ax+By+C=0,点P(x■,y■),试求出点P到l的距离.
分析:令k=-■,b=-■,再代入公式后进行整理,可得d=■. (注:当B=0时,公式同样成立)
说明:本课内容的学习是该章节的重难点之一. 教材中是直接抛出了问题4,以引导学生的分析与求证. 当然以此展开的探究在知识和方法上也是一目了然的,但违背了学生的知识建构的过程,易造成学生学习中知识点的困惑,甚至于偏差. 以上案例中,教师精心设置了一个“问题链”来重组教材内容,使其更具有探索性和层次性;同时教师探究示范“问题1”,为学生的探究铺路引航,逐渐将他们的探究引入深处,让他们进行自主活动、发现和探究问题,经历过程,建立起自己的探究经验,探清其本质,完善学习结构.
■探究数学概念
在知识应用的层面上来看,数学概念是其典型标志,因此,在概念教学的过程中,教师需设计科学而合理的题组,并给予学生充足的时间和空间,让学生尝试和探索,探清概念的内涵,在尝试中获得新知,在探索中获得感悟,学会一种良好的学习方式. 这样一来,概念的得来是在学生的参与中获得的,让学生有了充分的体验和感悟.
案例2:以“集合的含义”的探究为例
问题1:请模仿以下的叙述来介绍自己:我们家有爷爷、奶奶、爸爸、妈妈和我,我来自第一中学.
问题2:请班上所有学生按照性别分为两组:一组为A组,一组为B组. 那么,你属于A组还是B组呢?
问题3:请班上所有学生按照毕业于相同初中的学生站在一起,分成不同的组别,并以此进行编号. 那么,你属于其中的哪个组别呢?
问题4:在以上三个问题中,“家庭”“男生”“女生”“学校”等概念均有什么共同点?
说明:通过以上的“问题串”,引领学生的数学思考,让学生去体验和感知,并以自己的语言去表达,在表达的基础上逐步生成概念. 从现实生活中的实例出发,使学生快速理解和认识概念本身;从分组的数学活动开始,让学生在参与和体验之中寓教于乐,愉快而轻松地学习新知;从数学概念的本质展开,让学生参与概念的由来过程,使其探清概念的内涵,为后续的学习打下坚实的基础. 案例充分表明,学生探究起来兴趣盎然并乐此不疲,为统领全课奠定了良好的基础.
■探究数学规律
数学教学中不仅需要让学生掌握知识,而且更应该关注学生认知能力的培养,使其在数学学习中洞悉数学规律,通过探究数学规律来解决实际问题. 对于规律的探索,本身就是发现问题和发展思维的过程,它可以架构知识间的联系,优化已有知识结构,还可以开拓创新,打通学生的思维通道,利于学生的综合发展. 因此,在探究式教学中,教师可以由浅入深地引领学生参与到规律探索中去,帮助其探清解题规律,以此实现思维和能力的共同发展.
案例3:以“对称问题”的探究为例
问题1:已知点P(x■,y■). (1)请结合图像求出其关于原点的对称点的坐标;(2)请结合图像求出其关于x轴的对称点的坐标;(3)请结合图像求出其关于y轴的对称点的坐标;(4)请结合图像求出其关于直线y=x的对称点的坐标;(5)请结合图像求出其关于直线y=-x的对称点的坐标.
分析:可将其分为中心对称和轴对称进行处理,进而得出结论.
问题2:已知点P(x■,y■),试求出其关于A(a,b)的对称点P′(x,y)的坐标.
分析:借助中点坐标公式,即可求得x=2a-x■,y=2b-y■.
