基于媒介齿条的渐开线圆柱蜗杆斜齿轮传动啮合特性分析
2020-01-18陈燕殷国富衡良王玲
陈燕,殷国富,,衡良,王玲
(1.四川大学空天科学与工程学院,四川成都,610065;2.四川大学制造科学与工程学院,四川成都,610065)
渐开线圆柱蜗杆斜齿轮传动是由一个渐开线斜齿圆柱齿轮与一个渐开线圆柱蜗杆啮合形成的轴间角为90°的空间传动。该传动具有大速比、自锁性、易于制造、成本低、齿面精度高、润滑条件较好、对安装误差不敏感等优点,但其点接触特性也使其承载能力有限、传动效率低。因此,主要用于传递小载荷(≤500 W),被广泛应用于汽车天窗、雨刮、摇窗、电动座椅等低噪音、低强度驱动器中。与传统渐开线圆柱蜗杆传动副的区别在于:以一个渐开线斜齿圆柱齿轮代替由渐开螺旋面滚刀展成的蜗轮,传动副也相应由原有的线接触变为了点接触。渐开线圆柱蜗杆斜齿轮传动的传动原理不同于传统渐开线圆柱蜗杆传动副的对偶范成线接触传动原理;同时,由于其蜗杆为少齿数渐开线齿轮,其传动原理和啮合特性也与交错轴斜齿轮传动的不同,因此在啮合几何学分析过程中,无法直接采用平行轴齿轮的平面啮合理论和蜗杆传动的空间包络理论进行研究。国内外学者对渐开线圆柱蜗杆斜齿轮传动进行了大量的基础研究。LITVIN等[1]基于交错轴斜齿轮传动原理,提出了一种渐开线圆柱蜗杆斜齿轮传动设计方法,分析了不同误差对接触区域及传动误差的影响规律,给出了避免边缘接触的修形方法。KOIDE等[2-3]进行了塑料渐开线斜齿轮圆柱蜗杆传动副和塑料渐开线斜齿轮环面蜗杆传动副的强度及疲劳寿命研究,结果表明:塑料渐开线斜齿轮圆柱蜗杆传动副的重合度与传动副啮合侧隙无关,但塑料渐开线斜齿轮环面蜗杆传动副的重合度与啮合侧隙有关,且二者的齿面接触强度及寿命与传动副的啮合侧隙密切相关。KIM等[4]进行了塑料渐开线斜齿轮与金属圆柱蜗杆啮合传动副的应力分析。DONG等[5-7]研究了大速比渐开线圆柱蜗杆斜齿轮传动的几何参数设计与齿面修形,并基于交错轴齿轮传动原理进行了传动副齿面接触分析,讨论了装配误差对接触区域的影响规律,对正交型和非正交型渐开线圆柱蜗杆斜齿轮传动实例进行了计算和验证。彭文捷等[8-12]进行了渐开线圆柱蜗杆斜齿轮传动的精确建模研究、接触有限元分析和传动性能台架试验,提出了通过齿高修形提高传动副承载能力的方法,并证明该传动副的承载能力和传动效率均较低。郝一舒等[13-14]基于交错轴齿轮传动对塑料斜齿轮钢制蜗杆传动副进行了啮合分析和热分析,研究了塑料齿轮齿面的应力场与热力场分布规律。李传闪等[15-16]利用交错轴齿轮传动原理,进行了塑料圆柱蜗杆与金属渐开线斜齿轮传动的啮合原理分析、接触应力及试验研究,结果表明该传动副具有运行平稳和低噪音的特点。在此,本文作者提出渐开线圆柱蜗杆斜齿轮传动啮合特性分析的媒介齿条法,基于媒介齿条和空间包络原理建立传动副的数学模型,构建传动副的接触点、接触椭圆、接触应力、重合度、滑动率等完整的啮合特性分析方法,并通过数值实例与样件试验进行验证。
1 传动副啮合分析媒介齿条法
在渐开线圆柱蜗杆和渐开线斜齿轮的两共轭齿廓之间加入一个假想的齿条,如图1所示。图中,ω1为渐开线圆柱蜗杆绕其轴线的转动角速度;ω2为渐开线斜齿轮绕其轴线的转动角速度;v3为假想齿条沿蜗杆轴向的移动速度。该假想齿条不依附于任何实体,如同一张没有厚度的纸片折叠而成,它的一侧与渐开线圆柱蜗杆齿面啮合,另一侧与渐开线斜齿轮齿面啮合,它与2个齿面之间分别满足共轭关系。由卡姆士定理[16]可知,在抽出假想齿条后,渐开线圆柱蜗杆与渐开线斜齿轮也必然满足共轭关系,即渐开线圆柱蜗杆、假想齿条、渐开线斜齿轮三者两两之间形成等价共轭关系。因此,称这一假想齿条为“媒介齿条”。借助于“媒介齿条”,即可将渐开线圆柱蜗杆与斜齿轮的复杂空间啮合问题转化为相对简单的斜齿轮与媒介齿条啮合、媒介齿条与蜗杆啮合的问题。
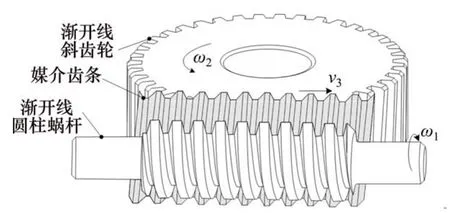
图1 啮合分析媒介齿条法Fig.1 Media rack method for meshing analysis
渐开线圆柱蜗杆与渐开线斜齿轮正确啮合的条件为具有公共的媒介齿条,即:
1)渐开线圆柱蜗杆与斜齿轮的法面模数相等;
2)渐开线圆柱蜗杆导程角等于斜齿轮的螺旋角;
3)渐开线圆柱蜗杆旋向与斜齿轮旋向相同。
2 基于媒介齿条的传动副数学模型
2.1 标架设置
建立渐开线圆柱蜗杆斜齿轮传动副的相关标架如图2所示,图中标架σm(om-xm,ym,zm),σn(on-xn,yn,zn)和σp(op-xp,yp,zp)为空间固定标架,其底矢分别为(im,jm,km),(in,jn,kn)和(ip,jp,kp);onop=b,为渐开线斜齿轮的节圆半径;omon=a,为渐开线圆柱蜗杆斜齿轮传动的实际中心距;运动标架σ1(o1-x1,y1,z1)与渐开线圆柱蜗杆固连,并绕z1轴以角速度ω1旋转,转动角度为φ1;标架σ2(o2-x2,y2,z2)与斜齿轮固连,并绕z2轴以角速度ω2旋转,转动角度为φ2;标架σ3(o3-x3,y3,z3)与媒介齿条固连,并沿媒介齿条基准线方向z3轴以速度v3移动,移动距离为l;标架σ1,σ2和σ3的底矢分别为(i1,j1,k1),(i2,j2,k2)和(i3,j3,k3)。

图2 标架设置Fig.2 Coordinates system setting
由正确啮合运动关系可得各转动参数和移动参数之间的相互关系为

式中:i12=Z2/Z1,Z1为渐开线圆柱蜗杆头数,Z2为斜齿轮齿数。
2.2 媒介齿条齿面方程
媒介齿条齿面在与其固连的坐标系σ3中为一平面,建立媒介齿条相关坐标系如图3所示。图中,标架σ4(o4-x4,y4,z4)和σ5(o5-x5,y5,z5)为与媒介齿条固连的辅助标架,其底矢分别为(i4,j4,k4)和(i5,j5,k5),αn为法面压力角,β为斜齿轮螺旋角,u和v为媒介齿条齿面参数。
经底矢转换和坐标变换,可得媒介齿条齿面在坐标系σ5中的表达式为

媒介齿条齿面单位法矢在坐标系σ5中的表达式为

2.3 渐开线圆柱蜗杆与媒介齿条的啮合关系
依据齿轮啮合原理[16],并通过坐标变换、底矢转换,可得渐开线圆柱蜗杆与媒介齿条啮合过程中的相对速度在坐标系σ5下的表达式为

图3 媒介齿条齿面相关坐标系Fig.3 Coordinates system setting for media rack
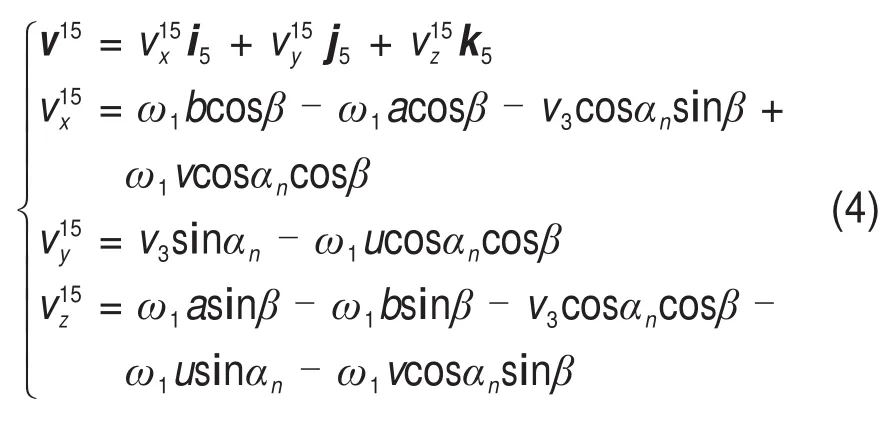
由两共轭齿面既不嵌入也不脱离的正确啮合条件[18],结合式(3)和式(4),有媒介齿条与渐开线圆柱蜗杆之间的啮合函数表达式[17]为

结合式(2)和式(5),有媒介齿条与渐开线圆柱蜗杆之间的接触线在坐标系σ5中的表达式为

结合式(4)和式(6),有渐开线圆柱蜗杆与媒介齿条啮合过程中的一界函数[16]为

结合式(4),(5)和(7),有两共轭曲面的诱导法曲率为
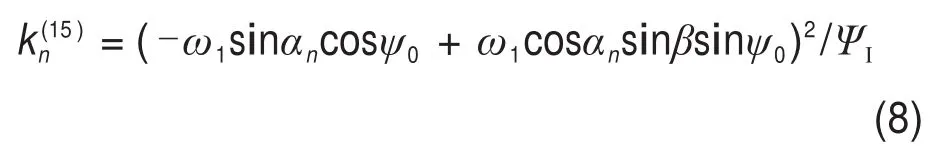
由于媒介齿条齿面为平面,其齿面法曲率为0,因此有渐开线圆柱蜗杆齿面沿任意方向的法曲率为
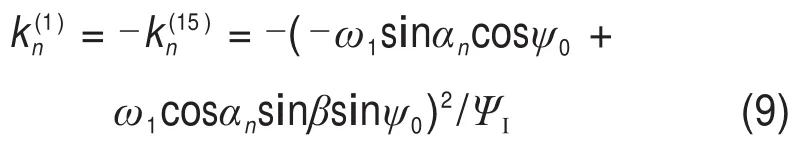
式中:ψ0为所求方向与第一主方向之间的位置夹角。
式(9)中ψ0分别取0°和90°,有渐开线圆柱蜗杆齿面沿i5和j5方向的法曲率分别为:

结合式(4),(5)和(7),有两共轭曲面的诱导短程挠曲率为

由于媒介齿条齿面为平面,其齿面短程挠曲率为0,因此有渐开线圆柱蜗杆齿面沿任意方向的短程挠曲率为

式(13)中ψ0分别取0°和90°,有渐开线圆柱蜗杆齿面沿i5和j5方向的短程挠曲率分别为:

2.4 媒介齿条与渐开线斜齿轮的啮合关系
依据齿轮啮合原理[16],并通过坐标变换、底矢转换,可得媒介齿条与渐开线斜齿轮啮合过程中的相对速度在坐标系σ5下的表达式为

相对角速度转换到与媒介齿条齿面固连的坐标系σ5下的表达式为

由两共轭齿面既不嵌入也不脱离的正确啮合条件[17],结合式(3)和式(16),有媒介齿条与渐开线斜齿轮之间的啮合函数表达式为
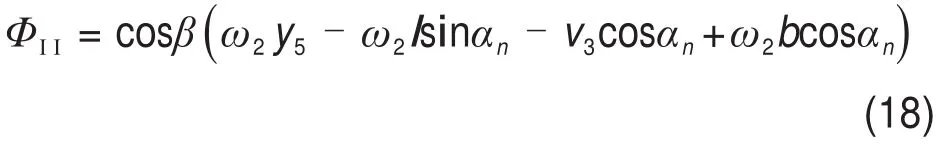
结合式(2)和式(18),有媒介齿条与渐开线斜齿轮之间的接触线在与媒介齿条齿面固连的坐标系σ5中的表达式为
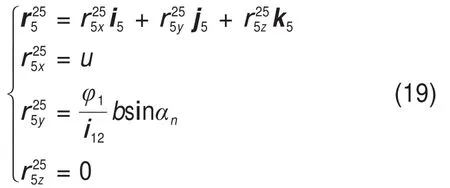
结合式(16)和式(19),有媒介齿条与渐开线斜齿轮啮合过程中的一界函数[17]为

结合式(17),(18)和(20),有两共轭曲面的诱导法曲率为
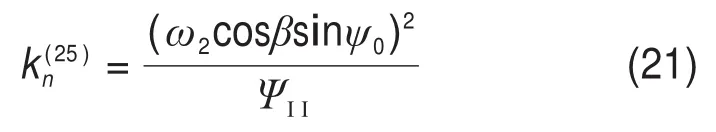
由于媒介齿条齿面为平面,其齿面法曲率为0,因此,有渐开线斜齿轮齿面沿任意方向的法曲率为

式(22)中ψ0分别取0°和90°,有渐开线斜齿轮齿面沿i5和j5方向的法曲率分别为:

结合式(16)和(19),有两共轭曲面的诱导短程挠曲率为

由于媒介齿条齿面为平面,其齿面短程挠曲率为0,因此有渐开线斜齿轮齿面沿任意方向的短程挠曲率为

式(26)中ψ0分别取0°和90°,有渐开线斜齿轮齿面沿i5和j5方向的短程挠曲率分别为:

3 基于媒介齿条的传动副啮合特性
3.1 传动副理论接触点
由接触线方程式(6)可知,渐开线圆柱蜗杆与媒介齿条瞬时呈线接触,如图4(a)中所示的接触线I;由接触线方程式(19)可知,媒介齿条与渐开线斜齿轮瞬时呈线接触,如图4(b)中所示的接触线II。在媒介齿面上,瞬时接触线I与瞬时接触线II的交点,即为渐开线圆柱蜗杆齿面与渐开线斜齿轮齿面啮合的瞬时接触点,如图4(c)所示。
联立式(6)和式(19),可得渐开线圆柱蜗杆齿面与渐开线斜齿轮齿面啮合的瞬时接触点在媒介齿条齿面固连的坐标系σ5中的表达式为

通过坐标变换,可得瞬时接触点在渐开线斜齿轮固连坐标系σ2下的表达式为


图4 瞬时接触关系Fig.4 Instantaneous contact relationship
3.2 传动副实际接触椭圆
渐开线圆柱蜗杆斜齿轮传动副的两共轭齿面之间理论上为点接触,但齿面受载变形后,将在啮合点的切平面内形成瞬时椭圆接触区,如图5所示。

图5 瞬时接触椭圆示意图Fig.5 Instantaneous contact ellipse
基于齿轮啮合原理[17],该瞬时接触椭圆方程在公切面坐标系σ5中的表达式为

式中,δ为理论接触点的弹性变形量,由传动副材料确定;系数A和B由下式确定[16]:
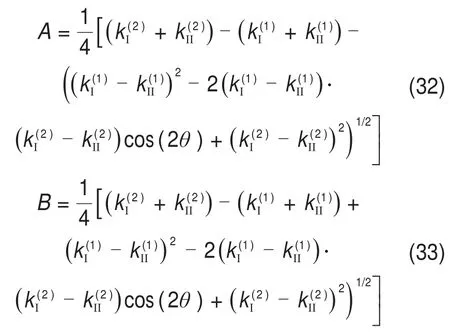
式中,和分别为接触点在渐开线圆柱蜗杆齿面上的最小曲率和最大曲率;和分别为接触点在渐开线斜齿轮齿面上的最小曲率和最大曲率;θ为接触点在两共轭齿面上主方向的夹角。
由式(27)和式(28)可知,瞬时接触点在渐开线斜齿轮齿面沿i5和j5方向的短程挠曲率为0,因此,i5和j5方向为瞬时接触点在该齿面的主方向,其主曲率分别为:
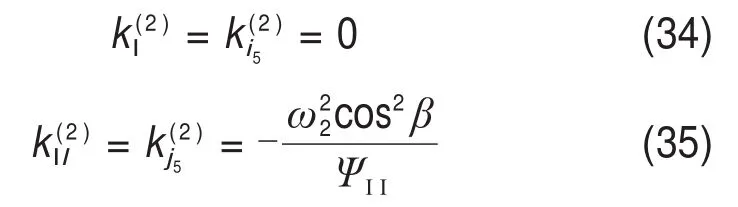
由式(14)和式(15)可知,瞬时接触点在渐开线圆柱蜗杆齿面沿i5和j5方向的短程挠曲率不为0,因此,i5和j5方向不是瞬时接触点在该齿面的主方向,并通过图6所示曲率圆进行求解。
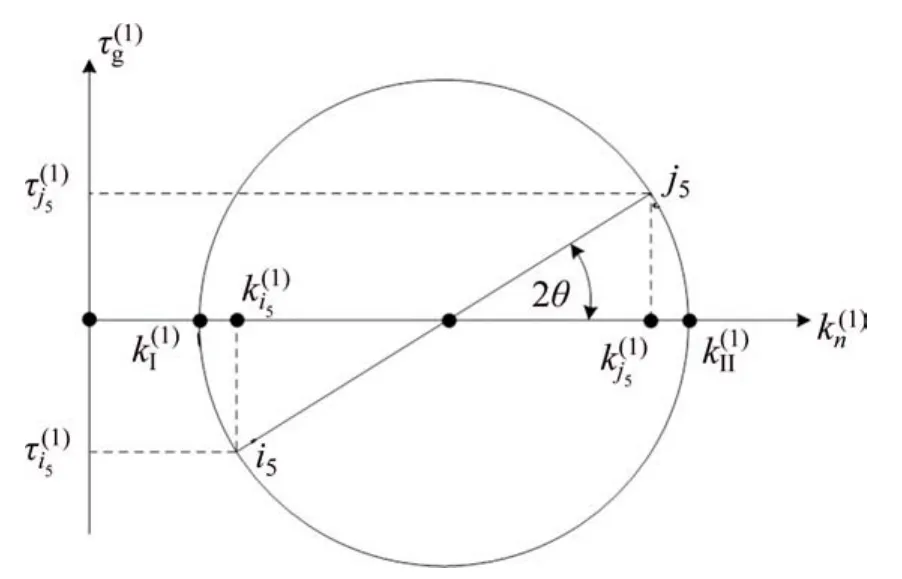
图6 接触点在蜗杆齿面的曲率圆Fig.6 Curvature circle of contact point
结合式(10),(11),(14)和(15),并由图6所示几何关系[17],有:

3.3 传动副的接触应力
通过渐开线圆柱蜗杆斜齿轮传动副共轭齿面间瞬时接触椭圆式(31),结合弹性力学原理,有共轭齿面间的最大接触应力为[18]

式中,P为两共轭齿面间所受的正压力;系数A和B通过式(32)和式(33)确定;μ1和μ2分别为渐开线圆柱蜗杆和斜齿轮材料的泊松比;E1和E2分别为渐开线圆柱蜗杆和斜齿轮材料的弹性模量,λa和λb分别为接触椭圆沿长半轴和短半轴的轴长系数,由瞬时接触椭圆的长半轴与短半轴的长度之比确定。
3.4 传动副的重合度
重合度是传动副实际啮合线长度与单齿啮合线长度的比值,直接影响着传动副的承载能力和振动噪音。渐开线圆柱蜗杆斜齿轮传动属于点接触空间传动,重合度对其性能影响尤为重要。
通过接触线方程式(6)可知,渐开线圆柱蜗杆与媒介齿条共轭的瞬时接触线为一固定斜线,在啮合过程中不发生变化;由接触线方程式(19)可知,媒介齿条与渐开线斜齿轮啮合的瞬时接触线为一变化斜线,在啮合过程中逐渐从齿顶变化至齿根;因此,渐开线圆柱蜗杆斜齿轮传动副的啮合过程如图7所示。图中,瞬时接触线I为渐开线圆柱蜗杆与媒介齿条固定啮合线,瞬时接触线II为媒介齿条与渐开线斜齿轮的变化啮合线;啮入时的瞬时接触线II与固定瞬时接触线I的交点为传动副的啮入点Pin,啮出时的瞬时接触线II与固定瞬时接触线I的交点为传动副的啮入点Pout。
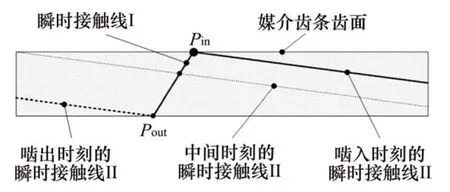
图7 传动副齿面啮合过程Fig.7 Meshing process of transmission pair tooth surface
根据重合度的广义内涵并结合渐开线圆柱蜗杆斜齿轮传动的特点,其重合度ε可表示为

式中,φ1in和φ1out分别为啮入点Pin和啮出点Pout对应的蜗杆转角,并满足以下等式条件:
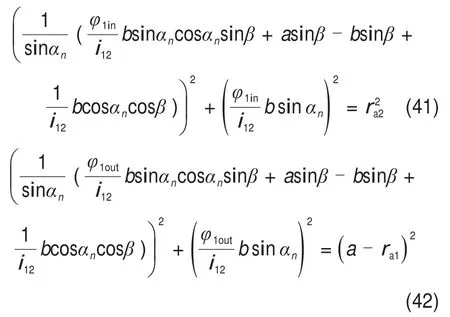
式中,ra1和ra2分别为渐开线圆柱蜗杆和斜齿轮的齿顶圆半径。
4 传动副实例分析
基于上述啮合性能分析方法,以某汽车座椅水平调节器上的渐开线圆柱蜗杆斜齿轮传动副为例,对其展开啮合性能分析。传动副斜齿轮采的基本参数如表1所示。

表1 传动副几何参数Table 1 Geometric parameters of transmission pair
利用MATLAB数值分析软件编制程序,以传动副瞬时接触点在渐开线斜齿轮齿面坐标系中表达式(30)为基础,以渐开线圆柱蜗杆转角为循环变量,取齿面轴向坐标z2为横坐标,取齿面径向坐标为纵坐标,得传动副在渐开线斜齿轮齿面上的接触轨迹点如图8所示;基于传动副共轭齿面微观邻域特征数字和瞬时接触椭圆表达式(31),可得每一瞬时接触点处的接触椭圆长半轴如图8中短实线所示。图8中,每相邻两瞬时接触点之间的蜗杆转角φ1差值为90°。
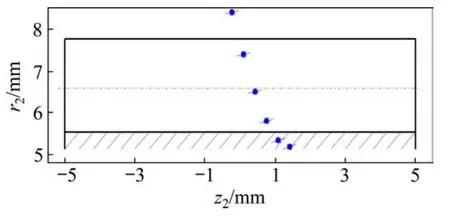
图8 传动副理论接触轨迹Fig.8 Theoretical contact trajectory of transmission pair
建立传动副精确三维实体模型和有限元分析模型,渐开线圆柱蜗杆材料PEEK的弹性模量取3.8×109Pa、泊松比取0.4,斜齿轮材料45号钢的弹性模量2.1×1011Pa、泊松比取0.27,对斜齿轮施加10 N·m扭矩进行静态接触分析,传动副单齿啮合和两齿啮合时的齿面接触状态及接触应力情况如图9所示。从图9可以可见:传动副瞬时接触点位置及接触椭圆长轴方向与图8中数值分析结果一致,单齿接触时共轭齿面间最大接触应力314.6 MPa。
以上述材料属性为基础,利用传动副共轭齿面间的最大接触应力计算式(40),得传动副在单齿啮合时共轭齿面间的最大接触应力为278.5 MPa,与有限元分析结果的相对误差为13%。
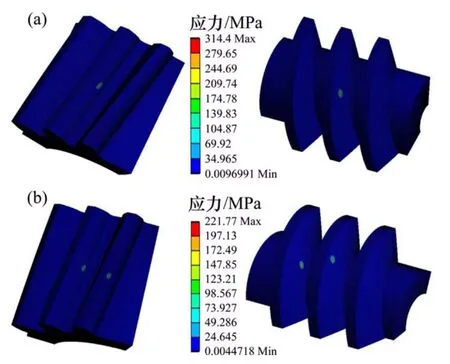
图9 传动副齿面接触状态及应力情况Fig.9 Contact state and contact stress
利用重合度计算公式(41),并结合传动副齿面接触点计算程序,得传动副的重合度ε=1.17。该重合度与图8和图9所示的结果一致。
传动副中渐开线圆柱蜗杆采用注塑成型,渐开线斜齿轮采用滚齿加工,试制样件后装机运行后如图10所示。图10中,渐开线斜齿轮齿面的实际接触痕迹与图8和图9所示的结果完全一致。

图10 传动副实际接触痕迹Fig.10 Actual contact trace of transmission pair
5 结论
1)传动副共轭齿面间呈瞬时理论点接触,由于材料的弹性变形而形成瞬时接触椭圆。
2)传动副接触轨迹在斜齿轮齿面上沿轮齿中部齿高方向倾斜分布,接触椭圆的长轴方向与接触轨迹方向基本保持垂直状态。
3)传动副共轭齿面间的接触应力大,适用于轻载领域。
4)传动副的重合度小,与齿轮传动一致,无法达到蜗杆传动瞬时多齿接触。
